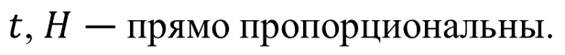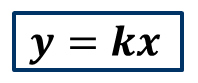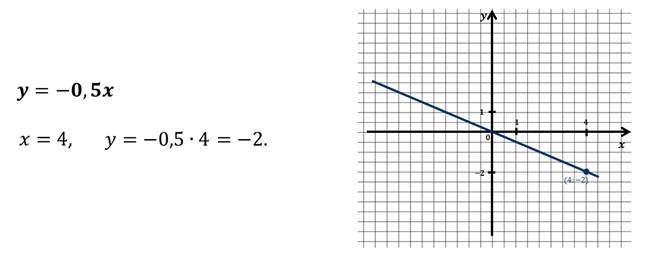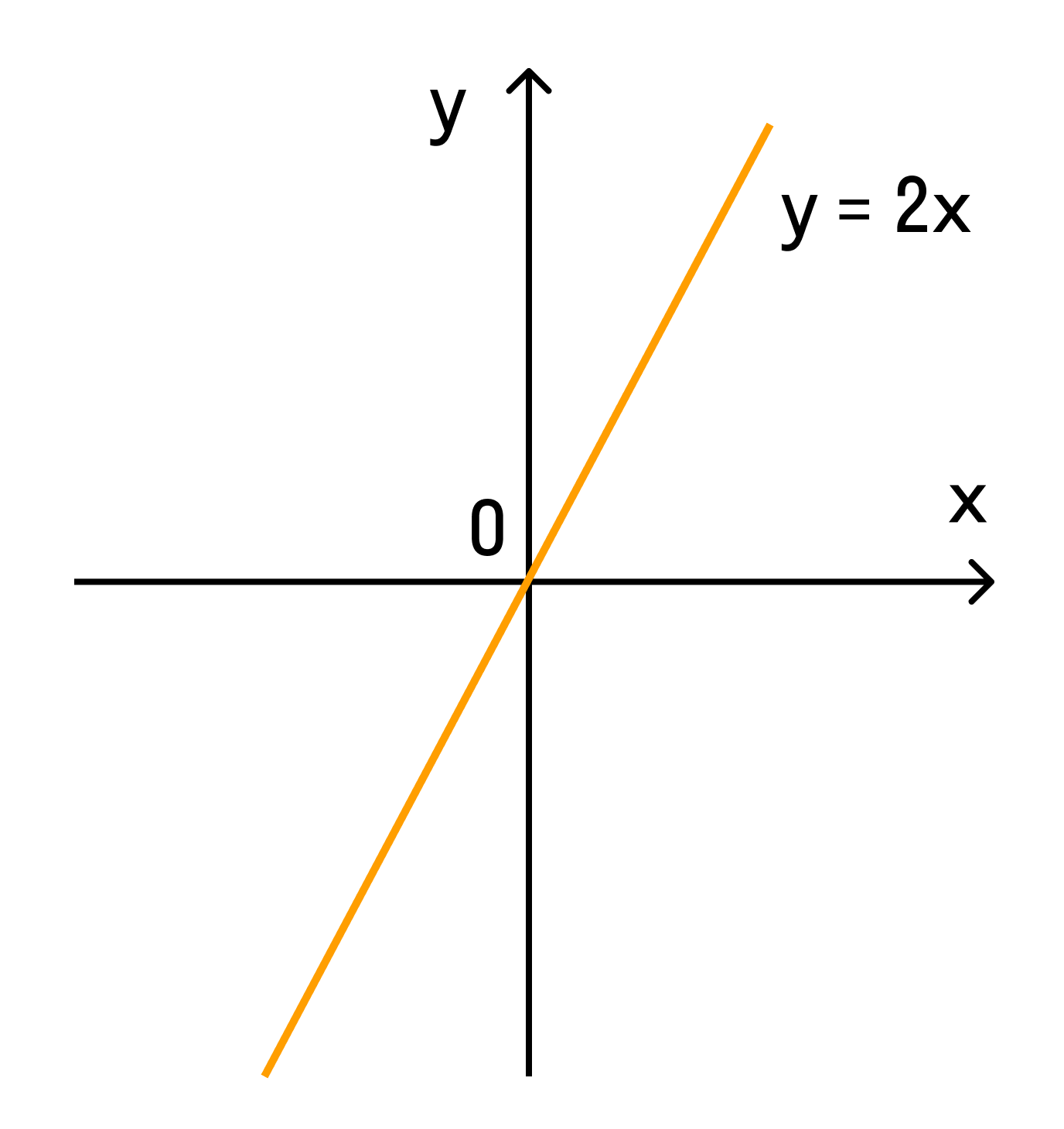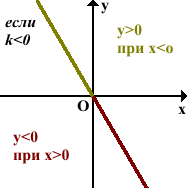что такое график прямой пропорциональности

Прямая пропорциональность и её график

Урок 15. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Прямая пропорциональность и её график»

· ввести понятие «прямая пропорциональность»;

· привести примеры, когда прямая пропорциональность встречается в повседневной жизни;

· построить график прямой пропорциональности;

· определить от чего зависит расположение графика в координатной плоскости.

Давайте рассмотрим пример.

Обратите внимание, что если переменную t увеличить, например, в 2 раза, то и переменная H также увеличится в 2 раза. То есть:

Также заметим, что зависимость высоты растения от времени его роста мы задали формулой вида:

В рассматриваемом примере: k = 2,5, а переменная t является независимой.

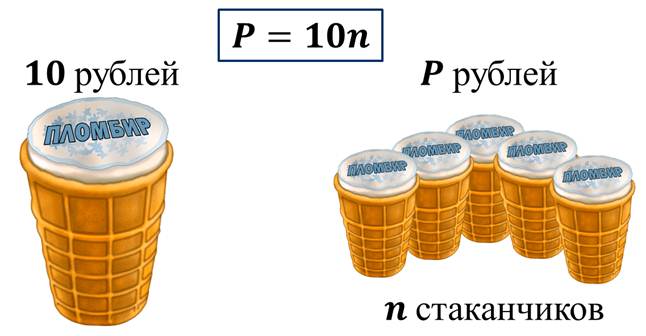
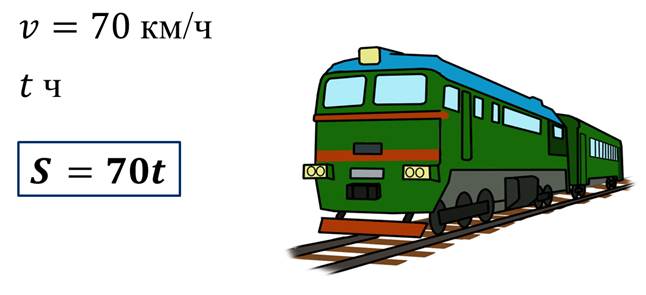
С прямой пропорциональностью мы с вами часто встречаемся в повседневной жизни.

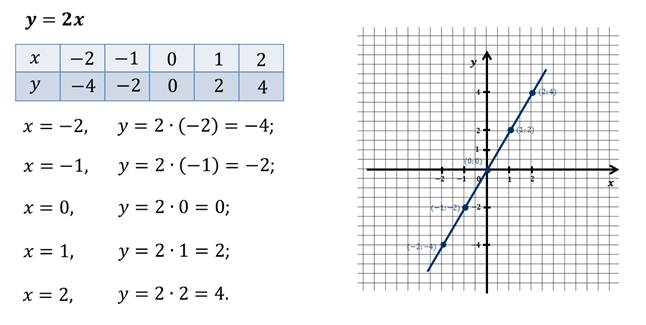
Теперь давайте построим график прямой пропорциональности:

Видим, что все точки лежат на одной прямой, которая проходит через начало координат. Для убедительности можем даже приложить линейку.

Таким образом, можем сформулировать определение.

Графиком прямой пропорциональности y = kx является прямая, проходящая через начало координат.

Нам известно, что прямая определяется двумя точками. А значит, для построения графика функции y = kx достаточно указать любую точку графика этой функции, которая отличается от точки с координатами: (0, 0), то есть от начала координат.

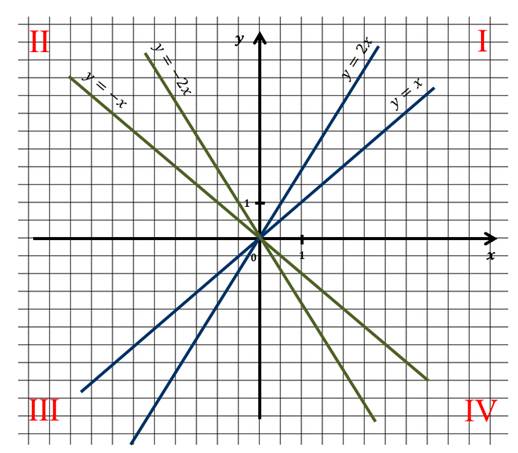
А теперь посмотрите на рисунок, на котором изображены графики прямой пропорциональности.

Обратите внимание, что графики тех функций, которые имеют положительный коэффициент k расположены в первой и третьей координатных четвертях, а которые имеют отрицательный коэффициент k – во второй и четвёртой четвертях. То есть расположение графика функции y = kx в координатной плоскости зависит от коэффициента k.

Источник

Прямая и обратная пропорциональность

Основные определения

Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.

Зависимости также можно классифицировать по формам: функциональная и статистическая.

Функциональная зависимость между двумя переменными величинами характеризуется тем, что каждому значению одной из них соответствует вполне определенное и единственное значение другой.

В математике функциональной зависимостью переменной Y от переменной Х называют зависимость вида y = f(x), где каждому допустимому значению X ставится в соответствие по определенному правилу единственно возможное значение Y.

Статистическая зависимость — это зависимость случайных величин, когда изменение одной переменной приводит к изменению другой.

Если изменение одной из случайных величин влечет изменение среднего другой случайной величины, то статистическую зависимость называют корреляционной. Сами случайные величины, связанные корреляционной зависимостью, оказываются коррелированными.

Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.

Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.

Есть две разновидности пропорциональностей:

Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.

Прямо пропорциональные величины

Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.

Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».

Свойство прямо пропорциональной зависимости:

Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.

Примеры прямо пропорциональной зависимости:

Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.

Формула прямой пропорциональности

y = kx,

где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.

Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.

Формула коэффициента прямой пропорциональности:

Графиком прямо пропорциональной зависимости величин является прямая линия.

Например, при k = 2 график выглядит так:

Пример 1.

В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.

Пример 2.

Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?

Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.

Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.

Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:

Ответ: 20 человек напишут 420 постов за 12 дней.

Обратно пропорциональные величины

Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.

Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».

Свойство обратной пропорциональности величин:

Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.

Примеры обратно пропорциональной зависимости:

Формула обратной пропорциональности

где y и x — это переменные величины,

k — постоянная величина, которую называют коэффициентом обратной пропорциональности.

Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.

Формула коэффициента обратной пропорциональности:

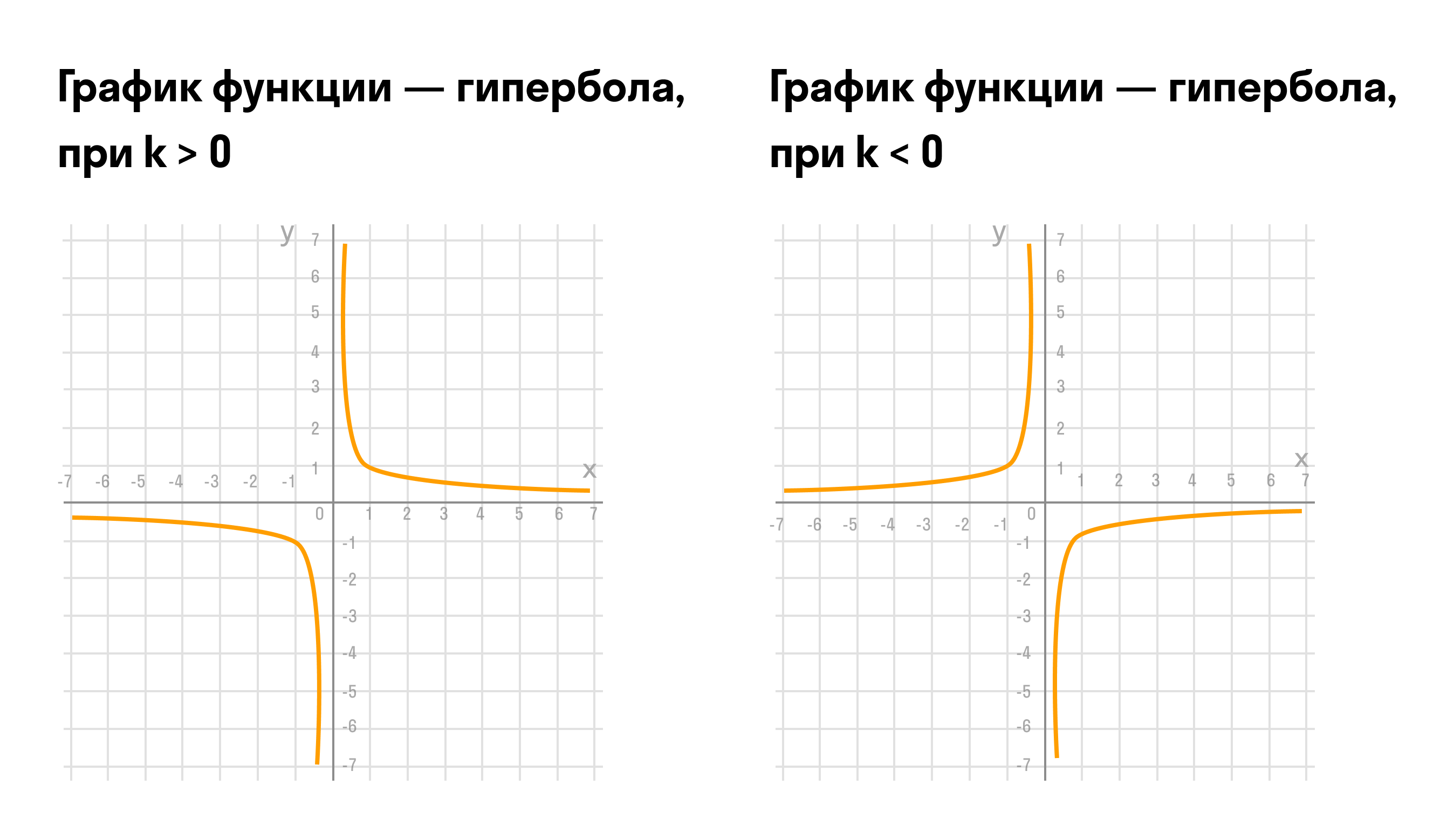
Графиком обратно пропорциональной зависимости величин является гипербола.

Свойства функции обратной пропорциональности:

Потренируемся

Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?

Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?

Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.

Соотношения равны, но перевернуты относительно друг друга.

Источник

Прямая пропорциональность и ее график

В 7 и 8 классе изучается график прямой пропорциональности.

Как построить график прямой пропорциональности?

Рассмотрим на примерах график прямой пропорциональности.

График прямой пропорциональности формула

График прямой пропорциональности представляет функцию прямая пропорциональность.

В общем виде прямая пропорциональность имеет формулу

От величины и знака коэффициента прямой пропорциональности зависит угол наклона графика прямой пропорциональности по отношению к оси икс.

График прямой пропорциональности проходит

График прямой пропорциональности проходит через начало координат.

График прямой пропорциональности есть прямая. Прямая задается двумя точками.

Таким образом при построении графика прямой пропорциональности достаточно определить положение двух точек.

Но одну из них мы всегда знаем – это начало координат.

Осталось найти вторую. Посмотрим пример построения графика прямой пропорциональности.

Постройте график прямой пропорциональности y = 2x

Постройте график прямой пропорциональности, заданной формулой

Берем любое число из области определения прямой пропорциональности, пусть это будет 1.

Найти значение функции при икс равное 1

то есть при x = 1 получаем y = 2. Точка с этими координатами принадлежит графику функции y = 2x.

Мы знаем, что график прямой пропорциональности есть прямая, а прямая задается двумя точками.

Одну из них мы только что нашли, а второй для прямой пропорциональности всегда является начало координат.

Теперь мы готовы построить график функции y = 2x.

Отмечаем на координатной плоскости точку с координатами (1; 2).

Через данную точку и начало координат проводим прямую линию

Мы получили график прямой пропорциональности, заданной формулой y = 2x.

Источник

Функция прямая пропорциональность

Функция вида y=kx, где k — число (k≠0), называется функцией прямой пропорциональности (или функция прямая пропорциональность).

Число k называется коэффициентом пропорциональности. О переменной y говорят, что она пропорциональна переменной x.

Прямая пропорциональность — частный случай линейной функции y=kx+b (при b=0).

Графиком прямой пропорциональности является прямая, проходящая через начало координат — точку O (0;0).

Для построения графика прямой пропорциональности достаточно взять одну точку, вторая — точка O.

Свойства функции прямой пропорциональности

1) Область определения — множество действительных чисел:

2) Область значений — множество действительных чисел:

3) Нуль функции (y=0) при x=0.

4) При k>0 функция y=kx возрастает, при k 0 график функции проходит через I и III координатные четверти.

Функция принимает положительные значения при положительных значениях аргумента:

Функция принимает отрицательные значения при отрицательных значениях аргумента:

Число k называется угловым коэффициентом прямой y=kx.

k=tg α, где α — угол, который прямая образует с положительным направлением оси Ox.

Чтобы сравнить угловые коэффициенты прямых, сравниваем углы между прямыми и положительным направлением оси абсцисс.

Источник

Прямая и обратная пропорциональность — формулы, свойства и графики функций

Одно из основных понятий курса математики в 6 классе – это прямая и обратная пропорциональность. Если некоторая величина (время, масса, цена) изменяется, и одновременно другая величина (расстояние, объем, затраты) тоже меняется, то величины находятся в зависимости между собой, то есть пропорциональны друг другу.

Взаимосвязь между величинами не всегда означает наличие пропорциональности. Так, высота дерева растет с его возрастом, но не во столько же раз. Составление пропорций помогает решить многие задачи как в математике, так и на практике.

Прямая пропорциональность

Если при изменении одного параметра другой изменяется таким же образом, то эти величины прямо пропорциональны друг другу. В этой пропорции увеличение расстояния вдвое означает увеличение времени также двукратно.

Например, при движении автомобиля с постоянной скоростью, время, затраченное на преодоление расстояния, будет прямо пропорционально этому расстоянию. То есть, если 50 км автомобиль проедет за 1 час, то 100 км с той же скоростью он преодолеет за 2 часа.

Функция прямой пропорциональности и ее график

Эта зависимость описывается следующей формулой:

Здесь k и называется коэффициентом пропорциональности.

Графически функция изображается прямой, которая пройдет через начальную точку координат. Строят график следующим образом: находят одну точку, затем чертят прямую через эту точку и начало координат.

Пример построения

Нужно построить график у = 3х. Подставляем вместо х единицу, вычисляем y = 3, то есть находим координаты (1; 3). Отмечаем эту точку на координатной плоскости, проводим прямую линию через нее и точку (0; 0).

Вот так будет выглядеть график y = k * x при k > 0 (слева) и при k Свойства функции прямой пропорциональности

Основные свойства следующие:

область определения, значений составляют все действительные числа;

возрастает при всех значениях x, если k > 0;

если коэффициент со знаком «-», т. е. если k 0, то прямая располагается в 1 — 3 координатных четвертях и образует острый угол с осью Х, если k Обратная пропорциональность

Рост одного параметра ведет к уменьшению другого в такое же количество раз, и наоборот, при уменьшении одной величины другая увеличивается во столько же. Это значит, что они обратно пропорциональны друг другу.

Пример: трое рабочих выполнят порученную им работу за 2 часа, а 6 человек такое же задание осилят за 1 час. То есть двукратное увеличение числа работников привело к уменьшению затраченного времени вдвое. Конечно, если прочие факторы неизменны (производительность труда, условия работы).

Функция обратной пропорциональности и ее график

Функция задается формулой:

где k – любое действительное число, кроме 0.

График данной зависимости — это гипербола, ее ветви находятся в 1 и 3 четвертях системы координат при k > 0, или во 2 и 4, если коэффициент меньше 0. Ветви гиперболы симметричны относительно точки (0; 0).

Строят график так: нужно задать значения х, затем вычислить значения у, результаты оформить в виде таблицы. Верхняя строка таблицы заполняется значениями х, нижняя — y.

Пример построения

Нужно построить график функции y = 8/x.

Вот так выглядит таблица для данной функции:

Полученные точки отмечают на координатной плоскости, затем соединяют плавной линией. График будет выглядеть так:

Свойства функции обратной пропорциональности

области определения, значений функции D(y) – это все действительные числа, кроме 0, т. е. D(y):= x ≠ 0;

если коэффициент больше 0, функция является убывающей для всех x; если меньше 0, то y увеличивается для любых значений x;

оси координат 0х и 0у — это асимптоты по отношению к ветвям гиперболы, которые приближаются к ним, но не достигают их.

К составлению математических пропорций во многих случаях сводится решение самых разнообразных задач. Например, покупая 1 булочку по определенной цене, подсчитывают затраты на 4 булочки – получается в 4 раза больше.

Ускоряют шаг при ходьбе в 2 раза – достигнут цели вдвое быстрее. Вводят второго кассира в магазине – убывает очередь вдвое. Во всех этих случаях и им подобным применима теория о прямой и обратной пропорциональности.

Источник