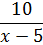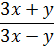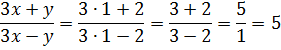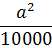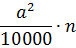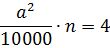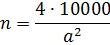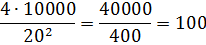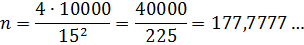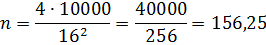Что в алгебре подразумевается под буквами
Знакомимся с алгеброй!
Ну что, дорогие товарищи! Могу вас поздравить! Мы с вами медленно, но верно взрослеем! И математика, с которой мы с вами будем работать, тоже потихоньку будет становиться серьёзнее, да.)
В чём же будет заключаться наше взросление? А взросление будет заключаться вот в чём.
Все мы с начальной школы уже попривыкли работать с числами. Складывать/вычитать, умножать/делить числа. Самые разные — целые и дробные, положительные и отрицательные. Но! Жизнь — штука многогранная! И преподносит много сюрпризов. И вот один из них.
В жизни очень часто приходится работать с различными числовыми величинами не в конкретном, а в общем виде. Это может быть время, расстояние, температура, цена, скорость — совершенно любая числовая величина. Т.е. величина, которую как-то можно выразить числом (секунд, дециметров, рублей, километров в час и так далее). Взаимоотношения между величинами задаются в математике, чаще всего, формулами. Прямо в общем виде. Или уравнениями. Вспомните хотя бы простенькие задачки на движение, для решения которых используется ключевая формула:
S = V·t
S — пройденный путь,
V — скорость движения,
К сожалению, для работы с числовыми величинами в общем виде, одних только чисел (т.е. набора циферок) уже недостаточно. Требуются ещё и буквы. Которые как раз и характеризуют нужную нам величину в общем виде. Стало быть, для работы с общей (буквенной) записью числовых величин (т.е. формулами и уравнениями) нужна своя математика. И она есть! Как только к чиселкам в употребление добавляются ещё и буковки, то привычная нам арифметика превращается в… Превращается в… грамматику?) Не-а! Не угадали.) В алгебру! Красивое и мощное слово.)
Естественно, в новом разделе математики (алгебре) возникают свои правила и свои порядки. Некоторые вещи будут хорошо знакомы вам из арифметики (сложение/вычитание, умножение/деление, сокращение дробей, возведение в степень и т.д.), но некоторые будут и непривычными. Почему? А потому, что новыми! А любая новизна всегда предполагает некоторый период привыкания, да.) Вот и мы освоимся и попривыкнем.
Что изучает алгебра? Как работает алгебра?
Итак, предмет алгебры. Что же изучает алгебра?
Фактически, алгебра — это просто обобщение изучения арифметики. Ни больше, ни меньше.
Итак, удивляемся, но запоминаем. Буквы в алгебре — это, фактически, те же самые числа! Только числа эти замаскированные. Или подразумевающиеся. И поэтому носят особое название — переменные величины. Или кратко — переменные.
Почему — переменные? А потому, что под любой буквой в алгебре всегда скрывается какое-то число. И любую букву при желании можно заменять на какое-то число. Совершенно любое (какое допустимо, конечно). Об этом в первом уроке про числовые и алгебраические выражения немного говорилось. Но и тут не грех вспомнить будет.)
Например, возьмём конкретное алгебраическое выражение. Пусть а+1. В нём есть единичка (число 1), которая вопросов обычно ни у кого не вызывает. Единичка и в Африке единичка. И ещё есть буковка «а». А вот тут уже у многих появляются вопросы, да… Что это за буква такая? Что она означает и зачем вообще написана?
Ответ: буковка «а» – это и есть та самая переменная величина.
Между прочим, простенькие алгебраические выражения очень легко и просто расшифровываются словесно. Да-да! Великий и могучий русский язык способен очень на многое. В том числе и в математике, да.
Например, словесная расшифровка нашего злого выражения а+1 будет при этом гласить: к любому числу (а) прибавить единичку (1).
Обратите внимание на слова — именно «любому числу» (а не букве!). Не можем мы складывать буквы с числами «в лоб». Как и не можем складывать метры с килограммами, да…
Запоминаем:
Буквы в алгебре — это просто символы! Под которыми скрываются различные числа. И не более того. Буквы можно заменять на различные числа.
Потренируемся теперь в словесной расшифровке более сложных алгебраических выражений. Возьмём другое выражение. Посложнее. Например:
Так прямо по-русски и читаем: десятку (10) поделить на разность любого числа (х) и пятёрки (5).
Конечно, здесь число икс может быть уже не совсем любым. Про смысл алгебраического выражения помните? И чем же у нас не может быть икс в этом выражении? Правильно, пятёркой не может быть! То есть, числом, при подстановке которого получается запретное действие (в данном случае — деление на ноль).
А как словесно расшифровать выражение, скажем, x+y?
Легко! К любому числу икс (х) прибавить любое число игрек (у).
Или так: сумма любых двух чисел икс (х) и игрек (у).
Да-да! Именно так. Только весь фокус этого алгебраического выражения состоит в том, что под буквами икс и игрек скрываются (подразумеваются), в общем случае, уже разные числа. Именно поэтому используются и разные буквы, да.)
Например, если бы мы твёрдо были уверены, что нам надо сложить два одинаковых числа (например, 1+1 или 5+5), то алгебраически мы бы записали:
А вот если нам надо сложить два разных числа (скажем, 1+2 или 5+7) то для этого другого числа нам и букву другую выбирать приходится, да… Такова суровая жизнь.)
Запоминаем:
В алгебре под одинаковыми буквами подразумеваются одинаковые числа. А под разными буквами — в общем случае, разные числа.
Почему я сделал оговорку «в общем случае»? Потому, что в частном случае — да, под разными буквами могут оказаться и одинаковые числа. При желании.) Скажем, в выражении х+у мы же имеем право взять икс и игрек по единичке? Имеем! Сложим — получится двойка. Возьмём икс и игрек по сотке и сложим — получим двести. И так далее…
Но любой частный случай — лишь часть общего. На то он и частный, да.) А в общем случае, данная запись говорит нам о том, что числа икс и игрек — разные. И буквы — тоже разные.
Понимание сути назначения чисел и букв в алгебре позволяет, как минимум, понимать и решать простейшие задания. Например, такое:
Всё проще простого. Если не понимать смысл назначения буковки b в выражении 2b+3, задание не решить, да… Но мы-то ведь уже в теме, правда?)
Итак, мы знаем, что в алгебраическом выражении 2b+3 под буквой b (или переменной b, что одно и то же) скрывается какое-то число. Какое именно — обычно мы не знаем. Но в нашем задании значение b указано конкретно прямым текстом. Это 0,3. Что надо сделать? Правильно, просто тупо подставить вместо b число 0,3 да и посчитать, что получится:
Это правильный ответ.
Если бы в задании было бы сказано: «… при b = 0″, что бы мы делали? Правильно! Подставляли бы вместо b нолик. И снова считали. Получили бы 3. И так далее. Улавливаете?)
Или другое задание. Покруче.
Имеет ли смысл выражение
И снова перед нами алгебраическое выражение. Ибо помимо конкретного постоянного числа (тройки), в нашем выражении тусуются ещё и буковки. Целых две — икс и игрек. Выражение более сложное. Дробь какая-то… Ну и ладно.) Чтобы справиться с заданием, достаточно самых начальных знаний алгебры. Никаких специальных правил действий с алгебраическими дробями здесь знать не нужно. Совсем.) Об этом в других, более серьёзных уроках, будет.)
Итак, мы в курсе, что под буквами икс и игрек тоже скрываются какие-то числа. Различные числа. Поэтому и буквы в задании — разные.)
В качестве конкретных значений этих различных чисел нам предложены двойка (х) и шестёрка (у).
Вот и подставляем двойку и шестёрку вместо икс и игрек в нашу дробь и смотрим, что получится-то…
Чтобы не наляпать ошибок (оно нам надо?), можно по отдельности сосчитать числитель и знаменатель. Вот и действуем.
Ну ладно. Двенадцать так двенадцать. Так уж получилось…
Хорошо, считаем знаменатель:
Ух ты, какая забавная штука-то… А знаменатель-то нулю оказался равен! На который делить нельзя, да… Надеюсь, вы помните из арифметики, что дробь — это деление? Числителя на знаменатель?)
Вот вам и ответ: нет. Выражение не имеет смысла.
Прошу заметить одну важную вещь: наше выражение не имеет смысла не вообще само по себе, а только при предложенных значениях переменных (x=2 и y=6). При каких-нибудь других значениях букв (скажем, при x=1 и у=2) у нашего выражения смысл появляется:
Почувствуйте разницу, как говорится!
И тут я слышу неосторожный вопрос:
А зачем нужна алгебра? Какие задачи она изучает и решает?
И правда, зачем нам вообще городить весь этот огород с числами и буквами, что-то там подставлять, да ещё и периодически посматривать, считабельно или нет?
Зачем нам вся эта символьная и буквенная схоластика… пардон… алгебра?
Вообще-то, со смысла и назначения алгебры наш урок и начинался, но, так уж и быть, отвечаю ещё раз.
Ответ:
Алгебра — мощнейший инструмент для работы с формулами! Для решения уравнений (и неравенств). И особенно — решения задач! Самых разных! Кстати, не только по математике, но и по физике, химии, экономике и другим точным наукам.)
В том числе алгебра нужна и для решения обычных житейских задач. Из реальной повседневной жизни, да.)
И вы в магазине решаете такую житейскую задачку: сколько надо заказать квадратных плиток «n» со стороной «a» см, чтобы облицевать весь пол в ванной и использовать все плитки полностью, ни одну не разрезая?
Для решения этой житейской задачки вполне достаточно обычной школьной алгебры!
Итак, нам известна площадь всей ванной комнаты. Это 4 квадратных метра. Или просто 4. Постоянное число. Также нам известна длина стороны плитки. Это «a» сантиметров. Переменная величина. Ибо длину стороны плиточки мы с вами подбираем. Не знаем мы точного значения… Поэтому вместо циферки вводим буковку, да.) И ещё есть количество этих самых плиточек «n». Тоже буковка, да. Ибо конкретного количества-то плиточек мы тоже не знаем!)
Как составить алгебраическое выражение (формулу) для решения задачи?
Подключаем житейскую логику и здравый смысл. Площадь всей ванной знаем? Знаем! Это 4 (квадратных метра). Площадь комнат в квартире она обычно в квадратных метрах измеряется, да…)
Запоминаем раз и навсегда:
Все однотипные величины в задачах алгебры (в нашем случае это — площадь) должны быть выражены в одинаковых единицах измерения!
Иначе составленное выражение будет неверным, да…
Поэтому площадь одной плиточки в квадратных метрах составит вот такую величину:
А у нас таких плиточек сколько? Конкретно — не знаем. Но в общем виде — знаем! Это n штук. Я же не зря говорил, что буквы в алгебре — это как бы числа. Только не конкретные, а подразумеваемые. Вот и умножаем эту штуковину на n! Всю целиком:
А теперь, чтобы замостить плитками пол в ванной без зазоров и разрезов, должно выполняться железное равенство:
Где 4 — это наши известные четыре квадратных метра площади ванной комнаты.)
А уж выразить буковку n из полученного равенства (формулы) уже не такая большая проблема даже для нашего начального уровня. Хотя бы по правилам работы с дробями и пропорциями:
Вот мы и составили алгебраическое выражение (или более научно — формулу) для подсчёта заказываемых плиточек.
А теперь начинаем наш подбор. Подойдёт ли нам плиточка размером, скажем, a=20 см? И сколько таких плиточек понадобится заказать? Как подсчитать? Подставляем вместо буквы «a» в выражение двадцатку да и считаем:
То есть n = 100. Отлично! Ровно сто плиток нам понадобится!
А если сторона плитки a=15 см? Что ж, опять подставляем и считаем:
Вот-те раз! Число n получилось дробным! Житейски это значит, что покупать надо 178 плиток, но одну из них придётся резать (болгаркой, например). И не факт, что ровнёхонько получится разрезать: дробь нехорошая, периодическая… Не годится этот вариант совсем. )
А если сторона плитки 16 см?
Опять подставляем вместо буквы «а» число 16 и повторяем расчёт:
Уже получше. Понадобится 156 полных плиток и ещё четвертинка! Итого 157 плиток. А одну — распиливать на 4 части и брать один кусочек.
Улавливаете идею? Конечно же, самый лучший вариант — когда всё выражение делится нацело! В нашем случае это будет 100 плиток со стороной 20 см.
Видите, какая интересная математическая дуэль у нас с вами разразилась!
Вообще-то, то чем мы с вами только что занимались, называется составлением математической модели задачи. Или математическим моделированием. А алгебра и её методы — верный и надёжный спутник и помощник для математического моделирования и решения такого рода задачек! Намёк понятен? 🙂 Но задачи и их математические модели — это большая тема отдельного урока… А здесь — лишь ознакомительная демоверсия.)
Вообще говоря, если более глубоко подумать, то задачка эта не такая уж и простая, как может показаться. Во-первых, кто сказал, что ванная комната обязательно должна быть именно прямоугольной формы? Это раз. Во-вторых, даже если пол и прямоугольный, то кто сказал, что его размеры обязательно делятся нацело на длину стороны плитки? Это два. Так что вопрос, придётся или не придётся какие-то плитки распиливать (и сколько конкретно плиток распиливать) зависит не только от соотношения площадей, да… Но и от формы пола и его размеров.) Но для прикидочной оценки (сколько вообще плиток заказывать) даже такого грубого подсчёта вполне достаточно.
Что, сложная задачка? Ладно, ремонт в ванной не каждый день делаем, зато за продуктами ходим регулярно. Вот вам задачка попроще. Для отдыха.) Даже не задачка, считать ничего не будем, а лишь так, поразмышляем.
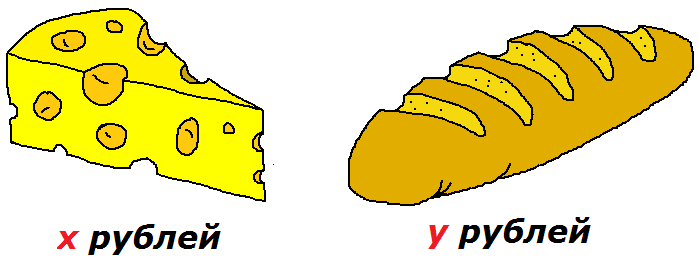
Сыр стоит х рублей, а батон хлеба — у рублей. Каков смысл выражений:
Вот и поразмыслим… Как вы думаете, если вы захотите купить один кусок сыра и один батон хлеба, что вы будете делать, дабы узнать стоимость всей покупки? Конечно! Вы просто сложите цену сыра (х) и цену хлеба (у)! Получится х+у. А уж сколько там сыр с хлебом конкретно стоят в рублях — от конкретного магазина или продавца зависит… А перед алгеброй все магазины и все цены равны: икс плюс игрек — и всё тут.) Вот вам и весь смысл первого выражения.
Уверен теперь, что следующее выражение 2х+3у вас уже не поставит в тупик. За продуктами все ходим.) Догадались? Да! Это будет общая стоимость двух кусков сыра (2х) и трёх батонов хлеба (3у). Улавливаете?)
А х-у? Не всех осеняет сразу… Это выражение ответит нам на вопрос: «На сколько рублей кусок сыра дороже батона хлеба?»
И, наконец, последнее выражение х:у. А за ним какой вопрос скрывается? Правильно! Во сколько раз кусок сыра дороже батона хлеба? Или: «Во сколько раз батон хлеба дешевле куска сыра?» Что одно и то же, да.)
Видите? Каков вопрос задачи, такое и алгебраическое выражение составить надо. Для конкретного вопроса — своё выражение. Но — в общем виде, через буквы. Придём в магазин, посмотрим на ценники, подставим конкретные числа и подсчитаем значение нужного нам выражения. Вот и вся суть.)
А сейчас порешаем простенькие задания самостоятельно. Для привыкания.
3. Время движения лодки по течению реки задаётся формулой t = S:(х+y), где S — расстояние в километрах, х — собственная скорость лодки в км/ч и у — скорость течения реки в км/ч. Пользуясь этой формулой, ответьте на вопросы:
а) Сколько минут плыла лодка 11 км по реке с течением 0,5 км/ч и собственной скоростью 21,5 км/ч?
б) Сколько часов она будет плыть 55 км?
в) Какое расстояние в километрах она проплывёт за пять часов?
Всё получилось? Естественно, уж проще некуда! Что-то не сошлось? Бывает… Внимательнее читаем задание! Где-то время требуется в часах, а где-то часы в минуты надо перевести, да…)
Итак, мы выяснили, что, в отличие от арифметики, в алгебре к числам примешиваются ещё и буквы. Под которыми тоже подразумеваются какие-то числа. Или даже другие выражения. А из этих чиселок и буковок уже можно конструировать самые разнообразные более сложные выражения! Алгебраические выражения.) Простейшие алгебраические выражения и базовые понятия всей алгебры — это одночлен и многочлен. Разберёмся?) В следующем уроке.
Числовые и буквенные выражения
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Числовые выражения: что это
Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.
Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.
Например:
Это простые числовые выражения.
Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:
Это сложные числовые выражения.
Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».
Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.
Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.
11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.
При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)
Часто бывает нужно сравнить два числовых выражения.
Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.
Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2
14 больше 4
14 > 4
6 + 8 > 2 * 2
Буквенные выражения
Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.
В буквенном выражение есть цифры, знаки арифметических действия и буквы.
Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.
Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.
У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:
Пример 1. Найдите значение выражения: 5 + x.
Пример 2. Найдите значение выражения: (4 + a) * (2 + x).
Выражения с переменными
Переменная — это значение буквы в буквенном выражении.
Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.
Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.
5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a
Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.
Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.
Задание раз.
Задание два.
Составьте буквенное выражение:
Сумма разности b и 345 и суммы 180 и x.
Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.
Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?
150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.
Ответ: Маша и Лена посмотрели всего 313 видео.
Числовые и буквенные выражения. Формулы
Так же, как и у нашего языка общения есть алфавит и знаки-помощники (точка, тире, запятая и т.д.), математический язык вычисления также имеет свой алфавит:
Буквы и цифры в математике служат для обозначения чисел.
Цифрами обозначается конкретное, какое-то определённое число.
Буквами – любое или неизвестное число, в зависимости от задачи.
МАТЕМАТИЧЕСКИЕ ВЫРАЖЕНИЯ – это «слова» и «фразы» математики, записи, в которых содержатся:
При этом знаки математических действий и вспомогательные знаки ОБЯЗАТЕЛЬНО связывают числа и обозначают последовательность действий над ними.
Примеры математических выражений:
ВНИМАНИЕ!
НЕ ЯВЛЯЕТСЯ математическим выражением:
Например, это НЕ математические выражения:
Случаи опускания знака умножения в выражениях
В буквенных выражениях обычно знак умножения пишут только между числами, которые выражены цифрами.
В остальных случаях знак умножения опускают, например:
Как читать математические выражения
Простейшие математические выражения, состоящие из одного математического действия, называются по названию результата этого действия:
Более сложные выражения, называют по последнему выполняемому действию:
Важно не только уметь читать готовые математические выражения, но и «переводить» слова на математический язык – язык чисел, знаков действия и других символов:
Алгоритм чтения математических выражений
Чтобы прочитать математическое выражение, нужно:
При чтении сложного выражения повторяем действия алгоритма столько раз, сколько необходимо.
Формулы
Используя математические выражения можно одну величину представить в виде другой, то есть, установить зависимость значения одной величины от значения другой величины.
Велосипедист едет со скоростью \(v_<1>\) км/ч. Найти скорость:
а) автомобиля, если известно, что он едет в 3 раза быстрее: \(v_=3\cdot v_<1>\);
б) пешехода, если известно, что он двигается на 15 км/ч медленнее: \(v_
= v_<1>-15\).
Иначе это называется выразить одну величину через другую.
Многие величины в математике имеют свои собственные обозначения. Например: S – площадь фигуры, P – периметр, t – время и т.д.
Запись такого равенства называется формулой.
ФОРМУЛА – это запись зависимости значения некоторой величины от значений одной или нескольких других величин. Или другими словами, это запись правила вычисления одной неизвестной величины при помощи известных других.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 3.3 / 5. Количество оценок: 8