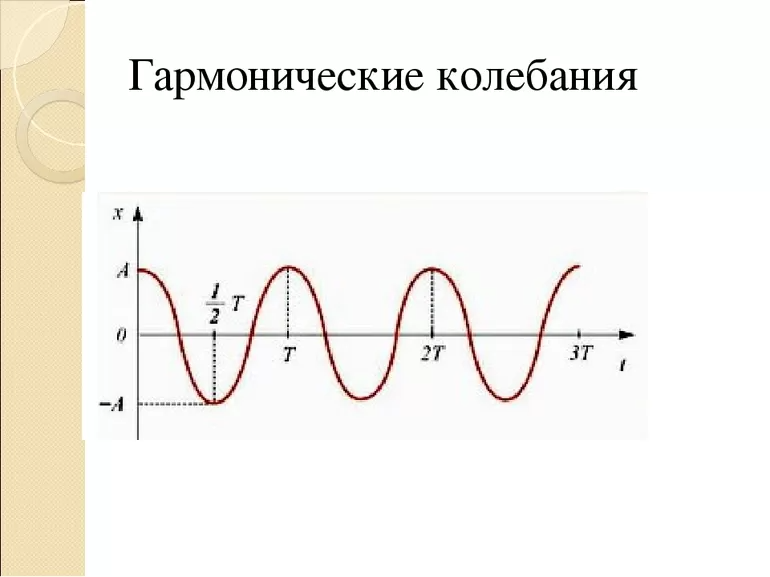
Что в нашей жизни можно описать законом гармонических колебаний

Основные характеристики гармонических колебаний

Что такое гармонические колебания в физике

Гармонические колебания и их характеристики изучает отдельный раздел физики. Основу данных процессов составляет величина, изменяемая в течение определенного временного интервала (периода), согласно косинусоидальному или синусоидальному (гармоническому) закону.

В течение одного периода тело может совершать различные движения:

Данные изменения отражает график. Они могут быть:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Гармонические колебания являются такими колебаниями, при которых характеристики движения в виде координаты, скорости и ускорения изменяются, согласно закону синуса или косинуса.

Колебания представляют собой процессы, которые обладают индивидуальными особенностями в зависимости от степени повторяемости. В качестве примера можно привести качели, ветку дерева, фазы луны, морские приливы и отливы, пульсовые волны, сердце, гортань. В технике и окружающем мире часто можно встретить периодические или близкие к ним процессы, повторяющиеся через одинаковое время. Данные процессы относят к колебательным.

Таким образом, колебаниями является процесс, характеризуемый физической величиной, последовательно изменяющейся в ту или иную сторону относительно некоторого своего среднего значения. К примеру, на качелях, которые подвешены на веревках, человек отклоняется либо вперед и вверх, либо назад и вверх, относительно равновесного положения. В таком случае, качели являются колебательной системой.

Колебательный процесс в системе возникает при воздействии внутренних или внешних сил. Когда в системе наблюдаются колебания, являющиеся результатом внутреннего воздействия, их называют свободными. В том случае, когда колебания тела повторяются через определенное время, их относят к периодическим. Для возникновения свободных колебаний необходимы следующие условия:

Основные характеристики

Колеблющийся на пружине груз обладает определенным ускорением. Данная величина пропорциональна его смещению от равновесного положения:

С другой стороны, ускорение является второй производной координаты. Таким образом, в случае наблюдения свободных колебаний, координата изменяется в течение времени так, что вторая производная координаты по времени будет прямо пропорциональна рассматриваемой координате и обладать противоположным ей знаком:

Вид уравнения гармонических колебаний определяется начальными условиями. Характер колебательного движения зависит от амплитуды, являющейся расстоянием, на которое в начальный момент времени отклонилось тело от равновесного положения. Обозначение амплитуды: x_. Исходя из этого, функция будет преобразована следующим образом:

В результате уравнение для описания свободных колебаний будет иметь вид:

Постоянную величину можно обозначить \(\omega _<0>\)

Тогда уравнение примет вид:

Уравнение движение, описывающее свободные колебания:

Период и частота гармонических колебаний

Минимальное время Т, спустя которое движение тела полностью повторяется, является периодом колебания.

Если известен период колебания, то можно рассчитать частоту колебаний.

Частота колебаний представляет собой число колебаний за единицу времени.

Связь между периодом и частотой колебаний можно записать в виде уравнения:

Исходя из этого, \(\omega _<0>\) является числом колебаний тела за \(2\pi\) секунд. Данную характеристику называют циклической или круговой частотой. Частота свободных колебаний является собственной частотой колебательной системы.

Зависимость частоты и периода свободных колебаний от свойств системы

Существует связь между циклической частотой, периодом и частотой колебаний. Из этого можно заключить, что период и частота также определяются свойствами системы:

Фаза колебаний

При известной амплитуде гармонических колебаний движущееся тело будет иметь координату в какой-либо момент времени, которая определяется аргументом косинуса или синуса. Данный аргумент можно записать так:

Фаза определяет при заданной амплитуде состояния колебательной системы в любой момент времени.

Если колебания обладают одинаковой частотой и амплитудой, то они могут отличаться друг от друга фазами. Формула фазы:

С помощью \(\frac\) можно определить, какая часть временного периода прошла с момента начала колебательных движений. Для любого момента времени, выраженного в долях периода, характерно значение фазы, выраженное в радианах. Графически зависимость координаты точки, совершающей колебания, от фазы можно изобразить в виде косинусоиды либо синусоиды. Аргументом функции при этом будет фаза, выраженная в радианах.

Превращение энергии при гармонических колебаниях

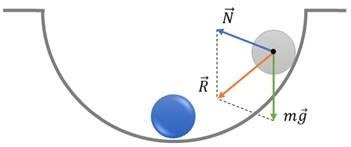
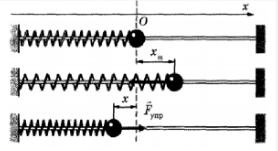
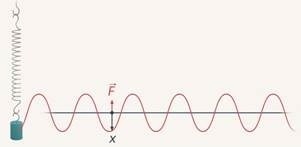
При описании энергетических превращений в данном случае допустимо пренебречь силой трения. Можно рассмотреть следующую ситуацию:

Если шарик отпустить, то это приведет к возникновению силы упругости. Под ее воздействием тело будет двигаться в левую сторону. Когда шарик проходит через положение равновесия в первый раз, его потенциальная энергия принимает нулевое значение, а кинетическая энергия достигает максимума при максимальной скорости:

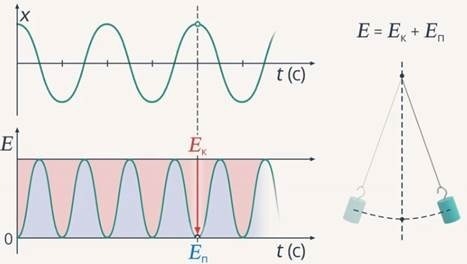
При преодолении точки О шарик удаляется от равновесного положения, наблюдается рост потенциальной энергии. При этом уменьшается кинетическая энергия. Крайнее левое положение тела характеризуется нулевой кинетической энергией и максимальной потенциальной энергией. Закон сохранения энергии будет записан следующим образом:

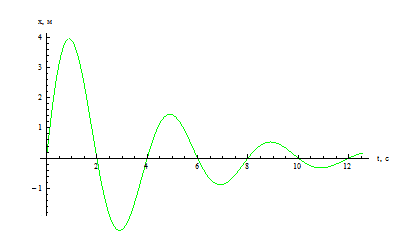
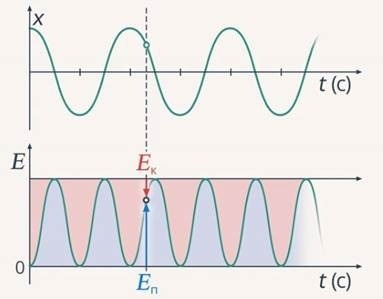
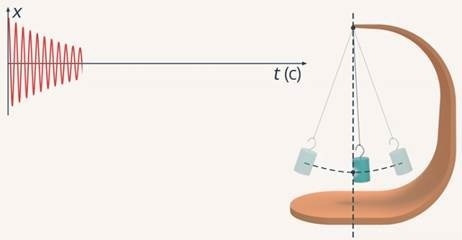
В реальности свободные колебания всегда затухают за счет действия силы трения. Механическая энергия частично рассеивается, как тепло. Пример подобного процесса изображен на графике:

Резонанс

Наиболее простым способом сформировать незатухающие колебания служит воздействие на систему внешней периодической силы. Данные колебания называют вынужденными. Благодаря притоку энергии извне, колебательные движения продолжаются без остановки, даже с учетом действия сил трения.

В качестве примера можно рассмотреть качели, отклоняемые от точки равновесия толчком. Каждый последующий толчок увеличивает амплитуду колебаний качелей до тех пор, пока она не достигнет максимума. Описываемое явление называют резонансом.

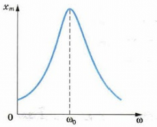
Резонанс — резкое возрастание амплитуды вынужденных колебаний, происходящее при совпадении частоты изменения внешней силы, действующей на систему, с частотой свободных колебаний.

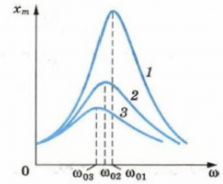
Графически резонанс можно представить в виде резкого скачка графика в верхнем направлении. Амплитуда колебаний определяется величиной сил трения. Чем больше сила трения, тем меньше при резонансе возрастает амплитуда вынужденных колебаний. Процесс проиллюстрирован на графиках. На первом графике можно наблюдать ситуацию с минимальным трением, а на третьем – с максимальным.

Описание графика, применение маятников

Гармонические колебания обладают важным признаком, который заключается в том, что период колебаний не зависит от их частоты. В качестве моделей для демонстрации гармонических колебаний используют:

Предположим, что возвращающей силой является сила упругости, которая определяется по формуле:

где x – является отклонением от положения равновесия;

k – это коэффициент упругости.

Согласно второму закону Ньютона:

Если разделить полученное уравнение на массу, то получится выражение для определения ускорения колеблющегося тела:

При известной угловой частоте, исходя из выведенной записи второго закона Ньютона, линейную частоту или период колебаний можно рассчитать так:

Аналогичным способом можно определить угловую частоту для математического маятника. Кроме того, при колебательных движениях действует закон сохранения энергии.

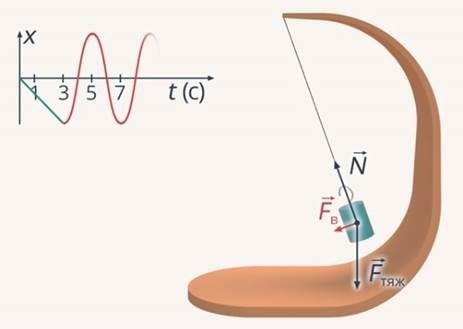
Вызвать колебательные движения маятника, которые являются гармоническими, можно с помощью двух методов. В первом случае груз из равновесного положения выводят, а затем отпускают. Такое движение графически изображено на рисунке.

Второй способ заключается в придании телу импульса, после чего оно будет совершать гармонические колебания. К примеру, можно толкнуть предмет или раскачать качели, вначале выводя их из равновесного положения, а затем, отпустив. В любом промежуточном значении маятника сумма кинетической и потенциальной энергии будет равна начальной энергии рассматриваемого маятника.

В реальности маятники, способные достаточно долго колебаться, не существуют. Такая ситуация является абстракцией.

Система маятников не является замкнутой по причине наличия силы трения. Действие этой силы способствует энергетическим потерям во время колебательных движений маятника.

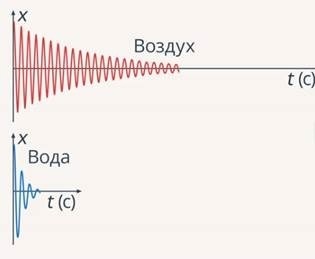
Силы трения могут быть внешними и внутренними. В первом случае, это окружающий воздух или другая среда. Внутренняя сила может быть в подвесе маятника.

В результате амплитуда колебаний будет уменьшаться. В итоге это приведет к полной остановке маятника. При этом колебания будут затухающими.

Затухающие колебания – колебания, происходящие в незамкнутой системе, в том числе под действием силы трения.

Амплитуда таких колебаний с течением времени затухает. Большинство колебаний в окружающей среде относятся к затухающим колебаниям из-за постоянного присутствия сил трения.

Какое уравнение выражает смысл гармонического колебания

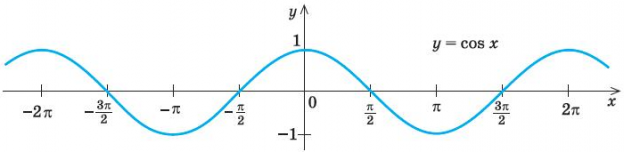
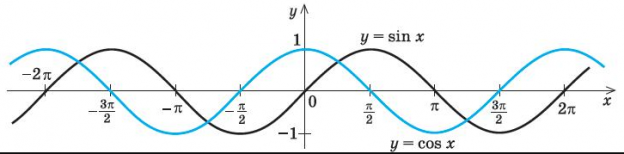
Согласно определению, гармонические колебания обладают кинематическими характеристиками, которые меняются по закону синуса или косинуса.

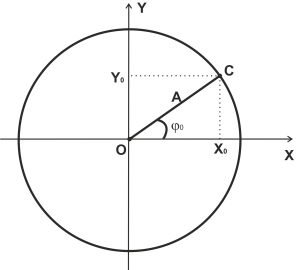
Визуализировать гармонические колебания можно, представив вращательное движение как колебательное движение вдоль двух осей, которые взаимно перпендикулярны. Предположим, что тело вращается по окружности с радиусом А. Начальное его положение совпадает с точкой С. В начале движения радиус-вектор, который описывает рассматриваемую точку, расположен под углом \(\varphi _<0>\) к оси ОХ.

По проекциям радиуса на оси можно рассчитать начальные координаты:

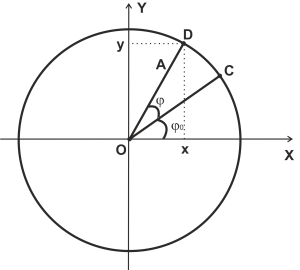
Можно предположить, что, спустя время t, тело, обладая угловой скоростью \omega, переместилось в точку D. В этом случае угол поворота радиус-вектора относительно начального положения равен \(\varphi.\) Текущие координаты тела будут равны:

\(x=A\cos (\varphi +\varphi _<0>)\)

\(y=A\sin (\varphi +\varphi _<0>)\)

Если речь идет о равномерном движении тела по окружности, то:

\(x=A\cos (\omega*t +\varphi _<0>)\)

\(y=A\sin (\omega*t +\varphi _<0>)\)

Записанные равенства представляют собой закон движения материальной точки, которая совершает гармонические колебания в контуре. Если \(\sin (90^<0>-\alpha )=\cos \alpha,\) то уравнение можно преобразовать следующим образом:

\(x=A\cos (\omega*t +\varphi _<0>)=A\sin (\omega*t-90^ <0>+\varphi _<0>)=A\sin (\omega t+\varphi ^<,>_<0>)\)

где \(\varphi ^<,>_ <0>= \varphi _<0>-90^<0>\) является новым параметром, характеризующим некое другое начальное положение тела.

Исходя из представленных закономерностей, следует, что записанные уравнения являются в теории одинаковыми при разных начальных условиях. В качестве примера можно разобрать только первое уравнение. Каждый из введенных параметров, имея аналог во вращательном движении, описывается по-другому в колебательном движении:

\(x=A\cos (\omega*t +\varphi _<0>)\)

х — является текущей координатой тела;

А — это амплитуда колебаний (максимальное отклонение тела от положения равновесия);

\(\omega\) — определяет циклическую частоту колебания;

t — является временем движения;

\(\varphi _<0>)\) — представляет собой начальную фазу колебания;

\((\omega*t +\varphi _<0>) \) — текущая фаза колебания (все, что стоит под тригонометрической функцией).

Обладая информацией об общем виде колебательного движения, можно определить зависимость скорости и ускорения от времени:

\(x=A\cos (\omega*t +\varphi _<0>)\)

\(v_=-A\omega \sin(\omega*t +\varphi _<0>)\)

где \(v_\) является скоростью тела, \(a_\) – это его ускорение.

Данное уравнение является основным уравнением гармонических колебаний, которое часто встречается при решении задач.

Применение гармонических колебаний в жизни

Колебания часто встречаются в природе и технике. Как и вращение, колебательные процессы являются основой развития таких отраслей, как электротехника и радиотехника. Зачастую колебания носят негативный характер. К примеру, вибрируют крылья самолета, корпуса судов, здания и сооружения из-за резонанса с эксплуатируемым там оборудованием. Данное обстоятельство учитывают инженеры при реализации подобных проектов.

Колебания используют при создании музыкальных инструментов. Например, струны колеблются под руками музыканта, что вызывает колебания воздуха, и окружающие слышат звуки музыки.

Многие важные внутренние процессы в организме человека относят к колебательным. Например, человеческое сердце, находясь в состоянии покоя, совершает приблизительно одно колебательное движение в течение секунды. Повторяющиеся нервные импульсы провоцируют непрерывное сокращение и растягивание мышц. Люди слышат и говорят, благодаря колебаниям.

Свет также обладает колебательной природой. Кроме того, и атомы совершают колебательные движения. Гармоничные колебания тока активно применяются в производстве технических приборов.

В радиотехнике и электросвязи широко используют гармонические сигналы от долей Гц (инфранизкие частоты) до десятков и сотен ГГц (сверхвысокие частоты). Разнообразные звуки и изображения транспортируются на удаленные расстояния, благодаря электромагнитным волнам.

Электромагнитные волны образуются в результате существования переменного тока с высокой частотой определенного напряжения, который подводят к передатчику, а для получения высокочастотного переменного тока используются электронные генераторы, входящие в конструкцию радиопередатчика.

Источник