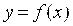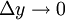что значит функция дифференцируема в точке
Что значит функция дифференцируема в точке
3.2.3. дЙЖЖЕТЕОГЙТХЕНПУФШ ЖХОЛГЙК. оЕРТЕТЩЧОПУФШ ДЙЖЖЕТЕОГЙТХЕНПК ЖХОЛГЙЙ
еУМЙ ЖХОЛГЙС ДЙЖЖЕТЕОГЙТХЕНБ Ч ЛБЦДПК ФПЮЛЕ ОЕЛПФПТПЗП ПФТЕЪЛБ [ Б ; b ] ЙМЙ ЙОФЕТЧБМБ ( Б ; b ), ФП ЗПЧПТСФ, ЮФП ПОБ ДЙЖЖЕТЕОГЙТХЕНБ ОБ ПФТЕЪЛЕ [ Б ; b ] ЙМЙ УППФЧЕФУФЧЕООП Ч ЙОФЕТЧБМЕ ( Б ; b ).
уРТБЧЕДМЙЧБ УМЕДХАЭБС ФЕПТЕНБ, ХУФБОБЧМЙЧБАЭБС УЧСЪШ НЕЦДХ ДЙЖЖЕТЕОГЙТХЕНЩНЙ Й ОЕРТЕТЩЧОЩНЙ ЖХОЛГЙСНЙ.
фБЛЙН ПВТБЪПН, ЙЪ ДЙЖЖЕТЕОГЙТХЕНПУФЙ ЖХОЛГЙЙ УМЕДХЕФ ЕЕ ОЕРТЕТЩЧОПУФШ.
еУМЙ 
, ФП 
ЗДЕ 
ВЕУЛПОЕЮОП НБМБС ЧЕМЙЮЙОБ, Ф.Е. ЧЕМЙЮЙОБ, УФТЕНСЭБСУС Л ОХМА РТЙ 
. оП ФПЗДБ
фБЛЙН ПВТБЪПН, Ч ФПЮЛБИ ТБЪТЩЧБ ЖХОЛГЙС ОЕ НПЦЕФ ЙНЕФШ РТПЙЪЧПДОПК. пВТБФОПЕ ХФЧЕТЦДЕОЙЕ ОЕЧЕТОП: УХЭЕУФЧХАФ ОЕРТЕТЩЧОЩЕ ЖХОЛГЙЙ, ЛПФПТЩЕ Ч ОЕЛПФПТЩИ ФПЮЛБИ ОЕ СЧМСАФУС ДЙЖЖЕТЕОГЙТХЕНЩНЙ (Ф.Е. ОЕ ЙНЕАФ Ч ЬФЙИ ФПЮЛБИ РТПЙЪЧПДОПК).
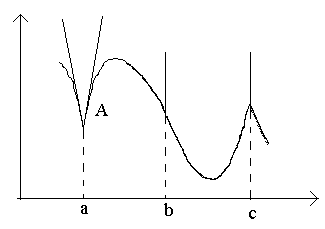
тБУУНПФТЙН ОБ ТЙУХОЛЕ ФПЮЛЙ Б, b, c.
ч ФПЮЛЕ b РТЙ ПФОПЫЕОЙЕ 
СЧМСЕФУС ЪОБЛПРПУФПСООПК ВЕУЛПОЕЮОП ВПМШЫПК ЧЕМЙЮЙОПК 
.
жХОЛГЙС ЙНЕЕФ ВЕУЛПОЕЮОХА РТПЙЪЧПДОХА. ч ЬФПК ФПЮЛЕ ЗТБЖЙЛ ЙНЕЕФ ЧЕТФЙЛБМШОХА ЛБУБФЕМШОХА. фЙР ФПЮЛЙ – «ФПЮЛБ РЕТЕЗЙВБ» c ЧЕТФЙЛБМШОПК ЛБУБФЕМШОПК.
ч ФПЮЛЕ c ПДОПУФПТПООЙЕ РТПЙЪЧПДОЩЕ СЧМСАФУС ВЕУЛПОЕЮОП ВПМШЫЙНЙ ЧЕМЙЮЙОБНЙ ТБЪОЩИ ЪОБЛПЧ. ч ЬФПК ФПЮЛЕ ЗТБЖЙЛ ЙНЕЕФ ДЧЕ УМЙЧЫЙЕУС ЧЕТФЙЛБМШОЩЕ ЛБУБФЕМШОЩЕ. фЙР – «ФПЮЛБ ЧПЪЧТБФБ» У ЧЕТФЙЛБМШОПК ЛБУБФЕМШОПК – ЮБУФОЩК УМХЮБК ХЗМПЧПК ФПЮЛЙ.
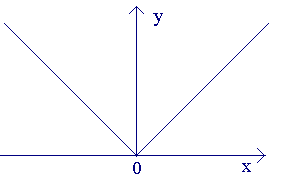
тБУУНПФТЙН ЖХОЛГЙА y=|x|.
ьФБ ЖХОЛГЙС ОЕРТЕТЩЧОБ Ч ФПЮЛЕ x = 0, Ф.Л. 
.
рПЛБЦЕН, ЮФП ПОБ ОЕ ЙНЕЕФ РТПЙЪЧПДОПК Ч ЬФПК ФПЮЛЕ.
оП ФПЗДБ РТЙ 
б РТЙ > 0
ф.П., ПФОПЫЕОЙЕ 
РТЙ 
УРТБЧБ Й УМЕЧБ ЙНЕЕФ ТБЪМЙЮОЩЕ РТЕДЕМЩ, Б ЬФП ЪОБЮЙФ, ЮФП ПФОПЫЕОЙЕ РТЕДЕМБ ОЕ ЙНЕЕФ, Ф.Е. РТПЙЪЧПДОБС ЖХОЛГЙЙ y=|x| Ч ФПЮЛЕ x = 0 ОЕ УХЭЕУФЧХЕФ. зЕПНЕФТЙЮЕУЛЙ ЬФП ЪОБЮЙФ, ЮФП Ч ФПЮЛЕ x = 0 ДБООБС «ЛТЙЧБС» ОЕ ЙНЕЕФ ПРТЕДЕМЕООПК ЛБУБФЕМШОПК (Ч ЬФПК ФПЮЛЕ ЙИ ДЧЕ).
Что значит функция дифференцируема в точке
При дифференцировании различают функции по способу их задания: явные, неявные и параметрические.
Производной функции y = f ( x ) по переменной x в некоторой точке называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю, то есть
Производная характеризует скорость изменения функции в достаточно малой окрестности заданной точки.
Приведем таблицу производных основных элементарных функций (без доказательства), которые рассматриваются нами как функции простые и явно заданные.
Следствие. В точках разрыва функция производной не имеет 
Существуют такие точки, в которых функция непрерывна, но не дифференцируема. Так, функция y =| x | в точке x =0 непрерывна, но производной не имеет, так как в этой точке к графику функции можно провести бесконечное множество касательных (рис. 3.6). Такие точки называются угловыми или точками излома функции. Данный случай показывает, что обратное утверждение к теореме 3.9 неверно.
Среди явных функций особое место занимают обратные функции, производная которых находится с помощью следующей теоремы.
Теорема 3.10. Если строго монотонная функция y = f ( x ) дифференцируема на некотором интервале Х, причем ее производная не обращается в нуль на Х, то обратная к ней функция x = φ ( y ) также дифференцируема на этом интервале, при этом:
По определению производной можно записать:
Среди явных функций выделяют класс сложных функций.
Теорема 3.11. Чтобы продифференцировать сложную функцию необходимо сначала продифференцировать внешнюю функцию по внутренней, считая внутреннюю функцию независимой переменной, затем продифференцировать внутреннюю функцию по независимому переменному и результаты дифференцирования перемножить, то есть
Решение. Согласно формуле (3.31) и с учетом табли 
чных формул (3.17), (3.19), (3.29) имеем:
где t – параметр. Производную такой функции несложно получить:
Пример 3.9. Найти производную функции 
.
Решение. Согласно формуле (3.32) и с учетом табличных формул (3.18), (3.19) имеем:
Помимо таблицы производных имеют место правила дифференцирования.
Теорема 3.12. Производная суммы двух дифференцируемых функций равна сумме производных этих функций:
Данная теорема может быть обобщена для произвольного конечного числа функций-слагаемых.
Решение. Согласно формулам (3.33) и (3.31) и с учетом табличных формул (3.17), (3.20), (3.23) имеем:
Теорема 3.13. Производная произведения двух дифференцируемых функций равна произведению производной первой функции-сомножителя на вторую функцию плюс произведение первой функции на производную второй функции–сомножителя, то есть
Решение. Согласно формуле (3.34) и с учетом табличных формул (3.22), (3.24) имеем:
Теорема 3.14. Производная частного двух функций равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а числитель есть разность между произведением знаменателя на производную числителя и произведением числителя на производную знаменателя, то есть
Решение. Согласно формуле (3.35) и с учетом табличных формул (3.17), (3.29) имеем:
Решение. Согласно формуле (3.31) дифференцирования сложной функции и (3.34) производной произведения, с учетом табличных формул (3.17) и (3.18) имеем:
Дифференциалом функции y = f ( x ) в точке x называется главная часть приращения этой функции, равная произведению производной функции на приращение аргумента:
Формула (3.39) применяется для вычисления приближенных значений функций.
Дифференцируемость функции в точке, связь с непрерывностью.
Дифференциал функции.
1. Дифференцируемость функции в точке, связь с непрерывностью.
2. Дифференциальная функции, его геометрический смысл.
3. Свойства дифференциала, инвариантность его формы.
4. Дифференциал высших порядков.
Введение.
Дифференцируемость функции в точке, связь с непрерывностью.
Определение.Функция 
называется дифференцируемой в точке 
, если её приращение 
в этой точке можно представить в виде
(1)
где А – некоторое число, не зависящее от 
, а 
— функция аргумента , являющаяся бесконечно малой при 
.
Установим связь между дифференцируемостью функции в точке и существованием производной в этой же точке.
Теорема1. Для того чтобы функция была дифференцируема в необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Таким образом, для функции одной переменной дифференцируемость и существование производной – понятия равносильные. Поэтому операцию нахождения производной часто называют дифференцированием.
Установим связь между понятием дифференцируемости и непрерывности.
Теорема2. Если функция дифференцируема в точке , то она непрерывна в этой точке.
Замечание. Обратное утверждение неверно. Функция может быть непрерывной в точке, но не быть дифференцируемой, т.е. не иметь производной в этой точке.
Например, функция 
непрерывна в точке 
, но производной в этой точке не имеет. Действительно, 
.
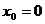
Если функция 
имеет производную в каждой точке некоторого промежутка, то будем говорить, что функция дифференцируема на данном промежутке.
Дифференцируемость функции в точке
Дифференци́руемая фу́нкция в математическом анализе — это функция, которая может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так и в естественных науках, широко использующих математический аппарат.
Содержание
Определения
где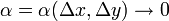 
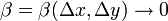
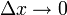
и 
при 
,
Свойства
Касательная прямая
Примеры
См. также
Ссылки
Полезное
Смотреть что такое «Дифференцируемость функции в точке» в других словарях:
Дифференцируемость — Дифференцируемая функция в математическом анализе это функция, которая может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так… … Википедия
Аналитические функции — функции, которые могут быть представлены степенными рядами (См. Степенной ряд). Исключительная важность класса А. ф. определяется следующим. Во первых, этот класс достаточно широк; он охватывает большинство функций, встречающихся в… … Большая советская энциклопедия
Производная функции — У этого термина существуют и другие значения, см. Производная. Иллюстрация понятия производной Производная&# … Википедия
АППРОКСИМАТИВНАЯ ДИФФЕРЕНЦИРУЕМОСТЬ — обобщение понятия дифференцируемости с заменой обычного предела аппроксимативным пределом. Действительная функция действительного переменного наз. аппроксимативно дифференцируемой в точке х 0, если существует такое число А, что При этом величина… … Математическая энциклопедия
Непрерывная дифференцируемость — Дифференцируемая функция в математическом анализе это функция, которая может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так… … Википедия
Показатель Гёльдера — (известен также как показатель Липшица) характеристика гладкости функции. Локальный (точечный) показатель Гёльдера характеризует локальную гладкость (локальную нерегулярность) функции в точке. В общем случае показатель Гёльдера является… … Википедия
Показатель Гельдера — Показатель Гёльдера α (известен также как показатель Липшица) характеристика гладкости функции. Локальный (точечный) показатель Гёльдера характеризует локальную гладкость (локальную нерегулярность) функции в точке. В общем случае показатель… … Википедия
Показатель Липшица — Показатель Гёльдера α (известен также как показатель Липшица) характеристика гладкости функции. Локальный (точечный) показатель Гёльдера характеризует локальную гладкость (локальную нерегулярность) функции в точке. В общем случае показатель… … Википедия
Условие Гельдера — Показатель Гёльдера α (известен также как показатель Липшица) характеристика гладкости функции. Локальный (точечный) показатель Гёльдера характеризует локальную гладкость (локальную нерегулярность) функции в точке. В общем случае показатель… … Википедия
АНАЛИТИЧЕСКАЯ ФУНКЦИЯ — функция, к рая может быть представлена степенным рядом. Исключит, важность класса А. ф. определяется следующим. Во первых, этот класс достаточно ш и р о к: он охватывает большинство функций, встречающихся в основных вопросах математики и ее… … Математическая энциклопедия
4.02. Дифференцируемость функции в точке и на промежутке
Производная функции, согласно ее математического определения (1.5) и (1.6) – это некий предел. Но, как и всякий предел, он может оказаться:
А) конечным; б) бесконечным; в) вообще не существовать.
Если для данного X имеет место вариант (а), то есть если при заданном X производная 
функции 
Существует и конечна, то эта функция называется Дифференцируемой в точке x.
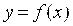
Функция, дифференцируемая в Каждой точке X некоторого промежутка оси Ох (например, интервала (A; B) или отрезка [A; B]) называется Дифференцируемой на этом промежутке. Кстати, сама процедура вычисления производной функции называется ее Дифференцированием (продифференцировать функцию – это значит найти ее производную).
Из геометрического смысла производной функции, определяемого равенством (1.11) и рис. 4.5, вытекают следующие два наглядные необходимые и достаточные условия дифференцируемости заданной функции в заданной точке X:
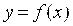
1) Существование касательной к графику функции в его точке с абсциссой X.
2) Невертикальность этой касательной (ибо 
не существует).
Например, функция 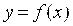, график которой изображен на рис. 4.7, не дифференцируема в точках X1, X2 и X3.
Действительно, точке X1 соответствует на графике функции точка M1 с вертикальной касательной. Точке X2 (точке максимума функции) соответствует остроконечная вершина M2, касательная в которой не существует. Точке X3 соответствует точка M3 – точка излома графика функции, в которой тоже касательная не существует.
Во всех же остальных точках M графика функции касательную к графику провести можно, и она невертикальна. Значит, для всех остальных X, отличных от (X1; X2; X3), существует производная функции. То есть во всех остальных точках X функция дифференцируема.