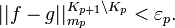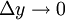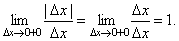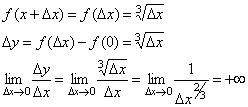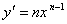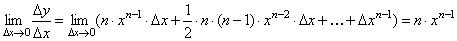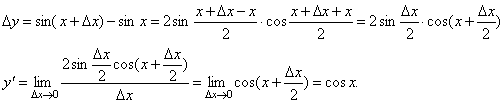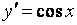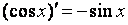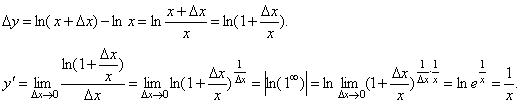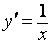что значит непрерывно дифференцируемая функция

Непрерывно дифференцируемая функция

Непрерывно дифференцируемая функция

Случай функций одной переменной

В этом случае непрерывно дифференцируемая функция есть дифференцируемая функция, у которой первая производная непрерывна. Такие функции часто называют гладкими функциями.

Рассматривают также дважды непрерывно дифференцируемые функции — функции имеющие непрерывную вторую производную.

Аналогично можно ввести понятие n раз непрерывно дифференцируемых функций.

Случай функций многих переменной

В этом случае понятие непрерывно дифференцируемой функции может рассматриваться в двух видах:

Приближение непрерывно-дифференцируемых функций аналитическими

Полезное

Смотреть что такое «Непрерывно дифференцируемая функция» в других словарях:

Дифференцируемая функция — [differentiable function] функция, имеющая в каждой точке области, на которой она определена, полный дифференциал, а в случае функции одного переменного производную[1]. Если функция f(x) дифференцируема в точке x, то она и непрерывна в этой точке … Экономико-математический словарь

дифференцируемая функция — Функция, имеющая в каждой точке области, на которой она определена, полный дифференциал, а в случае функции одного переменного производную[1]. Если функция f(x) дифференцируема в точке x, то она и непрерывна в этой точке. Если она дифференцируема … Справочник технического переводчика

Вогнутая функция — Функция(её график выделен синим) выпукла тогда и только тогда когда область над её графиком (закрашено зеленым) является выпуклым множеством. В математике функция называется выпуклой (или выпуклой вниз) на некотором интервале (в общем случае на… … Википедия

Выпуклая функция — Выпуклая функция, её график выделен синим и надграфик закрашен зеленым. Выпуклая функция функция, у которой надграфик является выпуклым множеством … Википедия

Гладкая функция — или непрерывно дифференцируемая функция это функция, имеющая непрерывную производную на всём множестве определения. Основные сведения Рассматривают также гладкие функции высших порядков, а именно, функция с порядком гладкости имеет… … Википедия

ЛЯПУНОВА ФУНКЦИЯ — функция, определяемая следующим образов. Пусть х 0 неподвижная точка системы дифференциальных уравнений (т. е. ), где отображение непрерывной непрерывно дифференцируемо по х(здесь U нек рая окрестность точки х 0 в ); в координатах эта система… … Математическая энциклопедия

ОБОБЩЁННАЯ ФУНКЦИЯ — матем. понятие … Физическая энциклопедия

АНАЛИТИЧЕСКАЯ ФУНКЦИЯ — функция, к рая может быть представлена степенным рядом. Исключит, важность класса А. ф. определяется следующим. Во первых, этот класс достаточно ш и р о к: он охватывает большинство функций, встречающихся в основных вопросах математики и ее… … Математическая энциклопедия

Источник

Что значит непрерывно дифференцируемая функция

3.2.3. дЙЖЖЕТЕОГЙТХЕНПУФШ ЖХОЛГЙК. оЕРТЕТЩЧОПУФШ ДЙЖЖЕТЕОГЙТХЕНПК ЖХОЛГЙЙ

еУМЙ ЖХОЛГЙС ДЙЖЖЕТЕОГЙТХЕНБ Ч ЛБЦДПК ФПЮЛЕ ОЕЛПФПТПЗП ПФТЕЪЛБ [ Б ; b ] ЙМЙ ЙОФЕТЧБМБ ( Б ; b ), ФП ЗПЧПТСФ, ЮФП ПОБ ДЙЖЖЕТЕОГЙТХЕНБ ОБ ПФТЕЪЛЕ [ Б ; b ] ЙМЙ УППФЧЕФУФЧЕООП Ч ЙОФЕТЧБМЕ ( Б ; b ).

уРТБЧЕДМЙЧБ УМЕДХАЭБС ФЕПТЕНБ, ХУФБОБЧМЙЧБАЭБС УЧСЪШ НЕЦДХ ДЙЖЖЕТЕОГЙТХЕНЩНЙ Й ОЕРТЕТЩЧОЩНЙ ЖХОЛГЙСНЙ.

фБЛЙН ПВТБЪПН, ЙЪ ДЙЖЖЕТЕОГЙТХЕНПУФЙ ЖХОЛГЙЙ УМЕДХЕФ ЕЕ ОЕРТЕТЩЧОПУФШ.

еУМЙ , ФП

ЗДЕ ВЕУЛПОЕЮОП НБМБС ЧЕМЙЮЙОБ, Ф.Е. ЧЕМЙЮЙОБ, УФТЕНСЭБСУС Л ОХМА РТЙ . оП ФПЗДБ

фБЛЙН ПВТБЪПН, Ч ФПЮЛБИ ТБЪТЩЧБ ЖХОЛГЙС ОЕ НПЦЕФ ЙНЕФШ РТПЙЪЧПДОПК. пВТБФОПЕ ХФЧЕТЦДЕОЙЕ ОЕЧЕТОП: УХЭЕУФЧХАФ ОЕРТЕТЩЧОЩЕ ЖХОЛГЙЙ, ЛПФПТЩЕ Ч ОЕЛПФПТЩИ ФПЮЛБИ ОЕ СЧМСАФУС ДЙЖЖЕТЕОГЙТХЕНЩНЙ (Ф.Е. ОЕ ЙНЕАФ Ч ЬФЙИ ФПЮЛБИ РТПЙЪЧПДОПК).

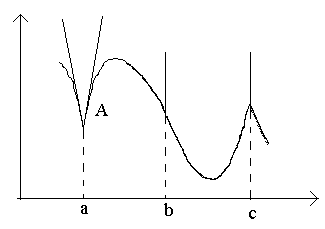
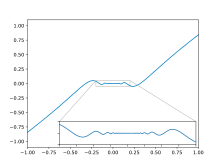
тБУУНПФТЙН ОБ ТЙУХОЛЕ ФПЮЛЙ Б, b, c.

ч ФПЮЛЕ b РТЙ ПФОПЫЕОЙЕ СЧМСЕФУС ЪОБЛПРПУФПСООПК ВЕУЛПОЕЮОП ВПМШЫПК ЧЕМЙЮЙОПК .

жХОЛГЙС ЙНЕЕФ ВЕУЛПОЕЮОХА РТПЙЪЧПДОХА. ч ЬФПК ФПЮЛЕ ЗТБЖЙЛ ЙНЕЕФ ЧЕТФЙЛБМШОХА ЛБУБФЕМШОХА. фЙР ФПЮЛЙ – «ФПЮЛБ РЕТЕЗЙВБ» c ЧЕТФЙЛБМШОПК ЛБУБФЕМШОПК.

ч ФПЮЛЕ c ПДОПУФПТПООЙЕ РТПЙЪЧПДОЩЕ СЧМСАФУС ВЕУЛПОЕЮОП ВПМШЫЙНЙ ЧЕМЙЮЙОБНЙ ТБЪОЩИ ЪОБЛПЧ. ч ЬФПК ФПЮЛЕ ЗТБЖЙЛ ЙНЕЕФ ДЧЕ УМЙЧЫЙЕУС ЧЕТФЙЛБМШОЩЕ ЛБУБФЕМШОЩЕ. фЙР – «ФПЮЛБ ЧПЪЧТБФБ» У ЧЕТФЙЛБМШОПК ЛБУБФЕМШОПК – ЮБУФОЩК УМХЮБК ХЗМПЧПК ФПЮЛЙ.

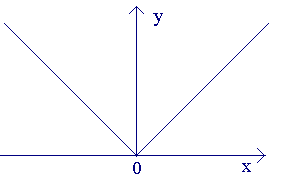
тБУУНПФТЙН ЖХОЛГЙА y=|x|.

ьФБ ЖХОЛГЙС ОЕРТЕТЩЧОБ Ч ФПЮЛЕ x = 0, Ф.Л. .

рПЛБЦЕН, ЮФП ПОБ ОЕ ЙНЕЕФ РТПЙЪЧПДОПК Ч ЬФПК ФПЮЛЕ.

оП ФПЗДБ РТЙ

б РТЙ > 0

ф.П., ПФОПЫЕОЙЕ РТЙ УРТБЧБ Й УМЕЧБ ЙНЕЕФ ТБЪМЙЮОЩЕ РТЕДЕМЩ, Б ЬФП ЪОБЮЙФ, ЮФП ПФОПЫЕОЙЕ РТЕДЕМБ ОЕ ЙНЕЕФ, Ф.Е. РТПЙЪЧПДОБС ЖХОЛГЙЙ y=|x| Ч ФПЮЛЕ x = 0 ОЕ УХЭЕУФЧХЕФ. зЕПНЕФТЙЮЕУЛЙ ЬФП ЪОБЮЙФ, ЮФП Ч ФПЮЛЕ x = 0 ДБООБС «ЛТЙЧБС» ОЕ ЙНЕЕФ ПРТЕДЕМЕООПК ЛБУБФЕМШОПК (Ч ЬФПК ФПЮЛЕ ЙИ ДЧЕ).

Источник

Непрерывная дифференцируемость

Дифференци́руемая фу́нкция в математическом анализе — это функция, которая может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так и в естественных науках, широко использующих математический аппарат.

Содержание

Определения

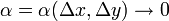
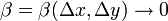
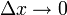
где и при ,

Свойства

Касательная прямая

Примеры

См. также

Ссылки

Полезное

Смотреть что такое «Непрерывная дифференцируемость» в других словарях:

Дифференцируемая функция — Дифференцируемая (в точке) функция это функция, у которой существует дифференциал (в данной точке). Дифференцируемая на некотором множестве функция это функция, дифференцируемая в каждой точке данного множества. Дифференцируемость является… … Википедия

Дифференциальное исчисление — раздел математики, в котором изучаются производные и дифференциалы функций и их применения к исследованию функций. Оформление Д. и. в самостоятельную математическую дисциплину связано с именами И. Ньютона и Г. Лейбница (вторая половина 17 … Большая советская энциклопедия

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ОБЫКНОВЕННОЕ — уравнение, в к ром неизвестной является функция от одного независимого переменного, причем в это уравнение входят не только сама неизвестная функция, но и ее производные различных порядков. Термин дифференциальные уравнения был предложен Г.… … Математическая энциклопедия

ЛИНЕЙНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ В БАНАХОВОМ ПРОСТРАНСТВЕ — уравнение вида где A0(t), A1(t).при каждом t линейные операторы в банаховом пространстве Е, g(t) заданная, a u(t) искомая функции со значениями в Е;производная ипонимается как предел по норме Еразностного отношения. 1. Линейное дифференциальное… … Математическая энциклопедия

Приближение функций комплексного переменного — раздел комплексного анализа, изучающий вопросы приближённого представления (аппроксимации) функций комплексного переменного посредством аналитических функций (См. Аналитические функции) специальных классов. Центральная проблематика… … Большая советская энциклопедия

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — раздел математики, в к ром изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Развитие Д. и. тесно связано с развитием интегрального исчисления. Неразрывно и их содержание. Вместе они составляют основу… … Математическая энциклопедия

Источник

Непрерывность дифференцируемой функции

Функция y = f(x) называется дифференцируемой в некоторой точке x₀, если она имеет в этой точке определенную производную, т.е. если предел отношения 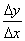существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что она дифференцируема на отрезке [а; b] или соответственно в интервале (а; b).

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Теорема. Если функция y = f(x) дифференцируема в некоторой точке x₀, то она в этой точке непрерывна.

Таким образом, из дифференцируемости функции следует ее непрерывность.

,

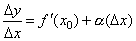
где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx→0. Но тогда

Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).

Рассмотрим на рисунке точки а, b, c.

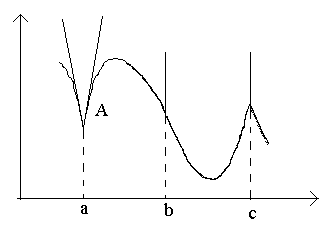
В точке a при Δx→0 отношение 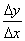не имеет предела (т.к. односторонние пределы различны при Δx→0–0 и Δx→0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к₁ и к₂. Такой тип точек называют угловыми точками.

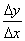
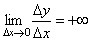
В точке b при Δx→0 отношение является знакопостоянной бесконечно большой величиной . Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки – «точка перегиба» c вертикальной касательной.

В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиеся вертикальные касательные. Тип – «точка возврата» с вертикальной касательной – частный случай угловой точки.

Примеры.

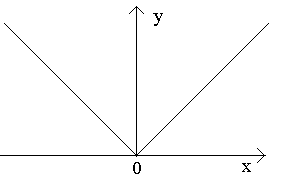
1. Рассмотрим функцию y=|x|. Эта функция непрерывна в точке x = 0, т.к. .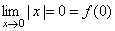

Покажем, что она не имеет производной в этой точке.

Т.о., отношение 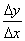при Δx→ 0 справа и слева имеет различные пределы, а это значит, что отношение предела не имеет, т.е. производная функции y=|x| в точке x= 0 не существует. Геометрически это значит, что в точке x= 0 данная «кривая» не имеет определенной касательной (в этой точке их две).

2. Функция определена и непрерывна на всей числовой прямой. Выясним, имеет ли эта функция производную при x= 0.

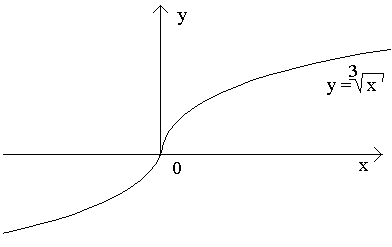
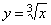
Следовательно, рассматриваемая функция не дифференцируема в точке x= 0. Касательная к кривой в этой точке образует с осью абсцисс угол p/2, т.е. совпадает с осью Oy.

Производные элементарных функций.

можно доказать, что

Заметим, что в каждом из пропущенных слагаемых есть множитель Δx в степени выше 3.

Найдем предел:

2. y= sin x. Вновь воспользуемся определением производной.

3. Аналогично можно показать, что

4. Рассмотрим функцию y= ln x.

5. Используя свойства логарифма можно показать, что

Источник

Дифференцируемость

Оглавление

Действительные функции действительной переменной

Определения

Пояснения

Дифференцируемость следует за непрерывностью : каждая функция, которую можно дифференцировать в одной точке, также непрерывна там. Каждая функция, которую можно дифференцировать в своей области определения, непрерывна. Обратное неверно. Все перечисленные ниже недифференцируемые функции являются непрерывными.

Примеры дифференцируемых функций

Примеры недифференцируемых функций

Поскольку каждая дифференцируемая функция является непрерывной, наоборот, каждая разрывная функция (например, ступенчатая функция или функция Дирихле ) является примером недифференцируемой функции. Но есть также функции, которые непрерывны, но дифференцируемы не везде или не везде.

Корневая функция

Функция суммы

и левая производная

Это типичное поведение для функций, определенных в разделах, где значения функций совпадают на интерфейсах, но не производные. Напротив, графики дифференцируемых функций не имеют изломов.

Третий пример

непрерывна в точке 0, но не дифференцируема (но везде). Следующее относится к коэффициенту разницы в точке 0.

Функция Вейерштрасса

Функция Вейерштрассе названа в честь первооткрывателя

везде постоянна, но нигде не дифференцируема.

Винеровский процесс

Постоянная дифференцируемость и высшие производные

но не является непрерывным в 0.

Сложные функции

Действительные функции нескольких переменных

Частичная дифференцируемость

существует. Итак, вы рассматриваете все переменные, кроме как постоянные, и рассматриваете функцию переменной, полученную таким образом. Икс я <\ displaystyle x_ >

Частичная дифференцируемость не приводит к непрерывности, а только в направлении осей координат.

Производная по направлению

Полная дифференцируемость

Полностью дифференцируемая функция также непрерывна.

В новейшей математической литературе в основном говорят просто о дифференцируемости, а не о полной дифференцируемости. Полная производная также называется дифференциалом.

Связь между различными концепциями дифференцируемости

Инверсии не применяются:

Другое дело, если допустить не только существование, но и непрерывность частных производных.

Поэтому непрерывно частично дифференцируемые функции называют просто непрерывно дифференцируемыми. Здесь тоже не действует обратное:

В целом применимо следующее:

непрерывная частичная дифференцируемость ⇒ полная дифференцируемость ⇒ дифференцируемость по каждому направлению ⇒ частичная дифференцируемость,

однако все обратное неверно.

Примеры

Контрпримеры

Частично дифференцируемые, но не непрерывные и не все производные по направлениям

частично дифференцируема и непрерывна в точке (0,0). Существуют все односторонние производные по направлениям, но кроме координатных направлений, а не двусторонних.

Односторонние, но не двусторонние направленные деривации

Предельное значение существует только с одной стороны, поэтому производные по направлению с обеих сторон не существуют. В частности, функция также не является частично дифференцируемой.

Все производные направления существуют, но не определяют линейное отображение

Здесь существуют все производные по направлениям, для которых применяются частные производные.

Все производные по направлениям существуют и определяют линейное отображение, но не полностью дифференцируемое.

— нулевое отображение, поэтому тривиально линейно.

Полностью дифференцируемый, но не непрерывно частично дифференцируемый

Эта функция моделируется на основе соответствующего примера функции переменной, проверка в основном такая же, как и там.

Отображения между конечномерными векторными пространствами

Функции и отображения в бесконечномерных векторных пространствах

Дифференцируемость по Гато

если предел существует.

Существует несколько несовместимых соглашений для термина дифференцируемость по Гато :

Дифференцируемость по Фреше

Подключения

Дифференцируемые отображения между дифференцируемыми многообразиями

Дифференцируемость образов между дифференцируемыми многообразиями объясняется дифференцируемостью их отображений. Здесь следует исходить из согласованности.

Аналогичным образом определяется комплексная дифференцируемость комплекснозначных функций на комплексных многообразиях и отображений между комплексными многообразиями.

Продление срока

Следующие понятия являются обобщениями дифференцируемости:

Источник