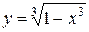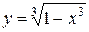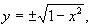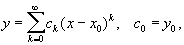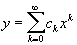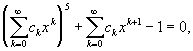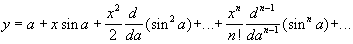что значит неявно заданная функция
СОДЕРЖАНИЕ
Примеры
Обратные функции
Алгебраические функции
Решение для y дает явное решение:
Предостережения
Неявное дифференцирование
В исчислении метод, называемый неявным дифференцированием, использует цепное правило для дифференцирования неявно определенных функций.
Примеры
Пример 1
В качестве альтернативы можно полностью дифференцировать исходное уравнение:
Решение для dy / dx дает
тот же ответ, что и полученный ранее.
Пример 2
Примером неявной функции, для которой неявное дифференцирование проще, чем использование явного дифференцирования, является функция y ( x ), определяемая уравнением
Существенно проще неявно дифференцировать исходное уравнение:
Пример 3
что дает результат
который определен для
Общая формула для производной неявной функции
Теорема о неявной функции
Говоря менее техническим языком, неявные функции существуют и могут быть дифференцированы, если кривая имеет не вертикальную касательную.
В алгебраической геометрии
В дифференциальных уравнениях
Решения дифференциальных уравнений обычно выражаются неявной функцией.
Приложения в экономике
Предельная ставка замещения
Предельная ставка технического замещения
Оптимизация
Неявные функции
Полезное
Смотреть что такое «Неявные функции» в других словарях:
Параметрическое представление функции — Параметрическое представление разновидность представления переменных, когда их зависимость выражается через дополнительную величину параметр. Содержание 1 Параметрическое представление функции 2 Параметрическое представление урав … Википедия
Параметрическое представление — функции, выражение функциональной зависимости между несколькими переменными посредством вспомогательных переменных Параметров. В случае двух переменных х и у зависимость между ними F (х, у) = 0 может быть геометрически истолкована как… … Большая советская энциклопедия
Параметрическое представление — Пример параметрической кривой. Параметрическое представление используемая в математическом анализе разновидность представления переменных, когда их зависимость выражается … Википедия
Еругин, Николай Павлович — [р. 1 (14) мая 1907] сов. математик, акад. АН БССР (с 1956). Чл. КПСС с 1942. В 1932 окончил Лен. ун т. С 1934 преподавал там же (с 1943 проф.). В 1939 41 и 1951 57 работал в Лен. отделении Математич. ин та АН СССР. С 1957 работает в Ин те физики … Большая биографическая энциклопедия
ОПРЕДЕЛЕНИЕ — дефиниция (лат. defenitio ограничение) логическая операция, раскрывающая содержание понятия. Напр., обычное определение термометра указывает, что это, во первых, прибор и, во вторых, именно тот, с помощью которого измеряется температура. Важность … Философская энциклопедия
ЗНАНИЕ НЕЯВНОЕ — скрытое, молчаливое, имплицитное (от лат. implicite в скрытом виде, неявно; противоположное explicite), периферийное в отличие от центрального, или фокального, т.е. находящегося в фокусе сознания. Эмпирич. базис личностного молчаливого… … Энциклопедия культурологии
Разностная схема — Разностная схема это конечная система алгебраических уравнений, поставленная в соответствие какой либо дифференциальной задаче, содержащей дифференциальное уравнение и дополнительные условия (например краевые условия и/или начальное… … Википедия
ОПРЕДЕЛЕНИЕ, — ОПРЕДЕЛЕНИЕ, дефиниция (от лат. «definitio» – «предел», «граница») – логическая процедура придания строго фиксированного смысла терминам языка. Т.к. значения терминов зависят от их смыслов, то всякий раз, придавая через определение какой либо… … Философская энциклопедия
Что значит неявно заданная функция
ПРИМЕР 1. Построение графиков неявных функций одной переменной.
Неявная функция многих переменных. Аналогично рассматривают функции многих переменных, заданные неявно. Например, при выполнении соответствующих условий, уравнение 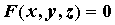
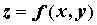
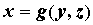
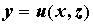
Производная неявной функции. При вычислении производной неявной функции воспользуемся правилом дифференцирования сложной функции. Продифференцируем уравнение 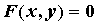
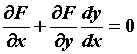
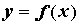
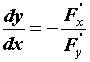
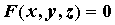
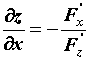
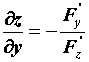
ПРИМЕР 2. Вычисление производных функций, заданных неявно.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Явные и неявные функции
Определение.
Функция называется явной, если она задана формулой, правая часть которой не содержит зависимой переменной.
Такая функция имеет вид: 
Например, 
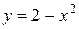

Определение.
Неявной функцией y независимой переменной х называется функция, значения которой находятся из уравнения, связывающего х и y и, не разрешенного относительно y.
Неявная функция имеет вид: 
Например, 

Замечание.
Термины «явная функция» и «неявная функция» характеризуют не природу функции, а способ ее задания.
Основные характеристики функции
Изучить функцию – это значит охарактеризовать ход ее изменения (ее поведение) при изменении независимой переменной. Характеризуют функцию по следующим свойствам:
1) четность или нечетность функции;
2) периодичность функции;
4) возрастание или убывание функции (монотонность функции);
5) ограниченность функции.
Рассмотрим эти характеристики.
Четные и нечетные функции
Определение.
Функция 

Например, 
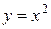

График четной функции расположен симметрично относительно оси 
 |
Определение.
Функция 

Например, 

График нечетной функции расположен симметрично относительно начала координат (рис.1.5).
Функция может быть ни четной. ни нечетной, и в этом случае её называют функцией общего вида.
Например, 


Графики таких функций не симметричны ни относительно оси 
Периодические функции
Определение.
Функция 


Наименьшее из положительных чисел Т, удовлетворяющих условию определения, называется периодом функции 
Например, функции 


Нули функции
Определение.
Значение аргумента, при котором функция обращается в нуль, 
Например, нулями функции 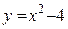


Монотонные функции
Определение.
Функция называется возрастающей (убывающей) в некоторой области изменения аргумента, если большему значению аргумента соответствует большее (меньшее) значение функции (рис.1.6, 1.7).
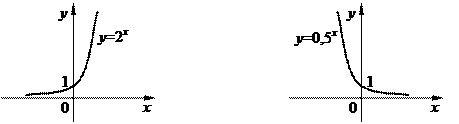 |
Определение.
Если функция в некоторой области изменения аргумента является только возрастающей или только убывающей, то функция называется монотонной.
Ограниченные функции
Определение.
Функция 



Например, функции 




График ограниченной функции лежит между прямыми 

 |
УПРАЖНЕНИЯ
1. Найти область определения следующих функций:
1) 

2) 

3) 

4) 

2. Найти множество значений функции:
1) 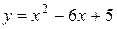

2) 

3) 

3. Найти 




Ответ: 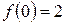


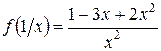
4. Пусть 

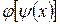

Ответ: 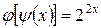

5. Установить чётность или нечётность функции:
1) 
2) 
3) 
4) 
6. Найти основные периоды функций:
1) 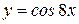

2) 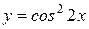
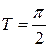
3) 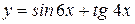

7. Введя промежуточные аргументы, представить данную функцию, как суперпозицию других функций:
1) 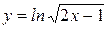


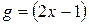
2) 


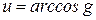


8. Для данных функций найти явные обратные:
1) 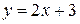

2) 

3)