что значит перпендикулярно в геометрии

13.07.202214.07.2022 admin 0 Comments

Что значит «перпендикулярно»? Происхождение и значение термина

Слово «перпендикулярно» часто встречается в учебниках геометрии. А вот каково происхождение этого понятия? Что значит «перпендикулярно», откуда появилось это слово? Об этом и рассказывается в данной статье.

Происхождение слова

Наречие «перпендикулярно» происходит от существительного «перпендикуляр». Это слово пришло в русский язык из латыни. Там per и pendere означало «перед» и «висеть», а сочетание этих двух слов можно перевести как «отвес». Словосочетание показалось очень удобным, и его стали применять в геометрии.

Перпендикуляром можно назвать прямую. Но не каждую, а лишь ту, которая находится под прямым углом. Поэтому ответ на вопрос о том, что значит перпендикулярно, обязательно должен содержать упоминание прямого угла. Прямая может быть перпендикулярна другой прямой, лучу, вектору, стороне геометрической фигуры и даже плоскости.

Свойства перпендикулярности

Несколько свойств делают перпендикулярность довольно интересным геометрическим явлением. По умолчанию, если первая линия расположена под углом 90° ко второй, то и вторая перпендикулярна первой. Поэтому в условии задачи нет смысла обсуждать, какая из линий перпендикулярна другой.

При изучении высшей математики объяснить, что значит перпендикулярно, будет сложнее. Для математика перпендикулярность – всего лишь частный случай общей математической концепции ортогональности. В понятие перпендикулярности также входит описание многомерных геометрических объектов и их свойств.

Обозначение

На вопрос о том, что значит перпендикулярно, можно ответить и графически. Все математики мира придерживаются определенный условных обозначений, понятных даже тем, кто не знает иностранных языков.

Обозначение перпендикуляра впервые появилось на свет в 1634 году. Оно было опубликовано в работах французского астронома и математика Пьера Эригона. В своем многотомном труде он обобщил все математические знания, известные в то время, и изложил их на французском и латинском языках. Его труды не утратили своего значения много лет спустя – так, Эригона цитировали в своих работах Лейбниц и Паскаль. Он был автором нескольких математических обозначений, наиболее долгоживущим из них оказался знак перпендикулярности. На языке математики «перпендикулярно» выглядит вот так:

Как видно, ничего сложного в обозначении перпендикуляра нет. Просто нужно дорисовать маленький квадратик в углу пересекающихся линий. Иногда перпендикуляр рисуют в виде угла с обозначением в 90°.

Теперь вы тоже знаете о том, что значит слово «перпендикулярно» и кто придумал такое удачное обозначение геометрического понятия.

Источник

Что значит перпендикулярно в геометрии

Углы бывают острые, прямые и тупые.

Угол с градусной мерой 90° называется прямым. Если угол меньше 90°, его называют острым, а если больше 90° — тупым. Угол, равный 180° (то есть образующий прямую линию), называют развёрнутым.

Два угла с одной общей стороной называются смежными.

На рисунке луч ОС делит развёрнутый ∡AOB =180° на две части, образуя тупой ∡1 и острый ∡2.

Поэтому если один из смежных углов прямой, то второй также оказывается прямым: 180° – 90° = 90°

При пересечении двух прямых образуются четыре угла:

Обе стороны ∡1 также являются сторонами ∡3, а стороны ∡2 продолжают стороны ∡4. Такие углы называют вертикальными.

∡1 и ∡2 — смежные, как и ∡1 и ∡4. Следовательно:
∡1 + ∡2 = 180°
∡1 + ∡4 = 180°
∡2 = ∡4

То же справедливо и для ∡1 и ∡3.

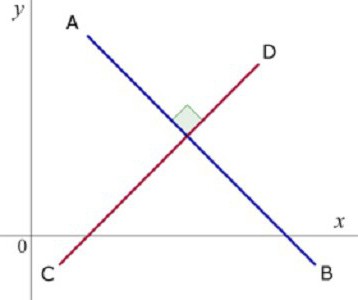
Прямые, пересекающиеся под прямым углом, называются перпендикулярными.

∡1 равен 90°, остальные углы оказываются для него либо смежными, либо вертикальными, а значит, тоже равными 90°.

Перпендикулярность прямых принято обозначать так: a⟂b

Изучайте математику вместе с преподавателями домашней онлайн-школы «Фоксфорда»! По промокоду GEOM72021 вы получите неделю бесплатного доступа к курсу геометрии 7 класса, в котором изучаются перпендикулярные прямые!

Теорема о перпендикулярных прямых

Через каждую точку прямой можно провести перпендикулярную ей прямую, притом только одну.

Построим доказательство теоремы о перпендикулярных прямых «от противного», то есть для начала предположим, что утверждение неверно.

Возьмём прямую a, отметим на ней точки О и B. От луча OB отложим ∡BOA = 90°. Таким образом, отрезок OA будет находиться на прямой, перпендикулярной а.

Теперь предположим, что в той же полуплоскости существует другой перпендикуляр к а, проходящий через О. Назовём его OK. ∡BOK и ∡BOA, равны 90° и лежат в одной полуплоскости относительно луча OB. Но от луча OB в данной полуплоскости можно отложить только один прямой угол. Поэтому другой прямой, проходящей через О и перпендикулярной a, не существует. Теорема доказана.

Свойство перпендикулярных прямых

Две прямые, перпендикулярные третьей, не пересекаются.

Пусть a⟂b и a⟂c. b и с не пересекаются, ведь если бы существовала точка их пересечения, значит, через неё проходили бы две прямые, перпендикулярные a, что невозможно согласно теореме о перпендикулярных прямых. Следовательно, b||с.