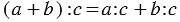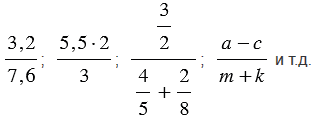что значит представить в виде дроби выражение
Деление и дроби
Не всегда можно одно натуральное число разделить на другое, так, например, 2 нельзя разделить на 3, в таком случае деление можно заменить дробью 

Пример:
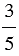
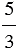
| В результате деления двух натуральных чисел может получится натуральное число или дробное число. |
Пример:
20 : 4 = 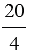
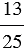
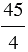
| Всякое натуральное число может быть записано в виде дроби, причем натуральное число можно представить в виде дроби с каким угодно знаменателем. |
Пример:
Получаем, что число 1 можно представить в виде дроби, у которой числитель и знаменатель равны.
Свойство деления суммы на число
Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные частные.
Пример:
(64 + 72) : 8 = 64 : 8 + 72 : 8 = 8 + 9 = 17.
Дробные выражения
| Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением. |
К дробным выражениям относятся:
Обратите внимание, в числителе и в знаменателе дробного выражения могут стоять любые числа (натуральные числа, обыкновенные дроби, десятичные дроби и т.д.), а также числовые или буквенные выражения (смотри примеры выше).
Если числитель и знаменатель дробного выражения разделить или умножить на одно и то же число отличное от нуля, то получим дробное выражение, равное данному. Данное свойство часто используют, когда преобразуют дробное выражение с десятичными дробями в обыкновенную дробь.
Пример:
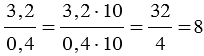
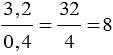
То есть, получается, что мы переносим запятую в числителе и знаменателе дробного выражения на одинаковое количество цифр вправо, при этом если в одном числе цифр после запятой больше, чем в другом, то переносим запятую на большее количество цифр, а там где цифр после запятой меньше дописываем нули.
Пример:
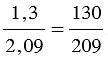
Поделись с друзьями в социальных сетях:
Преобразование рациональных выражений: виды преобразований, примеры
Статья рассказывает о преобразовании рациональных выражений. Рассмотрим виды рациональных выражений, их преобразования, группировки, вынесения за скобки общего множителя. Научимся представлять дробные рациональные выражения в виде рациональных дробей.
Определение и примеры рациональных выражений
Выражения, которые составлены из чисел, переменных, скобок, степеней с действиями сложения, вычитания, умножения, деления с наличием черты дроби, называют рациональными выражениями.
То есть это такие выражения, которые не имеют деления на выражения с переменными. Изучение рациональных выражений начинается с 8 класса, где их называют дробными рациональными выражениями. Особое внимание уделяют дробям в числителе, которые преобразовывают с помощью правил преобразования.
Это позволяет переходить к преобразованию рациональных дробей произвольного вида. Такое выражение может быть рассмотрено как выражение с наличием рациональных дробей и целых выражений со знаками действий.
Основные виды преобразований рациональных выражений
Рациональные выражения используются для того, чтобы выполнять тождественные преобразования, группировки, приведение подобных, выполнение других действий с числами. Цель таких выражений – это упрощение.
Преобразуем в числителе формулу разности квадратов, тогда получаем, что
Представление в виде рациональной дроби
Алгебраическая дробь чаще всего подвергается упрощению при решении. Каждое рациональное приводится к этому разными способами. Необходимо выполнить все необходимые действия с многочленами для того, чтобы рациональное выражение в итоге смогло дать рациональную дробь.
Следует начать с умножения, тогда получим, что
Производим представление полученного результата с исходное. Получим, что
Теперь выполняем вычитание:
После деления придем к рациональной дроби вида
Можно решить это иначе.