что значит провести высоту в треугольнике

Как построить высоту треугольника

Рассмотрим, как построить высоту треугольника с помощью чертежного угольника.

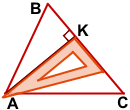
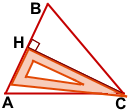
Чтобы построить высоту остроугольного треугольника, надо приложить угольник так, чтобы одна сторона прямого угла проходила через вершину треугольника, а вторая — через противоположную этой вершине сторону.

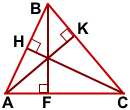
AK — высота треугольника ABC, проведённая из вершины A к противолежащей стороне BC.

BF⊥AC.

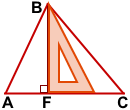
BF — высота треугольника ABC, опущенная из вершины B на сторону AC.

CH — высота треугольника ABC, проведённая из вершины C к стороне AB.

Все высоты треугольника пересекаются в одной точке.

В остроугольном треугольнике точка пересечения высот лежит внутри треугольника.

Если требуется построить все высоты треугольника, достаточно построить две, а третью провести из вершины треугольника через точку пересечения двух высот.

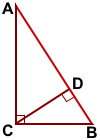
В прямоугольном треугольнике две стороны (катеты) являются также его высотами. Остаётся построить третью высоту.

Угольник прикладываем прямым углом так, чтобы одна сторона проходила через гипотенузу, а другая — через прямой угол.

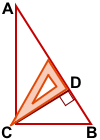
CD — высота прямоугольного треугольника ABC, проведённая из вершины прямого угла C к гипотенузе AB.

Точка пересечения высот прямоугольного треугольника — вершина прямого угла.

Высоты AC, BC и CD прямоугольного треугольника ABC пересекаются в точке C, ∠C=90°.

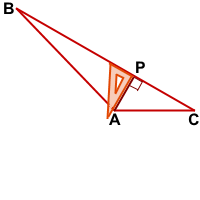
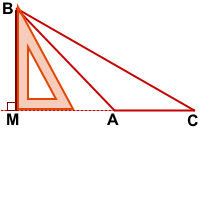
В тупоугольном треугольнике проще всего построить высоту, выходящую из вершины тупого угла.

Прикладываем угольник прямым углом так, чтобы одна его сторона проходила через наибольшую сторону треугольника, а другая — через тупой угол.

AP — высота тупоугольного треугольника ABC, проведённая из вершины тупого угла A к стороне BC.

Только высота, проведённая из вершины тупого угла, лежит внутри треугольника. Две другие высоты находятся вне него.

Высоты тупоугольного треугольника, выходящие из вершин острых углов, проведены не к противолежащим сторонам, а к прямым, содержащим эти стороны.

Чтобы построить высоту, продлеваем противолежащую сторону и прикладываем угольник прямым углом таким образом, чтобы одна сторона угольника проходила через построенную прямую, а другая — через вершину острого угла.

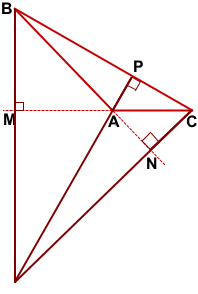
BM — высота тупоугольного треугольника ABC, проведённая из вершины острого угла B к прямой, содержащей противолежащую сторону AC.

CN⊥AB,

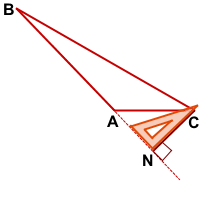
CN — высота тупоугольного треугольника ABC, проведённая из вершины острого угла С к прямой, содержащей противолежащую сторону AB.

Точка пересечения высот тупоугольного треугольника лежит вне него, за тупым углом, напротив наибольшей стороны.

Чтобы построить точку пересечения высот треугольника ABC, продлим прямые BM, CN и AP до пересечения.

Мы рассмотрели, как строить высоты треугольника с помощью угольника.

Построение высот с помощью циркуля и линейки будем рассматривать в теме «Задачи на построение».

Источник

Треугольник. Высота треугольника.

Высота треугольника – перпендикуляр, прочерченный из выбранной вершины треугольника на противолежащею его сторону. Для обозначения высоты треугольника используют букву h, к ней добавляется название той стороны, к которой она прочерчена: h_a, h_b, h_c,

Сторону треугольника, к которой прочерчена высота, называют основанием треугольника.

Высота треугольника может быть прочерчена к любой из трех сторон треугольника. Случается высота треугольника пересекает не само основание треугольника, а его продолжение. Так, высоты AD и ЕМ пересекают продолжения оснований ВС и FK.

Характерные особенности высоты.

В прямоугольном треугольнике высота, прочерченная из вершины прямого угла, разделит его на два треугольника, подобные первоначальному.

В остроугольном треугольнике две его высоты отделяют от него подобные треугольники.

Если треугольник остроугольный, то все основания высот принадлежат его сторонам, а у тупоугольного треугольника две высоты принадлежат продолжению сторон.

Три высоты в остроугольном треугольнике перекрещиваются в одной точке и эту точку обозначают как ортоцентр треугольника.

Источник

Определение и свойства высоты треугольника

В данной публикации мы рассмотрим определение высоты треугольника, продемонстрируем, как она выглядит в зависимости от вида треугольника, а также перечислим ее основные свойства.

Определение высоты треугольника

Высота треугольника – это перпендикуляр, который опущен из вершины фигуры на противоположную сторону.

Основание высоты – точка на противоположной стороне треугольника, которую пересекает высота (или точка пересечения их продолжений).

Обычно высота обозначается буквой h (иногда как h_a – это означает, что она проведена к стороне a).

Высота в разных видах треугольников

В зависимости от вида фигуры высота может:

Свойства высоты треугольника

Свойство 1

Все три высоты в треугольнике (или их продолжения) пересекаются в одной точке, которая называется ортоцентром (точка O на чертежах ниже).

Свойство 2

При пересечении двух высот в треугольнике, образуются следующие подобные треугольники:

Свойство 3

Точка пересечения высот в остроугольном треугольнике является центром окружности, вписанной в его ортотреугольник.

Ортотреугольник – треугольник, вершинами которого являются основания высот △ABC. В нашем случае – это △DEF.

Свойство 4

Точки, которые симметричны ортоцентру треугольника относительно его сторон, лежат на окружности, описанной вокруг этого треугольника.

Примечание: формулы для нахождения высоты треугольника подробно рассмотрены в нашей публикации – “Как найти высоту в треугольнике abc”.

Источник

Высота треугольника (ЕГЭ 2022)

Там, где есть высота, есть и прямой угол.

А значит, и прямоугольный треугольник, который поможет тебе решить массу задач!

И простые подобия, и «хитрые подобия с косинусом», и другие свойства прямоугольных треугольников!

И самое главное – не нужно ничего запоминать.

Научись выводить и никогда не ошибёшься, сможешь всегда себя проверить и решить любую задачу!

Все в этой статье. Читай и смотри видео.

Высота треугольника — коротко о главном

Высота – линия, проведённая из вершины треугольника перпендикулярно противоположной стороне (прямой, которая эту сторону содержит).

Основанием высоты называют ту точку, в которой высота пересекает противоположную сторону (или её продолжение).

Три высоты любого треугольника пересекаются в одной точке.

Высоты треугольника обратно пропорциональны сторонам, на которые они опущены: \( \displaystyle A<_>:B<_>:C<_>=\frac<1>:\frac<1>:\frac<1>\).

Способ 1. Через сторону и угол треугольника: \( \displaystyle A<_>=AC\cdot \sin C=AB\cdot \sin B\).

Способ 3. Через сторону и площадь треугольника: \( \displaystyle A<_>=\frac<2S>\).

Способ 4. Через стороны треугольника и радиус описанной окружности: \( \displaystyle A<_>=\frac<2R>\), где \( \displaystyle R\) — радиус описанной окружности.

Читай далее! Здесь не все…

Высота треугольника — подробнее

Высота – линия, проведённая из вершины треугольника перпендикулярно противоположной стороне (прямой, которая эту сторону содержит).

На этом рисунке \( \displaystyle BH\) – высота.

Но иногда высота (в отличие от биссектрисы и медианы) ведёт себя, как непослушный ребенок – «выбегает» из треугольника. Это бывает в тупоугольном треугольнике.

И тогда получается так:

В общем, не нужно пугаться, если основание высоты оказалось не на стороне треугольника, а «за» треугольником, на продолжении стороны.

Как же решать задачи, в которых участвует высота?

Нужно стремиться применить какие-нибудь знания о прямоугольном треугольнике – ведь где высота – там и прямой угол.

Но попадаются задачи и похитрее, при решении которых лучше обладать дополнительными знаниями заранее, а не выводить их «с нуля». Сейчас мы обсудим некоторые из них.

Но для начала решим простенькую задачку на высоту в тупоугольном треугольнике:

В треугольнике \( \displaystyle ABC\) с тупым углом \( \displaystyle C\) проведена высота \( \displaystyle BH\). Найти \( \displaystyle AC\), если \( AB=2\sqrt<10>\), \( BC=\sqrt<13>\), \( BH=2\).

Смотри: из-за того, что угол \( C\) – тупой, высота \( BH\) опустилась на продолжение стороны \( AC\), а не на саму сторону.

Теперь давай увидим во всём этом два прямоугольных треугольника.

Смотри их целых два:

Применяем теорему Пифагора к треугольнику \( BCH\):

А теперь теорема Пифагора для \( \Delta ABH\):

Теперь осталось только заметить, что \( AC=AH-CH=6-3=3\).

А теперь давай вернемся к нашим высотам!

В треугольнике проведено две высоты

Первый «неожиданный факт»:

Почему бы это? Да очень просто! У них общий угол \( \displaystyle B\) и оба – прямоугольные. Значит, подобны по двум углам.

Второй «неожиданный» факт:

Здесь тоже подобие по двум углам: \( \angle 1=\angle 2\) (как вертикальные) и по прямому углу.

Третий, по-настоящему неожиданный факт:

Вот это уже интереснее, правда? Давай разбираться, почему так.

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

В треугольнике проведены три высоты

Как и для медиан, и для биссектрис, для высот треугольника верно следующее утверждение:

В любом треугольнике три высоты или их продолжения пересекаются в одной точке.

Доказывать это утверждение мы здесь, пожалуй, не будем.

Давай просто нарисуем, чтобы понять, как это бывает «высоты или их продолжения».

1. Треугольник остроугольный – тогда пересекаются сами высоты:

2. Треугольник тупоугольный – тогда пересекаются продолжения высот:

Что же полезного мы ещё не обсудили?

Угол между высотами

Давай узнаем, вдруг угол между высотами можно как–то выразить через углы треугольника? Давай рассмотрим остроугольный треугольник.

Итак, нам хотелось бы найти \( \displaystyle \angle \varphi \).

Смотрим на \( \displaystyle \Delta AHC\). Замечаем, что наш \( \displaystyle \angle \varphi \) – внешний угол в этом треугольнике.

Значит, \( \angle \varphi =\angle 1+\angle 2\).

Чему же равны \( \displaystyle \angle 1\) и \( \displaystyle \angle 2\)?

Но что же это такое? Ведь сумма угла углов треугольника — \( 180<>^\circ \)! Значит, \( \angle \varphi =\angle B\).

Итак, что получилось?

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Остроугольный треугольник и высота

Вернёмся–ка к остроугольному треугольнику. Отметим на рисунке равные углы:

Что видим теперь? Ещё подобные треугольники!

Как от двух линий вообще могут получиться столько подобных треугольников?!

Видишь, какое богатство? И всё это может быть использовано в задачах!

Ну вот, теперь ты узнал что-то новенькое про высоты треугольника.

Теперь пробуй применять в задачах всё это – и соображение о том, что высота образует прямоугольный треугольник, и простые подобия прямоугольных треугольников, получающихся при пересечении двух высот, и подобие похитрее — которое с косинусом, и то, что угол между высотами равен углу между сторонами…

Главное, ты не старался просто запоминать все эти факты, а осознай, что их можно очень просто вывести.

И тогда, если ты будешь точно знать, например, что две проведённые высоты приносят кучу бонусов в виде всяких подобий, то ты непременно и сам получишь все эти бонусы, а заодно – решение своей задачи!

Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике

ЕГЭ №6 Все о равнобедренном треугольнике

Очень часто все «проблемы» с решением задач на равнобедренный треугольник решаются построением высоты.

Очень хороший вебинар, чтобы закрепить решением задач то, что вы изучили в этой статье о высоте.

Вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ. Научимся решать и «обычные» треугольники.

ЕГЭ №6 Все о прямоугольном треугольнике

Важнейшая тема — прямоугольный треугольник — свойства, теорема Пифагора, тригонометрия.

Абсолютное большинство задач геометрии сводятся к прямоугольным треугольникам. Поэтому знать нужно как «Отче наш».

И уметь решать задачи — чем мы займемся на этом вебинаре.

Наши курсы по подготовке к ЕГЭ по математике, информатике и физике

Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны.

Твоя очередь!

Ты знаешь очень много о высоте треугольника. И вот, что нужно сделать дальше. Практикуйся! Ведь я уверен, что с каждой задачей ты будешь все увереннее применять свои знания!

Высота треугольника – не просто перпендикуляр, длину которого мы используем для нахождения площади, верно? Это кое-что покруче 🙂

А теперь мы хотим узнать твое мнение!

Помогла ли тебе эта статья? Понравилась ли она тебе и все ли было понятно?

Напиши внизу в комментариях!

А если остались вопросы, задай их! Мы непременно ответим тебе!

Удачи на экзаменах!

Добавить комментарий Отменить ответ

Один комментарий

Некоторые комментарии прошлых лет к этой статье:

Дарья Сулейманова
15 января 2018
Сидела и готовилась к зачёту по геометрии около двух часов, заходила на множество разных сайтов. И только на вашем сайте всё написано понятным языком, без заумных терминов. Спасибо!

Александр (админ)
15 января 2018
Дарья, спасибо! Всей нашей команде очень приятно это слышать. Мы, консультанты, убеждали математиков использовать «человеческий» язык. И они справились очень хорошо. В результате получилось то, что всем нравится. Мы каждый день получаем благодарности. Еще раз спасибо и удачи на зачете!

Олеся
06 апреля 2018
Готовится с внуком к ОГЭ. Школу закончила 45 лет назад. Учили в то время просто отлично. Многое помню хорошо, но некоторые нюансы забылись. Ваш сайт очень помог. Все лаконично, по существу и без лишних заумных оборотов. Скачала ла себе на телефон. В свободное время просматриваю. С удовольствием решаю задачи. Спасибо Вам.

Александр (админ)
06 апреля 2018
Олеся, спасибо за такой отзыв и удачи Вашему внуку на всех экзаменах. А сайт я лично попросил математиков написать «человеческим языком» ) Судя по отзывам, они справились.

Ольга
15 февраля 2019
А как бы еще доказать подобие треугольников HcHHa и АНС Можно без окружностей

Дмитрий
10 февраля 2020
Скажите, прав ли я. (Задание «Угол между высотами») Что не может угол Фи быть = углу В Так как, угол В это 180 минус угол А+С И угол Н это 180 минус угол А+С Значит В и Н равны, следовательно угол Фи это 180 — Н или минус В, что априори не может быть равным не В не Н.

Алексей Шевчук
13 февраля 2020
Дмитрий, угол H — это угол в треугольнике AHC, но в этом треугольнике углы A и С не равны углам A и C треугольника ABC. Чтобы не возникало такой путаницы, важно (а на экзаменах даже обязательно) писать углы полностью (тремя вершинами): ∠AHC = 180 — (∠HAC + ∠HCA); ∠ABC = 180 — (∠BAC + ∠BCA) — и теперь сразу видно, что это не одно и то же.

Андрей
08 апреля 2020
Очень доходчивый язык учебника. Как в старой советской школе. Я просто в восторге

Александр (админ)
08 апреля 2020
Андрей, спасибо большое! Очень приятно слышать! Сравнение лестное! ))

Источник

Способы нахождения высоты треугольника: теорема и формула

Определение высоты треугольника

Геометрия, являющаяся разделом математики, изучает структуры в пространстве и на плоскости. Одним из типов таких фигур являются геометрические фигуры. К ним можно отнести квадрат, прямоугольник, круг, пятиугольник, треугольник и другие. Из них можно делать более сложные фигуры или оставлять в первоначальном виде.

Треугольником является фигура, относящаяся к классу простых фигур, которая образована тремя точками, находящимися не на одной прямой, и соединенными между собой тремя отрезками.

Треугольники могут быть:

Помимо трех сторон, важными элементами треугольников являются медианы, высоты и биссектрисы.

Высотой треугольника является перпендикуляр, опущенный из угла треугольника вниз, на противоположную сторону.

В геометрии высота треугольника обозначается буквой h.

В зависимости от типа треугольника высота может:

Чтобы сделать высоту графически явной и понятной на рисунке, ее нередко выделяют красной линией.

Для того чтобы определить графическое начертание высоты треугольника, необходимо:

Любой треугольник имеет 3 высоты — по числу углов. Их пересечение находится в точке ортоцентра, которая, в зависимости от типа треугольника, может находиться внутри треугольника, снаружи на пересечении продолжений высот или совпадать с вершиной прямого угла.

Все три высоты треугольника обратно пропорциональны сторонам, к которым опущены. Доказательством будет соотношение:

A × H A ÷ B × H B ÷ C × H C = 1 B C ÷ 1 A C ÷ 1 A B

Выглядеть графически это будет так:

Существует множество способов нахождения высоты треугольника в зависимости от имеющихся данных.

Через площадь и длину стороны, к которой опущена высота:

где S — уже известная площадь треугольника,

Через длины всех сторон:

h = 2 p p × a p × b p × c a

где a, b и c — стороны треугольника,

p — его полупериметр.

Данная формула подходит только для нахождения высоты разностороннего треугольника.

Через длину прилежащей стороны и синус угла:

s i n a — синус угла прилежащей стороны.

Данная формула подходит только для нахождения высоты разностороннего треугольника.

Через стороны и радиус описанной окружности.

Решать задачи с треугольником и описанной окружностью для нахождения высоты можно следующим образом:

где b, c — стороны разностороннего треугольника, к которым не опущена высота,

R — радиус описанной окружности.

Данная формула подходит только для нахождения высоты разностороннего треугольника.

Через длины отрезков, образованных на гипотенузе при проведении к ней высоты треугольника:

где C 1 и С 2 — длины отрезков, образованных на гипотенузе, проведенной к ней высотой.

Данная формула подходит только для нахождения высоты прямоугольного треугольника.

Нахождение высоты равнобедренного треугольника через основание и боковые стороны

Равнобедренным треугольником называют треугольник, имеющий одинаковые по длине катеты, которые образуют равные углы с основанием. В таком треугольнике высота будет опускаться ровно в середину основания, образуя с ним прямой угол.

Помимо высоты, проведенная линия будет являться также осью симметрии, биссектрисой вершинного угла и медианой.

Формула для нахождения высоты в этом случае:

b — равные боковые стороны.

Свойства высоты в равностороннем треугольнике

Равносторонний треугольник — это треугольник, стороны которого, углы, высоты, медианы, оси симметрии и биссектрисы будут равны.

Такой треугольник является частным примером равнобедренного треугольника, но не наоборот.

Высоту в таком треугольнике можно найти с помощью следующей формулы:

где а — сторона равностороннего треугольника.

Главным свойством, которым обладает высота равностороннего треугольника, является тот факт, что она равна медиане и биссектрисе:

а — сторона правильного равностороннего треугольника.

Нахождение высоты прямоугольного треугольника через его катеты

Прямоугольным считается треугольник, у которого один из углов является прямым, то есть равным 90°. Высота, опущенная из такого угла, падает на гипотенузу треугольника и делит его на два прямоугольных треугольника, которые пропорциональны по отношению к большому треугольнику и друг к другу.

Важно отметить, что две другие высоты будут совпадать с катетами треугольника.

Найти высоту в прямоугольном треугольнике, можно через два его катета (a и b) и гипотенузу (c).

Причем гипотенуза также легко находится через катеты по теореме Пифагора:

Расчет высоты идет следующим образом:

где a, b и c — вышеупомянутые стороны треугольника.

Источник