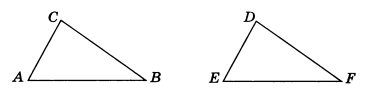что значит соответственно равны в геометрии
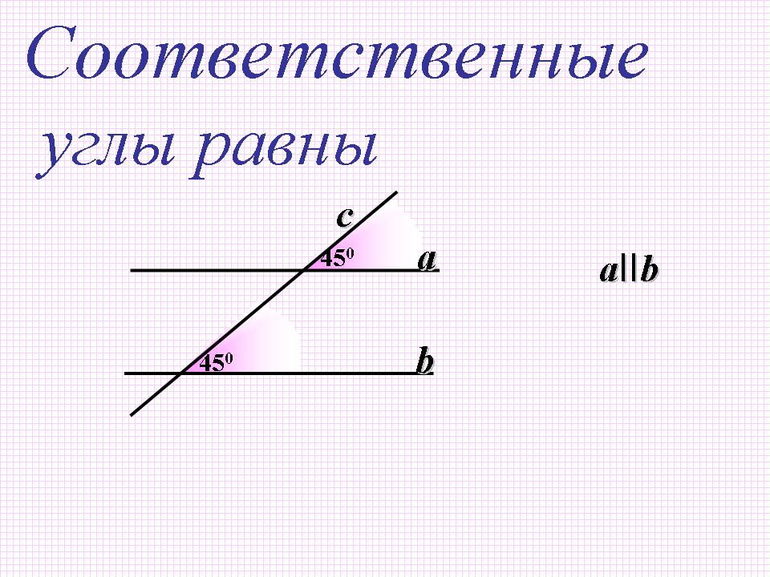
Соответственные углы
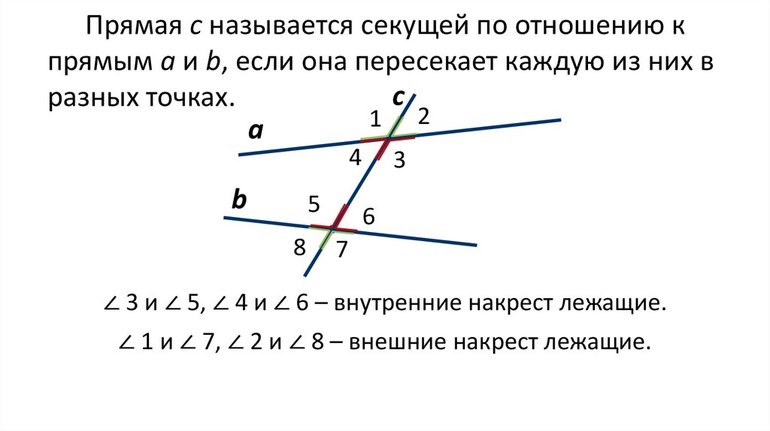
Соответственные углы — вид углов, образованный при пересечении двух прямых секущей.
Один из пары соответственных углов лежит во внутренней области между прямыми, другой — во внешней, причем оба угла находятся по одну сторону от секущей.
При пересечении двух прямых секущей образуется четыре пары соответственных углов.
∠1 и ∠5
∠2 и ∠6
∠3 и∠7
∠4 и ∠8
— соответственные углы при прямых a и b и секущей c.
Наибольший интерес в геометрии представляют соответственные углы при параллельных прямых.
Свойство параллельных прямых
Если две параллельные прямые пересечены третьей прямой, то соответственные углы равны.
∠1 = ∠2
(как соответственные углы при при a ∥ b и секущей c).
Всего при параллельных прямых и секущей образуется четыре пары равных соответственных углов:

∠2 = ∠6
∠3 = ∠7
Признак параллельных прямых
Если соответственные углы равны, то прямые параллельны.

А так как эти углы — соответственные при прямых при a и b и секущей c,
то a ∥ b (по признаку параллельных прямых).
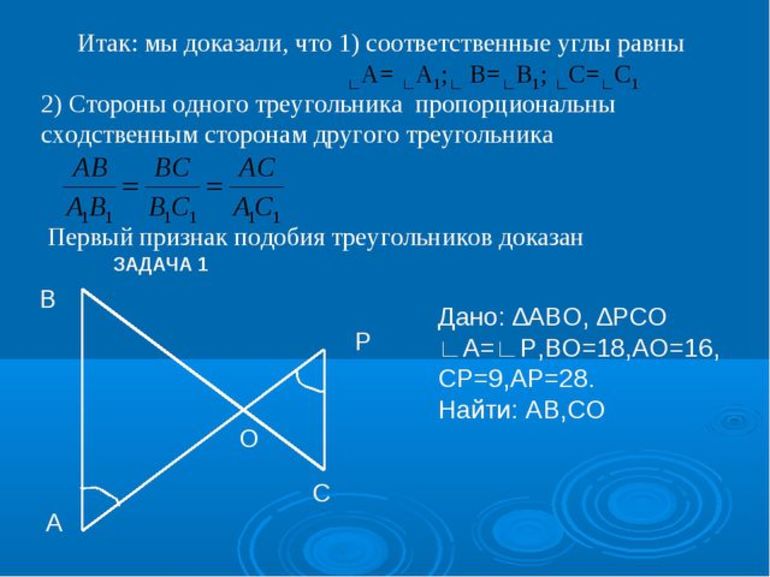
Равенство соответственных углов используется, в частности, для доказательства равенства треугольников и подобия треугольников.
Признаки равенства треугольников
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Первый признак равенства треугольников
Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.
Давайте рассмотрим три признака равенства треугольников.
Теорема 1. Равенство треугольников по двум сторонам и углу между ними.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
При наложении △A1B1C1 на △ABC вершина A1 совмещается с вершиной A, и сторона A1B1 накладывается на сторону AB, AC — на сторону A1C1.
Сторона A1B1 совмещается со стороной AB, вершина B совпадает с вершиной B1, сторона A1С1 совмещается со стороной AС, вершина C совпадает с вершиной C1.
Значит, происходит совмещение вершин В и В1, С и С1.
Второй признак равенства треугольников
Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Путем наложения △ABC на △A1B1C1, совмещаем вершину А с вершиной A1, вершины В и В1 лежат по одну сторону от А1С1.
Тогда АС совмещается с A1C1, вершина C совпадает с C1, поскольку мы знаем, что АС = A1C1.
AB накладывается на A1B1, поскольку мы знаем, что ∠A = ∠A1.
CB накладывается на C1B1, поскольку мы знаем, что ∠C = ∠C1.
Вершина B совпадает с вершиной B1.
Третий признак равенства треугольников
Теорема 3. Равенство треугольников по трем сторонам.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство 3 признака равенства треугольников:
Приложим △ABC к △A1B1C1 таким образом, чтобы вершина A совпала с вершиной A1, вершина B — с вершиной B1, вершина C и вершина C1 лежат по разные стороны от прямой А1В1.
Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.
Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.
Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.
Как понять соответственно равны
СООТВЕ́ТСТВЕННО, нареч. и предлог.
1. нареч. Так, как следует, соответствующим образом. — На два месяца могу вам дать отпуск, если только врачебная комиссия выскажется соответственно. Сергеев-Ценский, Зауряд-полк. Оружием всех видов и родов Приказ [наркома] был соответственно отмечен. Инбер, Пулковский меридиан.
2. предлог с дат. п. Согласно, сообразно чему-л., в зависимости от чего-л. Вечер был великолепный. Поэтическая душа Смычкова стала настраиваться соответственно гармонии окружающего. Чехов, Роман с контрабасом. Овраг вился то влево, то вправо, и ветер соответственно поворотам то утихал, то налетал с удвоенной силой. Казакевич, Сердце друга.
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
СООТВЕ’ТСТВЕННО, нареч. 1. Соответствующим образом, так, как надлежит (надлежало; канц.). Когда получу инструкцию, тогда с. и поступлю. 2. в знач. предлога с дат. п. В соответствии с чем-н., согласно чему-н., в зависимости от чего-н. (книжн.). Поступить с. своим убеждениям. 3. в знач. союза. Также, как; а равно (офиц., канц.). Фруктовые деревья, соответственно и прочие культурные растения, требуют ухода.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
Смотреть что такое «СООТВЕТСТВЕННО» в других словарях:
соответственно — См … Словарь синонимов
Соответственно с — СООТВЕТСТВЕННЫЙ, ая, ое; вен, венна. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
соответственно — (Источник: «Полная акцентуированная парадигма по А. А. Зализняку») … Формы слов
соответственно — предлог, наречие, вводное слово 1. Предлог. Обстоятельственные обороты «соответственно + существительное» могут выделяться знаками препинания (запятыми). Подробнее о факторах, влияющих на расстановку знаков препинания, см. в Приложении 1.… … Словарь-справочник по пунктуации
соответственно — чему и (реже) с чем. Действовать соответственно своему настроению. Поступать соответственно своим убеждениям. Ветер соответственно поворотам то утихал, то налетал в удвоенной силой (Казакевич). Он оглядел меня с ног до головы, прищуривая то один… … Словарь управления
соответственно с — см. соответственно чем. в зн. предлога. Согласно, сообразно чему л., в зависимости от чего л. Поступай соответственно с условиями, с обстоятельствами … Словарь многих выражений
Соответственно Со — предл.; = соответственно с Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
соответственно — соответствующим образом, соответственно устойчивые словосочетания, используемые исключительно для заполнения пустот речи и провалов памяти. (Словарь бизнес сленга компании Schwarzkopf Россия) … Словарь бизнес-сленга
соответственно — I. нареч. 1. Равным образом, в равной мере; тоже, также. Почвы бывают разные, с. различны и способы их обработки. Если ты уедешь завтра, с. уеду и я. 2. Разг. Так, как следует, требуется; надлежащим образом. Узнай решение и поступай с. Будь… … Энциклопедический словарь
соответственно — 1. нареч. 1) Равным образом, в равной мере; тоже, также. Почвы бывают разные, соотве/тственно различны и способы их обработки. Если ты уедешь завтра, соотве/тственно уеду и я. 2) разг. Так, как следует, требуется; надлежащим образом. Узнай… … Словарь многих выражений
Инструменты пользователя
Инструменты сайта
Боковая панель
Геометрия:
Контакты
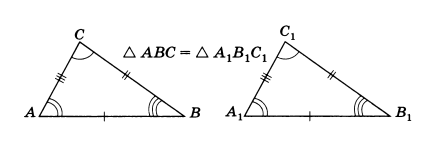
Два треугольника называются равными, если их можно совместить наложением. На рисунке 1 изображены равные треугольники ABC и А1В1С1. Каждый из этих треугольников можно наложить на другой так, что они полностью совместятся, т. е. попарно совместятся их вершины и стороны. Ясно, что при этом совместятся попарно и углы этих треугольников.
Таким образом, если два треугольника равны, то элементы (т. е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Отметим, что в равных треугольниках против соответственно равных сторон (т. е. совмещающихся при наложении) лежат равные углы, и обратно: против соответственно равных углов лежат равные стороны.
Так, например, в равных треугольниках ABC и A1B1C1, изображенных на рисунке 1, против соответственно равных сторон АВ и А1В1 лежат равные углы С и С1. Равенство треугольников ABC и А1В1С1 будем обозначать так: Δ ABC = Δ А1В1С1. Оказывается, что равенство двух треугольников можно установить, сравнивая некоторые их элементы.
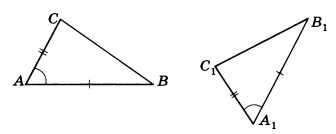
Теорема 1. Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны (рис.2).
Доказательство. Рассмотрим треугольники ABC и A1B1C1, у которых АВ = A1B1, АС = A1C1 ∠ А = ∠ А1 (см. рис.2). Докажем, что Δ ABC = Δ A1B1C1.
Так как ∠ А = ∠ А1, то треугольник ABC можно наложить на треугольник А1В1С1 так, что вершина А совместится с вершиной А1, а стороны АВ и АС наложатся соответственно на лучи А1В1 и A1C1. Поскольку АВ = A1B1, АС = А1С1, то сторона АВ совместится со стороной А1В1 а сторона АС — со стороной А1C1; в частности, совместятся точки В и В1, С и C1. Следовательно, совместятся стороны ВС и В1С1. Итак, треугольники ABC и А1В1С1 полностью совместятся, значит, они равны.
Аналогично методом наложения доказывается теорема 2.
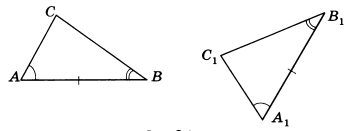
Теорема 2. Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны (рис. 34).
Замечание. На основе теоремы 2 устанавливается теорема 3.
Теорема 3. Сумма любых двух внутренних углов треугольника меньше 180°.
Из последней теоремы вытекает теорема 4.
Теорема 4. Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Теорема 5. Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны (подробнее).
Пример 1. В треугольниках ABC и DEF (рис. 4)
∠ А = ∠ Е, АВ = 20 см, АС = 18 см, DE = 18 см, EF = 20 см. Сравнить треугольники ABC и DEF. Какой угол в треугольнике DEF равен углу В?
Решение. Данные треугольники равны по первому признаку. Угол F треугольника DEF равен углу В треугольника ABC, так как эти углы лежат против соответственно равных сторон DE и АС.
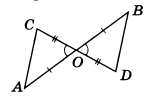
Пример 2. Отрезки АВ и CD (рис. 5) пересекаются в точке О, которая является серединой каждого из них. Чему равен отрезок BD, если отрезок АС равен 6 м?
Решение. Треугольники АОС и BOD равны (по первому признаку): ∠ АОС = ∠ BOD (вертикальные), АО = ОВ, СО = OD (по условию).
Из равенства этих треугольников следует равенство их сторон, т. е. АС = BD. Но так как по условию АС = 6 м, то и BD = 6 м.
Пример 3. В треугольниках ABC и DEF (см. рис. 4) АВ = EF, ∠A = ∠E, ∠B = ∠F.
Сравнить эти треугольники. Какие стороны в треугольнике DEF равны соответственно сторонам ВС и СА?
Решение. Треугольники ABC и DEF равны по второму признаку. Стороны DF и DE треугольника DEF равны соответственно сторонам ВС и СА треугольника ABC, так как стороны DF и ВС (DE и СА) лежат против равных углов Е и A (F и В).
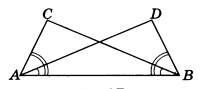
Пример 4. На рисунке 6 углы DAB и СВА, CAB и DBA равны, СА = 13 м. Найти DB.
Решение. Треугольники АСВ и ADB имеют одну общую сторону АВ и по два равных угла, которые прилежат к этой стороне. Следовательно, треугольники АСВ и ADB равны (по второму признаку). Из равенства этих треугольников следует равенство сторон BD и АС, т. е. BD = 13 м.
Как доказать равенство треуголников? Примеры!
Первый признак равенства треугольников
Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Доказательство. Пусть в треугольниках АВС и А 1 В 1 С 1 имеют место равенства
AB= A1B1,
ÐBAC = ÐB1A1C1,
ÐАВС= ÐА1В1С1.
Поступим так же, как и в предыдущем случае. Наложим треугольник А1В1С1 на треугольник АВС так, чтобы совпали стороны AB и A1B1 и прилегающие к ним углы. Как и в предыдущем случае, при необходимости треугольник А1В1С1 можно «перевернуть обратной стороной».
Тогда треугольники совпадут полностью. Значит, они равны.
Третий признак равенства треугольников
Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
Доказательство. Пусть для треугольников ABC и A1B1C1
имеют место равенства АВ = А1В1,
ВС = В1С1,
СА = С1А1.
Перенесем треугольник А1В1С1 так, чтобы сторона А1В1 совпала со стороной АВ, при этом должны совпасть вершины A1 и A, B1 и B.
Рассмотрим две окружности с центрами в A и B и радиусами соответственно AC и BC.
Эти окружности пересекаются в двух симметричных относительно AB точках: C и C2. Значит, точка C1 после переноса указанным образом треугольника A1B1C1 должна совпасть либо с точкой C, либо с точкой C2.
В обоих случаях это будет означать равенство треугольников ABC и A1B1C1, поскольку треугольники ABC и ABC2 равны (эти треугольники симметричны относительно прямой AB.)
Геометрия, Признаки равенства треугольников
Рис. 1
Два треугольника называются равными, если их можно совместить наложением. На рисунке 1 изображены равные треугольники ABC и А1В1С1. Каждый из этих треугольников можно наложить на другой так, что они полностью совместятся, т. е. попарно совместятся их вершины и стороны. Ясно, что при этом совместятся попарно и углы этих треугольников.
Таким образом, если два треугольника равны, то элементы (т. е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Отметим, что в равных треугольниках против соответственно равных сторон (т. е. совмещающихся при наложении) лежат равные углы, и обратно: против соответственно равных углов лежат равные стороны.
Так, например, в равных треугольниках ABC и A1B1C1, изображенных на рисунке 1, против соответственно равных сторон АВ и А1В1 лежат равные углы С и С1. Равенство треугольников ABC и А1В1С1 будем обозначать так: Δ ABC = Δ А1В1С1. Оказывается, что равенство двух треугольников можно установить, сравнивая некоторые их элементы.
Признаки равенства треугольников, геометрия ЕГЭ и ГИА
Рис. 2
Теорема 1. Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны (рис. 2).
Доказательство. Рассмотрим треугольники ABC и A1B1C1, у которых АВ = A1B1, АС = A1C1 ∠ А = ∠ А1 (см. рис. 2). Докажем, что Δ ABC = Δ A1B1C1.
Так как ∠ А = ∠ А1, то треугольник ABC можно наложить на треугольник А1В1С1 так, что вершина А совместится с вершиной А1, а стороны АВ и АС наложатся соответственно на лучи А1В1 и A1C1. Поскольку АВ = A1B1, АС = А1С1, то сторона АВ совместится со стороной А1В1 а сторона АС — со стороной А1C1; в частности, совместятся точки В и В1, С и C1. Следовательно, совместятся стороны ВС и В1С1. Итак, треугольники ABC и А1В1С1 полностью совместятся, значит, они равны.
Аналогично методом наложения доказывается теорема 2.
Признаки равенства треугольников, ГИА, ЕГЭ
Рис. 3
Теорема 2. Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны (рис. 34).
Замечание. На основе теоремы 2 устанавливается теорема 3.
Теорема 3. Сумма любых двух внутренних углов треугольника меньше 180°.
Из последней теоремы вытекает теорема 4.
Теорема 4. Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Теорема 5. Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
Геометрия, Признаки равенства треугольников
Рис. 1
Два треугольника называются равными, если их можно совместить наложением. На рисунке 1 изображены равные треугольники ABC и А1В1С1. Каждый из этих треугольников можно наложить на другой так, что они полностью совместятся, т. е. попарно совместятся их вершины и стороны. Ясно, что при этом совместятся попарно и углы этих треугольников.
Таким образом, если два треугольника равны, то элементы (т. е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Отметим, что в равных треугольниках против соответственно равных сторон (т. е. совмещающихся при наложении) лежат равные углы, и обратно: против соответственно равных углов лежат равные стороны.
Так, например, в равных треугольниках ABC и A1B1C1, изображенных на рисунке 1, против соответственно равных сторон АВ и А1В1 лежат равные углы С и С1. Равенство треугольников ABC и А1В1С1 будем обозначать так: Δ ABC = Δ А1В1С1. Оказывается, что равенство двух треугольников можно установить, сравнивая некоторые их элементы.
Признаки равенства треугольников, геометрия ЕГЭ и ГИА
Рис. 2
Теорема 1. Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны (рис. 2).
Доказательство. Рассмотрим треугольники ABC и A1B1C1, у которых АВ = A1B1, АС = A1C1 ∠ А = ∠ А1 (см. рис. 2). Докажем, что Δ ABC = Δ A1B1C1.
Так как ∠ А = ∠ А1, то треугольник ABC можно наложить на треугольник А1В1С1 так, что вершина А совместится с вершиной А1, а стороны АВ и АС наложатся соответственно на лучи А1В1 и A1C1. Поскольку АВ = A1B1, АС = А1С1, то сторона АВ совместится со стороной А1В1 а сторона АС — со стороной А1C1; в частности, совместятся точки В и В1, С и C1. Следовательно, совместятся стороны ВС и В1С1. Итак, треугольники ABC и А1В1С1 полностью совместятся, значит, они равны.
Аналогично методом наложения доказывается теорема 2.
Признаки равенства треугольников, ГИА, ЕГЭ
Рис. 3
Теорема 2. Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны (рис. 34).
Замечание. На основе теоремы 2 устанавливается теорема 3.
Теорема 3. Сумма любых двух внутренних углов треугольника меньше 180°.
Из последней теоремы вытекает теорема 4.
Теорема 4. Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Теорема 5. Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
Признаки равенства треугольников:
1)По 2 сторонам и углу между ними
Если две стороны и угол между ними одного треугольника
соответственно равны двум сторонам и углу между ними другого
треугольника то такие треугольники равны.
2)По стороне и двум прилежащим к ней углам
Если сторона и два прилежащих к ней угла одного треугольника
соответственно равны стороне и двум прилежащим к ней углам
другого треугольника то такие треугольники равны.
3)По трём сторонам
Если три стороны одного треугольника соответственно равны
трём сторонам другого треугольника то такие треугольники равны.
Базисные понятия
Угол — простая фигура в геометрии, образуемая двумя лучами, следующими из некоторой точки. Эту точку определяют как его вершину. Название «угол» может относиться к части плоскости, объединяющей все лучи, исходящие из вершины фигуры. Такое обозначение может также иметь угловая мера, чаще всего определяемая в градусах.
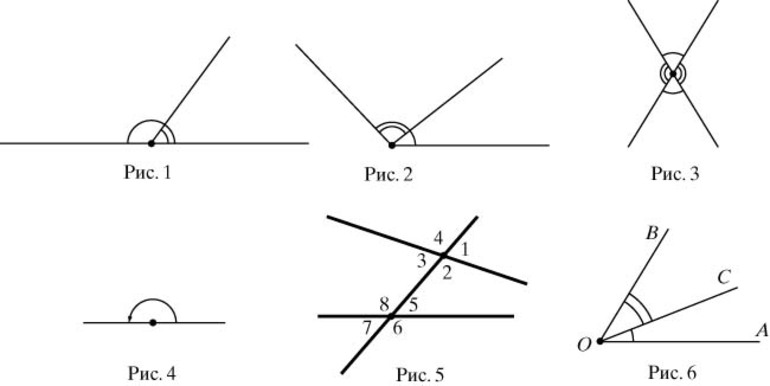
В геометрии существует несколько критериев, позволяющих выделить разные типы угловых фигур. Они бывают тупыми и острыми, смежными или вертикальными. Для углов, образуемых в результате пересечения секущей линией двух прямых, в качестве такого критерия берется свойство взаимных соотношений формируемых при этом фигур. При рассмотрении произвольного геометрического рисунка, образованного двумя прямыми линиями и секущей, можно увидеть 4 пары соответственных, по 2 пары внутренних и внешних накрест лежащих или односторонних угловых фигур. Все эти элементы могут быть как тупоугольными, так и остроугольными.
Углы, образующиеся при пересечении прямых
Чтобы понять, как выглядят соответственные углы, а также уметь находить их на любых геометрических рисунках, нужно хорошо усвоить разницу между типами фигур, образованных секущей линией. Кроме того, следует обратить внимание на наличие внутренней и внешней областей. Первая зона ограничивается площадью между двумя прямыми, второй внешней областью считается неограниченное пространство снаружи от этих двух линий.
Итак, образованным тремя прямыми линиями угловым фигурам можно дать следующие определения:
Более наглядное представление об этом типе углов можно получить, если секущую изобразить в виде направленного вектора. Парные угловые элементы расположены в одном направлении относительно прямых, пересеченных третьей линией.
Чтобы окончательно разобраться в вопросе, нужно усвоить понятие соответствия с математической точки зрения. В геометрии это свойство двух фигур, у которых углы, стороны или точки одного объекта аналогичны соответствующим элементам другого объекта. Аналогия проявляется не в их равенстве, а во взаимном соотношении элементов. О соответствии углов говорит аналогичное пространственное положение лучей в местах пересечения прямых с третьей секущей линией. Таким образом, речь идет об элементах, имеющих одинаковое относительное положение.
Соответственные углы при параллельных прямых
Свойства фигур, формирующихся при пересечении секущей параллельных прямых, давно описаны в планиметрии. Известно, что соответственные накрест лежащие угловые элементы при параллельных прямых равны. Сложение угловых величин односторонних фигур дает значение 180 градусов. В геометрии применяется формула для расчета суммы соответственных парных угловых фигур при условии параллельности двух линий. Для определения этого параметра из числа 360 надо вычесть удвоенную угловую величину одностороннего угла, прилежащего к любому из пары рассчитываемых соответственных угловых элементов.
Равные соответственные углы указывают на параллельность прямых. Справедливость этого признака вытекает из следующих утверждений:
Доказательство можно развернуть и в обратном направлении. Параллельные линии при пересечении третьей прямой формируют одинаковые по величине соответственные углы. Это утверждение известно как свойство параллельных линий.
Такого рода свойства встречаются в описаниях признаков и теорем. Их равенство — часть доказательств равенства и подобия треугольников. В свою очередь, используя признаки подобных и равных треугольников, можно обосновывать доказательства сложных теорем, находить решения сложных задач, править возможные ошибки.
Доказательство подобия треугольников
Существует три признака, по которым могут быть определены подобные треугольники. Во-первых, подобие подтверждается пропорциональностью всех трех сторон треугольников. Во-вторых, подобными считаются треугольники, имеющие две пропорциональные стороны, угловая величина между которыми равна соответствующему элементу второго треугольника. В-третьих, подобие подтверждается, когда имеет место равенство двух углов обоих треугольников.
Рассмотрим доказательство этого признака, в ходе которого применяется свойство тождественности соответственных угловых объектов:
Подобного рода рассуждения и доказательства, учитывающие свойства соответственных угловых фигур, учитываются при решении разного рода задач.
В сложных планиметрических фигурах в качестве секущей, формирующей этот тип геометрических объектов, может выступать медиана, биссектриса треугольника или какие-либо другие линии. Для решения таких задач требуется хорошее знание базовых понятий, признаков, свойств, аксиом, позволяющее заметить определенные соотношения и закономерности в том или ином задании.