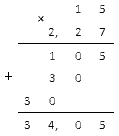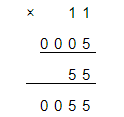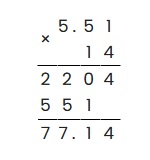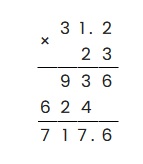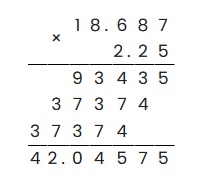что значит умножить десятичную дробь на натуральное число
Что значит умножить десятичную дробь на натуральное число
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
В этом уроке Вы научитесь умножать десятичные дроби на натуральные числа, и узнаете, как можно быстро умножить десятичную дробь на 10, 100, 1000 и т.д.
Для начала давайте решим следующую задачу:
Стоимость одной тетради составляет 12,3 рубля.
Сколько нужно заплатить за три таких тетради?
12,3 + 12,3 + 12,3 = 36,9
Значит 36,9 рубля надо заплатить за эту покупку.
Такую сумму из одинаковых слагаемых называют произведением двенадцати целых трех десятых на натуральное число 3.
Произведением десятичной дроби на натуральное число называют сумму слагаемых, каждое из которых равно этой десятичной дроби, а количество слагаемых равно натуральному числу.
Значение произведения 12,3 на 3 можно найти иначе.
Заметим, что произведение 123 на 3 равно 369, и произведение 12,3 на 3 равно 36,9. Обратим внимание, что после запятой в десятичной дроби стоит один знак, и в полученном произведении после запятой тоже один знак. Мы умножили 12,3 на 3, не обращая внимания на запятую, а затем в полученном произведении отделили запятой справа один знак, потому что в десятичной дроби стоит один знак после запятой.
Таким образом, получили правило:
Чтобы умножить десятичную дробь на натуральное число, нужно:
1: перемножить числа, не обращая внимания на запятую;
2: в полученном произведении справа отделить запятой столько знаков, сколько знаков после запятой находится в десятичной дроби.
Давайте выполним несколько примеров:
1,2 умножить на 6, т.е. 12 умножаем на 6, получаем 72, и справа отделим запятой один знак, получим 7,2.
Другой пример: 0,02 умножить на 15, т.е. 2 умножаем на 15, получится 30, отсчитываем справа два знака и ставим запятую, получится 0,30 или 0,3.
А теперь давайте умножим 1,2 на 10. Получаем 12 умножить на 10, т.е. 120, отделим запятой один знак справа, будет 12,0 или же 12. Заметили, что запятая перескочила на один знак вправо?
А если же 1,234 умножить на 100? Получаем 1234 умножить на 100, будет 123 400, отделим запятой справа три цифры и запишем ответ 123,400 или 123,4. На сколько знаков вправо переместилась запятая после умножения на 100? Правильно, на 2 знака!
В последних примерах мы рассмотрели умножение десятичных дробей на 10 и 100. И увидели закономерность, что запятая переносится вправо на один или два знака. Таким образом, можно сформулировать следующее правило, отличное от правила умножения десятичной дроби на натуральное число.
Чтобы десятичную дробь умножить на 10, 100, 1000 и т.д., необходимо перенести запятую вправо на столько знаков, сколько нулей стоит после единицы. Если же нулей больше, чем знаков после запятой в десятичной дроби, то нужно приписать недостающие нули.
Например: 0,065 умножить на 100, после 1 стоит 2 нуля, значит переносим запятую вправо на 2 знака, получаем 6,5.
Итак, Вы научились умножать десятичную дробь на натуральное число. Как видите, это достаточно просто, нужно перемножить числа и отделить справа запятой столько знаков, сколько их было в десятичной дроби.
А еще Вы теперь знаете, как легко и быстро можно умножать десятичные дроби на 10, 100, 1000 и т. д. с помощью переноса запятой вправо на столько знаков, сколько нулей стоит после 1.
Умножение десятичных дробей: правила, примеры
В данной публикации мы рассмотрим, каким образом десятичную дробь можно умножить на натуральное целое число или другую десятичную дробь. Также разберем примеры для закрепления теоретического материала.
Умножение десятичной дроби на натуральное число
Делитель – 10, 100, 1000, 10000 и т.д.
Чтобы умножить десятичную дробь на натуральное число 10, 100, 1000 и т.д., просто переносим запятую-разделитель вправо на столько нулей, сколько содержит это число.
Пример 1
Объяснение: Т.к. в числе 10 всего один ноль, то и запятую переносим на одну позицию вправо.
Пример 2
Объяснение: Т.к. в числе 100 два нуля, то запятую переносим на две позиции.
Пример 3
Объяснение: В числе 10 один ноль, следовательно, десятичный разделитель сдвигаем на одну позицию.
Пример 4
Объяснение: В числе 1000 три нуля, значит разделитель сдвигаем на три позиции.
Примечание: если количество нулей и, соответственно, позиций переноса разделителя больше, чем цифр после запятой, значит дописываем оставшиеся нули в конце полученного результата. Это работает и в обратную сторону (см. Пример 7 ниже).
Пример 5
Объяснение: В числе 1000 три нуля, следовательно разделитель переносим на две позиции и дописываем один ноль в конце найденного числа.
Делитель – любое число
Чтобы умножить десятичную дробь на любое натуральное целое число, отбрасываем запятую и выполняем умножение, как будто имеем дело не с дробью, а с обычным числом. Затем отсчитываем с конца полученного результата столько цифр, сколько было в дробной части исходной десятичной дроби, и ставим в этом месте запятую.
Пример 6: найдем произведение чисел 5,68 и 8.
Убираем запятую в числе 5,68 и умножаем его на 8:
568 ⋅ 8 = 4544
Отсчитываем две цифры с конца и добавляем запятую-разделитель, т.е.:
Примечание: Если десятичная дробь меньше 1 (т.е. целая часть равна 0), то отбросив запятую, мы не учитываем при умножении ноль/нули, которые идут в начале.
Пример 7: умножим число 0,089 на 7.
Убираем запятую в числе 0,089 и, отбросив нули, умножаем его на 7:
89 ⋅ 7 = 623
Здесь обратная ситуация рассмотренной ранее в Примере 5. С конца отсчитываем 3 цифры, ставим запятую и добавляем ноль слева от нее, т.е.:
Произведение десятичных дробей
Чтобы умножить одну десятичную дробь на другую, выполняем практически те же самые действия, что и описанные в разделе выше – убираем запятые, на этот раз в обеих дробях, и умножаем их как обычные числа. Затем отсчитываем с конца найденного результата столько цифр, сколько их было вместе в дробных частях обоих множителей, и пишем запятую.
Пример 8: найдем, сколько будет 5,615 ⋅ 2,14.
5615 ⋅ 214 = 1201610
Отсчитать с конца нужно 5 цифр, т.к. в первом множителе после запятой было три цифры, во втором – две (5 = 3 + 2). Т.е.:
5,615 ⋅ 2,14 = 12,01610 = 12,0161
Пример 9: вычислим, сколько будет 0,24 ⋅ 3,17.
Отсекаем запятой 4 цифры с конца и получаем ответ – 0,7608.
Правило умножения десятичных дробей на натуральные числа
Умножение десятичных дробей — общие принципы
Десятичная дробь — форма записи обыкновенной дроби, у которой знаменатель равен 10, 100, 1000 и т.д.
Числа со знаменателями 10, 100, 1000 и т.д. записывают без знаменателя. Сначала пишут целую часть, а потом числитель дробной части. Целую часть отделяют от дробной части запятой.
Например, вместо 5 7 10 пишут 5,7 (читают: «5 целых 7 десятых»).
Вместо 3 17 100 пишут 3,17 (читают: «3 целых 17 сотых»).
Десятичные дроби перемножают как целые числа, на запятые внимания не обращают. В результате отделяют запятой столько цифр справа, сколько их стоит после запятой во всех множителях вместе.
Задания подобного плана выполняют по следующему алгоритму:
В двух множителях три цифры после запятой. Нужно отделить три цифры справа в результате и поставить запятую.
Умножение десятичной дроби на обыкновенную дробь или смешанное число
Для того, чтобы умножить десятичную дробь на обыкновенную дробь, необходимо:
Для того, чтобы умножить десятичную дробь на смешанное число, необходимо:
Умножение десятичной дроби на натуральное число
Произведение десятичной дроби и натурального числа — сумма слагаемых, каждое из которых равно этой дроби, а количество слагаемых определяется натуральным числом.
Выражение представляют в виде суммы, в которой слагаемое 0,25 повторяется четыре раза:
Для того, чтобы умножить десятичную дробь на натуральное число, необходимо:
Алгоритм, как ставить запятую, правила переноса
Для того, чтобы в результате умножения правильно поставить запятую, надо:
При умножении десятичной дроби на 10, 100, 1000 и т. д. запятую в десятичной дроби переносят вправо на столько цифр, сколько нулей стоит в множителе после единицы.
Если количество цифр в десятичной дроби после запятой меньше количества нулей после единицы, то нужно:
При умножении десятичной дроби на 0,1; 0,01; 0,001 и т. д. переносят запятую влево на столько цифр, сколько нулей стоит перед единицей в множителе. Нуль целых также учитываем.
Примеры решения задач
Для объяснения решения действуем по алгоритму:
6 5 × 3 4 = 6 × 3 5 × 4 :
Чтобы умножить десятичную дробь на смешанное число:
Решаем пример по схеме:
Запятую в десятичной дроби переносим вправо на две цифры, так как в множителе после единицы стоит два нуля.
Запятую переносим влево на четыре цифры, так как в множителе перед единицей стоит четыре нуля.
Чтобы решить уравнение, нужно найти его корни или доказать, что корней нет.
Для закрепления навыков умножения десятичных дробей используют математические тренажеры.
Умножение десятичных дробей
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
Вернемся к обыкновенным дробям позже, а сейчас обсудим десятичные дроби. Их знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Принципы умножения десятичных дробей
С десятичными дробями можно производить те же действия, что и с любыми другими числами: складывать и вычитать, делить и умножать. В этом блоке узнаем, как умножать дроби.
Умножение десятичных дробей друг на друга можно упростить и просто умножить натуральные числа. Главное — правильно поставить запятую в ответе.
Если в задаче даны десятичные дроби с разными знаками — используем правило умножения отрицательных чисел. Как быстро запомнить:
| «−−» | минус на минус дает плюс |
| «−+» | минус на плюс дает минус |
| «+−» | плюс на минус дает минус |
| «++» | плюс на плюс дает плюс |
Числа с единицей и нулями (10, 100, 1000 и т. д.) называются разрядными единицами, так как цифра 1 — единственная значимая цифра в числе и от ее местоположения зависит количественное значение числа. Важно запомнить правила для умножения и деления на разрядную единицу:
Как умножать десятичные дроби в столбик
Чтобы перемножить десятичные дроби нужно сделать три шага:
Пример 1. Перевести 5,4 в смешанное число.
Как решаем:
Получаем: 311 ∗ 001 = 311.
Ответ: 3,11 ∗ 0,01 = 0,0311.
| Примеры умножения десятичных дробей столбиком: |
|---|
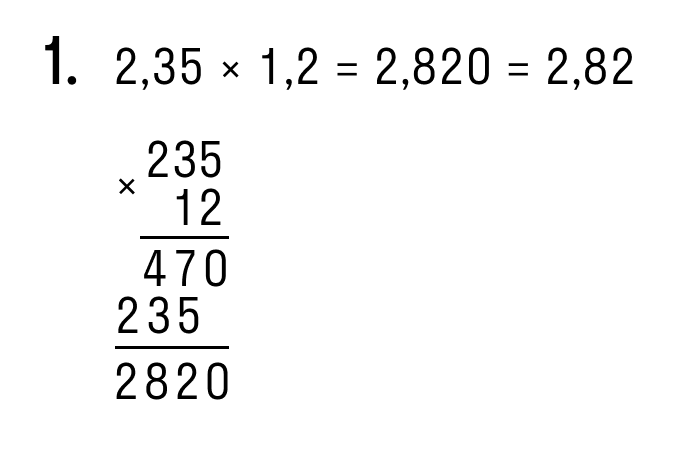 |
 |
 |
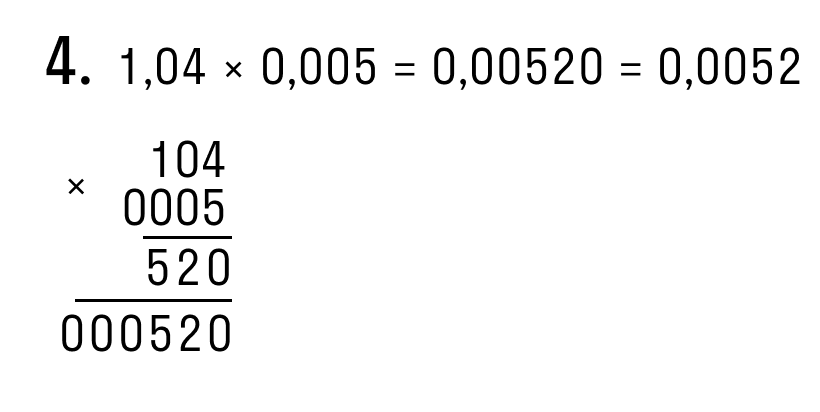 |
Как умножать десятичные дроби на натуральные числа
Умножение десятичных дробей на обычные числа происходит так же, как и умножение между десятичными дробями. Чтобы считать быстрее, умножайте их в столбик по правилам выше. А вот и примерчики!
Пример 1. Умножить десятичную дробь 2,27 на целое число 15.
умножить столбиком данные числа и отделить два знака запятой.
Ответ: 15 ∗ 2,27 = 34,05.
Пример 2. Умножить 11 на 0,005.
умножить столбиком данные числа и отделить три знака запятой.
Ответ: 11 ∗ 0,005 = 0,055.
Пример 3. Умножить 0,1557.. на 3.
Ответ: 0,1557.. ∗ 3 ≈ 0468..
Как умножать десятичные дроби на 10, 100, 1000
Чтобы умножить десятичную дробь на 10, 100, 1000, нужно просто перенести запятую в дроби вправо на столько знаков, сколько нулей стоит во втором множителе. Лишние нули слева можно отбросить. А если цифр не хватает — дописываем нули.
Как умножать десятичные дроби на 0,1, 0,01, 0,001
Чтобы умножить десятичную дробь на 0,1, 0,01, 0,001, нужно перенести запятую в дроби влево на столько знаков, сколько нулей стоит перед единицей. Ноль целых — тоже считаем. Если цифр не хватает — просто дописываем дополнительный ноль — один или несколько — после запятой.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 3/5 на 0,9.
Записать 0,9 в виде обыкновенной дроби:
Пример 2. Умножить 0,18 на 3 1/4.
Записать 3 1/4 в виде десятичной дроби:
Произвести умножение в столбик или при помощи калькулятора:
Ответ: 0,18 ∗ 3 1/4 = 0,585.
А если нужно решить примеры с десятичными дробями быстро — поможет онлайн-калькулятор. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:
Умножение десятичных дробей
Перед тем как перейти к вопросу, о том как умножать десятичные дроби, вспомним теоретические основы. Итак:
Десятичная дробь — это представление обыкновенной дроби в десятичной форме, где знаменатель равен 10, 100, 1000 и т.д. Другими словами, десятичная дробь — это результат деления числителя на знаменатель. К примеру, ½ = 0,5.
Как умножать десятичные дроби?
Умножение десятичных дробей сводится к умножению натуральных чисел, с правильной постановкой запятой. Рассмотрим подробнее основные правила умножения десятичных дробей.
Умножение десятичной дроби на натуральное число
Чтобы умножить десятичную дробь на натуральное число, необходимо:
Пример 1: умножить 5,51 на 14.
Произведем умножение в столбик:
Ответ: 5.51 × 14 = 77.14
Пример 2: умножить 31,2 на 23.
Произведем умножение в столбик:
Ответ: 31.2 × 23 = 717.6
Как умножить две десятичные дроби?
Чтобы перемножить две десятичные дроби, необходимо:
Пример 3: умножить 4,42 на 0,9.
Ответ: 4,42 × 0,9 = 3,978
Пример 4: умножить 18,687 на 2,25.
Ответ: 18,687 × 2,25 = 42,04575
Умножение десятичной дроби на 10 100 1000
Правило умножения десятичной дроби на 10, 100, 1000 и т.д. состоит в том, что для получения ответа, необходимо в этой дроби перенести запятую вправо на столько цифр, сколько нулей в множителе после единицы.
Умножение десятичной дроби на 0,001, 0,01, 0,1?
Правило умножения десятичной дроби на 0,001, 0,01, 0,1 и т.д. состоит в том, что для получения ответа, необходимо в этой дроби перенести запятую влево на столько цифр, сколько нулей в множителе перед единицей.
Как умножить десятичную дробь на обыкновенную?
Для умножения десятичной дроби на обыкновенную, необходимо перевести обыкновенную дробь в десятичную и выполнить умножение по правилу умножения двух десятичных дробей.
Пример: 11.4 умножить на 56/5.