что значит уравнение эйнштейна e mc2

Спросите Итана №78: почему E = mc2?

Самое знаменитое уравнение Эйнштейна вычисляется более красиво, чем это можно было бы ожидать.

Из специальной теории относительности вытекает, что масса и энергия являются разными проявлениями одного и того же – концепция, среднему уму незнакомая.
— Альберт Эйнштейн

Некоторые научные концепции настолько меняют мир и настолько глубоки, что практически каждый знает о них, даже если полностью и не понимает. Почему бы не поработать над этим вместе? Каждую неделю вы отправляете ваши вопросы и предложения, и на этой неделе я выбрал вопрос Марка Лиюва, который спрашивает:

Если бы наша Вселенная не была устроена так, как сейчас, то всё могло бы быть по-другому. Давайте посмотрим, что я имею в виду.

С одной стороны, у нас имеются объекты с массой: от галактик, звёзд и планет до самых мелких молекул, атомов и фундаментальных частиц. Хотя они и крохотные, у каждой из компонент того, что известно нам под именем материи, имеется фундаментальное свойство массы, что означает, что даже если исключить его движение, даже если замедлить его до полной остановки, он всё равно будет оказывать влияние на все остальные объекты Вселенной.

Конкретно, он оказывает гравитационное притяжение на всё остальное во Вселенной, неважно, на каком расстоянии находится удалённый объект. Он притягивает всё к себе, испытывает притяжение ко всему остальному, а также обладает энергией, присущей самому его существованию.

Последнее утверждение контринтуитивно, поскольку об энергии, по крайней мере, в физике, говорят, как о возможности что-либо сделать – о возможности совершать работу. А что можно сделать, если ты просто сидишь на месте?

Перед тем, как ответить, давайте посмотрим на другую сторону монеты – вещи без массы.

С другой стороны, существуют вещи, не имеющие массы – например, свет. У этих частиц есть определённая энергия, и это легко понять, наблюдая их взаимодействие с другими вещами – при поглощении свет передаёт им свою энергию. Свет с достаточной энергией может разогревать материю, добавлять кинетическую энергию (и скорость), вышибать электроны на верхние энергетические уровни или вообще ионизировать, в зависимости от энергии.

Более того, количество энергии, содержащейся в безмассовой частице, определяется только её частотой и длиной волны, произведение которых всегда равняется скорости движения частицы: скорости света. Значит, у более длинных волн частоты меньше, и энергия меньше, а у коротких – частоты и энергия выше. Массивную частицу можно замедлить, а попытки отобрать энергию у безмассовой приведут лишь к удлинению её волны, а не к изменению скорости.

Изначально коробочка не двигается, но поскольку фотоны обладают энергией (и импульсом), когда фотон сталкивается с зеркалом с одной стороны коробки и отскакивает, коробка начнёт движение в том направлении, в котором изначально двигался фотон. Когда фотон достигнет другой стороны, он отразится от зеркала с другой стороны, изменяя импульс коробки обратно до нуля. И он продолжит отражаться таким образом, в то время как коробка половину времени будет двигаться в одну сторону, а другую половину – оставаться неподвижной.

В среднем коробка будет двигаться и, следовательно, так как у неё есть масса, будет иметь определённую кинетическую энергию, благодаря энергии фотона. Но важно также помнить про импульс, количество движения объекта. Импульс фотонов связан с их энергией и длиной волны очень просто: чем короче волна и выше энергия, тем выше импульс.

Подумаем о том, что это значит, и для этого проведём ещё один эксперимент. Представьте, что происходит, когда изначально двигается только сам фотон. У него будет определённое количество энергии и импульс. Оба свойства должны сохраняться, поэтому в начальный момент энергия фотона определена его длиной волны, а у коробки есть только энергия покоя – какая бы она ни была – и фотон обладает всем импульсом системы, а у коробки импульс нулевой.

Затем фотон сталкивается с коробкой и временно поглощается. Импульс и энергия должны сохраняться – это основные законы сохранения Вселенной. Если фотон поглощён, то существует только один способ сохранить импульс – коробка должна двигаться с определённой скоростью в том же направлении, в котором двигался фотон.

Проблема? Нет, это довольно просто решить. Энергия системы коробка/фотон равна массе покоя коробки плюс кинетической энергии коробки плюс энергии фотона. Когда коробка поглощает фотон, большая часть его энергии переходит в увеличение массы коробки. Когда коробка поглотила фотон, её масса меняется (увеличивается) по сравнению с той, что была до столкновения.

Источник

Что означает формула E=mc 2 и как с ее помощью раздобыть много энергии

Игорь Гладкобородов

А то и означает, что масса и энергия — это одно и то же. То есть масса — это частный случай энергии. Энергию, заключенную в массе чего угодно, можно посчитать по этой простой формуле.

Скорость света — это очень много. Это 299 792 458 метров в секунду или, если вам так удобнее, 1 079 252 848,8 километров в час. Из-за этой большой величины получается, что если превратить чайный пакетик целиком в энергию, то этого хватит, чтобы вскипятить 350 миллиардов чайников.

У меня есть пара грамм вещества, где мне получить мою энергию?

Перевести всю массу предмета в энергию можно, только если вы где-нибудь найдете столько же антиматерии. А ее получить в домашних условиях проблематично, этот вариант отпадает.

Термоядерный синтез

Существует очень много природных термоядерных реакторов, вы можете их наблюдать, просто взглянув на небо. Солнце и другие звезды — это и есть гигантские термоядерные реакторы.

Другой способ откусить от материи хоть сколько-то массы и превратить ее в энергию — это произвести термоядерный синтез. Берем два ядра водорода, сталкиваем их, получаем одно ядро гелия. Весь фокус в том, что масса двух ядер водорода немного больше, чем масса одного ядра гелия. Вот эта масса и превращается в энергию.

Но тут тоже не так все просто: ученые еще не научились поддерживать реакцию управляемого ядерного синтеза, промышленный термоядерный реактор фигурирует только в самых оптимистичных планах на середину этого столетия.

Ядерный распад

Ближе к реальности — реакция ядерного распада. Она вовсю используется в ядерных электростанциях. Это когда два больших ядра атома распадаются на два маленьких. При такой реакции масса осколков получается меньше массы ядра, пропавшая масса и уходит в энергию.

Горение

Превращение массы в энергию вы можете наблюдать прямо у вас в руках. Зажгите спичку — и вот она. При некоторых химических реакциях, например, горения, выделяется энергия от потери массы. Но она очень мала по сравнению с реакцией распада ядра, и вместо ядерного взрыва у вас в руках происходит просто горение спички.

Более того, когда вы поели, еда через сложные химические реакции благодаря мизерной потере массы отдает энергию, которую вы потом используете, чтобы сыграть в настольный теннис, ну или на диване перед телеком, чтобы поднять пульт и переключить канал.

Источник

Теория относительности: формула Эйнштейна

Обновлено: 30 Мая 2021

В этой статье речь пойдет о самой знаменитой формуле в мире и о теории, которая лежит во главе современной физической науки. Попробуем рассказать просто о сложном, объясним, что означают основные термины и формулы.

Формула Эйнштейна — краткое описание

Началось все с закона сохранения энергии, который постулирует, что энергия существует всегда и везде, количество ее постоянно, меняется только форма, в которой она проявляется. Закон сохранения массы — это частный случай закона сохранения энергии, согласно которому масса может превращаться в энергию, а энергии соответствует определенная масса.

Каким же образом возможно превращение материи в энергию? Все просто. Что такое излучение? Верно, это энергия. А с другой стороны, излучение — это частицы (материя), которые движутся с огромной скоростью, скоростью света. Таким образом, частица, движущаяся со скоростью света, есть энергия. Частица, находящаяся в состоянии покоя или перемещающаяся медленно — это материя.

Знаменитая формула Эйнштейна как раз описывает преобразование материи в энергию и показывает зависимость материи и энергии от скорости света.

История открытия

В 1905 году немецкий физик Альберт Эйнштейн опубликовал свою специальную теорию относительности. Данная теория описывает движение при скоростях, меньших и близких к скорости света в вакууме.

Основное отличие теории Эйнштейна от классических представлений механики заключается в зависимости пространства и времени от скорости.

В специальной теории относительности Эйнштейном рассматриваются следующие понятия:

Специальная теория относительности позволяет преобразовать пространственно-временные координаты событий при переходе от одной инерциальной системе к другой. Другими словами, она описывает геометрию четырехмерного пространства (куда, помимо привычного нам трехмерного измерения, добавлено время) и основывается на неискривленном или плоском пространстве.

Позже положения специальной теории относительности были применены Эйнштейном к теории гравитации и получили название общей теории относительности.

Предпосылками создания теории относительности послужили 2 причины:

Сам Эйнштейн объяснял свое открытие двумя примерами, которые заставили его задуматься об устройстве пространства-времени и навели на верные мысли:

По другой версии, прозрение пришло к физику одномоментно. Ученый ехал в трамвае и случайно посмотрел на уличные часы. И его внезапно осенила мысль, что если бы трамвай смог разогнаться до скорости света, то в его восприятии уличные часы остановились, и время перестало бы для него существовать. Осознание этого привело его к формулировке одного из постулатов теории: каждый конкретный наблюдатель по-разному воспринимает действительность, включая такие понятия, как расстояние и время.

Влияние формулы

Уравнение Эйнштейна — это основа современной физики. Значение открытия немецкого физика признано величайшим прорывом в физической науке. На основных положениях теории относительности (материя обладает энергией, массу можно преобразовать в энергию) позволили ученым в XX веке совершить следующие открытия:

Как Эйнштейн вывел формулу E=mc²

В 1905 году после публикации статьи «К электродинамике движущихся тел», в которой были сформулированы положения специальной теории относительности, Эйнштейн написал статью «Зависит ли инерция тела от содержащейся в нем энергии?», в которой вывел уравнение E = mc2, опираясь на эффект Доплера.

Эффект Доплера формулируется так:

Длина волны излучения, воспринимаемая наблюдателем, меняется вследствие движения источника излучения и/или движения наблюдателя.

Три составляющие формулы

Несколько сотен лет ученые считали, что масса вещества остается постоянной, независимо от воздействия внешних факторов и реакции с другими веществами. Теория Эйнштейна и главное ее уравнение опровергают это утверждение.

Формула, которая изменила мир: \(E=mc²\) — содержит 3 составляющих:

Из уравнения Эйнштейна следует, что масса и энергия — это разные проявления одного и того же. И зная массу тела, можно рассчитать, чему будет равняться энергия этого тела.

Важнейшие выводы из уравнения

Из уравнения Эйнштейна следуют 3 важнейших следствия:

Общая теория относительности

Альберт Эйнштейн опубликовал специальную теорию относительности в 1905 году. Согласно этой теории, законы природы являются одинаковыми для всех систем отсчета, которые движутся с постоянной скоростью. Общая теория относительности была сформулирована ученым в 1915-1916 гг. Согласно ее положениям, принцип относительности распространяется на любые системы отсчета, независимо от того, движутся они равномерно или с ускорением.

До возникновения общей теории относительности в научном мире считали, что гравитация возникает между объектами, которые обладают массой. Согласно общей теории относительности Эйнштейна, Вселенная состоит из трех пространственных измерений и одного временного, т.е. является четырехмерной. Объекты, обладающие массой, производят искривление в четырехмерном пространстве-времени. А гравитация является следствием этого искривления под воздействием массы. Причем, чем тяжелее тело, тем сильнее пространство-время искривляется под ним и тем сильнее будет его гравитационное поле.

Если следовать положениям общей теории относительности, получается, что сравнительно маленький “шарик” Земля движется вокруг Солнца по конусу воронки, образованной в результате искривления пространства-времени самим тяжелым Солнцем. Сегодня в мире нет лучшего объяснения гравитации, чем то, которое в начале века предложил гениальный физик. Доказательство верности его теории на протяжении последних лет подтверждалось открытиями современных астрофизиков.

Примеры решения уравнения Эйнштейна

Теория относительности Эйнштейна — одна из самых сложных тем в физике. Простой, на первый взгляд, выглядит только формула. Чтобы разобраться в теме досконально, понадобится много времени и помощь людей, которые детально разбираются в этом вопросе. Помните, на образовательном ресурсе Феникс.Хелп помощь готовы оказать только квалифицированные эксперты.

Источник

Учебники

Журнал «Квант»

Общие

Болотовский Б. Простой вывод формулы E = mc 2 //Квант. — 2005. — № 6. — С. 2-7.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Содержание

Введение

Полная и окончательная формулировка современной теории относительности содержится в большой статье Альберта Эйнштейна «К электродинамике движущихся тел», опубликованной в 1905 году. Если говорить об истории создания теории относительности, то у Эйнштейна были предшественники. Отдельные важные вопросы теории исследовались в работах Х.Лоренца, Дж.Лармора, А.Пуанкаре, а также некоторых других физиков. Однако теория относительности как физическая теория до появления работы Эйнштейна не существовала. Работа Эйнштейна отличается от предшествующих работ совершенно новым пониманием как отдельных сторон теории, так и всей теории как целого, таким пониманием, которого не было в работах его предшественников.

Теория относительности заставила пересмотреть многие основные представления физики. Относительность одновременности событий, различия в ходе движущихся и покоящихся часов, отличия в длине движущейся и покоящейся линеек — эти и многие другие следствия теории относительности неразрывно связаны с новыми по сравнению с ньютоновской механикой представлениями о пространстве и времени, а также о взаимной связи пространства и времени.

Одно из важнейших следствий теории относительности — знаменитое соотношение Эйнштейна между массой m покоящегося тела и запасом энергии Е в этом теле:

где с — скорость света.

(Это соотношение называют по-разному. На Западе для него принято название «соотношение эквивалентности между массой и энергией». У нас долгое время было принято более осторожное название «соотношение взаимосвязи между массой и энергией». Сторонники этого более осторожного названия избегают слова «эквивалентность», тождественность, потому что, говорят они, масса и энергия — это разные качества вещества, они могут быть связаны между собой, но не тождественны, не эквивалентны. Мне кажется, что эта осторожность является излишней. Равенство E = mc 2 говорит само за себя. Из него следует, что массу можно измерять в единицах энергии, а энергию — в единицах массы. Кстати, так физики и поступают. А утверждение, что масса и энергия — это разные характеристики вещества, было справедливо в механике Ньютона, а в механике Эйнштейна само соотношение E = mc 2 говорит о тождественности этих двух величин — массы и энергии. Можно, конечно, сказать, что соотношение между массой и энергией не означает их тождественности. Но это все равно, что сказать, глядя на равенство 2 = 2: это не тождество, а соотношение между разными двойками, потому что справа стоит правая двойка, а слева — левая.)

Соотношение (1) обычно выводится из уравнения движения тела в эйнштейновской механике, но этот вывод достаточно труден для ученика средней школы. Поэтому имеет смысл попытаться найти простой вывод этой формулы.

Условие малости скоростей

Мы будем предполагать, что тело массой m, с которым мы будем иметь дело, либо покоится (и тогда, очевидно, скорость его равна нулю), либо, если оно движется, то со скоростью υ, малой по сравнению со скоростью света с. Иными словами, мы будем предполагать, что отношение \(

\frac<\upsilon>\) скорости тела к скорости света есть величина малая по сравнению с единицей. Однако мы будем считать отношение \(

\frac<\upsilon>\) хотя и малой, но не пренебрежимо малой величиной — будем учитывать величины, пропорциональные первой степени отношения \(

\frac<\upsilon>\), но будем пренебрегать вторыми и более высокими степенями этого отношения. Например, если при выводе нам придется иметь дело с выражением \(

\frac<\upsilon^2>\) по сравнению с единицей:

В этом приближении получаются соотношения, которые на первый взгляд могут показаться странными, хотя ничего странного в них нет, надо только помнить, что соотношения эти не являются точными равенствами, а справедливы с точностью до величины \(

\frac<\upsilon>\) включительно, величинами же порядка \(

\frac<\upsilon^2>\) мы пренебрегаем. В таком предположении справедливо, например, следующее приближенное равенство:

Действительно, умножим обе части этого приближенного равенства на \(

т.е. приближенное равенство (2). Поскольку мы считаем, что величина \(

\frac<\upsilon^2>\) пренебрежимо мала в сравнении с единицей, мы видим, что в приближении \(

\frac<\upsilon^2> \ll 1\) равенство (3) справедливо.

Аналогично, нетрудно доказать в том же приближении равенство

Чем меньше величина \(

\frac<\upsilon>\), тем точнее эти приближенные равенства.

Мы не случайно будем использовать приближение малых скоростей. Нередко приходится слышать и читать, что теория относительности должна применяться в случае больших скоростей, когда отношение скорости тела к скорости света имеет порядок единицы, при малых же скоростях применима механика Ньютона. На самом деле теория относительности не сводится к механике Ньютона даже в случае сколь угодно малых скоростей. Мы это увидим, доказав соотношение E = mc 2 для покоящегося или очень медленно движущегося тела. Механика Ньютона такого соотношения дать не может.

Эффект Доплера

Мы начнем с явления, которое называется по имени австрийского физика Кристиана Доплера, открывшего это явление в середине позапрошлого века.

Рассмотрим источник света, причем будем считать, что источник движется вдоль оси x со скоростью υ. Предположим для простоты, что в момент времени t = 0 источник проходит через начало координат, т.е. через точку х = 0. Тогда положение источника в любой момент времени t определяется формулой

Предположим, что далеко впереди излучающего тела на оси x помещен наблюдатель, который следит за движением тела. Ясно, что при таком расположении тело приближается к наблюдателю. Допустим, что наблюдатель взглянул на тело в момент времени t. В этот момент до наблюдателя доходит световой сигнал, излученный телом в более ранний момент времени t’. Очевидно, момент излучения должен предшествовать моменту приема, т.е. должно быть t’ \(

Таким образом, наблюдатель, глядя на движущееся тело в момент времени t, видит это тело там, где оно находилось в более ранний момент времени t’, причем связь между t и t’ определяется формулой (5).

Предположим теперь, что яркость источника периодически меняется по закону косинуса. Обозначим яркость буквой I. Очевидно, I есть функция времени, и мы можем, учитывая это обстоятельство, записать

I = I_0 + I_1 \cos \omega t \ (I_0 > I_1 > 0),\)

где I₀ и I₁ — некоторые постоянные, не зависящие от времени. Неравенство в скобках необходимо потому, что яркость не может быть отрицательной величиной. Но для нас в данном случае это обстоятельство не имеет никакого значения, поскольку в дальнейшем нас будет интересовать только переменная составляющая — второе слагаемое в формуле для I(t).

Пусть наблюдатель смотрит на тело в момент времени t. Как уже было сказано, он видит тело в состоянии, соответствующем более раннему моменту времени t’. Переменная часть яркости в момент t’ пропорциональна cos ωt’. С учетом соотношения (5) получаем

Коэффициент при t под знаком косинуса дает частоту изменения яркости, как ее видит наблюдатель. Обозначим эту частоту через ω’, тогда

Если источник покоится (υ = 0), то ω’ = ω, т.е. наблюдатель воспринимает ту же самую частоту, что излучается источником. Если же источник движется к наблюдателю (в этом случае наблюдатель принимает излучение, направленное вперед по движению источника), то принимаемая частота ω’ отличается от излучаемой частоты ω, причем принимаемая частота больше излучаемой.

Случай, когда источник движется от наблюдателя, можно получить, изменив знак перед υ в соотношении (6). Видно, что тогда принимаемая частота оказывается меньше излучаемой.

Можно сказать, что вперед излучаются большие частоты, а назад — малые (если источник удаляется от наблюдателя, то наблюдатель, очевидно, принимает излучение, испущенное назад).

В несовпадении частоты колебаний источника и частоты, принимаемой наблюдателем, и состоит эффект Доплера. Если наблюдатель находится в системе координат, в которой источник покоится, то излучаемая и принимаемая частоты совпадают. Если же наблюдатель находится в системе координат, в которой источник движется со скоростью υ, то связь излучаемой и принимаемой частот определяется формулой (6). При этом мы предполагаем, что наблюдатель всегда покоится.

Как видно, связь между излучаемой и принимаемой частотами определяется скоростью v относительного движения источника и наблюдателя. В этом смысле безразлично, кто движется — источник приближается к наблюдателю или наблюдатель к источнику. Но нам в дальнейшем удобнее будет считать, что наблюдатель покоится.

Строго говоря, в разных системах координат время течет по-разному. Изменение хода времени также сказывается на величине наблюдаемой частоты. Если,например, частота колебаний маятника в системе координат, где он покоится, равна ω, то в системе координат, где он движется со скоростью υ, частота равна \(

\frac<\upsilon^2>\) по сравнению с единицей, то изменение хода времени для нашего случая (движение с малой скоростью) пренебрежимо мало.

Таким образом, наблюдение за движущимся телом имеет свои особенности. Наблюдатель видит тело не там, где оно находится (пока сигнал идет к наблюдателю, тело успевает переместиться), и принимает сигнал, частота которого ω’ отличается от излучаемой частоты ω.

Выпишем теперь окончательные формулы, которые понадобятся нам в дальнейшем. Если движущийся источник излучает вперед по направлению движения, то частота ω’, принятая наблюдателем, связана с частотой источника ω соотношением

Для излучения назад имеем

Энергия и импульс фотона

Иногда вместо слова «фотон» говорят «квант электромагнитного поля».

Фотон имеет не только энергию, но и импульс, равный

Этих сведений нам будет достаточно для дальнейшего.

Вывод формулы E = mc 2

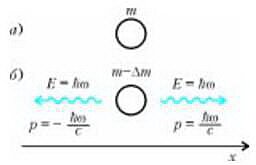
Рассмотрим покоящееся тело массой m. Предположим, что это тело одновременно излучает два фотона в прямо противоположных направлениях. Оба фотона имеют одинаковые частоты ω и, значит, одинаковые энергии \(

E = \hbar \omega\), а также равные по величине и противоположные по направлению импульсы. В результате излучения тело теряет энергию

\Delta E = 2 \hbar \omega. \qquad (9)\)

Потеря импульса равна нулю, и, следовательно, тело после излучения двух квантов остается в покое.

Этот мысленный опыт представлен на рисунке 1. Тело изображено кружком, а фотоны — волнистыми линиями. Один из фотонов излучается в положительном направлении оси x, другой — в отрицательном. Около волнистых линий приведены значения энергии и импульса соответствующих фотонов. Видно, что сумма излученных импульсов равна нулю.

Рассмотрим теперь ту же картину с точки зрения наблюдателя, который движется по оси x влево (т.е. в отрицательном направлении оси x) с малой скоростью υ. Такой наблюдатель увидит уже не покоящееся тело, а тело, движущееся с малой скоростью вправо. Величина этой скорости равна υ, а направлена скорость в положительном направлении оси x. Тогда частота, излучаемая вправо, будет определяться формулой (7) для случая излучения вперед:

\omega’ = \omega \left( 1 + \frac<\upsilon> \right).\)

Мы частоту фотона, излучаемого движущимся телом вперед по направлению движения, обозначили через ω’, чтобы не спутать эту частоту с частотой ω излучаемого фотона в той системе координат, где тело покоится. Соответственно, частота фотона, излучаемого движущимся телом влево, определяется формулой (8) для случая излучения назад:

Чтобы не перепутать излучение вперед и излучение назад, мы будем величины, относящиеся к излучению назад, обозначать двумя штрихами.

Поскольку, из-за эффекта Доплера, частоты излучения вперед и назад различны, энергия и импульс у излученных квантов также будут различаться. Квант, излученный вперед, будет иметь энергию

E’ = \hbar \omega’ = \hbar \omega \left( 1 + \frac<\upsilon> \right)\)

Квант, излученный назад, будет иметь энергию

При этом импульсы квантов направлены в противоположные стороны.

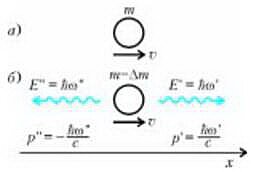
Картина процесса излучения, каким его видит движущийся наблюдатель, изображена на рисунке 2.

Важно здесь подчеркнуть, что на рисунках 1 и 2 изображен один и тот же процесс, но с точки зрения разных наблюдателей. Первый рисунок относится к случаю, когда наблюдатель покоится относительно излучающего тела, а второй — когда наблюдатель движется.

Подсчитаем баланс энергии и импульса для второго случая. Потеря энергии в системе координат, где излучатель имеет скорость υ, равна

т.е. она такая же, как и в системе, где излучатель покоится (см. формулу (9)). Но потеря импульса в системе, где излучатель движется, не равна нулю, в отличие от системы покоя:

Движущийся излучатель теряет импульс \(

\frac<\Delta E \upsilon>\) и, следовательно, должен, казалось бы, тормозиться, уменьшать свою скорость. Но в системе покоя излучение симметрично, излучатель не меняет скорости. Значит, скорость излучателя не может измениться и в той системе, где он движется. А если скорость тела не меняется, то как оно может потерять импульс?

Чтобы ответить на этот вопрос, вспомним, как записывается импульс тела массой m:

\Delta p = \Delta m \upsilon\)

Здесь Δp — изменение импульса тела при неизменной скорости, Δm — изменение его массы.

Это выражение для потери импульса надо приравнять к выражению (10), которое связывает потерю импульса с потерей энергии. Мы получим формулу

\frac<\Delta E>\upsilon = \Delta m \upsilon,\)

\Delta E = \Delta m c^2,\)

которая означает, что изменение энергии тела влечет за собой пропорциональное изменение его массы. Отсюда легко получить соотношение между полной массой тела и полным запасом энергии:

Открытие этой формулы явилось огромным шагом вперед в понимании природных явлений. Само по себе осознание эквивалентности массы и энергии есть великое достижение. Но полученная формула, помимо того, имеет широчайшее поле применения. Распад и слияние атомных ядер, рождение и распад частиц, превращения элементарных частиц одна в другую и множество других явлений требуют для своего объяснения учета формулы связи между массой и энергией.

В заключение — два домашних задания для любителей теории относительности.

\Delta m = \frac<\Delta E>\) для случая системы отсчета, скорость которой υ может быть не малой по сравнению со скоростью света с. Указание. Используйте точную формулу для импульса частицы: \(

Источник