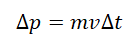что значит закон сохранения импульса
Закон cохранения импульса
9 класс, 10 класс, ЕГЭ/ОГЭ
Импульс: что это такое
Как-то раз Рене Декарт (это который придумал ту самую декартову систему координат) решил, что каждый раз считать силу, чтобы описать процессы — как-то лень и сложно.
Для этого нужно ускорение, а оно не всегда очевидно. Тогда он придумал такую величину, как импульс. Импульс можно охарактеризовать, как количество движения — это произведение массы на скорость.
Импульс тела
→ →
p = mv
p — импульс тела [кг*м/с]
Закон сохранения импульса
В физике и правда ничего не исчезает и не появляется из ниоткуда. Импульс — не исключение. В замкнутой изолированной системе (это та, в которой тела взаимодействуют только друг с другом) закон сохранения импульса звучит так:
Закон сохранения импульса
Векторная сумма импульсов тел в замкнутой системе постоянна
А выглядит — вот так:
Закон сохранения импульса
→ → →
p1 + p2 + … + pn = const
p — импульс тела [кг*м/с]
Простая задачка
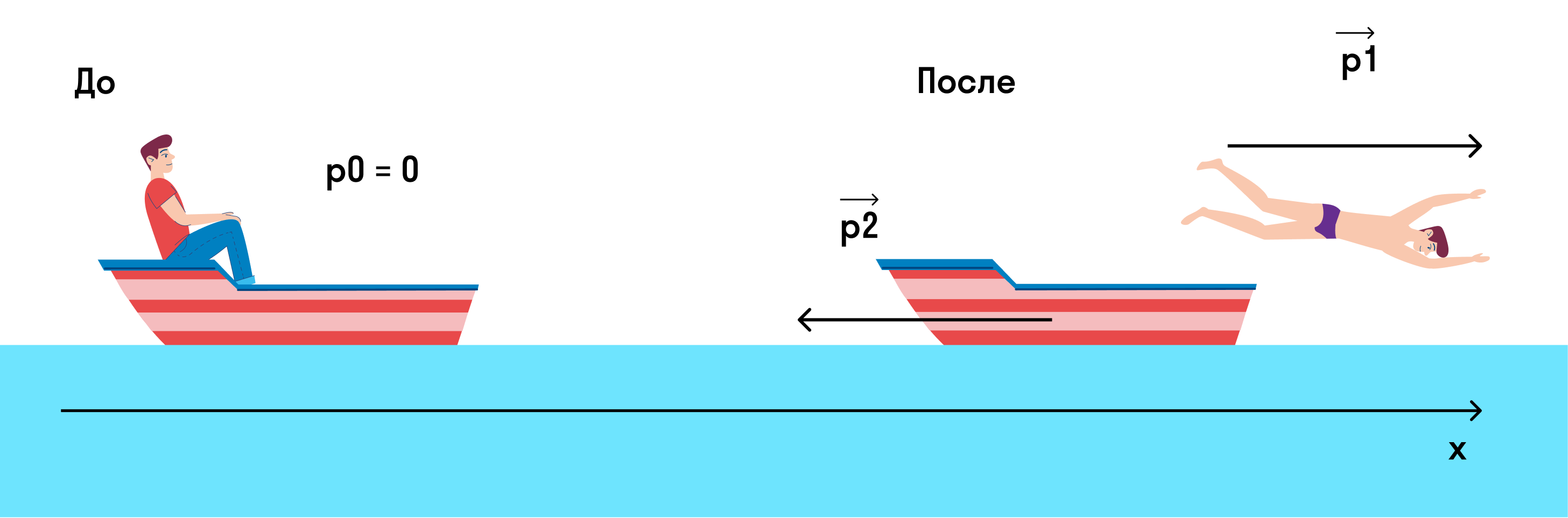
Мальчик массой m = 45 кг плыл на лодке массой M = 270 кг в озере и решил искупаться. Остановил лодку (совсем остановил, чтобы она не двигалась) и спрыгнул с нее с горизонтально направленной скоростью 3 м/с. С какой скоростью станет двигаться лодка?
Решение:
Запишем закон сохранения импульса для данного процесса.
p0 — это импульс системы мальчик + лодка до того, как мальчик спрыгнул,
p1 — это импульс мальчика после прыжка,
p2 — это импульс лодки после прыжка.
Изобразим на рисунке, что происходило до и после прыжка.
Если мы спроецируем импульсы на ось х, то закон сохранения импульса примет вид
0 = p1 — p2
p1 = p2
Подставим формулу импульса.
mV1 = MV2
Выразим скорость лодки V2:
V2 = mV1/M
Подставим значения:
V2 = 45*3/270 = 3/6 = ½ = 0,5 м/с
Ответ: скорость лодки после прыжка равна 0,5 м/с
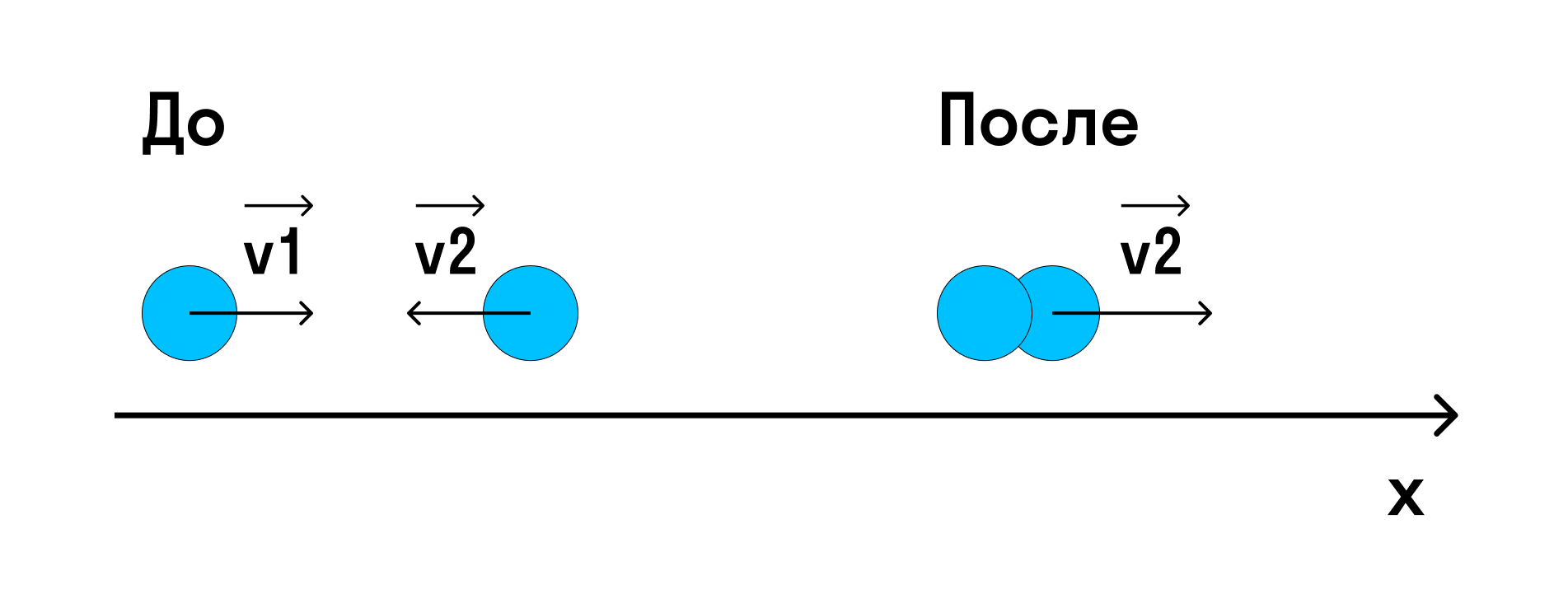
Задачка посложнее
Решение: Для данной системы выполняется закон сохранения импульса:
Импульс системы до удара — это сумма импульсов тел, а после удара — импульс «получившегося» в результате удара тела.
Спроецируем импульсы на ось х:
После неупругого удара получилось одно тело массы m1 + m2, которое движется с искомой скоростью:
m1v1 — mv2 = (m1 + m2) v
Отсюда находим скорость тела, образовавшегося после удара:
v = (m1v1 — mv2)/(m1 + m2)
Переводим массу в килограммы и подставляем значения:
В результате мы получили отрицательное значение скорости. Это значит, что в самом начале на рисунке мы направили скорость после удара неправильно.
Знак минус указывает на то, что слипшиеся тела двигаются в сторону, противоположную оси X. Это никак не влияет на значение получившееся значение.
Ответ: скорость системы тел после соударения равна v = 0,2 м/с.
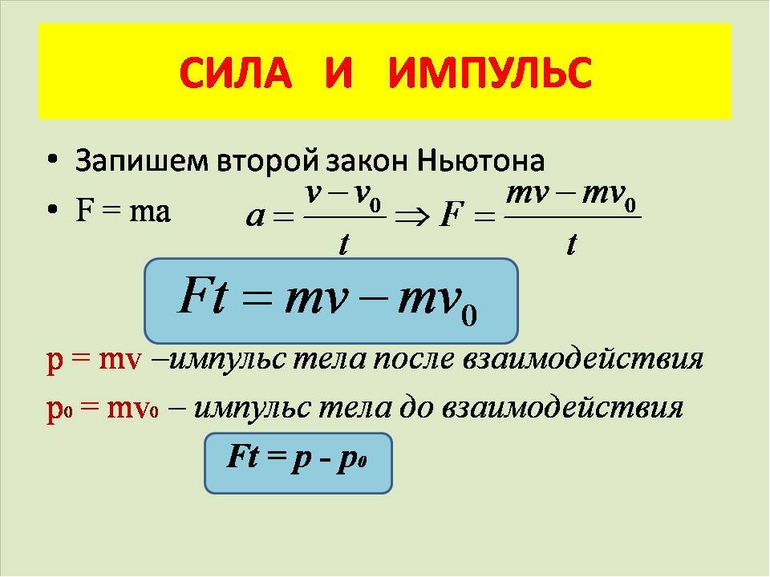
Второй закон Ньютона в импульсной форме
Второй закон Ньютона в импульсной форме можно получить следующим образом. Пусть для определенности векторы скоростей тела и вектор силы направлены вдоль одной прямой линии, т. е. движение прямолинейное.
Запишем второй закон Ньютона, спроецированный на ось х, сонаправленную с направлением движения и ускорением:
Применим выражение для ускорения
Полученное выражение является пропорцией. Применив основное свойство пропорции, получим такое выражение:
В правой части находится Δv =v —v0 — это разница между конечной и начальной скоростью.
Преобразуем правую часть
Раскрыв скобки, получим
Заменим произведение массы и скорости на импульс:
То есть, вектор Δv⋅m – это вектор Δp.
Тогда второй закон Ньютона в импульсной форме запишем так
Вернемся к векторной форме, чтобы данное выражение было справедливо для любого направления вектора ускорения.
Задачка про белку отлично описывает смысл второго закона Ньютона в импульсной форме
Белка с полными лапками орехов сидит на гладком горизонтальном столе. И вот кто-то бесцеремонно толкает ее к краю стола. Белка понимает законы Ньютона и предотвращает падение. Но как?
Решение:
Чтобы к белке приложить силу, которая будет толкать белку в обратном направлении от края стола, нужно создать соответствующий импульс (вот и второй закон Ньютона в импульсной форме подъехал).
Ну, а чтобы создать импульс, белка может выкинуть орехи в сторону направления движения — тогда по закону сохранения импульса ее собственный импульс будет направлен против направления скорости орехов.
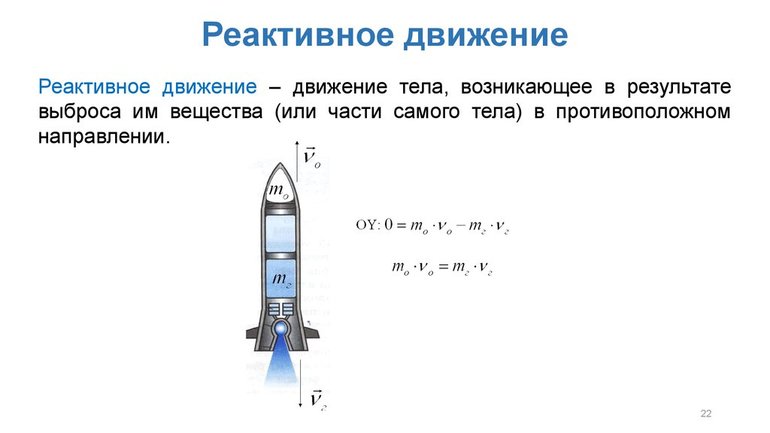
Реактивное движение
В основе движения ракет, салютов и некоторых живых существ: кальмаров, осьминогов, каракатиц и медуз — лежит закон сохранения импульса. В этих случаях движение тела возникает из-за отделения какой-либо его части. Такое движение называется реактивным.
Яркий пример реактивного движения в технике — движение ракеты, когда из нее истекает струя горючего газа, которая образуется при сгорании топлива.
Сила, с которой ракета действует на газы, равна по модулю и противоположна по направлению силе, с которой газы отталкивают от себя ракету:
Сила F2 называется реактивной. Это та сила, которая возникает в процессе отделения части тела. Особенностью реактивной силы является то, что она возникает без взаимодействия с внешними телами.
Закон сохранения импульса позволяет оценить скорость ракеты.
mг vг = mр vр,
где mг — это масса горючего,
vг — скорость горючего,
vр — скорость ракеты.
Отсюда можно выразить скорость ракеты:
Скорость ракеты при реактивном движении
vр = mг vг / mр
mг — это масса горючего [кг]
vг — скорость горючего [м/с]
mр — масса ракеты [кг]
v р — скорость ракеты [м/с]
Эта формула справедлива для случая мгновенного сгорания топлива. Мгновенное сгорание — это теоретическая модель. В реальной жизни топливо сгорает постепенно, так как мгновенное сгорание приводит к взрыву.
Закон сохранения импульса. Реактивное движение
Закон сохранения импульса
Закон сохранения импульса можно наблюдать повсюду. Он достаточно точно выполняется в реальных условиях, если пренебречь сопротивлением воздуха, силами трения и т.д. Примеры проявления этого закона:
Однако, прежде чем говорить о законе сохранении импульса, рассмотрим понятие замкнутой системы.
Формулировка закона сохранения импульса (ЗСИ)
Векторная сумма импульсов всех тел, входящих в замкнутую систему, остается постоянной при любых взаимодействиях этих тел между собой внутри системы.
Данный закон является следствием из второго и третьего законов Ньютона. Покажем это.
По второму закону Ньютона:
Из записанного выше следует соотношение:
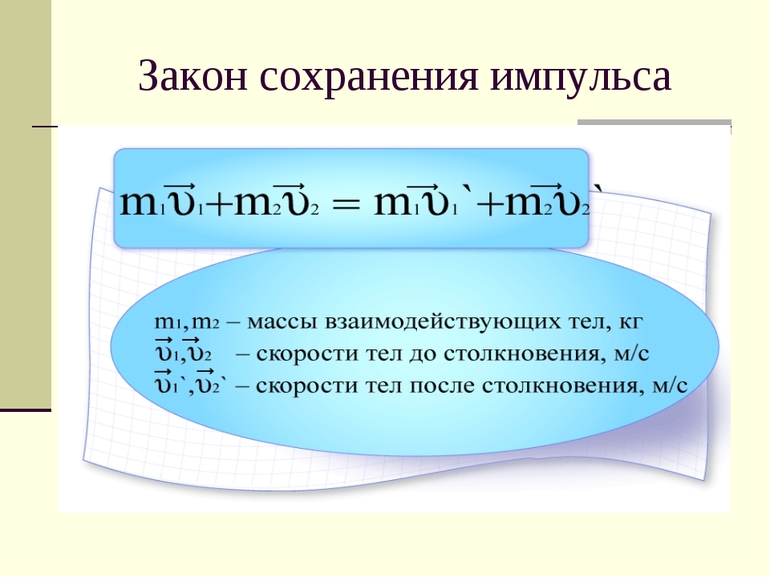
m 1 v 1 → + m 2 v 2 → = m 1 v 1 ‘ → + m 2 v 2 ‘ →
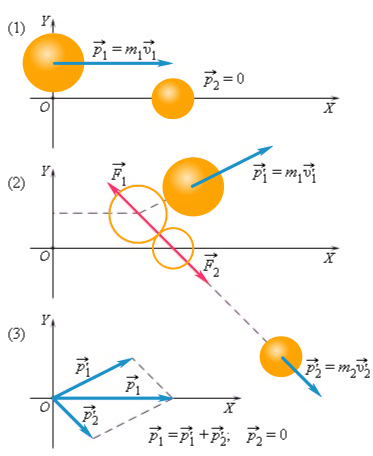
Проиллюстрируем закон сохранения импульса на примере соударения шаров разных масс. Один из шаров до удара покоился.
Как видим, после удара векторная сумма импульсов двух шаров равна первоначальному импульсу движущегося шара.
Важно! Закон сохранения выполняется и для проекций векторов на координатные оси.
Закон сохранения импульса позволяет решать задачи и находить скорости тел не зная значений действующих сил.
По закону сохранения импульса в проекции на ось OX можно записать:
Реактивное движение
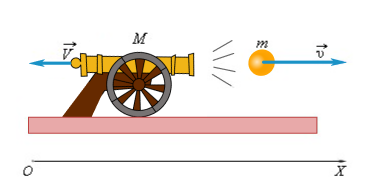
Формула для пушки и снаряда не применима к ракете, так как дает лишь приблизительное представление о движении ракеты, На самом деле вся масса газов выходит из сопла не сразу, а постепенно.
В момент t + ∆ t импульс ракеты равен:
Импульс реактивных газов:
По закону сохранения импульса:
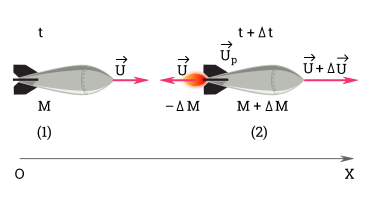
M ∆ v → ∆ t = ∆ M · u → ∆ t ( ∆ t → 0 )
Конечная скорость ракеты определяется по формуле:
Это так называемая формула Циолковского, согласно которой конечная скорость ракеты может превышать скорость истечения газов из сопла двигателя. Правда, достижение такой скорости связано с определенными сложностями. Во-первых, такими, как значительный расход топлива.
Современное ракетостроение развивается в направлении экономичных многоступенчатых ракет. Сброс отсеков с отработанным топливом позволяет значительно сократить массу ракеты и оптимизировать дальнейший расход топлива для ее разгона.
Краткое описание
Импульсом принято называть влияние массы тела на итоговую скорость. На этот случай специалисты разработали следующую формулу: p = m * V. В физике импульс представляет собой некую векторную величину, которая всегда направлена только в одну сторону. Само слово переводится с латинского языка, как «толкать», «двигать». Импульс принято обозначать маленькой буквой р, а вот измеряться он может только в кг*м/с.
Талантливый Рене Декарт был первым человеком, который начал использовать понятие импульс. Он пытался использовать своё открытие как определённую величину, которая заземляет силу. Причина такого подхода Рене весьма очевидна. Измерить единицу силы крайне тяжело, а вот узнать скорость и массу — это задача более простая и выполнимая. Именно поэтому в физике часто говорят, что импульс — это не что другое, как количество движения. Система материальных точек называется замкнутой, если внешние силы отсутствуют, или их равнодействующий показатель равен нулю.
Чтобы можно было разобраться в том, при каких условиях выполняется закон сохранения импульсов, нужно понять, что это физическое направление лежит в основе такого весьма удивительного явления как реактивное движение. Последнее получило широкое применение не только в технике, но и живой природе. Кальмары, осьминоги и медузы отлично используют реактивное движение, которое позволяет им преодолевать большие расстояния в своём подводном мире.
А вот в технике это физическое явление применяется в самолётах, ракетах и даже космических кораблях. Отдельного внимания заслуживает импульс в релятивистской механике. А всё потому, что законы сохранения механической энергии и импульса применяются для решения задач о движении тел после столкновения.
Ключевые особенности
Если применить второй закон Ньютона, то в итоге обязательно получиться вот такое математическое выражение: F1t = m1v1 — m1v1; F2t = m1v2 — m1v2. Для отображения реальной скорости тел в конце взаимодействия используются символы v1 и v2. Из этого можно сделать вывод, что соотношение двух тел будет выглядеть следующим образом: m1v1 + m2v2 = m1v1 + m2v2.
Полученный результат позволяет говорить о равенстве (математическая форма записи закона). Это значит, что первоначальный показатель под воздействием какой-либо силы не изменится. Необходимо запомнить, что определение закона сохранения обязательно выполняется и для проекций векторов на координатные оси. Если следовать всем правилам, то можно легко определить суммарный результат в поставленной задаче, а также находить реальную скорость тел, не зная показателей действующих сил.
На этом примере можно увидеть, что всё элементарно и просто. При движении электронов и других субатомных частиц изменение их состояния происходит скачком без пребывания в промежуточных состояниях. Эту тему активно изучают в 9 классе
Интересные факты
При изучении этой темы нужно понимать, что закон о сохранности импульсов остаётся актуальным исключительно в изолированной/ замкнутой физической системе. В этом случае речь касается той отрасли, где абсолютно все тела тесно взаимодействуют между собой и не реагируют на внешние факторы. Но даже в этом случае действуют свои правила. Лучше представить замкнутую систему, которая состоит из двух физических тел. В этом случае возникают внутренние силы, которые могут характеризоваться определёнными параметрами.
Для первого тела импульс будет равен следующей формуле: Ft = m1v1 — m1v1. В действие снова вступает третий закон Ньютона, описываемый то, что все воздействующие на тела силы равны по своей величине, но противоположны по направлению. А это значит, что для второго тела будет действовать немного другая формула: — Ft = m1v2 — m1v2.
Более точную формулировку закона дали физики, так как они утверждают, что векторная сумма импульсов всех тел в замкнутой системе представляет собой постоянную величину, но только в том случае, воздействующие внешние силы полностью отсутствуют либо векторная сумма была приравнена к нулю. Безусловно, в природе замкнутых систем не существует. Если внешние силы воздействовали на тела в течение короткого промежутка времени, то в такой ситуации можно оставить всё без изменений, а саму систему рассматривать как замкнутую.
Основополагающие моменты
На нашей планете не существует замкнутых систем. Но если суммарные действия внешних сил меньше минимума (к примеру: во время взрыва), то имеющимся воздействием внешних сил предпочитают пренебрегать, из-за чего система приобретает статус замкнутой. Эксперты также придерживаются того мнения, что если воздействие внешних сил всё же присутствует, но итоговая их сумма проекций на одну из координатных осей равна нулю, то в этом направлении закон сохранения образуемых импульсов остаётся актуальным.
Талантливый учёный Исаак Ньютон в своё время изобрёл действительно отличное приспособление, которое как можно лучше демонстрирует сохранность импульса — маятник (колыбель). Это устройство представляет собой небольшую конструкцию, состоящую из 5 одинаковых металлических шаров, каждый из которых прикреплён к каркасу при помощи двух тросов. Основание имеет своеобразную П-образную форму.
Маятник Ньютона построен таким образом, что первый шар передаёт кинетическую энергию второму шарику, а после этого замирает. На первый взгляд, человек может и не заметить, что следующий шар принимает импульс, так как мы не можем проследить его скорость. Но если хорошо присмотреться, то можно увидеть, как шарик немного «вздрагивает» во время столкновения.
Сущность реактивного движения
Это физическое явление тоже основано на принципе отдачи. Из сопла реактивного двигателя предварительно нагретые газы выбрасываются наружу со скоростью n. Масса несгоревшего топлива рана m, а вот вес самой ракеты после истечения газов будет обозначаться большой буквой А. В этом случае пример построен на замкнутой системе под названием «ракета-газ».
Из имеющихся данных может легко определяться скорость ракеты С после истечения газов. Все действия происходят в соответствии с формулой: С= mn /А. Ранее рассмотренная формула для пушки с ядром не является актуальной в этом случае, так как она может дать только приблизительные цифры. Всё дело в том, что основная масса газов выходит из специального сопла не сразу, а постепенно.
В этом случае символом μ μ обозначаем расход задействованного топлива за отведённый промежуток времени. А вот для указания реактивной силы тяги используется сочетание μ u. Направление этой силы максимально совпадает с выбранным направлением движения ракеты. Для расчёта конечной скорости устройства принято использовать формулу: v = nlh (A 0 / A).
Стоит отметить, что
современное ракетостроение шагнуло далеко вперёд, благодаря чему специалисты стремятся развиваться в сторону универсальных многоступенчатых ракет. Своевременный сброс отсеков с уже отработанным топливом позволяет существенно снизить массу агрегата и тем самым максимально оптимизировать дальнейший расход газа для полноценного разгона.
Особенности применения физического явления
Закон сохранения момента импульса весьма удивителен, так как это физическое явление встречается даже в утончённом фигурном катании. А всё дело в том, что раскинув руки в разные стороны и заводя свободную ногу, фигуриста сообщает себе медленное вращение вокруг вертикальной оси. Если резко сгруппироваться, то момент инерции будет снижен, а также произойдёт приращение угловой скорости. Но если ось вращения является свободной, то это не может означать, что в инерциальной системе отсчёта сохраняется прежнее направление угловой скорости.
Способность сохранять созданный импульс занимает в физике почётное место, так как именно на этом понятии построены фундаментальные законы природы. Если следовать теореме Эмми Нётер, то можно понять, что каждому закону обязательно ставится в соответствие определённая симметрия уравнений, описывающих эту систему. Изучаемый закон эквивалентен однородности пространства. Самый элементарный вывод этого утверждения базируется на применении лагранжева подхода.
Импульс тела, закон сохранения импульса
теория по физике 🧲 законы сохранения
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости ( p ↑↓ v ), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p 1отн2— импульс первого тела относительно второго, m1 — масса первого тела, v 1отн2 — скорость первого тела относительно второго, v 1и v 2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
Изменение импульса тела
∆ p — изменение импульса тела, p — конечный импульс тела, p 0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар
Конечный импульс тела:
Модуль изменения импульса тела равен модулю его начального импульса:
Абсолютно упругий удар
Модули конечной и начальной скоростей равны:
Модули конечного и начального импульсов равны:
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:
Пуля пробила стенку
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов:
Радиус-вектор тела повернул на 180 градусов
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали
Модули конечной и начальной скоростей равны:
Модули конечного и начального импульсов равны:
Угол падения равен углу отражения:
Модуль изменения импульса в этом случае определяется формулой:
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
F ∆t — импульс силы, ∆ p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Закон сохранения импульса
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
Отсюда скорость равна:
Импульс частицы до столкновения равен − p 1, а после столкновения равен − p 2, причём p1 = p, p2 = 2p, − p 1⊥ − p 2. Изменение импульса частицы при столкновении Δ − p равняется по модулю:
Алгоритм решения
Решение
Запишем исходные данные:
Δ p = √ p 2 1 + p 2 2
Подставим известные данные:
Δ p = √ p 2 + ( 2 p ) 2 = √ 5 p 2 = p √ 5
pазбирался: Алиса Никитина | обсудить разбор | оценить

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено