Для чего нужны графы в программировании

Зачем студентам теория графов

Ранее я уже писал про приложения теории графов: тут и тут.

В этой статье хочу помочь коллеге в теории графов – он пожаловался в комментарии к своей статье, что:

Здесь я попытался в максимально доступной форме объяснить, как же это делать. И в первую очередь я делаю это для студентов, которые изучают данную тему и могут не понимать, зачем вообще графы нужны. Учась, я лично убедился, что для многих эта тема была «проходной» и они не извлекли из нее никакой ценной информации, а также так и не поняли, как работать с матрицами.

ИМХО для IT-студентов нужно сразу сказать, что списки (стеки, очереди) и бинарные деревья это графы. И всякие схемы, типа схемы метро, автодорог, принципиальные в электронике можно рассматривать как графы. Приложения теории графов — это фундаментальные свойства всяких подобных схем.

Для студентов историков м.б. будет полезно узнать, что фамильные деревья — это графы. И проч. др. специальности. Где только нет графов, пусть на уровне тривиального списка. Возвращаясь к IT: строка символов — граф, и число — последовательность байт — граф, и файл — граф, не говоря о БД.

Дисклеймер. Далее хочу высказать свое сугубо личное мнение, никого ни в чем, не пытаясь убедить или переубедить. Исключительно в порядке обсуждения. Т.о. я адресуюсь к читателям, уже знакомым с теорией графов. Нижеследующее — всего лишь мои предположения. Иногда я опираюсь на факты и на авторитеты (Харари, Зыков, Вирт, Адельсон –Вельский и, как ни странно, А. Дюма), но это не повод тотально засадить всех студентов за зубрежку теории графов в полном объеме.

Вернемся к историкам. Предположим, что ими собрано достаточно документов о том, что у Хуана и Хуаниты, после того, как они сочетались законным браком, было пять детей. Но Хуанита изменяла Хуану и двоих родила внебрачно. А Хуан не остался в долгу и трижды изменил Хуаните – еще двое детей. Однако вопрос: от кого из любовников родила Хуанита?: От Филиппа или от кардинала Ришелье? А может от кого-то из четырех мушкетеров – он была общительной женщиной. Такой вопрос и про Хуана: он был знаком и пользовался расположением королевы Франции, но уделял внимание и ее дамам. (А. Дюма на многих сотнях страниц описывает подобные истории).

Как видим из этого модельного примера — граф (фамильное дерево) можно описать на естественном языке. Но для наглядности его лучше нарисовать, а как будет лучше?
Можно так:

Где черные ребра – документально подтвержденные факты, а красные – предположения.
А можно так: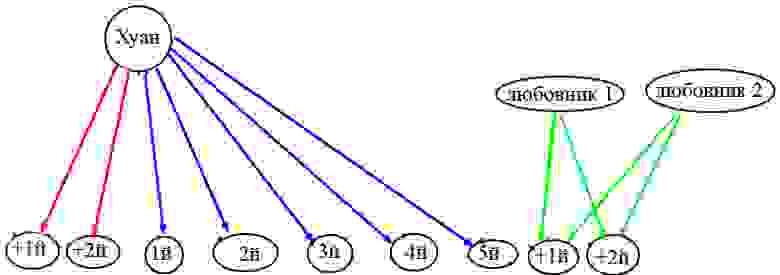

Где красные ребра имеют надпись: «+любовница 1 или + любовница 2 или + любовница 3», т.е. предположения.
Синие и зеленые ребра имеют надпись: «+Хуанита», но синие — документально подтвержденные факты, а зеленые – предположения.

Путь — это результат обхода некоторых вершин графа по правилу: переходить можно только на вершну инцидентную (т.е. связанную ребром) текущей вершине. При этом нельзя возвращаться по уже пройденному ребру.

Цикл – это путь начало, которого и конец, которого в одной и той же вершине.

Это цикл:

И это цикл:

Дерево – это граф без циклов.
Пример:

Линейный список – дерево без ветвей. Т.е. только предыдущий элемент списка всегда инцидентен следующему и никакой другой.

Здесь буквы и пробел – вершины графа, а дефис “-” обозначает ребро.

Г.М. Адельсон-Вельский доказал, что время поиска по дереву зависит от высоты этого дерева. (Н.Вирт в своей знаменитой книге “Алгоритмы + структуры данных = программы” ссылается на эту работу.) Из доказательства Адельсона-Вельского следует, что наихудший случай для дерева – вырождение в линейный список, и, следовательно, превращение списка в достаточно развесистое дерево ускорит поиск.

Для иллюстрации возьмем рекурсивное определение Вирта бинарного дерева.

Рекурсивная процедура сортировки будет такая:

Функция поиска в дереве:

Как сделать развесистое дерево из отсортированного списка – отдельная проблема. Может добавлять в дерево случайным образом, а может использовать алгоритмы балансировки деревьев.

Для гуманитариев может и не нужно вникать в приведенный код. Им важно понять, что список:

Аня
Ваня
Иван Васильевич
и т.д.

не всегда оптимальное решение. Не смогут сами — попросят помочь.

Я (с коллегами) продемонстрировал быстрый поиск при размерности ок.100 лимонов химических соединений (не все реально полученные – некоторые гипотетические). Тут мы встречаемся с важной задачей теории графов – задачей установления изоморфизма двух графов.

Классическая теория графов смотрит только на топологию: какая вершина с какой связаны ребром, а геометрию рисунка не учитывает. Такой подход оказался продуктивным для обобщений и теорем. Но проблема в том, что на листе бумаги мы можем произвольно отметить n точек или кружочков по числу вершин графа, произвольно пронумеровать эти вершины и соединить их линиями, обозначающими ребра. Рисунки одного и того же графа не обязательно совпадут в своей геометрии.

Пример не похожих рисунков:

Кубан – кунеан. Это химическая реакция перехода химического вещества кубан в вещество кунеан. Можно видеть, что структурные формулы органической химии не отличаются от графов.

И этот кунеан на другом рисунке:

Математически в общем случае задача изоморфизма сводится к поиску матрицы перестановки такой, чтобы
A₁= TA₂P,
где A₁ – матрица смежности первого графа;
A₂ – матрица смежности второго графа;
P — матрица перестановки;
T – обратная ( = транспонированная, для данного случая) матрица перестановки.

На словах понятно, что если удается найти для второго графа такую нумерацию, что смежность вершин совпадает с первым (говорят “найти биекцию” — см. Википедию)
к примеру, если в одном графе есть ребро между первой и второй вершинами и в другом графе такое ребро, и так для всех ребер, то графы изоморфны – фактически это один и тот же граф.

Нужно отметить, что для некоторых типов графов задача изоморфизма решается тривиально, для других легко, но для многих требует перебора со сложностью в экспоненту. Тривиально для полных графов – это графы, у которых каждая вершина связана со всеми остальными (инцидентна всем остальным). Понятно, что для любых n вершин существует только один полный граф. Поэтому проверка на изоморфизм сводится к проверке равенства числа вершин первого графа = числу вершин второго. Аналогично для безреберного графа (где только вершины).

Легко задача изоморфизма решается для случая, когда у всех вершин разные степени. Т.к. степени уникальны, то вычисление матрицы перестановки не требуется – простая перенумерация. Каждому номеру вершины второго графа присваиваете номер вершины первого той же степени и проверяете совпадение ребер.

Но не у всех графов степени вершин уникальны. Тут появляются идеи канонической нумерации, т.е. нумерации вершин по жестким однозначным правилам, и полного инварианта графа. Инвариант это обычно (но не обязательно) число, которое не меняется от перенумерации вершин графа. Примером инварианта может служить сумма степеней вершин.
Очевидно, что у двух неизоморфных графов эти инварианты могут совпадать. (Если инварианты не совпадают, то графы точно не изоморфны).

Полные инварианты это, которые, если равны, то графы изоморфны, а если не равны, то не изоморфны. Один из полных инвариантов описан у Зыкова. Матрицу смежности можно развернуть в вектор – нужно просто добавлять в вектор строку за строкой из матрицы. Этот вектор можно рассмотреть, как двоичное число. Можно перебрав все матрицы найти минимальное и максимальное числа. Далее если такие минимальные (или максимальные) числа для двух графов совпадают, то, очевидно, что их матрицы смежности после перестановки будут равны и графы будут изоморфны. К настоящему времени не известен ни один полный инвариант, который можно вычислить без перебора.

Отметим, что изоморфизм деревьев определяется (без полного перебора) с полиномиальной сложностью. А проблема изоморфизма графов остается по-прежнему открытой.

Выше мы затронули проблему отрисовки графов или, как говорят, визуализации. Было предложено много способов (я может, раскачаюсь написать про наиболее полезные), но ни один из них не универсальный. И поэтому графы все рисуют по разному и люди и компьютеры. Я рисую на сделанном мной инструменте.

Возвращаясь к студентам, с которых начал. Думаю, что каждый понимает, что в избранной им области есть структуры. Иногда очень сложные, иногда не очень. Надеюсь мне удалось показать, что теория графов – это теория структур, и учит общим методам обращения со структурами. Может не всем студентам нужно углубляться в эти методы, но понимание общих принципов полезно всем. При этом я не призываю грузить студентов-философов матричной алгеброй – им и так хватает, им положено Платона с Аристотелем читать. Но обзорные лекции будет полезно прослушать со сдачей не сложного зачета, чтобы не прогуливали.

В начале я сказал, что хочу высказать свое сугубо личное мнение, никого не в чем не пытаясь убедить или переубедить. Исключительно в порядке обсуждения. Надеюсь на интересное обсуждение, которое обещает мне много новых знаний о преподавании теории графов для различных специальностей, и о пользе этой теории для этих специальностей.

Источник

5 графов, которые должен знать каждый Data Scientist

Если вы анализируете поведение пользователей, выстраиваете сети или решаете другие динамические задачи, вам не обойтись без структур, которые специально созданы для визуализации взаимоотношений между различными объектами. Речь, разумеется, о графах. Рассказываем про пять разных типов графов: как они применяются в Data Science и как реализованы в Python.

Графы в Python

Граф состоит из отдельных точек (вершин) и соединяющих их линий (ребер). Вершины могут обозначать любые объекты: пользователей сайта, компьютеры корпоративной сети, населенные пункты на карте. Ребра отображают связи между этими объектами: каких пользователей тот или иной человек добавил в друзья, какие компьютеры объединяются прямым подключением, между какими городами проложены дороги. Такая схема позволяет решать множество прикладных задач, и для каждой из них есть много подходящих графов.

Такие структуры гораздо сложнее привычных таблиц баз данных. Представьте себе, что вам нужно создать карту значимых объектов обычного городского района, чтобы понять, где чаще всего бывают его жители. Вам нужно отметить все магазины, школы, МФЦ, и определить вес каждой из точки. Такой код непросто написать с нуля, а полученный результат очень сложно визуализировать в пригодном для работы формате — хаос повседневности формирует очень запутанные связи, даже если мы говорим про район, а не про город или страну.

Всего за 12 месяцев вы пополните портфолио рекомендательной системой, нейронными сетями, выполняющими разные задачи, примете участие в соревнованиях на Kaggle и в хакатонах.

К счастью, Python-программистам не приходится заниматься подготовительной работой. Они могут воспользоваться специальной библиотекой, которая объединяет все необходимые инструменты для создания и анализа графов — NetworkX. Мы также используем этот пакет в следующих примерах.

1. Разбивка вершин на группы

Анализ связных компонентов (connected components) позволяет вам определить внутренние множества внутри вашего графа. Например, вы можете разбить посетителей интернет-магазина на группы по их предпочтениям или географической принадлежности. Или связать между собой подозрительные транзакции в банковской системе, чтобы предположить, что все эти действия провела одна группа мошенников.

Технически алгоритм объединяет в себе два метода, с помощью которых можно найти кратчайший путь между вершинами графа: поиск по ширине (Breadth First Search, BFS) и поиск по глубине (Depth First Search, DFS). Самые старательные ученики Data Science могут подробнее прочитать о них здесь, а мы сразу перейдем к коду.

Допустим, вам нужно распределить города по континентам, используя информацию о расстоянии между ними. Исходный граф выглядит следующим образом:

Сначала мы создаем список граней графа, где расстояния будут использоваться в качестве весов:

edgelist = [[‘Mannheim’, ‘Frankfurt’, 85], [‘Mannheim’, ‘Karlsruhe’, 80], [‘Erfurt’,
‘Wurzburg’, 186], [‘Munchen’, ‘Numberg’, 167], [‘Munchen’, ‘Augsburg’, 84], [‘Munchen’,
‘Kassel’, 502], [‘Numberg’, ‘Stuttgart’, 183], [‘Numberg’, ‘Wurzburg’, 103], [‘Numberg’,
‘Munchen’, 167], [‘Stuttgart’, ‘Numberg’, 183], [‘Augsburg’, ‘Munchen’, 84], [‘Augsburg’,
‘Karlsruhe’, 250], [‘Kassel’, ‘Munchen’, 502], [‘Kassel’, ‘Frankfurt’, 173], [‘Frankfurt’,
‘Mannheim’, 85], [‘Frankfurt’, ‘Wurzburg’, 217], [‘Frankfurt’, ‘Kassel’, 173],
[‘Wurzburg’, ‘Numberg’, 103], [‘Wurzburg’, ‘Erfurt’, 186], [‘Wurzburg’, ‘Frankfurt’, 217],
[‘Karlsruhe’, ‘Mannheim’, 80], [‘Karlsruhe’, ‘Augsburg’, 250],[«Mumbai», «Delhi»,400],
[«Delhi», «Kolkata»,500],[«Kolkata», «Bangalore»,600],[«TX», «NY»,1200],[«ALB», «NY»,800]]

Теперь строим граф с помощью Networkx:

g = nx.Graph()
for edge in edgelist:
g.add_edge(edge[0],edge[1], weight = edge[2])

Остается применить к полученной структуре алгоритм связных компонент:

Готово — мы получили три группы городов, объединенных по континентальному принципу. Эту модель можно применять для самых разных целей. Если бы вместо городов у нас были, например, идентификаторы пользователей, а вместо расстояний — их траты в разных товарных категориях, алгоритм сгруппировал бы их по предпочтениям.

2. Поиск кратчайшего пути

Вычисление наименьшего расстояния между двумя точками — одна из старейших задач программирования. Один из наилучших алгоритмов для ее решения еще в конце 50-х разработал нидерландский математик Эдсгер Дейкстра (Edsger Dijkstra), причем человечество может благодарить за это открытие… его невесту.

Как рассказывал сам Дейкстра, однажды его так утомили походы по магазинам вместе с молодой женой, что во время краткой передышки он задумался — как оптимизировать этот процесс? Буквально за 20 минут он разработал метод, который теперь называется алгоритмом Дейкстры.

Метод прост, как все гениальное. Для начала Data Scientist узнает расстояния от начальной точки до каждой точки в пути. Эти значения присваиваются граням графа. Далее алгоритм поочередно проходит по каждой вершине, на каждом шаге определяя наименьшее расстояние до очередной точки. Когда все точки посещены, вы получаете наименьший маршрут.

По словам самого математика, метод оказался так прост потому, что у него под рукой не было ни клочка бумаги — все калькуляции приходилось вести в голове. Такой способ не дает углубиться в вычисления, поэтому итоговое решение настолько просто, насколько это вообще возможно.

Теперь о том, как алгоритм Дейкстры реализован в Python. Для решения задачи достаточно двух строчек кода:

print(nx.shortest_path(g, ‘Stuttgart’,’Frankfurt’,weight=’weight’))
print(nx.shortest_path_length(g, ‘Stuttgart’,’Frankfurt’,weight=’weight’))
———————————————————
[‘Stuttgart’, ‘Numberg’, ‘Wurzburg’, ‘Frankfurt’]
503

Мы также можем найти кратчайшее расстояние между всеми парами:

for x in nx.all_pairs_dijkstra_path(g,weight=’weight’):
print(x)
———————————————————
(‘Mannheim’, <‘Mannheim’: [‘Mannheim’], ‘Frankfurt’: [‘Mannheim’, ‘Frankfurt’],
‘Karlsruhe’: [‘Mannheim’, ‘Karlsruhe’], ‘Augsburg’: [‘Mannheim’, ‘Karlsruhe’, ‘Augsburg’],
‘Kassel’: [‘Mannheim’, ‘Frankfurt’, ‘Kassel’], ‘Wurzburg’: [‘Mannheim’, ‘Frankfurt’,
‘Wurzburg’], ‘Munchen’: [‘Mannheim’, ‘Karlsruhe’, ‘Augsburg’, ‘Munchen’], ‘Erfurt’:
[‘Mannheim’, ‘Frankfurt’, ‘Wurzburg’, ‘Erfurt’], ‘Numberg’: [‘Mannheim’, ‘Frankfurt’,
‘Wurzburg’, ‘Numberg’], ‘Stuttgart’: [‘Mannheim’, ‘Frankfurt’, ‘Wurzburg’, ‘Numberg’,
‘Stuttgart’]>)
(‘Frankfurt’, <‘Frankfurt’: [‘Frankfurt’], ‘Mannheim’: [‘Frankfurt’, ‘Mannheim’],
‘Kassel’: [‘Frankfurt’, ‘Kassel’], ‘Wurzburg’: [‘Frankfurt’, ‘Wurzburg’], ‘Karlsruhe’:
[‘Frankfurt’, ‘Mannheim’, ‘Karlsruhe’], ‘Augsburg’: [‘Frankfurt’, ‘Mannheim’, ‘Karlsruhe’,
‘Augsburg’], ‘Munchen’: [‘Frankfurt’, ‘Wurzburg’, ‘Numberg’, ‘Munchen’], ‘Erfurt’:
[‘Frankfurt’, ‘Wurzburg’, ‘Erfurt’], ‘Numberg’: [‘Frankfurt’, ‘Wurzburg’, ‘Numberg’],
‘Stuttgart’: [‘Frankfurt’, ‘Wurzburg’, ‘Numberg’, ‘Stuttgart’]>)

В нашем примере мы определили маршруты между городами, но этот же метод можно использовать и для выстраивания связей между пользователями соцсети, и для планирования оптимального маршрута покупателя в торговом зале, и для любых прочих подобных проблем.

Вы пополните свое портфолио десятком решенных задач и кейсов. Опыт работы с данными позволит вам быстрее сориентироваться в программе и использовать ресурсы карьерного центра для быстрого развития карьеры.

3. Поиск оптимального пути

Всем знакомы головоломки, в которых нужно начертить какую-либо фигуру, не проходя дважды через одну точку. В профессии Data Scientist такие задачи возникают, когда нужно проложить оптимальный путь для кабеля, помочь торговым представителям или мастерам по обслуживанию банкоматов спланировать маршрут, и так далее.

В каждом случае помогает алгоритм минимального остовного дерева (Minimum Spanning Tree). Этот термин обозначает подграф, который объединяет ребра с минимально возможной суммой весов. Это не всегда означает, что одна вершина не может иметь больше двух ребер — главное значение имеет итоговая сумма их значений.

Чтобы построить такую структуру, используйте команду nx.minimum_spanning_tree(g):

4. Рейтинг вершин графа

Еще одна нередкая задача — найти, какие вершины имеют самое важное значение в рамках того или иного явления. Например, поисковики определяют вес разных интернет-страниц, академики считают, какие научные работы чаще всего ссылаются исследователи, социальные сети отслеживают пользователей с наибольшим количеством подписок.

На примере социальных сетей мы и рассмотрим метод. Достаем из хранилища данных список пользователей Facebook:

fb = nx.read_edgelist(‘../input/facebook-combined.txt’, create_using = nx.Graph(),
nodetype = int)

pos = nx.spring_layout(fb)
import warnings
warnings.filterwarnings(‘ignore’)
plt.style.use(‘fivethirtyeight’)
plt.rcParams[‘figure.figsize’] = (20, 15)
plt.axis(‘off’)
nx.draw_networkx(fb, pos, with_labels = False, node_size = 35)
plt.show()

Теперь посмотрим, у каких пользователей наибольшее влияние. Алгоритм Pagerank умеет сам это делать, опираясь на количество онлайн-друзей:

pageranks = nx.pagerank(fb)
print(pageranks)
——————————————————
<0: 0.006289602618466542,
1: 0.00023590202311540972,
2: 0.00020310565091694562,
3: 0.00022552359869430617,
4: 0.00023849264701222462,
……..>

Чтобы узнать пользователей с наибольшим весом, мы используем этот код:

import operator
sorted_pagerank = sorted(pageranks.items(), key=operator.itemgetter(1),reverse = True) print(sorted_pagerank)
——————————————————
[(3437, 0.007614586844749603), (107, 0.006936420955866114), (1684, 0.0063671621383068295),
(0, 0.006289602618466542), (1912, 0.0038769716008844974), (348, 0.0023480969727805783), (686, 0.0022193592598000193), (3980, 0.002170323579009993), (414, 0.0018002990470702262),
(698, 0.0013171153138368807), (483, 0.0012974283300616082), (3830, 0.0011844348977671688),
(376, 0.0009014073664792464), (2047, 0.000841029154597401), (56, 0.0008039024292749443), (25, 0.000800412660519768), (828, 0.0007886905420662135), (322, 0.0007867992190291396),……]

А чтобы определить «самого крутого парня», можно построить подграф:

first_degree_connected_nodes = list(fb.neighbors(3437))
second_degree_connected_nodes = []
for x in first_degree_connected_nodes: second_degree_connected_nodes+=list(fb.neighbors(x)) second_degree_connected_nodes.remove(3437)
second_degree_connected_nodes = list(set(second_degree_connected_nodes)) subgraph_3437 = nx.subgraph(fb,first_degree_connected_nodes+second_degree_connected_nodes)
pos = nx.spring_layout(subgraph_3437)
node_color = [‘yellow’ if v == 3437 else ‘red’ for v in subgraph_3437]
node_size = [1000 if v == 3437 else 35 for v in subgraph_3437]
plt.style.use(‘fivethirtyeight’)
plt.rcParams[‘figure.figsize’] = (20, 15)
plt.axis(‘off’) nx.draw_networkx(subgraph_3437, pos, with_labels = False, node_color=node_color,node_size=node_size )
plt.show()

5. Центральность вершин

Понятие центральности обозначает расстояние какой-либо вершины графа до его центра. Измерение центральности — это еще один способ определить влияние разных участников базы данных.

В отличие от предыдущего метода, определение центральности направлено на выявление не самой главной вершины, а локальных «лидеров», которых может быть и пять, и десять. Таким образом Data Scientist может изучать распространение информации в сообществе (определять изначальное сообщение и следить за его распространением через несколько точек входа), отслеживать развитие болезней (строить карту заражений с нулевыми пациентами), контролировать телекоммуникационные и прочие сети.

Существует множество метрик центральности. В нашем примере мы расскажем, как найти на графе вершины, которые чаще всего связывают между собой разрозненные группы точек. На практике это может быть перевалочный пункт на географическом маршруте, «бутылочное горлышко» в каких-либо процессах, человек-посредник, который знакомит между собой других людей. В теории графов это и называется степенью посредничества (Betweenness Centrality).

Чтобы найти такие вершины, используйте следующий код:

pos = nx.spring_layout(subgraph_3437)
betweennessCentrality = nx.betweenness_centrality(subgraph_3437,normalized=True,
endpoints=True)
node_size = [v * 10000 for v in betweennessCentrality.values()]
plt.figure(figsize=(20,20))
nx.draw_networkx(subgraph_3437, pos=pos, with_labels=False,
node_size=node_size )
plt.axis(‘off’)

Чем больше диаметр круга, тем больше его степень посредничества. Если устранить эти узлы из системы, большой граф разобьется на несколько малых.

Мы рассмотрели всего пять графов, но даже такой краткий экскурс дает представление о том, какой это мощный инструмент Data Science. Изучайте графы, используйте их в своих проектах, и вы получите множество инсайтов о том, как работает наш постоянно меняющийся мир.

Источник

ИСПОЛЬЗОВАНИЕ ТЕОРИИ ГРАФОВ В РАЗРАБОТКЕ ПРОГРАММНЫХ СИСТЕМ

Введение

На сегодняшний день графы широко используются для представления данных и знаний в различных областях, таких как: электротехника, строительство и логистика, компьютерные и социальные сети, лингвистика и многие другие.

Теоретико-графовые конструкции (сети Петри, синтаксические деревья, модель программы в виде управляющего графа и др.) имеют существенное значение в развитие программирования и средств его автоматизации. Многие задачи анализа программ, возникающие при оптимизации, трансляции, проверке правильности, тестировании и т.д. значительно упрощаются, если рассматривать их на теоретико-графовых моделях.

Использование планарных графов

Планарные графы широко используются для решения задач, связанных с представлением планов помещений, карт и т.п.

Одним из примеров использования планарных графов является моделирование среды, в которой будет развиваться робот. Например, возьмём знаменитый «умный» пылесос. Робот должен учитывать «представление о мире», которое включает такую информацию как номера комнат и их топологии, возможность перейти непосредственно из одной комнаты в соседнюю, использование дверей и обходы запрещенных номеров. В этом случае, секторы в плоском графе представляют номера, а вершины – углы; если два номера соединены дверью, они имеют общее ребро в графе; а «запрещённые» номера помечены как невидимые (рис. 1), [].

Если робот достаточно «умён», он, возможно, построит эту модель самостоятельно. Именно эта модель будет «руководить» его работой: в соответствии с ней будет строиться план уборки помещений.

Рис. 1. Моделирование среды для робота: а) план помещения изображён (запрещённые комнаты отмечены специальным символом); б) планарный граф, представляющий помещение (серое пространство – видимые комнаты, белое – невидимые)

Ориентированные графы

Орграфы широко применяются в программировании как способ описания систем со сложными связями. Например, одна из основных структур, используемых при разработке компиляторов, для представления компьютерных программ, – граф потоков данных.

Рис. 2. Пример ориентированного графа

Поскольку информация, которую желательно визуализировать, постоянно усложняется, увеличивается её объём, возникает всё больше ситуаций, в которых требуются более мощные графовые формализмы для представления информационных моделей, имеющих, в частности, иерархическую структуру. Для их представления используются, например, хиграфы (hi-графы) и составные графы. Хиграфы являются обобщением понятия гиперграфа и представляют сложные отношения, используя многоуровневые “блобы”, которые могут содержать друг друга и пересекаться между собой. Составные графы являются расширением класса ориентированных графов за счет введения между вершинами дополнительного отношения включения и представляют собой менее общий формализм, чем хиграфы. Одним из современных неклассических формализмов являются кластерные графы. Кластерный граф состоит из неориентированного графа и рекурсивного разбиения его вершин на подмножества, называемые кластерами. Это относительно общий графовый формализм, который может использоваться во многих приложениях и хорошо приспособлен, в частности, для решения задач визуализации, рисования графов [].

Метаграфы

Впервые понятие вложенного метаграфа было использовано при описании состояний нечеткой ситуационной сети [], посредством которой моделировались неопределенные бизнес-процессы (рис. 3).

Ещё одним приложением вложенных метаграфов является организация семантического поиска в глобальных и корпоративных сетях или электронных библиотеках. В частности, сегодня при наличии огромного количества неструктурированных документов, наблюдается тенденция к формированию семантического Web. Метаграфы представляют мощный формализм, позволяющий решать задачи создания моделей документов и их систем, семантической разметки.

Метаграфы в настоящее время широко используются в решении задач планирования и управления организациями []. Представление бизнес-процесса как метаграфа – основа различных подходов к решению задач оптимизации ежедневной производственной деятельности организаций, в той или иной степени подверженных влиянию среды и неконтролируемых условий. В моделировании процессов с использованием метаграфов удобно применять принципы идемпотентной математики.

В работе [] был представлен разработанный авторами и реализованный программно алгоритм поиска метапути наименьшего веса в метаграфе, являющийся модификацией алгоритма Дейкстры с применением элементов идемпотентной математики.

Рис. 3. Фрагмент ситуационной сети бизнес-процесса

Ещё одна задача, решаемая с использованием метаграфов, – маршрутизация в IP-сетях с использованием [].

Иерархия архитектуры сетей может быть отражена с помощью метаграфов. В работе [] рассматривается протокол внутреннего шлюза OSPF (Open Shortest Path First, алгоритмы предложены Дейкстрой), который представляет собой протокол состояния маршрута (в качестве метрики для оценки используется коэффициент качества обслуживания).

Рис. 4. Пример метаграфа сети

Ещё одно приложение метаграфов – в реализации экономико-математических методов []. Метаграфы могут применяться и в таких традиционных для теории графов задачах, как транспортная задача и сетевое планирование.

В работе предлагается использовать метаграфы как оптимальный вариант формализации при решении задач создания языковых инструментариев, предназначенных для создания предметно-ориентированных языков [].

Гиперграфы

Одно из приложений – использование гиперграфов для представления онтологий. Пример представления онтологии сетевого оборудования с помощью гиперграфа показан на рис. 5, 6 [].

Рис. 5. Структура разработанной онтологии, описанная с помощью гиперграфа

В последние годы разработка онтологий переходит из мира лабораторий искусственного интеллекта на рабочие столы экспертов по предметным областям. Во всемирной паутине онтологии стали обычным явлением. Онтологии в сети варьируются от больших таксономий, категоризирующих web-сайты (как на сайте Yahoo!), до категоризации продаваемых товаров и их характеристик (как на сайте Amazon.com).

Для разных предметных областей и задач существует спектр языков представления знаний. Для системы, основанной на знаниях, одним из адекватных языков представления знаний является язык гиперграфов, используемых в качестве расширения семантических сетей.

Рис. 6. Образование новых семантических связей в структуре онтологии

В [] вводится понятие рёберного гиперграфа, в [] – м-ациклических и древовидных гиперграфов.

Если «умело» использовать гиперграфовые модели, то их можно применять в достаточно широких пределах.

Гиперграфы широко используются в лингвистической трансляции [], в качестве формальных моделей документов при решении задач информационного поиска и пр.

Аппарат гиперграфов позволяет описывать абзацы и даже полные тексты, не прибегая к использованию «гипертекстовых» технологий. Его можно применять для «метаописания» при определении понятий и отношений самой лингвистической модели и этапов трансляции. Гиперграфы позволяют встраивать специальные механизмы, например, ассоциированных (присоединенных) процедур. Более того, любые синтаксические или семантические отношения проверяются с помощью этих процедур.

Гиперграфовое представление имеет аналогии с семантическими сетями и с фреймами, но фреймы, сложно формализуются, а семантические сети до сих пор не имеют стандартного определения, хотя и возникли из формального понятия сети, которое по определению связано с гиперграфом. Гиперграф же имеет четкое формальное определение и теоретически обоснованную процедуру сопоставления (поиска изоморфизма). Сопоставление при решении задачи установления изоморфизма даёт спектр результатов в зависимости от структуры гиперграфов, степеней вершин и рёбер, их окраски и порядка выбора вершин с одинаковой степенью связности в графе. Таким образом, процедура поиска даёт возможность варьировать параметры при сопоставлении и получать разные результаты исходя из заданных внешних критериев.

Заключение

В настоящее время области научных исследований, связанных с разработкой программного обеспечения, где используются методы теории графов, значительно расширились по сравнению с традиционными приложениями теории графов. Одной из наиболее интересных задач, решение которых актуально для многих областей, традиционно является задача установления изоморфизма графов. Её решение может иметь особенности в зависимости от типа используемых графов и конкретных условий. Цель дальнейших исследований – изучение алгоритмов установления изоморфизма и разработка алгоритмов поиска подграфов, изоморфных заданному графу, в приложении к задачам реализации графовых грамматик.

Библиографический список

Астанин С.В., Драгныш Н.В., Жуковская Н.К. Вложенные метаграфы как модели сложных объектов.

Быкова В.В. М-ациклические и древовидные гиперграфы.

Касьянов В.Н. Применение графов в программировании.

Левин А.Г., Тышкевич Р.И. Дискретная математика, т. 5.

Погребной В.К. Алгоритм решения задачи определения изоморфизма гиперграфов. Томск.

Починский И.А. Использование гиперграфов для представления онтологии сетевого оборудования. Пенза.

Починский И.А. Формальное представление семантических гиперграфов и операций над ними. Пенза.

Сухов А.О. Анализ формализмов описания визуальных языков моделирования // Современные проблемы науки и образования. – 2012. – № 2; URL: www.science-education.ru/102-5655 (дата обращения: 01.03.2014).

Хахалин Г.К. Использование гиперграфов в лингвистической трансляции, 1999.

Черных О.О. Метаграфы в прикладной математики и области их применения. Липецк.

de la Higuera C. Polynomial algorithms for open plane graph and subgraph isomorphisms, 2013.

Источник