двоичный код 1001 соответствует десятичному числу
Перевести число 1010-1001 из двоичной системы в двоичную
Задача: перевести число 1010-1001 из двоичной в двоичную систему счисления.
Для перевода 1010-1001 из двоичной в двоичную систему счисления, воспользуемся следующим алгоритмом:
1. Для перевода числа 1010-1001 в десятичную систему воспользуемся формулой:
1010-10012=1 ∙ 2 8 + 0 ∙ 2 7 + 1 ∙ 2 6 + 0 ∙ 2 5 + — ∙ 2 4 + 1 ∙ 2 3 + 0 ∙ 2 2 + 0 ∙ 2 1 + 1 ∙ 2 0 = 1 ∙ 256 + 0 ∙ 128 + 1 ∙ 64 + 0 ∙ 32 + — ∙ 16 + 1 ∙ 8 + 0 ∙ 4 + 0 ∙ 2 + 1 ∙ 1 = 256 + 0 + 64 + 0 + 0 + 8 + 0 + 0 + 1 = 32910
2. Полученное число 329 переведем из десятичной системы счисления в двоичную. Для этого, осуществим последовательное деление на 2, до тех пор пока остаток не будет меньше чем 2.
| — | 329 | 2 | ||
| 328 | — | 164 | 2 | |
| 1 | 164 | — | 82 | 2 |
| 0 | 82 | — | 41 | 2 |
| 0 | 40 | — | 20 | 2 |
| 1 | 20 | — | 10 | 2 |
| 0 | 10 | — | 5 | 2 |
| 0 | 4 | — | 2 | 2 |
| 1 | 2 | 1 | ||
| 0 |
Полученные остатки записываем в обратном порядке, таким образом:
Перевести число 1101001101010.1001 из двоичной системы в восьмеричную
Задача: перевести число 1101001101010.1001 из двоичной в восьмеричную систему счисления.
Для перевода 1101001101010.1001 из двоичной в восьмеричную систему счисления, воспользуемся следующим алгоритмом:
1. Для перевода числа 1101001101010.1001 в десятичную систему воспользуемся формулой:
2. Полученное число 6762.5625 переведем из десятичной системы счисления в восьмеричную. Т.к. полученное число содержит дробную часть, нам потребуется перевести вначале целую часть, а затем дробную. Таким образом необходимо:
2.1 Для того, чтобы перевести число 6762 из десятичной системы счисления в восьмеричную, необходимо осуществить последовательное деление на 8, до тех пор пока остаток не будет меньше чем 8.
| — | 6762 | 8 | ||
| 6760 | — | 845 | 8 | |
| 2 | 840 | — | 105 | 8 |
| 5 | 104 | — | 13 | 8 |
| 1 | 8 | 1 | ||
| 5 |
Полученные остатки записываем в обратном порядке, таким образом:
2.2 Для перевода десятичной дроби 0.5625 в восьмеричную систему, необходимо выполнить последовательное умножение дроби на 8, до тех пор, пока дробная часть не станет равной 0 или пока не будет достигнута заданная точность вычисления. Получаем:
0.5625 ∙ 8 = 4.5 (4)
0.5 ∙ 8 = 4 (4)
Ответом станет прямая последовательность целых частей произведения. Т.е.
2.3. Осталось соединить переведенные части, таким образом:
Ответ: 1101001101010.10012 = 15152.448.
ДВОИЧНО-ДЕСЯТИЧНАЯ СИСТЕМА
Двоично-десятичная система счисления. Десятичные цифры от 0 до 9 заменяются представляющими их двоичными тетрадами: 0=0000, 1=0001, 2=0010, 3=0011, 4=0100, 5=0101, 6=0110, 7=0111, 8=1000 и 9=1001. Такая запись очень часто используется как промежуточный этап перевода числа из десятичной системы в двоичную или обратно. Так как 10 не является точной степенью 2, то используются не все 16 тетрад, а алгоритмы арифметических операций над многозначными числами здесь более сложны, чем в основных системах счисления. И тем не менее, двоично-десятичная система счисления применяется даже на этом уровне во многих микрокалькуляторах и некоторых компьютерах (в частности, «Ямаха» стандарта MSX).
Принцип построения этой системы достаточно прост: каждая десятичная цифра преобразуется прямо в свой десятичный эквивалент из 4 бит, например: 369110=0011 0110 1001 0001DEC:
Десятичное число 3 6 9 1 Двоично-десятичное число 0011 0110 1001 0001
Преобразуем двоично-десятичное число 1000 0000 0111 0010 в его десятичный эквивалент. Каждая группа из 4 бит преобразуется в её десятичный эквивалент. Получим 1000 0000 0111 0010DEC = 807210:
Двоично-десятичное число 1000 0000 0111 0010 Десятичное число 8 0 7 2
Микропроцессоры используют чистые двоичные числа, однако понимают и команды преобразования в двоично-десятичную запись. Полученные двоично-десятичные числа легко представимы в десятичной записи, более понятной людям.
Преобразование двоичных чисел в двоично-десятичные
Арифметико-логическое устройство AVR-микроконтроллеров (как и других микропроцессоров) выполняет элементарные арифметические и логические операции над числами, представленными в двоичном коде. В двоичном коде считываются результаты преобразования АЦП, в двоичном коде (в формате целых чисел или чисел с плавающей точкой) удобно выполнять обработку результатов измерения. Однако, когда окончательный результат отображается на индикаторе, он должен быть преобразован в десятичный формат, удобный для восприятия человеком.
В данном разделе рассматриваются программы преобразования двоичных чисел в двоично-десятичные.
1. Форматы представления десятичных чисел
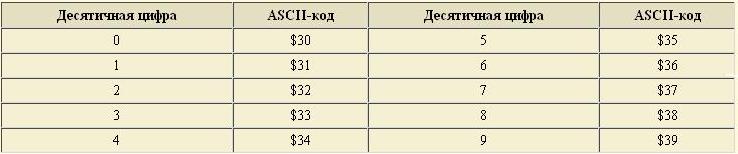
Неупакованный десятичный код является подмножеством международной таблицы кодирования символов ASCII (Таблица 1). Видно, что для хранения неупакованных десятичных чисел требуется в два раза больше памяти, так как каждая цифра представляется 8-битным кодом. Таблица 1: ASCII-коды десятичных цифр
2. Преобразование целых 16-битных чисел в двоично-десятичные числа
На сайте www.atmel.com предлагается программа «bin2bcd16» для преобразования целых 16-битных двоичных чисел в двоично-десятичные упакованные числа. В данной статье рассматривается программа «bin16bcd5» (см. Приложение, Программа 1), написанная Терешкиным А. В. согласно алгоритму, изложенному в [1], и выполняющая ту же задачу. Последняя программа по быстродействию, длине кода и количеству используемых регистров оказалась более эффективной, чем первая.
Алгоритм программы «bin16bcd5» заключается в следующем. Предположим, что имеется целое беззнаковое 16-битное число (диапазон от 0 до 65535). Очевидно, что необходимо найти 5 десятичных цифр. Способ преобразования заключается в том, чтобы, вычитая из исходного числа число 10000, сначала определить десятичную цифру десятков тысяч. Затем находится цифра тысяч последовательным вычитанием числа 1000 и т. д. Вычитание каждый раз производится до получения отрицательной разности с подсчетом числа вычитаний. При переходе к определению каждого следующего десятичного разряда в регистрах исходного числа восстанавливается последняя положительная разность. После того, как будет найдена десятичная цифра десятков, в регистрах исходного числа останется десятичная цифра единиц.
Программа «bin16ASCII5» (см. Приложение, Программа 2) преобразует целое двоичное 16-битное число в десятичное неупакованное число. При этом используется тот же алгоритм.
3. Преобразование двоичной дроби в двоично-десятичную дробь
Двоичная дробь, по определению, представляется следующим выражением:
Из этого представления следует алгоритм преобразования (Рис. 2), который содержит m шагов. На каждом шаге к двоично-десятичному результату прибавляется очередная двоичная цифра и весь результат делится на 2.
На изображены двоичный регистр, который содержит исходную двоичную дробь и регистр двоично-десятичного упакованного результата. Для наглядности у обоих регистров также показаны разряд единиц и положение точки, которые в памяти микропроцессора никак не представлены, но положение которых всегда строго оговорено. Количество циклов рассматриваемого алгоритма равно количеству бит двоичной дроби. Разрядность двоично-десятичного регистра определяется требуемой точностью вычислений.
Сложить эту цифру с двоично-десятичным числом означает, что ее нужно поместить в разряд единиц двоично-десятичного числа, откуда при последующем делении на два цифра A-i сдвинется в старший разряд старшей тетрады десятичной дроби. При программировании мы можем представлять, что разрядом единиц десятичной дроби является бит переноса С.
При делении на два двоично-десятичного упакованного числа, так же как и при делении двоичного числа, его сдвигают вправо на один разряд. При этом на два делится каждая тетрада, то есть каждая десятичная цифра. При делении четной десятичной цифры в соответствующем разряде снова получается десятичная цифра, и никакой коррекции не требуется. При делении на 2 нечетной десятичной цифры остаток, равный 5, должен быть добавлен к более младшему десятичному разряду, но на самом деле при двоичном сдвиге в более младшую тетраду добавляется число 8 (вес старшего разряда тетрады). Поэтому требуется коррекция результата, которая заключается в вычитании числа 3 из содержимого тех тетрад, которые после сдвига вправо имеют установленные старшие разряды.
4. Преобразование чисел с плавающей точкой в двоично-десятичные числа
Представление чисел с плавающей точкой имеет следующий вид:
Такое представление часто используется и в десятичной системе счисления для представления очень больших или очень малых чисел. Мантисса и порядок представляют собой целые знаковые числа. Знак мантиссы является знаком всего числа. Порядок показывает истинное положение точки вместо того, которое она занимает в изображении мантиссы. Двоичное число с плавающей точкой отличается от привычного нам десятичного тем, что точка является двоичной, то есть порядок показывает на количество двоичных (а не десятичных) разрядов, на которое необходимо переместить эту точку влево или вправо.
Нормализованным представлением числа с плавающей точкой называют такое представление, когда мантисса является правильной дробью, и старшая ее цифра отличается от нуля. Но для двоичного числа требование того, что старшая цифра отличается от нуля означает, что эта цифра равна 1. Если старшая цифра точно известна, то ее можно не хранить в памяти.
Перевести число 1001 из десятичной системы в десятичную
Задача: перевести число 1001 из десятичной системы счисления в 10-ую.
Для того, чтобы перевести число 1001 из десятичной системы счисления в 10-ую, необходимо осуществить последовательное деление на 10, до тех пор пока остаток не будет меньше чем 10.
| — | 1001 | 10 | ||
| 1000 | — | 100 | 10 | |
| 1 | 100 | — | 10 | 10 |
| 0 | 10 | 1 | ||
| 0 |
Полученные остатки записываем в обратном порядке, таким образом:
Задача: перевести число 1001 из 10-ой в 10-ую систему счисления.
Для перевода числа 1001 в десятичную систему воспользуемся формулой:
100110=1 ∙ 10 3 + 0 ∙ 10 2 + 0 ∙ 10 1 + 1 ∙ 10 0 = 1 ∙ 1000 + 0 ∙ 100 + 0 ∙ 10 + 1 ∙ 1 = 1000 + 0 + 0 + 1 = 100110
Подробнее о том, как переводить числа из десятичной системы в десятичную, смотрите здесь.
Подробнее о том, как переводить числа из десятичной системы в десятичную, смотрите здесь.