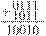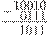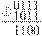двоичный код 4 разряда
Двоичное кодирование



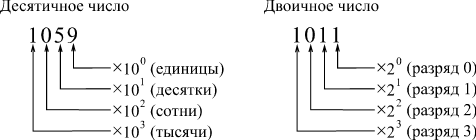
В отличие от привычного для нас десятичного кодирования чисел, то есть кода с основанием десять, при двоичном кодировании в основании кода лежит число два (рис. 2.9). То есть каждая цифра кода (каждый разряд) двоичного кода может принимать не десять значений (как в десятичном коде: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9), а всего лишь два — 0 и 1. Система позиционной записи остается такой же, то есть справа пишется самый младший разряд, а слева — самый старший. Но если в десятичной системе вес каждого следующего разряда больше веса предыдущего в десять раз, то в двоичной системе (при двоичном кодировании) — в два раза. Каждый разряд двоичного кода называется бит (от английского «Binary Digit» — «двоичное число»).
Рис. 2.9.Десятичное и двоичное кодирование
В табл. 2.3 показано соответствие первых двадцати чисел в десятичной и двоичной системах.
Из таблицы видно, что требуемое количество разрядов двоичного кода значительно больше, чем требуемое количество разрядов десятичного кода. Максимально возможное число при количестве разрядов, равном трем, составляет при десятичной системе 999, а при двоичной — всего лишь 7 (то есть 111 в двоичном коде). В общем случае n-разрядное двоичное число может принимать 2 n различных значений, а n-разрядное десятичное число — 10 n значений. То есть запись больших двоичных чисел (с количеством разрядов больше десяти) становится не слишком удобной.
| Таблица 2.3. Соответствие чисел в десятичной и двоичной системах | |||
| Десятичная система | Двоичная система | Десятичная система | Двоичная система |
Для того чтобы упростить запись двоичных чисел, была предложена так называемая шестнадцатиричная система (16-ричное кодирование). В этом случае все двоичные разряды разбиваются на группы по четыре разряда (начиная с младшего), а затем уже каждая группа кодируется одним символом. Каждая такая группа называется полубайтом (или нибблом, тетрадой ), а две группы (8 разрядов) — байтом. Из табл. 2.3 видно, что 4-разрядное двоичное число может принимать 16 разных значений (от 0 до 15). Поэтому требуемое число символов для шестнадцатиричного кода тоже равно 16, откуда и происходит название кода. В качестве первых 10 символов берутся цифры от 0 до 9, а затем используются 6 начальных заглавных букв латинского алфавита: A, B, C, D, E, F.
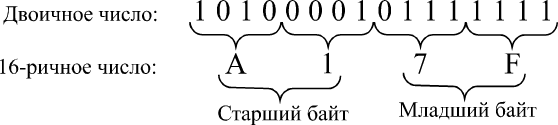
Рис. 2.10.Двоичная и 16-ричная запись числа
В табл. 2.4 приведены примеры 16-ричного кодирования первых 20 чисел (в скобках приведены двоичные числа), а на рис. 2.10 показан пример записи двоичного числа в 16-ричном виде. Для обозначения 16-ричного кодирования иногда применяют букву «h» или «H» (от английского Hexadecimal) в конце числа, например, запись A17F h обозначает 16-ричное число A17F. Здесь А1 представляет собой старший байт числа, а 7F — младший байт числа. Все число (в нашем случае — двухбайтовое) называется словом.
| Таблица 2.4. 16-ричная система кодирования | |||
| Десятичная система | 16-ричная система | Десятичная система | 16-ричная система |
| 0 (0000) | A (1010) | ||
| 1(0001) | B (1011) | ||
| 2 (0010) | C (1100) | ||
| 3 (0011) | D (1101) | ||
| 4 (0100) | E (1110) | ||
| 5 (0101) | F (1111) | ||
| 6 (0110) | 10 (00010000) | ||
| 7 (0111) | 11 (00010001) | ||
| 8 (1000) | 12 (00010010) | ||
| 9 (1001) | 13 (00010011) |
Для перевода 16-ричного числа в десятичное необходимо умножить значение младшего (нулевого) разряда на единицу, значение следующего (первого) разряда на 16, второго разряда на 256 (16 2 ) и т.д., а затем сложить все произведения. Например, возьмем число A17F:

A17F=F*16 0 + 7*16 1 + 1*16 2 + A*16 3 = 15*1 + 7*16+1*256+10*4096=41343
| Таблица 2.5. 8-ричная система кодирования | |||
| Десятичная система | 8-ричная система | Десятичная система | 8-ричная система |
| 0 (000) | 12 (001010) | ||
| 1(001) | 13 (001011) | ||
| 2 (010) | 14 (001100) | ||
| 3 (011) | 15 (001101) | ||
| 4 (100) | 16 (001110) | ||
| 5 (101) | 17 (001111) | ||
| 6 (110) | 20 (010000) | ||
| 7 (111) | 21 (010001) | ||
| 10 (001000) | 22 (010010) | ||
| 11 (001001) | 23 (010011) |
Но каждому специалисту по цифровой аппаратуре (разработчику, оператору, ремонтнику, программисту и т.д.) необходимо научиться так же свободно обращаться с 16-ричной и двоичной системами, как и с обычной десятичной, чтобы никаких переводов из системы в систему не требовалось.
Значительно реже, чем 16-ричное, используется восьмеричное кодирование, которое строится по такому же принципу, что и 16-ричное, но двоичные разряды разбиваются на группы по три разряда. Каждая группа (разряд кода) затем обозначается одним символом. Каждый разряд 8-ричного кода может принимать восемь значений: 0, 1, 2, 3, 4, 5, 6, 7 (табл. 2.5).
Помимо рассмотренных кодов, существует также и так называемое двоично-десятичное представление чисел. Как и в 16-ричном коде, в двоично-десятичном коде каждому разряду кода соответствует четыре двоичных разряда, однако каждая группа из четырех двоичных разрядов может принимать не шестнадцать, а только десять значений, кодируемых символами 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. То есть одному десятичному разряду соответствует четыре двоичных. В результате получается, что написание чисел в двоично-десятичном коде ничем не отличается от написания в обычном десятичном коде (табл. 2.6), но в реальности это всего лишь специальный двоичный код, каждый разряд которого может принимать только два значения: 0 и 1. Двоично-десятичный код иногда очень удобен для организации десятичных цифровых индикаторов и табло.
| Таблица 2.6. Двоично-десятичная система кодирования | |||
| Десятичная система | Двоично-десятичная система | Десятичная система | Двоично-десятичная система |
| 0 (0000) | 10 (00010000) | ||
| 1(0001) | 11 (00010001) | ||
| 2 (0010) | 12 (00010010) | ||
| 3 (0011) | 13 (00010011) | ||
| 4 (0100) | 14 (00010100) | ||
| 5 (0101) | 15 (00010101) | ||
| 6 (0110) | 16 (00010110) | ||
| 7 (0111) | 17 (00010111) | ||
| 8 (1000) | 18 (00011000) | ||
| 9 (1001) | 19 (00011001) |
В двоичном коде над числами можно проделывать любые арифметические операции: сложение, вычитание, умножение, деление.
Рассмотрим, например, сложение двух 4-разрядных двоичных чисел. Пусть надо сложить число 0111 (десятичное 7) и 1011 (десятичное 11). Сложение этих чисел не сложнее, чем в десятичном представлении:
Точно так же производится вычитание. Пусть из числа 10010 (18) надо вычесть число 0111 (7). Записываем числа с выравниванием по младшему разряду и вычитаем точно так же, как в случае десятичной системы:
При вычитании 0 из 0 получаем 0, при вычитании 0 из 1 получаем 1, при вычитании 1 из 1 получаем 0, при вычитании 1 из 0 получаем 1 и заем 1 в следующем разряде. Результат — 1011 (десятичное 11).
При вычитании возможно получение отрицательных чисел, поэтому необходимо использовать двоичное представление отрицательных чисел.
Для одновременного представления как двоичных положительных, так и двоичных отрицательных чисел чаще всего используется так называемый дополнительный код. Отрицательные числа в этом коде выражаются таким числом, которое, будучи сложено с положительным числом такой же величины, даст в результате нуль. Для того чтобы получить отрицательное число, надо поменять все биты такого же положительного числа на противоположные (0 на 1, 1 на 0) и прибавить к результату 1. Например, запишем число –5. Число 5 в двоичном коде выглядит 0101. Заменяем биты на противоположные: 1010 и прибавляем единицу: 1011. Суммируем результат с исходным числом: 1011 + 0101 = 0000 (перенос в пятый разряд игнорируем).
Помимо стандартных арифметических операций, в двоичной системе счисления используются и некоторые специфические операции, например, сложение по модулю 2. Эта операция (обозначается A) является побитовой, то есть никаких переносов из разряда в разряд и заемов в старших разрядах здесь не существует. Правила сложения по модулю 2 следующие: 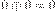
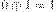
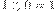
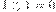
Среди других побитовых операций над двоичными числами можно отметить функцию И и функцию ИЛИ. Функция И дает в результате единицу только тогда, когда в соответствующих битах двух исходных чисел обе единицы, в противном случае результат —0. Функция ИЛИ дает в результате единицу тогда, когда хотя бы один из соответствующих битов исходных чисел равен 1, в противном случае результат 0.
Прямой, дополнительный и обратный коды
Прямой, дополнительный и обратный код числа (создан по запросу).
Далее идет калькулятор, который переводит введенное положительное или отрицательное целое число в двоичный код, а также выводит обратный код этого числа и его дополнительный код. Под калькулятором, как водится, немного теории.
Обновление: Из комментариев становится ясно, что люди не вполне понимают, что делает этот калькулятор. Точнее, что делал — применял алгоритм вычисления дополнительного кода к любому числу. Люди хотят, чтобы он им просто показывал дополнительный код числа. Ну хорошо — теперь при вводе положительного числа калькулятор показывает представление числа в двоичной форме, ибо для него нет обратного и дополнительного кода, а при вводе отрицательного показывает дополнительный и обратный код.
Прямой, дополнительный и обратный код
Прямой код числа это представление беззнакового двоичного числа. Если речь идет о машинной арифметике, то как правило на представление числа отводится определенное ограниченное число разрядов. Диапазон чисел, который можно представить числом разрядов n равен
Обратный код числа, или дополнение до единицы (one’s complement) это инвертирование прямого кода (поэтому его еще называют инверсный код). То есть все нули заменяются на единицы, а единицы на нули.
Дополнительный код числа, или дополнение до двойки (two’s complement) это обратный код, к младшему значащему разряду которого прибавлена единица
А теперь «зачем, зачем это все?» ©
Для различия положительных и отрицательных чисел выделяют старший разряд числа, который называется знаковым (sign bit)
0 в этом разряде говорит нам о том, что это положительное число, а 1 — отрицательное.
С положительными числами все вроде бы понятно, для их представления можно использовать прямой код
0 — 0000
1 — 0001
7 — 0111
А как представить отрицательные числа?
И это оказалось очень удобно для машинных вычислений — при таком представлении отрицательного числа операции сложения и вычитания можно реализовать одной схемой сложения, при этом очень легко определять переполнение результата (когда для представления получившегося числа не хватает разрядности)
Пара примеров
7-3=4
0111 прямой код 7
1101 дополнительный код 3
0100 результат сложения 4
-1+7=6
1111 дополнительный код 1
0111 прямой код 7
0110 результат сложения 6
Что касается переполнения — оно определяется по двум последним переносам, включая перенос за старший разряд. При этом если переносы 11 или 00, то переполнения не было, а если 01 или 10, то было. При этом, если переполнения не было, то выход за разряды можно игнорировать.
Примеры где показаны переносы и пятый разряд
00111 прямой код 7
00001 прямой код 1
01110 переносы
01000 результат 8 — переполнение
Два последних переноса 01 — переполнение
-7+7=0
00111 прямой код 7
01001 дополнительный код 7
11110 переносы
10000 результат 16 — но пятый разряд можно игнорировать, реальный результат 0
Два последних переноса 11 з перенос в пятый разряд можно отбросить, оставшийся результат, ноль, арифметически корректен.
Опять же проверять на переполнение можно простейшей операцией XOR двух бит переносов.
Вот благодаря таким удобным свойствам дополнительный код это самый распространенный способ представления отрицательных чисел в машинной арифметике.
Двоичный код 4 разряда

▪ Все статьи А-Я
▪ Энциклопедия радиоэлектроники и электротехники
▪ Новости науки и техники
▪ Архив статей и поиск
▪ Ваши истории из жизни
▪ На досуге
▪ Случайные статьи
▪ Отзывы о сайте

▪ Схемы и сервис-мануалы
▪ Книги, журналы, сборники
▪ Справочники
▪ Параметры радиодеталей
▪ Прошивки
▪ Инструкции по эксплуатации
▪ Энциклопедия радиоэлектроники и электротехники

(500000 статей в Архиве)


▪ Ваши истории
▪ Викторина онлайн
▪ Загадки для взрослых и детей
▪ Знаете ли Вы, что.
▪ Зрительные иллюзии
▪ Веселые задачки
▪ Каталог Вивасан
▪ Палиндромы
▪ Сборка кубика Рубика
▪ Форумы
▪ Голосования
▪ Карта сайта
Дизайн и поддержка:
Александр Кузнецов
Техническое обеспечение:
Михаил Булах
Программирование:
Данил Мончукин
Маркетинг:
Татьяна Анастасьева
При использовании материалов сайта обязательна ссылка на https://www.diagram.com.ua

сделано в Украине
О двоичной системе и кодах
В цифровой технике передаваемую, принятую или преобразованную информацию выражают набором символов двоичной системы счисления- двоичным кодом.
Любое привычное нам десятичное число может быть представлено как совокупность единиц и нулей этой системы. Десятичное число 7, например, в двоичной системе пишут так: 0111. Здесь крайний левый символ- старший разряд, а крайний правый символ-младший разряд четырехразрядного двоичного кодового числа. Перевод этого двоичного числа в число десятичной системы счисления выполняют в таком порядке: 0111=0X2 3 +1X2 2 +1X2 1 +1Х2 0 =0+4+2+1 =7.
В основе преобразования двоичного числа в десятичное лежит число 2. Сам же код в этом случае называют двоичным натуральным или кодом 8-4-2-1.
Переводить десятичные числа в двоичные и обратно в пределах четырехразрядного кода вам поможет таблица 1.
| Десятичное число | Двоичное число |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
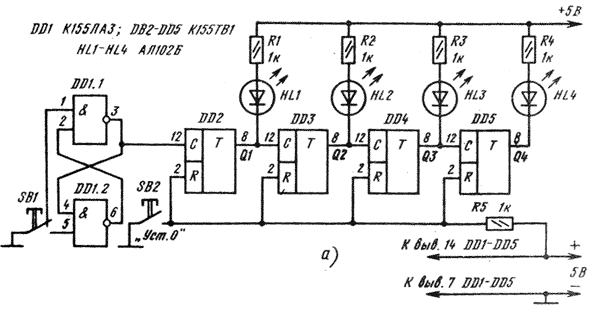
Чтобы прочнее закрепить в памяти принцип кодирования цифровой информации в двоичной системе, предлагаем опытным путем проанализировать работу четырехразрядного двоичного счетчика, собранного, например, на JK-триггерах по схеме, приведенной на рис. 1.
Рис. 1 Четырехразрядный счетчик
Все детали счетчика смонтируйте на макетной панели. К прямым выходам всех триггеров подключите светодиоды или иные индикаторы, по которым можно было бы визуально наблюдать за логическими состояниями триггеров. Функцию источника входных счетных импульсов большой длительности выполняет RS-триггер, собранный на логических элементах 2И-НЕ DD1.1, DD1.2 и управляемый кнопкой SB1.
Итак, проверьте монтаж, надежность паек и, если ошибок не обнаружите, включите питание. При этом некоторые светодиоды могут загореться, сигнализируя о том, что относящиеся к ним триггеры в момент включения питания оказались в единичном состоянии. Нажмите на кнопку SB2, чтобы. на вход R триггеров подать напряжение низкого уровня и тем самым установить все триггеры счетчика в нулевое состояние. Теперь все индикаторы погасли. Это логическое состояние всех триггеров четырехразрядного счетчика импульсов обозначьте в таблице нулями.
| Счет | Q1 | Q2 | Q3 | Q4 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 |
| 5 | 1 | 0 | 1 | 0 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 1 | 1 | 1 | 0 |
| 8 | 0 | 0 | 0 | 1 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 0 | 1 | 0 | 1 |
| 11 | 1 | 1 | 0 | 1 |
| 12 | 0 | 0 | 1 | 1 |
| 13 | 1 | 0 | 1 | 1 |
| 14 | 0 | 1 | 1 | 1 |
| 15 | 1 | 1 | 1 | 1 |
Теперь кратковременно нажмите и отпустите кнопку SB1. При этом RS-триггер переключится из нулевого состояния в единичное сам и напряжением высокого уровня на прямом выходе переключит в такое же состояние первый триггер счетчика. В результате включится светодиод HL1. Остальные триггеры счетчика будут сохранять нулевое состояние, и их светодиоды, естественно, светить не должны.
Третий входной импульс снова установит первый триггер счетчика в единичное состояние и не изменит состояние второго триггера, поэтому будут светить индикаторы HL1 и HL2. В таблице такое состояние счетчика запишите в таком виде: 1100. При четвертом входном импульсе будет светить только светодиод HL3, а в таблице должна появиться запись 0010.
Так, не торопясь, нажимая на кнопку SB1 и считывая по свечению индикаторов состояния триггеров, вы постепенно заполните всю таблицу логических состояний четырехразрядного счетчика. После этого отключите RS-триггер от входа счетчика и подайте на него от генератора последовательность импульсов, следующих с частотой 1. 2 Гц. Порядок вспахивания индикаторов, который при такой частоте можно проследить, подтвердит ваши записи, характеризующие работы двоичного четырехразрядного счетчика.
В результате получится: при первом входном импульсе-0001, при втором-0010, при третьем-0011 и т. д. до пятнадцатого импульса, когда кодовое состояние счетчика будет 1111, после чего счет импульсов повторяется. Короче говоря, эта таблица кода состояния счетчика, но, конечно, в перевернутом виде..
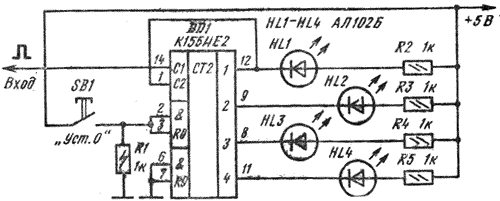
Подобные опыты с соответствующими выводами можно, разумеется, провести и с четырехразрядным счетчиком на D-триггерах, соединив их инверсные выходы с входами D, чтобы триггеры работали в счетном режиме. Полезно провести такое исследование и с микросхемой К155ИЕ2. Включив ее по схеме, изображенной на рис. 2, можно составить таблицу кодовых состояний такого счетчика импульсов от 0 до 9.
Рис. 2 Опыт с микросхемой К155ИЕ2