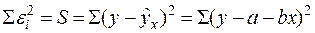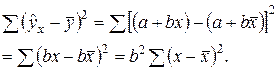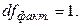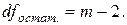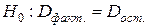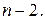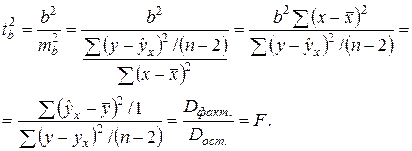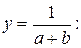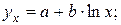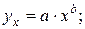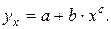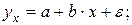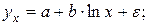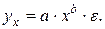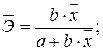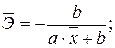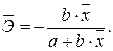эффективная оценка параметров классической линейной регрессионной модели оценка
Оценка результатов линейной регрессии
Введение
Модель линейной регрессии
Итак, у нас есть данные, состоящие из k наблюдений величин Y и Xi и мы хотим оценить коэффициенты. Стандартным методом для нахождения оценок коэффициентов является метод наименьших квадратов. И аналитическое решение, которое можно получить, применив этот метод, выглядит так: 
где b с крышкой — оценка вектора коэффициентов, y — вектор значений зависимой величины, а X — матрица размера k x n+1 (n — количество предикторов, k — количество наблюдений), у которой первый столбец состоит из единиц, второй — значения первого предиктора, третий — второго и так далее, а строки соответствуют имеющимся наблюдениям.
Функция summary.lm() и оценка получившихся результатов
Теперь рассмотрим пример построения модели линейной регрессии в языке R:
Таблица gala содержит некоторые данные о 30 Галапагосских островах. Мы будем рассматривать модель, где Species — количество разных видов растений на острове линейно зависит от нескольких других переменных.
Рассмотрим вывод функции summary.lm().
Сначала идет строка, которая напоминает, как строилась модель.
Затем идет информация о распределении остатков: минимум, первая квартиль, медиана, третья квартиль, максимум. В этом месте было бы полезно не только посмотреть на некоторые квантили остатков, но и проверить их на нормальность, например тестом Шапиро-Уилка.
Далее — самое интересное — информация о коэффициентах. Здесь потребуется немного теории.
Сначала выпишем следующий результат: 
при этом сигма в квадрате с крышкой является несмещенной оценкой для реальной сигмы в квадрате. Здесь b — реальный вектор коэффициентов, а эпсилон с крышкой — вектор остатков, если в качестве коэффициентов взять оценки, полученные методом наименьших квадратов. То есть при предположении, что ошибки распределены нормально, вектор коэффициентов тоже будет распределен нормально вокруг реального значения, а его дисперсию можно несмещенно оценить. Это значит, что можно проверять гипотезу на равенство коэффициентов нулю, а следовательно проверять значимость предикторов, то есть действительно ли величина Xi сильно влияет на качество построенной модели.
Для проверки этой гипотезы нам понадобится следующая статистика, имеющая распределение Стьюдента в том случае, если реальное значение коэффициента bi равно 0: 
где

Теперь все готово для продолжения разбора вывода функции summary.lm().
Итак, далее идут оценки коэффициентов, полученные методом наименьших квадратов, их стандартные ошибки, значения t-статистики и p-значения для нее. Обычно p-значение сравнивается с каким-нибудь достаточно малым заранее выбранным порогом, например 0.05 или 0.01. И если значение p-статистики оказывается меньше порога, то гипотеза отвергается, если же больше, ничего конкретного, к сожалению, сказать нельзя. Напомню, что в данном случае, так как распределение Стьюдента симметричное относительно 0, то p-значение будет равно 1-F(|t|)+F(-|t|), где F — функция распределения Стьюдента с k-n-1 степенями свободы. Также, R любезно обозначает звездочками значимые коэффициенты, для которых p-значение достаточно мало. То есть, те коэффициенты, которые с очень малой вероятностью равны 0. В строке Signif. codes как раз содержится расшифровка звездочек: если их три, то p-значение от 0 до 0.001, если две, то оно от 0.001 до 0.01 и так далее. Если никаких значков нет, то р-значение больше 0.1.
В нашем примере можно с большой уверенностью сказать, что предикторы Elevation и Adjacent действительно с большой вероятностью влияют на величину Species, а вот про остальные предикторы ничего определенного сказать нельзя. Обычно, в таких случаях предикторы убирают по одному и смотрят, насколько изменяются другие показатели модели, например BIC или Adjusted R-squared, который будет разобран далее.
Значение Residual standart error соответствует просто оценке сигмы с крышкой, а степени свободы вычисляются как k-n-1.
А теперь самая важные статистики, на которые в первую очередь стоит смотреть: R-squared и Adjusted R-squared: 
где Yi — реальные значения Y в каждом наблюдении, Yi с крышкой — значения, предсказанные моделью, Y с чертой — среднее по всем реальным значениям Yi.
Начнем со статистики R-квадрат или, как ее иногда называют, коэффициента детерминации. Она показывает, насколько условная дисперсия модели отличается от дисперсии реальных значений Y. Если этот коэффициент близок к 1, то условная дисперсия модели достаточно мала и весьма вероятно, что модель неплохо описывает данные. Если же коэффициент R-квадрат сильно меньше, например, меньше 0.5, то, с большой долей уверенности модель не отражает реальное положение вещей.
Однако, у статистики R-квадрат есть один серьезный недостаток: при увеличении числа предикторов эта статистика может только возрастать. Поэтому, может показаться, что модель с большим количеством предикторов лучше, чем модель с меньшим, даже если все новые предикторы никак не влияют на зависимую переменную. Тут можно вспомнить про принцип бритвы Оккама. Следуя ему, по возможности, стоит избавляться от лишних предикторов в модели, поскольку она становится более простой и понятной. Для этих целей была придумана статистика скорректированный R-квадрат. Она представляет собой обычный R-квадрат, но со штрафом за большое количество предикторов. Основная идея: если новые независимые переменные дают большой вклад в качество модели, значение этой статистики растет, если нет — то наоборот уменьшается.
Для примера рассмотрим ту же модель, что и раньше, но теперь вместо пяти предикторов оставим два:
Как можно увидеть, значение статистики R-квадрат снизилось, однако значение скорректированного R-квадрат даже немного возросло.
Теперь проверим гипотезу о равенстве нулю всех коэффициентов при предикторах. То есть, гипотезу о том, зависит ли вообще величина Y от величин Xi линейно. Для этого можно использовать следующую статистику, которая, если гипотеза о равенстве нулю всех коэффициентов верна, имеет распределение Фишера c n и k-n-1 степенями свободы: 
Значение F-статистики и p-значение для нее находятся в последней строке вывода функции summary.lm().
Заключение
В этой статье были описаны стандартные методы оценки значимости коэффициентов и некоторые критерии оценки качества построенной линейной модели. К сожалению, я не касался вопроса рассмотрения распределения остатков и проверки его на нормальность, поскольку это увеличило бы статью еще вдвое, хотя это и достаточно важный элемент проверки адекватности модели.
Очень надеюсь что мне удалось немного расширить стандартное представление о линейной регрессии, как об алгоритме который просто оценивает некоторый вид зависимости, и показать, как можно оценить его результаты.
Линейная регрессия
Линейная регрессия (Linear regression) — это это математическая модель, которая описывает связь нескольких переменных. Модели линейной регрессии представляют собой статистическую процедуру, помогающую прогнозировать будущее. Она применяется в научных сферах и в бизнесе, а в последние десятилетия используется в машинном обучении.
Для чего нужна линейная регрессия
Задача регрессии в машинном обучении — это предсказание одного параметра (Y) по известному параметру X, где X — набор параметров, характеризующий наблюдение.
Как работает линейная регрессия
Возьмем небольшой набор данных. Предположим, что это группа коттеджей, расположенных в одном районе. На оси Х обозначена их площадь, а на оси Y — рыночная стоимость. Чтобы увидеть, как стоимость дома зависит от его площади, построим регрессию.
Это будет простая линейная регрессия с одной переменной. Изменится площадь дома — изменится и стоимость. Для вычисления используем стандартное уравнение регрессии: f (x) = b + m⋅x, где m — это наклон линии, а b — ее сдвиг по оси Y. То есть изменение коэффициентов m и b будет влиять на расположение прямой:
Провести прямую линию через все точки на графике не получится, если они расположены в хаотичном порядке. Поэтому с помощью линейной регрессии определяется оптимальный вариант расположения этой прямой. Некоторые точки все равно останутся на расстоянии, но оно должно быть минимальным. Расчет этого минимального расстояния от прямой до каждой точки называется функцией потерь.
Для оценки точности регрессии используют разные метрики, например MSE (от англ. mean squared error — средняя квадратическая ошибка). Чем ниже MSE, тем лучше модель.
В первом случае MSE будет равна 0,17, во втором — 0,08, а в третьем — 0,02. Получается, что третья прямая лучше всего показывает зависимость цены дома от его площади.
Data Scientist с нуля
Получите востребованные IT-навыки за один год и станьте перспективным профессионалом. Мы поможем в трудоустройстве. Дополнительная скидка 5% по промокоду BLOG.
Расчет линейной регрессии в Python
Построим регрессию, чтобы узнать, как кассовые сборы фильма зависят от бюджета, который вложили в его производство.
Для расчета понадобится csv-файл, который содержит информацию о бюджетах и сборах 5 034 фильмов, которые когда-то выходили в прокат. Эти данные станут базой для исследования.
Построим модель линейной регрессии с помощью Python. Для этого нужно импортировать несколько библиотек:
Модель линейной регрессии, которую нужно будет обучить, импортируется с помощью библиотеки sklearn. В качестве X будет колонка production_budget_usd, а в качестве Y – колонка worldwide_gross_usd.
На основе этих данных определяется нужный наклон прямой и расположение относительно осей координат. Это и будет нужной линейной регрессией, по которой можно предсказать сборы собственного фильма, выбрав подходящий бюджет.
В итоге получится график того, как соотносятся бюджеты и кассы у фильмов в списке. Каждая точка — это отдельная кинолента. На оси Х показаны затраты на производство, а на оси У — сколько она заработала. Теперь через эти точки нужно провести прямую так, чтобы она была максимально близка ко всем точкам на графике.
Множественная линейная регрессия
В жизни кассовые сборы кино зависят не от одной переменной, а от совокупности разных факторов: популярности жанра, режиссера, каста актеров и затрат на промокампанию. Если рассчитать все факторы, влияющие на сборы, то уравнение изменится:
Стало f(x) = b + m1*x1 + … + mn*xn
Каждый коэффициент в нем показывает важность признаков. То есть множественная регрессия демонстрирует, как каждый параметр влияет на расположение прямой, и выбирает оптимальный вариант точно так же, как и линейная — с помощью функции потерь.
Data Scientist с нуля
Получите востребованные IT-навыки за один год и станьте перспективным профессионалом. Мы поможем в трудоустройстве. Дополнительная скидка 5% по промокоду BLOG.
Оценка параметров линейного регрессионного уравнения
Для оценки параметров регрессионного уравнения наиболее часто используют метод наименьших квадратов (МНК), в основе которого лежит предположение о независимости наблюдений исследуемой совокупности. Сущность данного метода заключается в нахождении параметров модели (α, β), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:
В итоге получаем систему нормальных уравнений:
Эту систему можно записать в виде:
Решая данную систему линейных уравнений с двумя неизвестными получаем оценки наименьших квадратов:
В уравнениях регрессии параметр α показывает усредненное влияние на результативный признак неучтенных факторов, а параметр β – коэффициент регрессии показывает, насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу.
Между линейным коэффициентом корреляции и коэффициентом регрессии существует определенная зависимость, выражаемая формулой:
где – коэффициент регрессии в уравнении связи;
– среднее квадратическое отклонение соответствующего статистически существенного факторного признака.
Имеются следующие данные о размере страховой суммы и страховых возмещений на автотранспортные средства одной из страховых компаний.
Зависимость между размером страховых возмещений и страховой суммой на автотранспорт
Объем страхового возмещения (тыс.долл.), Yi
Стоимость застрахованного автомобиля (тыс.долл.), X i
Оценка параметров линейной регрессии
Линейная регрессия сводится к нахождению уравнения вида:
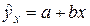 (или (или 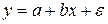 ). ). | (3) |
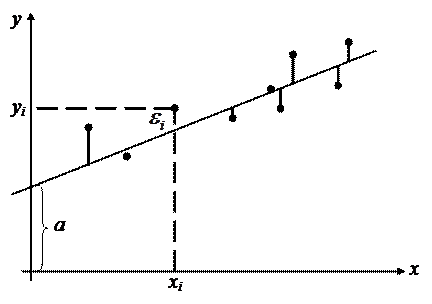 |
Рис. 2.1. График линии регрессии
Первое выражение позволяет по заданным значениям фактора x рассчитать теоретические значения результативного признака, подставляя в него фактические значения фактора x. На графике теоретические значения лежат на прямой, которые представляют собой линию регрессии (рис. 2.1).
Построение линейной регрессии сводится к оценке ее параметров а и b. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).
МНК позволяет получить такие оценки параметров а и b, при которых сумма квадратов отклонений фактических значений 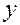

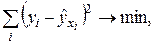 или или 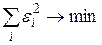 . . | (4) |
Для нахождения минимума надо вычислить частные производные суммы (4) по каждому из параметров – а и b – и приравнять их к нулю.
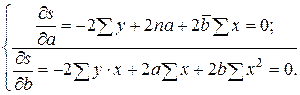
Преобразуем, получаем систему нормальных уравнений:
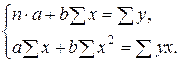

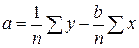
Выражение (7) можно записать в другом виде:
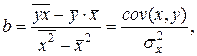
где 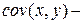
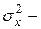
Параметр b называется коэффициентом регрессии.Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение парной регрессии достаточно распространенным в эконометрических исследованиях.
Формально a – значение y при x = 0. Если x не имеет и не может иметь нулевого значения, то такая трактовка свободного члена a не имеет смысла. Параметр a может не иметь экономического содержания. Попытки экономически интерпретировать его могут привести к абсурду, особенно при a 0, то относительное изменение результата происходит медленнее, чем изменение фактора. Сравним эти относительные изменения:
 . . | (12) |
Величина 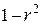
2.3. Предпосылки МНК (условия Гаусса-Маркова)
Связь между y и x в парной регрессии является не функциональной, а корреляционной. Поэтому оценки параметров a и b являются случайными величинами, свойства которых существенно зависят от свойств случайной составляющей ε. Для получения по МНК наилучших результатов необходимо выполнение следующих предпосылок относительно случайного отклонения (условия Гаусса-Маркова):
1. Математическое ожидание случайного отклонения равно нулю для всех наблюдений: 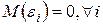
2. Дисперсия случайных отклонений постоянна: 
3. Случайные отклонения εi и εj являются независимыми друг от друга для 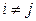
Выполнимость этого условия называется отсутствием автокорреляции.
4. Случайное отклонение должно быть независимо от объясняющих переменных. Обычно это условие выполняется автоматически, если объясняющие переменные в данной модели не являются случайными. Кроме того, выполнимость данной предпосылки для эконометрических моделей не столь критична по сравнению с первыми тремя.
При выполнимости указанных предпосылок имеет место теорема Гаусса-Маркова: оценки (7) и (8), полученные по МНК, имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.
Таким образом, при выполнении условий Гаусса—Маркова оценки (7) и (8) являются не только несмещенными оценками коэффициентов регрессии, но и наиболее эффективными, т. е. имеют наименьшую дисперсию по сравнению с любыми другими оценками данных параметров, линейными относительно величин yi.
Именно понимание важности условий Гаусса—Маркова отличает компетентного исследователя, использующего регрессионный анализ, от некомпетентного. Если эти условия не выполнены, исследователь должен это сознавать. Если корректирующие действия возможны, то аналитик должен быть в состоянии их выполнить. Если ситуацию исправить невозможно, исследователь должен быть способен оценить, насколько серьезно это может повлиять на результаты.
2.4. Оценка существенности параметров линейной
регрессии и корреляции
После того, как найдено уравнение линейной регрессии (3), проводится оценка значимости как уравнения в целом, так и отдельных его параметров.
Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза 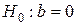
Перед расчетом критерия проводятся анализ дисперсии. Можно показать, что общая сумма квадратов отклонений (СКО) y от среднего значения 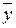
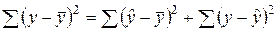
|
или, соответственно:
 |
 |
Здесь возможны два крайних случая: когда общая СКО в точности равна остаточной и когда общая СКО равна факторной.
В первом случае фактор х не оказывает влияния на результат, вся дисперсия y обусловлена воздействием прочих факторов, линия регрессии параллельна оси Ох и 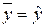
Во втором случае прочие факторы не влияют на результат, y связан с x функционально, и остаточная СКО равна нулю.
Но на практике в правой части (13) присутствуют оба слагаемых. Пригодность линии регрессии для прогноза зависит от того, какая часть общей вариации y приходится на объясненную вариацию. Если объясненная СКО будет больше остаточной СКО, то уравнение регрессии статистически значимо и фактор х оказывает существенное воздействие на результат y. Это равносильно тому, что коэффициент детерминации будет приближаться к единице.
Для общей СКО требуется 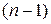
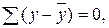
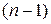

Факторную СКО можно выразить так:
Эта СКО зависит только от одного параметра b, поскольку выражение под знаком суммы к значениям результативного признака не относится. Следовательно, факторная СКО имеет одну степень свободы, и
Для определения 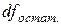
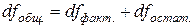
Таким образом, можем записать 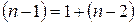
Разделив каждую СКО на свое число степеней свободы, получим средний квадрат отклонений,или дисперсию на одну степень свободы:
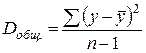
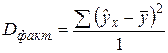
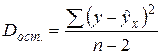
Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим F-критерий для проверки нулевой гипотезы, которая в данном случае записывается как
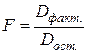
Если 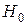
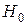
Английским статистиком Снедекором разработаны таблицы критических значений F при разных уровнях существенности Снедекором и различных числах степеней свободы. Табличное значение F-критерия – это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы.
При нахождении табличного значения F-критерия задается уровень значимости (обычно 0,05 или 0,01) и две степени свободы – числителя (она равна единице) и знаменателя, равная
Вычисленное значение F признается достоверным (отличным от единицы), если оно больше табличного, т. е. 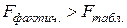
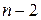
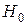
Если 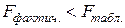
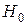
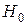
Величина F-критерия связана с коэффициентом детерминации.
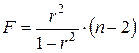
В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров.
Стандартная ошибка коэффициента регрессии определяется по формуле:
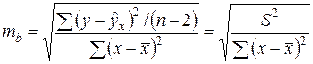
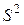
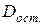
Величина стандартной ошибки совместно с t-распределением Стьюдента при 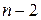
Величина коэффициента регрессии сравнивается с его стандартной ошибкой; определяется фактическое значение t-критерия Стьюдента
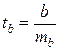
которое затем сравнивается с табличным значением при определенном уровне значимости α и числе степеней свободы 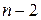
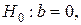
Если 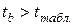
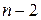
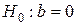
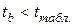
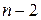
Существует связь между 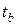
Отсюда следует, что
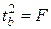
Доверительный интервал для b определяется как
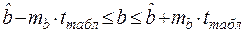
где 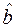
Стандартная ошибка параметра 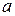
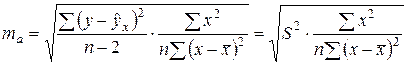
Процедура оценивания существенности a не отличается от таковой для параметра b. При этом фактическое значение t-критерия вычисляется по формуле:
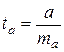
Процедура проверки значимости линейного коэффициента корреляции отличается от процедур, приведенных выше. Это объясняется тем, что r как случайная величина распределена по нормальному закону лишь при большом числе наблюдений и малых значениях |r|. В этом случае гипотеза об отсутствии корреляционной связи между y и х 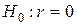
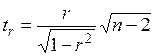
которая при справедливости 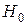
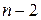
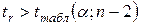
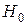
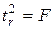
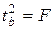
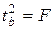
Но при малых выборках и значениях r, близких к 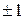
Чтобы обойти это затруднение, используется так называемое
z-преобразование Фишера:


Для величины z имеются таблицы, в которых приведены её значения для соответствующих значений r.
Для z выдвигается нуль-гипотеза 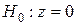
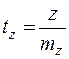
которая распределена по закону Стьюдента с ( 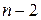
Для каждого значения z можно вычислить критические значения r. Таблицы критических значений r разработаны для уровней значимости 0,05 и 0,01 и соответствующего числа степеней свободы. Если вычисленное значение r превышает по абсолютной величине табличное, то данное значение r считается существенным. В противном случае фактическое значение несущественно.
2.5. Нелинейные модели регрессии
и их линеаризация
До сих пор мы рассматривали лишь линейную модель регрессионной зависимости y от x (3). В то же время многие важные связи в экономике являются нелинейными. Примерами такого рода регрессионных моделей являются производственные функции (зависимости между объемом произведенной продукции и основными факторами производства – трудом, капиталом и т. п.) и функции спроса (зависимости между спросом на какой-либо вид товаров или услуг, с одной стороны, и доходом и ценами на этот и другие товары – с другой).
При анализе нелинейных регрессионных зависимостей наиболее важным вопросом применения классического МНК является способ их линеаризации. В случае линеаризации нелинейной зависимости получаем линейное регрессионное уравнение типа (3), параметры которого оцениваются обычным МНК, после чего можно записать исходное нелинейное соотношение.
Несколько особняком в этом смысле стоит полиномиальная модель произвольной степени:
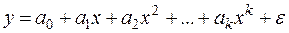
к которой обычный МНК можно применять без всякой предварительной линеаризации.
Рассмотрим указанную процедуру применительно к параболе второй степени:

Такая зависимость целесообразна в случае, если для некоторого интервала значений фактора возрастающая зависимость меняется на убывающую или наоборот. В этом случае можно определить значение фактора, при котором достигается максимальное или минимальное значение результативного признака. Если исходные данные не обнаруживают изменение направленности связи, параметры параболы становятся трудно интерпретируемыми, и форму связи лучше заменить другими нелинейными моделями.
Применение МНК для оценки параметров параболы второй степени сводится к дифференцированию суммы квадратов остатков регрессии по каждому из оцениваемых параметров и приравниванию полученных выражений нулю. Получается система нормальных уравнений, число которых равно числу оцениваемых параметров, т. е. трем:
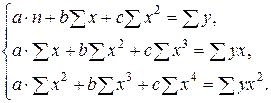
Решать эту систему можно любым способом, в частности, методом определителей.
Экстремальное значение функции наблюдается при значении фактора, равном:
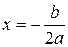
Если 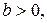
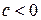
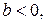
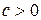
В нелинейных зависимостях, неявляющихся классическими полиномами, обязательно проводится предварительная линеаризация, которая заключается в преобразовании или переменных, или параметров модели, или в комбинации этих преобразований. Рассмотрим некоторые классы таких зависимостей.
Зависимости гиперболического типа имеют вид:
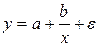
Примером такой зависимости является кривая Филлипса, констатирующая обратную зависимость процента прироста заработной платы от уровня безработицы. В этом случае значение параметра b будет больше нуля.
Другим примером зависимости (33) являются кривые Энгеля, формулирующие следующую закономерность: с ростом дохода доля доходов, расходуемых на продовольствие, уменьшается, а доля доходов, расходуемых на непродовольственные товары, будет возрастать. В этом случае 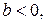
Линеаризация уравнения (33) сводится к замене фактора 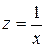
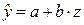
К такому же линейному уравнению сводится полулогарифмическая кривая:
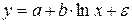
которая может быть использована для описания кривых Энгеля. Здесь ln(x) заменяется на z и получается уравнение (34).
Достаточно широкий класс экономических показателей характеризуется приблизительно постоянным темпом относительного прироста во времени. Этому соответствуют зависимости показательного (экспоненциального) типа, которые записываются в виде:
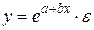
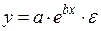
Возможна и такая зависимость:
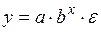
В регрессиях типа (36) – (38) применяется один и тот же способ линеаризации – логарифмирование. Уравнение (36) приводится к виду:
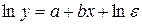
Замена переменной 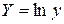
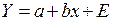
где 

который отличается от (39) только видом свободного члена, и линейное уравнение выглядит так:
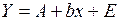
где 

где 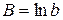
Широко распространены в практике социально-экономических исследований степенные зависимости. Они используются для построения и анализа производственных функций. В функциях вида:
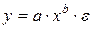
особенно ценным является то обстоятельство, что параметр b равен коэффициенту эластичности результативного признака по фактору х. Преобразуя (44) путем логарифмирования, получаем линейную регрессию:
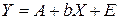
где 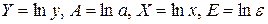
Еще одним видом нелинейности, приводимым к линейному виду, является обратная зависимость:
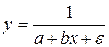
Проводя замену 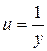
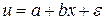
Наконец, следует отметить зависимость логистического типа:
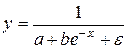
Графиком функции (48) является так называемая «кривая насыщения», которая имеет две горизонтальные асимптоты 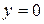

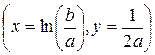
 |
Рис. 2.2. Кривая насыщения
Уравнение (48) приводится к линейному виду заменами переменных 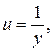
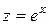
Любое уравнение нелинейной регрессии, как и линейной зависимости, дополняется показателем корреляции, который в данном случае называется индексом корреляции:
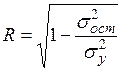
Здесь 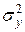
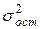
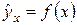
Следует обратить внимание на то, что разности в соответствующих суммах 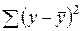
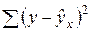
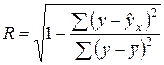
Величина R находится в границах 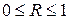
Так обстоит дело с полулогарифмической и полиномиальной регрессией, а также с равносторонней гиперболой (33). Определив линейный коэффициент корреляции для линеаризованных уравнений, например, в пакете Excel с помощью функции ЛИНЕЙН, можно использовать его и для нелинейной зависимости.
Иначе обстоит дело в случае, когда преобразование проводится также с величиной y, например, взятие обратной величины или логарифмирование. Тогда значение R, вычисленное той же функцией ЛИНЕЙН, будет относиться к линеаризованному уравнению регрессии, а не к исходному нелинейному уравнению, и величины разностей под суммами в (50) будут относиться к преобразованным величинам, а не к исходным, что не одно и то же. При этом, как было сказано выше, для расчета R следует воспользоваться выражением (50), вычисленным по исходному нелинейному уравнению.
Поскольку в расчете индекса корреляции используется соотношение факторной и общей СКО, то R 2 имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину R 2 для нелинейных связей называют индексом детерминации.
Оценка существенности индекса корреляции проводится так же, как и оценка надежности коэффициента корреляции.
Индекс детерминации используется для проверки существенности в целом уравнения нелинейной регрессии по F-критерию Фишера:
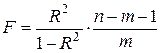
Во всех рассмотренных нами случаях, кроме полиномиальной регрессии, 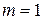
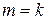
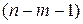
Близость этих показателей означает, что усложнять форму уравнения регрессии не следует и можно использовать линейную функцию. Практически, если величина 
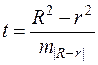
Здесь в знаменателе находится ошибка разности 
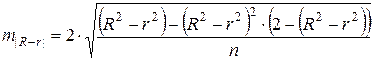
Если 
В заключение в таблице 2.2 приведем формулы расчета коэффициентов эластичности для наиболее распространенных уравнений регрессии.
| Вид уравнения регрессии | Коэффициент эластичности |
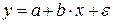 | 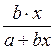 |
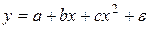 | 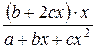 |
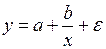 | 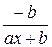 |
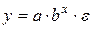 | 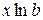 |
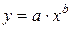 | 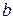 |
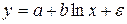 | 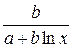 |
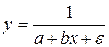 |  |
Контрольные вопросы
1. В чем состоит суть метода наименьших квадратов?
2. В каком случае остаточная сумма квадратов равна нулю?
3. Объясненная (факторная) сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное…
4. Остаточная сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное…
5. На чем основан классический метод к оцениванию параметров регрессии?
6. Какое уравнение регрессии нельзя свести к линейному виду:
a)
b)
c)
7. Какие значения может принимать коэффициент корреляции 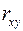
8. Какое из следующих уравнений нелинейно по оцениваемым параметрам:
a)
b)
c)
9. Для функции 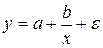
a)
b)
c)
3. ЛИНЕЙНАЯ МОДЕЛЬ МНОЖЕСТВЕННОЙ
РЕГРЕССИИ