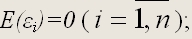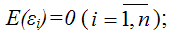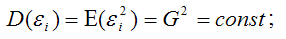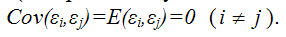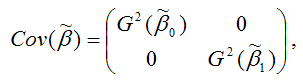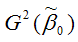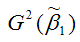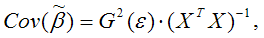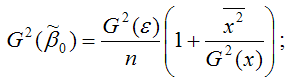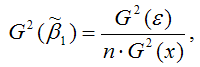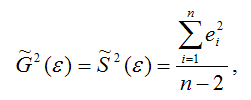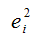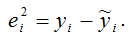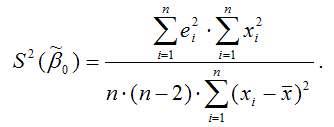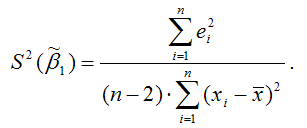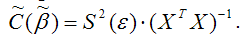эффективность оценки параметра регрессии полученной по мнк означает
Множественная регрессия и корреляция
Тестовые задания
Парная регрессия и корреляция
1. Наиболее наглядным видом выбора уравнения парной регрессии является:
2. Рассчитывать параметры парной линейной регрессии можно, если у нас есть:
б) не менее 7 наблюдений;
3. Суть метода наименьших квадратов состоит в:
б) минимизации дисперсии результативного признака;
4. Коэффициент линейного парного уравнения регрессии:
а) показывает среднее изменение результата с изменением фактора на одну единицу;
5. На основании наблюдений за 50 семьями построено уравнение регрессии 


6. Суть коэффициента детерминации 
б) характеризует долю дисперсии результативного признака 
7. Качество модели из относительных отклонений по каждому наблюдению оценивает:
а) коэффициент детерминации 
8. Значимость уравнения регрессии в целом оценивает:
а) 
9. Классический метод к оцениванию параметров регрессии основан на:
в) шаговом регрессионном анализе.
10. Остаточная сумма квадратов равна нулю:
11. Объясненная (факторная) сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:
б) 
12. Остаточная сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:
в) 
13. Общая сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:
а) 
14. Для оценки значимости коэффициентов регрессии рассчитывают:
в) коэффициент детерминации 
15. Какое уравнение регрессии нельзя свести к линейному виду:
в) 
16. Какое из уравнений является степенным:
б) 
17. Параметр 
б) коэффициентом эластичности;
18. Коэффициент корреляции 
19. Для функции 
б) 
20. Какое из следующих уравнений нелинейно по оцениваемым параметрам:
в) 
Множественная регрессия и корреляция
1. Добавление в уравнение множественной регрессии новой объясняющей переменной:
б) увеличивает значение коэффициента детерминации;
2. Скорректированный коэффициент детерминации:
в) меньше или равен обычному коэффициенту детерминации;
3. С увеличением числа объясняющих переменных скорректированный коэффициент детерминации:
4. Число степеней свободы для остаточной суммы квадратов в линейной модели множественной регрессии равно:
б) 
5. Число степеней свободы для общей суммы квадратов в линейной модели множественной регрессии равно:
а) 
6. Число степеней свободы для факторной суммы квадратов в линейной модели множественной регрессии равно:
в) 
7. Множественный коэффициент корреляции 



8. Для построения модели линейной множественной регрессии вида 
9. Стандартизованные коэффициенты регрессии 
а) позволяют ранжировать факторы по силе их влияния на результат;
10. Частные коэффициенты корреляции:
в) характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании других факторов, включенных в уравнение регрессии.
11. Частный 
б) служит мерой для оценки включения фактора в модель;
12. Несмещенность оценки параметра регрессии, полученной по МНК, означает:
б) что математическое ожидание остатков равно нулю;
13. Эффективность оценки параметра регрессии, полученной по МНК, означает:
а) что она характеризуется наименьшей дисперсией;
14. Состоятельность оценки параметра регрессии, полученной по МНК, означает:
в) увеличение ее точности с увеличением объема выборки.
15. Укажите истинное утверждение:
в) при наличии гетероскедастичности оценки параметров регрессии становятся смещенными.
16. При наличии гетероскедастичности следует применять:
17. Фиктивные переменные – это:
а) атрибутивные признаки (например, как профессия, пол, образование), которым придали цифровые метки;
18. Если качественный фактор имеет три градации, то необходимое число фиктивных переменных:
Эффективность оценки параметра регрессии полученной по мнк означает
2.3. Статистические свойства оценок метода наименьших квадратов
Поскольку полученные оценки a и b коэффициентов линейной регрессии основаны на статистических данных и являются случайными величинами, то естественно установить свойства этих оценок, как случайных величин. Более того, не выяснив этих свойств, невозможно сделать обоснованных выводов относительно качества и надежности полученных оценок. Необходимо, в частности, определить такие их статистические характеристики, как математическое ожидание и дисперсия. К желательным свойствам оценок относятся также несмещенность и состоятельность. Далее, если бы удалось определить вид распределения (плотности распределения) оценок, можно было бы построить доверительные интервалы для истинных значений параметров регрессии (то есть получить интервальные оценки коэффициентов) и реализовать процедуры проверки гипотез относительно их значений. Важную роль играет также изучение статистических свойств остатков оцененной регрессии.
Все эти задачи можно решить, основываясь на некоторых правдоподобных теоретических предпосылках (гипотезах) модели, выполнение которых на практике подлежит проверке с помощью специально разработанных для этого статистических процедур.
Предположение относительно независимых переменных
Предположения относительно случайной составляющей модели
При выполнении предпосылки относительно переменной x статистические свойства оценок параметров и зависимой переменной, а также остатков, целиком определяются вероятностными свойствами случайной составляющей регрессионной модели. Относительно случайной составляющей в классическом регрессионном анализе предполагают выполнение следующих условий, которые называются условиями Гаусса-Маркова и играют ключевую роль при изучении свойств оценок, полученных по методу наименьших квадратов.
1. Первое условие заключается в том, что математическое ожидание случайной составляющей во всех наблюдениях должно быть равно нулю. Формально это записывается так
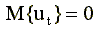 , для всех t =1,2,…,n. , для всех t =1,2,…,n. |
Смысл этого условия заключается в том, что не должно быть систематического смещения случайной составляющей. В линейной регрессии систематическое смещение линии регрессии учитывается с помощью введения параметра смещения 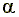
2. Дисперсия случайной составляющей постоянна для всех наблюдений (то есть не зависит от номера наблюдения). Это условие записывается так
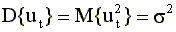 , где дисперсия , где дисперсия 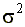 — величина постоянная. — величина постоянная. |
Это свойство дисперсии ошибок называется гомоскедастичностью (однородностью) (запомните этот термин).
Графическая иллюстрация понятий гомоскедастичность и гетероскедастичность
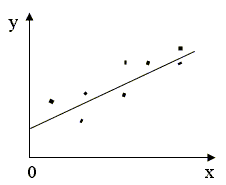
Рис. 2.6а. Гомоскедастичность
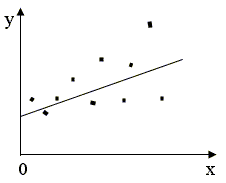
Рис. 2.6б. Гетероскедастичность
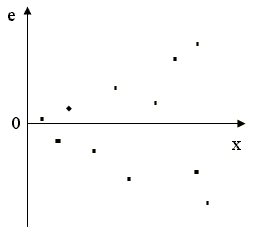
Рис. 2.6в. Гетероскедастичность
3. Случайные составляющие модели для различных наблюдений некоррелированы. Это условие записывается таким образом
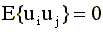 , для всех i не равных j (i, j=1,2,…,n). , для всех i не равных j (i, j=1,2,…,n). |
Выполнение этого условия означает отсутствие систематической (статистической) связи между значениями случайного члена в любых двух наблюдениях. Это свойство на практике также проверяется с помощью статистических процедур на основе анализа остатков модели. Если оно нарушается, то процедура оценки параметров должна быть скорректирована.
4. Четвертое условие Гаусса-Маркова записывается так
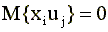 , для всех i и j, , для всех i и j, |
и означает, что объясняющие переменные и случайные составляющие некоррелированы для всех наблюдений. Ранее мы предположили, что объясняющая переменная в модели не является стохастической. В этом случае четвертое условие выполняется автоматически.
Дополнительное предположение о нормальном распределении ошибок
Данное предположение является, пожалуй, наиболее спорным. Дело в том, что предположение о нормальности можно считать правдоподобным, если значения случайной величины порождаются в результате воздействия большого количества независимых случайных факторов, каждый из которых не обязательно имеет нормальное распределение. Примером такого воздействия является так называемое броуновское движение (хаотичное движение малых частиц в жидкости как результат совокупного воздействия на частицу (ударов, соударения) большого количества молекул жидкости).
Если случайные величины в модели распределены по нормальному закону, то из свойств некоррелированности в третьем и четвертом условиях Гаусса-Маркова следует и независимость соответствующих случайных величин.
2.3.2. Свойства выборочных вариаций и ковариаций. Остаточные ошибки (остатки) модели, их свойства
Свойства выборочных вариаций (дисперсий) и ковариаций
Для дальнейшего изложения нам понадобиться установить ряд правил, которые можно использовать при преобразовании выражений, содержащих выборочные вариации и ковариации.
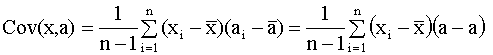 , , |
откуда следует свойство
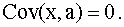
Далее, нетрудно видеть, что имеют место равенства
17. Эффективность МНК-оценок МНК
17. Эффективность МНК-оценок МНК
Свойство эффективности оценок неизвестных параметров модели регрессии, полученных методом наименьших квадратов, доказывается с помощью теоремы Гаусса-Маркова.
Сделаем следующие предположения о модели парной регрессии:
1) факторная переменная xi– неслучайная или детерминированная величина, которая не зависит от распределения случайной ошибки модели регрессии ?i;
2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:
3) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:;
4) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т. е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю):
Это условие выполняется в том случае, если исходные данные не являются временными рядами;
Если выдвинутые предположения справедливы, то оценки неизвестных параметров модели парной регрессии, полученные методом наименьших квадратов, имеют наименьшую дисперсию в классе всех линейных несмещённых оценок, т. е. МНК-оценки можно считать эффективными оценками неизвестных параметров ?0 и ?1.
Если выдвинутые предположения справедливы для модели множественной регрессии, то оценки неизвестных параметров данной модели регрессии, полученные методом наименьших квадратов, имеют наименьшую дисперсию в классе всех линейных несмещённых оценок, т. е. МНК-оценки можно считать эффективными оценками неизвестных параметров ?0…?n.
Для обозначения дисперсий МНК-оценок неизвестных параметров модели регрессии используется матрица ковариаций.
Матрицей ковариаций МНК-оценок параметров линейной модели парной регрессии называется выражение вида:
– дисперсия МНК-оценки параметра модели регрессии ?0;
– дисперсия МНК-оценки параметра модели регрессии ?1.
Матрицей ковариаций МНК-оценок параметров линейной модели множественной регрессии называется выражение вида:
где G2(?) – это дисперсия случайной ошибки модели регрессии ?.
Для линейной модели парной регрессии дисперсии оценок неизвестных параметров определяются по формулам:
2) дисперсия МНК-оценки коэффициента модели регрессии ?1:
где G2(?) – дисперсия случайной ошибки уравнения регрессии ?;
G2(x) – дисперсия независимой переменой модели регрессии х;
n – объём выборочной совокупности.
В связи с тем, что на практике значение дисперсии случайной ошибки модели регрессии G2(?) неизвестно, для вычисления матрицы ковариаций МНК-оценок применяют оценку дисперсии случайной ошибки модели регрессии S2(?).
Для линейной модели парной регрессии оценка дисперсии случайной ошибки определяется по формуле:
– это остатки регрессионной модели, которые рассчитываются как
Тогда оценка дисперсии МНК-оценки коэффициента ?0 линейной модели парной регрессии будет определяться по формуле:
Оценка дисперсии МНК-оценки коэффициента ?1линейной модели парной регрессии будет определяться по формуле:
Для модели множественной регрессии общую формулу расчёта матрицы ковариаций МНК-оценок коэффициентов на основе оценки дисперсии случайной ошибки модели регрессии можно записать следующим образом:
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
Эффективность капитальных вложений
9.1.3. Планирование и эффективность рекламы
9.1.3. Планирование и эффективность рекламы Основной источник разработки стратегии рекламной кампании – общая программа маркетинга. Исходя из этого и формируются цели рекламной кампании. То есть от того, каким путем спланированы все мероприятия по стимулированию сбыта,
12. Эффективность логистической системы
12. Эффективность логистической системы Ученые в области логистики считают, что на данный момент не существует универсальной модели оценки эффективности логистической системы способной учитывать все переменные, все нюансы и все возможные ситуации.Тем не менее один
21. Эффективность закупочной деятельности
21. Эффективность закупочной деятельности Основу экономической эффективности закупочной логистики составляют поиск необходимых материалов удовлетворительного качества и закупка их по минимальным ценам. Вопрос цен – главный в изучении рынка, проводимом
16. Состоятельность и несмещённость МНК-оценок
16. Состоятельность и несмещённость МНК-оценок Предположим, что методом наименьших квадратов получена оценка Для того, чтобы данная оценка могла быть принята за оценку параметра необходимо и достаточно выполнения трёх статистических свойств:1) свойства несмещённости;2)
Эффективность движений
Эффективность движений При выполнении «10 шагов» вы совершаете только те движения, которые помогают байку повернуть. Такие методики «эффективных движений» хорошо знакомы профессиональным танцорам и бойцам. Я впервые познакомился с ними, когда стал заниматься боевыми
27. ЭФФЕКТИВНОСТЬ МАРКЕТИНГА
27. ЭФФЕКТИВНОСТЬ МАРКЕТИНГА Критерии оценкиОценивать эффективность отдельных методов комплекса маркетинга по конечным результатам, например росту объема продаж, чрезвычайно сложно. Поэтому часто используется относительная оценка, когда стоимость того или иного
Эффективность и рациональность
Эффективность и рациональность Как говорил Сенека, когда не знаешь, в какую гавань держишь путь, ни один ветер не будет дуть в нужном направлении. Для организации операционная стратегия заключается в точном определении своей деятельности, т. е. что является центральной
Эффективность
Эффективность Эффективность E, согласно ISO 9000, – это соотношение достигнутого эффекта (результата) Q и затраченных ресурсов C:E = Q / C (4.4)Эффективность
4.3. Эффективное время, Эффективность
4.3. Эффективное время, Эффективность Не зря до сих пор специалисты в экономике, как только речь идет о точном расчете эффективности, не могут прийти к единому мнению, ибо в конкретном деле такие факторы, как социальные, личностные и другие не могут быть точно выражены в
Множественная регрессия и корреляция
Множественная регрессия и корреляция
1. Добавление в уравнение множественной регрессии новой объясняющей переменной:
а) уменьшает значение коэффициента детерминации;
б) увеличивает значение коэффициента детерминации;
в) не оказывает никакого влияние на коэффициент детерминации ■
Скорректированный коэффициент детерминации:
а) меньше обычного коэффициента детерминации;
б) больше обычного коэффициента детерминации;
в) меньше или равен обычному коэффициенту детерминации;
С увеличением числа объясняющих переменных скорректированный коэффициент детерминации:
Число степеней свободы для остаточной суммы квадратов в линейной модели множественной регрессии равно:
Число степеней свободы для общей суммы квадратов в линейной модели множественной регрессии равно:
Число степеней свободы для факторной суммы квадратов в линейной модели множественной регрессии равно:
Множественный коэффициент корреляции R>xiX2 = 0,9. Определите, какой процент дисперсии зависимой переменной у объясняется влиянием факторов x1 и x2:
Для построения модели линейной множественной регрессии
вида у = a + b x1 + b2 x2 необходимое количество наблюдений должно быть не менее:
Стандартизованные коэффициенты регрессии Д:
а) позволяют ранжировать факторы по силе их влияния на
б) оценивают статистическую значимость факторов;
в) являются коэффициентами эластичности.
Частные коэффициенты корреляции:
а) характеризуют тесноту связи рассматриваемого набора факторов
с исследуемым признаком;
б) содержат поправку на число степеней свободы и не допускают
преувеличения тесноты связи;
в) характеризуют тесноту связи между результатом и
соответствующим фактором при элиминировании других факторов,
включенных в уравнение регрессии.
а) оценивает значимость уравнения регрессии в целом;
б) служит мерой для оценки включения фактора в модель;
в) ранжирует факторы по силе их влияния на результат.
Несмещенность оценки параметра регрессии, полученной по МНК, означает:
а) что она характеризуется наименьшей дисперсией;
б) что математическое ожидание остатков равно нулю;
в) увеличение ее точности с увеличением объема выборки.
Эффективность оценки параметра регрессии, полученной по МНК, означает:
а) что она характеризуется наименьшей дисперсией;
б) что математическое ожидание остатков равно нулю;
в) увеличение ее точности с увеличением объема выборки.
Состоятельность оценки параметра регрессии, полученной по МНК, означает:
а) что она характеризуется наименьшей дисперсией;
б) что математическое ожидание остатков равно нулю;
в) увеличение ее точности с увеличением объема выборки.
Укажите истинное утверждение:
а) скорректированный и обычный коэффициенты множественной
детерминации совпадают только в тех случаях, когда обычный
коэффициент множественной детерминации равен нулю;
б) стандартные ошибки коэффициентов регрессии определяются
значениями всех параметров регрессии;
в) при наличии гетероскедастичности оценки параметров регрессии
При наличии гетероскедастичности следует применять:
в) метод максимального правдоподобия.
Фиктивные переменные это:
а) атрибутивные признаки (например, как профессия, пол,
образование), которым придали цифровые метки;
б) экономические переменные, принимающие количественные
значения в некотором интервале;
в) значения зависимой переменной за предшествующий период
18. Если качественный фактор имеет три градации, то необходимое число фиктивных переменных:
Системы эконометрических уравнений
Наибольшее распространение в эконометрических исследованиях получили:
а) системы независимых уравнений;
б) системы рекурсивных уравнений;
в) системы взаимозависимых уравнений.
Эндогенные переменные это:
а) предопределенные переменные, влияющие на зависимые
переменные, но не зависящие от них, обозначаются через x.;
б) зависимые переменные, число которых равно числу уравнений в
системе и которые обозначаются через у ;
в) значения зависимых переменных за предшествующий период
Экзогенные переменные это:
а) предопределенные переменные, влияющие на зависимые
переменные, но не зависящие от них, обозначаются через x;
б) зависимые переменные, число которых равно числу уравнений в
системе и которые обозначаются через у ;
в) значения зависимых переменных за предшествующий период
Лаговые переменные это:
а) предопределенные переменные, влияющие на зависимые переменные, но не зависящие от них, обозначаются через x.;
б) зависимые переменные, число которых равно числу уравнений в
системе и которые обозначаются через у;
в) значения зависимых переменных за предшествующий период
Для определения параметров структурную форму модели необходимо преобразовать в:
а) приведенную форму модели;
б) рекурсивную форму модели;
в) независимую форму модели.
Модель идентифицируема, если:
а) число приведенных коэффициентов меньше числа структурных
б) если число приведенных коэффициентов больше числа
в) если число параметров структурной модели равно числу
параметров приведенной формы модели.
Модель неидентифицируема, если:
а) число приведенных коэффициентов меньше числа структурных
б) если число приведенных коэффициентов больше числа
в) если число параметров структурной модели равно числу
параметров приведенной формы модели.
Модель сверхидентифицируема, если:
а) число приведенных коэффициентов меньше числа структурных
б) если число приведенных коэффициентов больше числа
в) если число параметров структурной модели равно числу
параметров приведенной формы модели.
Уравнение идентифицируемо, если:
Уравнение неидентифицируемо, если:
Уравнение сверхидентифицируемо, если:
Для определения параметров точно идентифицируемой модели:
а) применяется двушаговый МНК;
б) применяется косвенный МНК;
б) ни один из существующих методов применить нельзя.
Для определения параметров сверхидентифицируемой модели:
а) применяется двушаговый МНК;
б) применяется косвенный МНК;
б) ни один из существующих методов применить нельзя.
Для определения параметров неидентифицируемоймодели:
а) применяется двушаговый МНК;
б) применяется косвенный МНК;
б) ни один из существующих методов применить нельзя.
1. Аддитивная модель временного ряда имеет вид:
Мультипликативная модель временного ряда имеет вид:
а) характеризует тесноту линейной связи текущего и предыдущего
б) характеризует тесноту нелинейной связи текущего и
предыдущего уровней ряда;
в) характеризует наличие или отсутствие тенденции.
Аддитивная модель временного ряда строится, если:
а) значения сезонной компоненты предполагаются постоянными
для различных циклов;
б) амплитуда сезонных колебаний возрастает или уменьшается;
в) отсутствует тенденция.
Мультипликативная модель временного ряда строится, если:
а) значения сезонной компоненты предполагаются постоянными
для различных циклов;
б) амплитуда сезонных колебаний возрастает или уменьшается;
в) отсутствует тенденция.
Критерий Дарбина-Уотсона применяется для:
а) определения автокорреляции в остатках;
б) определения наличия сезонных колебаний;
в) для оценки существенности построенной модели.
Вопросы к экзамену
L Определение эконометрики Эконометрический метод и этапы эконометрического исследования ■
2^ Парная регрессия^ Способы задания уравнения парной регрессии
3^ Линейная модель парной регрессии Смысл и оценка параметров ■
4^ Оценка существенности уравнения в целом и отдельных его параметров (F-критерий Фишера и t-критерий Стьюдента)■
5^ Прогноз по линейному уравнению регрессии Средняя ошибка аппроксимации ■
6^ Нелинейная регрессия^ Классы нелинейных регрессий
7^ Регрессии нелинейные относительно включенных в анализ объясняющих переменных^
8^ Регрессии нелинейные по оцениваемым параметрам ■
9^ Коэффициенты эластичности для разных видов регрессионных моделей ■
10^ Корреляция и F-критерий Фишера для нелинейной регрессии
1L Отбор факторов при построении уравнения множественной регрессии
12^ Оценка параметров уравнения множественной регрессии
13^ Множественная корреляция^
14^ Частные коэффициенты корреляции
16^ t-критерий Стьюдента для уравнения множественной регрессии
Фиктивные переменные во множественной регрессии.
Предпосылки МНК: гомоскедастичность и
Предпосылки МНК: автокорреляция остатков.
Общие понятия о системах эконометрических уравнений.
Структурная и приведенная формы модели.
Проблема идентификации. Необходимое условие идентифицируемости.
Проблема идентификации. Достаточное условие идентифицируемости.
Методы оценки параметров структурной формы модели.
Основные элементы временного ряда.
Автокорреляция уровней временного ряда и выявление его структуры.
Моделирование сезонных колебаний: аддитивная модель временного ряда.
Моделирование сезонных колебаний: мультипликативная модель временного ряда.
Приложение D Варианты индивидуальных заданий D.1. Парная регрессия и корреляция
Пример. По территориям региона приводятся данные за 199X г.

Рассчитать линейный коэффициент парной корреляции, коэффициент детерминации и среднюю ошибку аппроксимации.
4. Выполнить прогноз заработной платы y при прогнозном
значении среднедушевого прожиточного минимума x, составляющем 107\% от среднего уровня.
5. Оценить точность прогноза, рассчитав ошибку прогноза и его
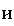 |
6. На одном графике отложить исходные данные теоретическую прямую.
уравнения линейной регрессии
1. Для расчета параметров строим расчетную таблицу D.2.