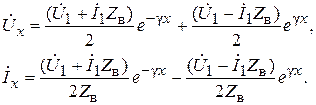электрические цепи с распределенными параметрами общие сведения уравнения однородной линии

302_toe / ТОЭ 3 / Лекция №36

13. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

13.1. Понятие об электрических цепях с распределенными параметрами

Строго говоря, всегда параметры электрической цепи в той или иной степени распределены вдоль ее участков, и только абстрагируясь от действительности можно предполагать, что такие параметры цепи как активное сопротивление – R, индуктивность – L и емкость – C сосредоточены в ее определенных участках. Во многих случаях такое допущение не приводит к существенным ошибкам в результатах проводимого анализа. Ранее мы имели дело с цепями с сосредоточенными параметрами. Однако, такой подход не всегда возможен. Например, рассматривая электромагнитные процессы, происходящие в электрических линиях, при помощи которых электрическая энергия или сигналы передаются на расстояние, необходимо иметь ввиду, что электрические и магнитные поля распределены по всей длине линии, и превращение электрической энергии в тепло также происходит по всей длине линии. Критерием необходимости рассматривать цепь в качестве цепи с распределенными параметрами является то, что интервал времени распространения электромагнитной волны вдоль всей цепи и интервал времени, в течение которого токи и напряжения меняются на заметную величину, должны быть соизмеримыми.

Токи напряжения в таких цепях являются функциями двух независимых переменных: времени – t и расстояния – x, отсчитываемого вдоль направления цепи. Уравнения, описывающие процессы в таких цепях, являются уравнениями в частных производных. Примерами являются линии передачи электрической энергии, линии связи, антенные вводы радиотехнических устройств, обмотки электрических машин при воздействии на них импульсных токов и напряжений.

Параметры цепи могут быть распределены неравномерно вдоль линии.

Однако во многих случаях этим можно пренебречь и считать параметры равномерно распределенными. Такие линии называются однородными.

В дальнейшем под величинами R, L, C, G, M будем понимать активное сопротивление, индуктивность и т.д., приходящиеся на единицу длины, и будем обозначать их через R₀, L₀, C₀, G₀, M₀. В общем случае эти параметры зависят от частоты, например, увеличение активного сопротивления и индуктивности с ростом частоты вследствие поверхностного эффекта. Однако для простоты в дальнейшем это учитывать не будем.

13.2. Уравнения линии с распределенными параметрами

Напряжения и ток в линии являются функциями двух независимых переменных – пространственной координаты x, определяющей место наблюдения, и времени t, определяющей момент наблюдения. Считается, что направление координаты x совпадает с осью линии.

Необходимо найти пространственно-временное распределение величины тока в линии i(x, t) и напряжения между проводами u(x, t). В этом случае также можно определить процесс передачи энергии по линии, когда приемники и источники находятся на обоих концах линии.

Приняв положительное направление тока в линии слева направо, условимся называть «началом» левый конец линии. Расстояние от начальной точки до произвольной обозначим через x, а от конца – через x‘. Вся длина линии l = x + x‘.

Выделим элементарный участок x на расстоянии x от начала. Пользуясь первичными параметрами R₀, L₀, C₀, G₀, отнесенными к единице длины линии, представим приближенно участок x в виде схемы замещения (рис. 13.1).

Источник

5. Электрические цепи с распределенными параметрами

5.1. Основные определения

В этом разделе будем рассматривать длинные линии или цепи, сводящиеся к длинным линиям.

Электрическими линиями с распределенными параметраминазы­вают такие линии, в которых для одного и того же момента времени ток и напряжение непрерывно изменяются при переходе от одной точки (сечения) линии к другой, соседней точке.

Под магнитными линиями с распределенными параметрамипони­мают такие линии, магнитный поток и магнитное напряжение вдоль которых непрерывно меняются при переходе от одной точки линии к соседней.

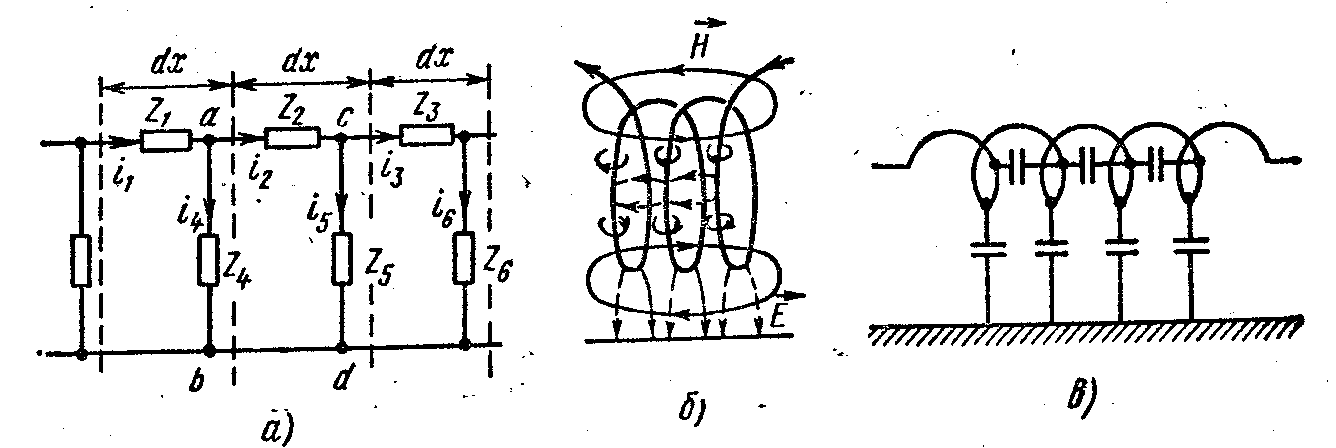
Эффект непрерывного изменения тока (потока) и электрического (магнитного) напряжения вдоль линии существует вследствие того, что линии обладают распределенными продольными и поперечными сопротивлениями (рис. 5.1, а).

На схеме (рис. 5.1, а) изображен участок линии с распределен­ными параметрами, через dxобозначен бесконечно малый элемент длины линии.

В результате утечки тока через сопротивление Z₄ток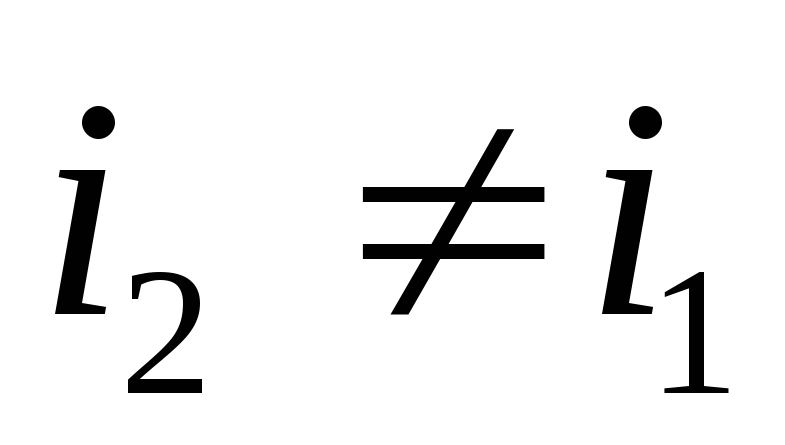. Аналогично, токи т. д. Напряжение между точкамиаиb не равно напряжению между точкамисиd и т. д.

В электрических линиях с распределенными параметрами продоль­ные сопротивления образованы активными сопротивлениями проводов линии и индуктивностями двух противостоящих друг другу участков линии длиной dx.Поперечные сопротивления состоят из сопротивле­ний утечки, появляющейся вследствие несовершенства изоляции между проводами линии, и емкостей, образованных противостоящими друг другу элементами (участками) линии. В магнитных линиях с рас­пределенными параметрами продольные сопротивления представляют собой магнитные сопротивления самих магнитных стержней, образую­щих магнитную линию, а поперечные сопротивления обусловлены утечкой магнитного потока по воздуху между противостоящими друг другу участками линии.

Линию с распределенными параметрами называют однородной,если равны друг другу все продольные сопротивления участков линии одинаковой длины и если равны друг другу все поперечные сопро­тивления участков линии одинаковой длины. Так, участок линии (рис. 5.1,а) однороден, еслиZ₁ = Z₂ =Z₃ =. иZ₄ =Z₅ =Z₆.

Линию с распределенными параметрами называют неоднородной, если продольные сопротивления в ней различны или поперечные сопротивления неодинаковы.

Кроме того, линии с распределенными параметрами можно под­разделить на две большие группы: нелинейные и линейные.

В качестве примера нелинейной электрической линии с распреде­ленными параметрами можно назвать электрическую линию передачи высокого напряжения при наличии между проводами линии тихого электрического разряда—явления короны на проводах. В этом слу­чае емкость между противостоящими друг другу участками линии является функцией напряжения между этими участками.

В качестве примера нелинейной магнитной линии с распределен­ными параметрами можно назвать линию, образованную параллельно расположенными магнитными сердечниками, которые в процессе работы линии могут насыщаться.

Когда говорят о линии с распределенными параметрами, то обычно этот термин мысленно связывают с мощными линиями передачи элек­трической энергии на большие расстояния, с телефонными и телеграф­ными воздушными или кабельными линиями, с рельсовыми линиями автоблокировки на железнодорожном транспорте, с антеннами в ра­диотехнике и другими родственными линиями и установками.

В то же время с линиями с распределенными параметрами имеют дело и тогда, когда «линий» в буквальном смысле слова, казалось бы, вовсе нет. Так, обычная индуктивная катушка при достаточно высо­ких частотах представляет собой линию с распределенными парамет­рами (рис. 5.1,б). Из рисунка (рис.5.1,в) видно, что кроме индуктивностей в схеме замещения есть межвитковые емкости и емкости на корпус прибора (на землю).

Если по катушке проходит переменный ток, то через межвитко­вые емкости и емкости на землю также идет ток. При одном и том же напряжении между соседними витками ток через емкости тем больше, чем выше частота переменного тока. При низкой частоте (десятки, сотни, тысячи герц) ток через емкости несоизмеримо мал по сравнению с токами через витки катушки и наличие емкостей можно не учитывать в расчете (что и делалось до сих пор). Если же частота тока очень велика, например сотни миллиардов герц, то токи через емкости могут во много раз превышать токи через витки катушки. В этом случае вся катушка в целом будет оказывать прохождению переменного тока емкостное, а не индуктивное сопротивление (коли­чественные изменения перешли в качественные). При промежуточных частотах порядка нескольких мегагерц (когда линейные размеры ка­тушки соизмеримы с длиной волны) индуктивная катушка является типичной линией с распределенными параметрами. Если индуктивная катушка намотана на стальной сердечник, который способен насы­щаться и частота тока достаточно велика, то все устройство в целом представляет собой сложную совокупность из электрической и маг­нитной нелинейных цепей с распределенными параметрами.

В курсе ТОЭ изучают только основы однородных линейных цепей с распределенными параметрами. Вся теория излагается применительно к электрическим линиям с распределенными параметрами на перемен­ном токе. Теория однородных линейных электрических цепей с рас­пределенными параметрами на постоянном токе непосредственно сле­дует из теории цепей переменного тока, если принять угловую частоту равной нулю.

Теория однородных линейных магнитных линий на постоянном токе в значительной мере аналогична теории однородных линейных электрических линий с распределенными параметрами, только вместо тока в уравнении должен быть подставлен магнитный поток, вместо электрического напряжения — маг­нитное напряжение, вместо продоль­ного активного сопротивления — продольное магнитное сопротивле­ние, вместо поперечной электриче­ской проводимости — поперечная магнитная проводимость.

Источник

5.1. Электрические цепи с распределенными параметрами основные определения

В этом разделе будем рассматривать длинные линии или цепи, сводящиеся к длинным линиям.

Электрическими линиями с распределенными параметрами назы­вают такие линии, в которых для одного и того же момента времени ток и напряжение непрерывно изменяются при переходе от одной точки (сечения) линии к другой, соседней точке.

Под магнитными линиями с распределенными параметрами пони­мают такие линии, магнитный поток и магнитное напряжение вдоль которых непрерывно меняются при переходе от одной точки линии к соседней.

Эффект непрерывного изменения тока (потока) и электрического (магнитного) напряжения вдоль линии существует вследствие того, что линии обладают распределенными продольными и поперечными сопротивлениями (рис. 5.1, а).

На схеме (рис. 5.1, а) изображен участок линии с распределен­ными параметрами, через dx обозначен бесконечно малый элемент длины линии.

В результате утечки тока через сопротивление Z ₄ ток . Аналогично, ток и т.д. Напряжение между точками а и b не равно напряжению между точками с и d и т.д.

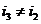
В электрических линиях с распределенными параметрами продоль­ные сопротивления образованы активными сопротивлениями проводов линии и индуктивностями двух противостоящих друг другу участков линии длиной dx. Поперечные сопротивления состоят из сопротивле­ний утечки, появляющейся вследствие несовершенства изоляции между проводами линии, и емкостей, образованных противостоящими друг другу элементами (участками) линии. В магнитных линиях с рас­пределенными параметрами продольные сопротивления представляют собой магнитные сопротивления самих магнитных стержней, образую­щих магнитную линию, а поперечные сопротивления обусловлены утечкой магнитного потока по воздуху между противостоящими друг

другу участками линии.

Линию с распределенными параметрами называют однородной, если равны друг другу все продольные сопротивления участков линии одинаковой длины и если равны друг другу все поперечные сопро­тивления участков линии одинаковой длины. Так, участок линии (рис. 5.1, а) однороден, если Z ₁ = Z ₂ = Z ₃ =… и Z ₄ = Z ₅ = Z ₆.

Линию с распределенными параметрами называют неоднородной, если продольные сопротивления в ней различны или поперечные сопротивления неодинаковы.

Кроме того, линии с распределенными параметрами можно под­разделить на две большие группы: нелинейные и линейные.

В качестве примера нелинейной электрической линии с распреде­ленными параметрами можно назвать электрическую линию передачи высокого напряжения при наличии между проводами линии тихого электрического разряда – явления короны на проводах. В этом слу­чае емкость между противостоящими друг другу участками линии является функцией напряжения между этими участками.

В качестве примера нелинейной магнитной линии с распределен­ными параметрами можно назвать линию, образованную параллельно расположенными магнитными сердечниками, которые в процессе работы линии могут насыщаться.

Когда говорят о линии с распределенными параметрами, то обычно этот термин мысленно связывают с мощными линиями передачи элек­трической энергии на большие расстояния, с телефонными и телеграф­ными воздушными или кабельными линиями, с рельсовыми линиями автоблокировки на железнодорожном транспорте, с антеннами в ра­диотехнике и другими родственными линиями и установками.

В то же время с линиями с распределенными параметрами имеют дело и тогда, когда «линий» в буквальном смысле слова, казалось бы, вовсе нет. Так, обычная индуктивная катушка при достаточно высо­ких частотах представляет собой линию с распределенными парамет­рами (рис. 5.1, б). Из рисунка (рис. 5.1, в) видно, что кроме индуктивностей в схеме замещения есть межвитковые емкости и емкости на корпус прибора (на землю).

Если по катушке проходит переменный ток, то через межвитко­вые емкости и емкости на землю также идет ток. При одном и том же напряжении между соседними витками ток через емкости тем больше, чем выше частота переменного тока. При низкой частоте (десятки, сотни, тысячи герц) ток через емкости несоизмеримо мал, по сравнению с токами через витки катушки, и наличие емкостей можно не учитывать в расчете (что и делалось до сих пор).

Если же частота тока очень велика, например сотни миллиардов герц, то токи через емкости могут во много раз превышать токи через витки катушки. В этом случае вся катушка в целом будет оказывать прохождению переменного тока емкостное, а не индуктивное сопротивление (коли­чественные изменения перешли в качественные).

При промежуточных частотах, порядка нескольких мегагерц (когда линейные размеры ка­тушки соизмеримы с длиной волны), индуктивная катушка является типичной линией с распределенными параметрами.

Если индуктивная катушка намотана на стальной сердечник, который способен насы­щаться, и частота тока достаточно велика, то все устройство в целом представляет собой сложную совокупность из электрической и маг­нитной нелинейных цепей с распределенными параметрами.

В курсе ТОЭ изучают только основы однородных линейных цепей с распределенными параметрами. Вся теория излагается применительно к электрическим линиям с распределенными параметрами на перемен­ном токе. Теория однородных линейных электрических цепей с рас­пределенными параметрами на постоянном токе непосредственно сле­дует из теории цепей переменного тока, если принять угловую частоту равной нулю.

Теория однородных линейных магнитных линий на постоянном токе в значительной мере аналогична теории однородных линейных электрических линий с распределенными параметрами, только вместо тока в уравнении должны быть подставлены:

Источник

ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

Общие сведения

Цепями с распределенными параметрами называются идеализированные электрические цепи, процессы в которых описываются дифференциальными уравнениями в частных производных. Это связано с тем, что если длина волны λ электромагнитных колебаний соизмерима с размерами цепи l, то токи и напряжения в этой одномерной цепи являются функциями двух переменных – времени t и координаты x – u(t, x), i(t, x).

Исторически первыми в качестве одномерных цепей с распределенными параметрами стали представлять так называемые длинные линии, т.е. двухпроводные линии передачи сигнала от источника к нагрузке (рис. 6. 1), длина которых l значительно превышает длину волны λ передаваемых электромагнитных колебаний. Поэтому часто эти цепи называют длинными линиями или линиями. При этом будем полагать, что конструктивные данные линии (материал и диаметр ее проводов, их взаимное расположение) и ее параметры сохраняются неизменными по длине линии. Такие длинные линии называются однородными.

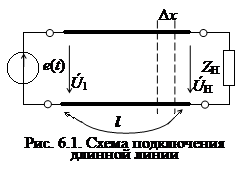
Задача анализа цепей с распределенными параметрами обычно сводится к определению законов (характера) изменения токов и напряжений вдоль цепи и к исследованию частотных и временных характеристик цепи. С этой целью следует рассмотреть электрическую модель отрезка линии малой длины Δx = dx. Эта модель с достаточной точностью исследования может быть представлена электрической цепью с сосредоточенными параметрами (рис. 6.2). Всю линию можно представить как цепи с бесконечно большим числом малых по величине пассивных элементов, распределенных равномерно по ее длине.

На основании физических рассуждений можно составить следующую эквивалентную схему отрезка (рис. 6.2).

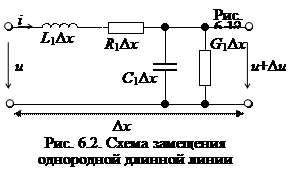
При прохождении тока вокруг проводника образуется внешнее магнитное поле, которое можно моделировать индуктивностью L₀. Она препятствует прохождению тока. Вместе с этим проводник обладает сопротивлением материала R₀. Следовательно, эти элементы должны быть соединены последовательно.

Проводники объединены конструктивно диэлектриком, который обладает конечной резистивной проводимостью G₀. Между проводниками линии создается разность потенциалов. Следовательно, вокруг проводников существует электрическое поле, накопление которого моделируется емкостью С₀.

Элементы L₀, C₀, R₀, G₀ называются параметрами линии (отрезка линии). Однако каждый отрезок линии имеет конечную длину Dx, поэтому вводятся понятия погонных параметров:

Входное сопротивление линии

Входное сопротивление линии определяется отношением напряжения и тока в начале линии. Найдем выражение входного сопротивления

используя уравнения (6.11)

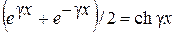
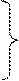
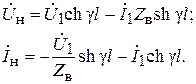
Если учесть, что и и принять при x = l Ú_x = Ú_н и Ì_x = Ì_н, то система уравнений (6.11) примет вид

(6.28)

Разрешая эту систему уравнений относительно напряжения Ú₁ и тока Ì₁, получим

(6.29)

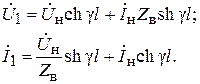
Используя уравнения (6.29), получим выражение входного сопротивления

(6.30)

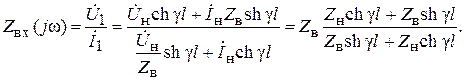
Рассмотрим некоторые частные режимы работы линии.

1. При согласованном включении линии (Z_н = Z_в) из (6.30) получим, что

2. Если выходные зажимы линии замкнуты накоротко (Z_н = 0), то формула (6.30) упрощается:

(6.31)

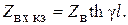
3. В случае разомкнутых выходных зажимов (Z_н = ∞)

(6.32)

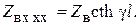
4. Когда линия нагружена на произвольное сопротивление, не равное волновому (Z_н ≠ Z_в), можно пользоваться для расчетов не только формулой (6.30), но и более удобной. Для этого разделим числитель и знаменатель в (6.30) на ch γl:

.

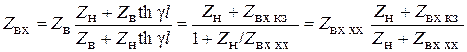
Линия без потерь

Вторичные параметры и уравнения передачи. Реальная линия всегда обладает потерями. Однако в ряде случаев удобно считать линию идеальной, т. е. не имеющей потерь: R₁ = G₁ = 0. Такая идеализация оправдана для коротких по длине линий, работающих на сверхвысоких частотах (фидеров, элементов радиотехнических устройств, полосковых линий и др.), где выполняются условия R₁ 0 амплитуды убывают в сторону нагрузки). Сдвиг фаз между напряжением u_x и током i_x равен нулю, поэтому энергия бегущей волны носит активный характер. Следовательно, в режиме бегущих волн передача энергии в линии производится только в одном направлении – от источника энергии к нагрузке. Вся энергия, предаваемая падающей волной, потребляется нагрузкой. Этот режим используется для передачи сигнала от источника в нагрузку.

Входное сопротивление из (6.35) равно волновому сопротивлению Z_ВХ = R₀.

Режим стоячих волн. Как было сказано ранее, что если модуль коэффициента отражения линии │p(x)│ ≡ 1, т. е. амплитуды отраженной и падающей волн во всех сечениях линии одинаковы, то в линии устанавливается специфический режим, называемый режимом стоячих волн. Это равенство амплитуд возможно только в линии без потерь (α = 0) т. е. │p_н│ = 1.

Анализируя выражение (6.23) 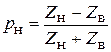, можно убедиться, что │p_н│ = 1 только в трех случаях: Z_н = 0, либо Z_н = ∞, либо Z_н = jx.

Следовательно, режим стоячих волн может установиться только в линии без потерь при коротком замыкании или холостом ходе на выходе, а также если сопротивление нагрузки имеет чисто реактивный характер.

Короткое замыкание линии КЗ. При Z_н = 0 напряжение в конце линии равно нулю Ú_н = 0. Уравнения передачи (6.34) для данного режима принимают вид:

(6.36)

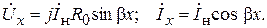
Если положить для простоты начальную фазу тока в конце линии равной нулю φi_н = 0, то мгновенные значения напряжения и тока в любой точке линии описываются выражениями:

(6.37)

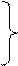
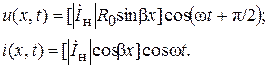
Выражения (6.37) показывают, что при коротком замыкании на выходе линии амплитуды напряжения и тока изменяются вдоль линии по периодическому (гармоническому) закону

,

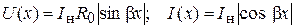
принимая в отдельных точках линии максимальные значения U_max =R₀I_н, I_н = I_max и обращаются в нуль в некоторых других точках (рис. 6.6).

Точки, в которых амплитуда (мгновенные значения) напряжения (тока) тождественно равны нулю, называются узлами напряжения (тока).

Характерные точки, в которых амплитуда (мгновенные значения) напряжения (тока) принимают максимальное значение, называются пучностями напряжения (тока). Как видно из рис. 6.6, узлы напряжения соответствуют пучностям тока и, наоборот, узлы тока соответствуют пучностям напряжения.

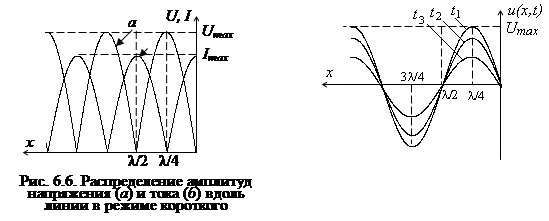Распределение мгновенных значений напряжения (рис. 6.7) (тока) вдоль линии гармоническому закону, однако с течением времени координаты точек, имеющих одинаковую фазу, остаются неизменными, т. е. волны напряжения (тока) как бы «стоят на месте». Именно поэтому такой режим работы линии получил название режима стоячих волн.

Координаты узлов напряжения определяются из условия sinβx_k = 0, откуда при β = 2π/π

где k = 0, 1, 2, …, а координаты пучностей напряжения – из условия cosβx_k = 0, откуда

Пучности возникают в тех сечениях линии, в которых падающая и отраженная волны напряжения (тока) совпадают по фазе и, следовательно, суммируются, а узлы располагаются в сечениях, где падающая и отраженная волны напряжения (тока) находятся в противофазе и, следовательно, вычитаются.

Мгновенная мощность в узлах напряжения и тока в любой момент времени равна нулю.

Таким образом, в режиме стоячих волн энергия вдоль линии не распространяется и на каждом участке линии происходит только обмен энергией между электрическим и магнитным полями. Этот режим не используется для передачи сигнала от источника в нагрузку.

Из (6.36) следует, что входное сопротивление в произвольной точке x линии равно (расстояние x от конца линии)

(6.38)

Из выражения (6.38) следует, что резистивная составляющая комплексного входного сопротивления отрезка линии без потерь а режиме КЗ на выходе равна нулю, а реактивная составляющая

является периодической функцией электрической длины x/λ и может принимать любые значения от – ∞ до ∞ (рис. 6.8).

При x = 0, λ/2, λ, 3λ/2, … величина βx = (2π/λ)x = 0, π, 2π, 3π, … и входное сопротивление Z_{вх кз} = 0. При x = λ/4, 3λ/4, 5λ/4, … величина βx = (2π/λ)x = π/2. и входное сопротивление Z_{вх кз} = ±j∞.

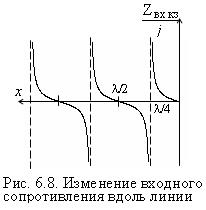
В случае, когда линия нагружена на емкость C_н можно поступить так же, как при индуктивной нагрузке.

Включение линии на произвольное комплексное сопротивление, не равное волновому. Положим для определенности, что сопротивление нагрузки R_н>R₀. Коэффициент отражения на основании (6.23)│p│=(R_н–R₀)/(R_н+R₀)

Источник