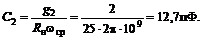элементы с распределенными параметрами

Цепи с распределенными и с сосредоточенными параметрами

Если электрическая цепь содержит хотя бы один элемент с распределенными параметрами, то эта цепь называется цепью с распределенными параметрами. В противном случае цепь с сосредоточенными параметрами.

Элемент с сосредоточенными параметрами – это такой элемент, размеры которого не влияют на физические процессы в нем. К элементам с распределенными параметрами относятся линии передач, антенны. Если размеры элемента влияют на физические процессы, то это элемент с распределенными параметрами. В основном большинство элементов будем считать элементами с сосредоточенными параметрами.

Все высказанные выше определения достаточно условны. Один и тот же элемент в той или иной степени описания процесса на нем может быть отнесен к линейным или нелинейным, с распределенными или сосредоточенными параметрами.

В дальнейшем мы будем изучать линейные цепи с сосредоточенными параметрами.

Электрическая схема

Графическое изображение электрической цепи называется электрической схемой. На электрических схемах различают 3 элемента:

1. Ветвь – это последовательное соединение элементов, по которым протекает один и тот же ток.

2. Узел – это место электрической схемы, где сходится 3 и более ветвей.

3. Контур – это замкнутый участок цепи.

— ветви;

— узлы;

— замкнутые контуры.

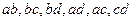
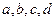
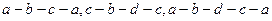
Число независимых контуров – это минимальное количество контуров, из которых может быть составлена рассматриваемая схема.

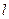
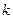
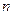
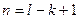
Обозначим — число ветвей, — число узлов, — число независимых контуров, которое определяется по формуле .

Положительные направления токов, падений напряжений и э.д.с.

Обычно при анализе электрических цепей произвольно выбирается положительное направление токов в ветвях. Затем в зависимости от выбранных положительных направлений токов определяются положительные направления 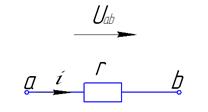падений напряжений на элементах. Рассмотрим отдельные элементы.

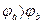
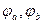
Это значит , — потенциалы точек а и b.

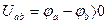
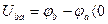
Падение напряжений – это разность потенциалов, т.е. , . То же самое будет на катушке индуктивности и конденсаторе.

Таким образом, положительное направление падения напряжения на пассивных элементах совпадает с положительным направлением тока через них.

Рассмотрим активный элемент – источник э.д.с.

, — потенциалы точек а и b.Тогда , .

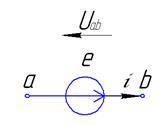
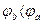
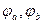
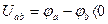
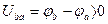
Таким образом, положительное направление падения напряжения на источнике э.д.с. противоположно положительному направлению э.д.с.

Пример:

Источник

5.1. Электрические цепи с распределенными параметрами основные определения

В этом разделе будем рассматривать длинные линии или цепи, сводящиеся к длинным линиям.

Электрическими линиями с распределенными параметрами назы­вают такие линии, в которых для одного и того же момента времени ток и напряжение непрерывно изменяются при переходе от одной точки (сечения) линии к другой, соседней точке.

Под магнитными линиями с распределенными параметрами пони­мают такие линии, магнитный поток и магнитное напряжение вдоль которых непрерывно меняются при переходе от одной точки линии к соседней.

Эффект непрерывного изменения тока (потока) и электрического (магнитного) напряжения вдоль линии существует вследствие того, что линии обладают распределенными продольными и поперечными сопротивлениями (рис. 5.1, а).

На схеме (рис. 5.1, а) изображен участок линии с распределен­ными параметрами, через dx обозначен бесконечно малый элемент длины линии.

В результате утечки тока через сопротивление Z ₄ ток . Аналогично, ток и т.д. Напряжение между точками а и b не равно напряжению между точками с и d и т.д.

В электрических линиях с распределенными параметрами продоль­ные сопротивления образованы активными сопротивлениями проводов линии и индуктивностями двух противостоящих друг другу участков линии длиной dx. Поперечные сопротивления состоят из сопротивле­ний утечки, появляющейся вследствие несовершенства изоляции между проводами линии, и емкостей, образованных противостоящими друг другу элементами (участками) линии. В магнитных линиях с рас­пределенными параметрами продольные сопротивления представляют собой магнитные сопротивления самих магнитных стержней, образую­щих магнитную линию, а поперечные сопротивления обусловлены утечкой магнитного потока по воздуху между противостоящими друг

другу участками линии.

Линию с распределенными параметрами называют однородной, если равны друг другу все продольные сопротивления участков линии одинаковой длины и если равны друг другу все поперечные сопро­тивления участков линии одинаковой длины. Так, участок линии (рис. 5.1, а) однороден, если Z ₁ = Z ₂ = Z ₃ =… и Z ₄ = Z ₅ = Z ₆.

Линию с распределенными параметрами называют неоднородной, если продольные сопротивления в ней различны или поперечные сопротивления неодинаковы.

Кроме того, линии с распределенными параметрами можно под­разделить на две большие группы: нелинейные и линейные.

В качестве примера нелинейной электрической линии с распреде­ленными параметрами можно назвать электрическую линию передачи высокого напряжения при наличии между проводами линии тихого электрического разряда – явления короны на проводах. В этом слу­чае емкость между противостоящими друг другу участками линии является функцией напряжения между этими участками.

В качестве примера нелинейной магнитной линии с распределен­ными параметрами можно назвать линию, образованную параллельно расположенными магнитными сердечниками, которые в процессе работы линии могут насыщаться.

Когда говорят о линии с распределенными параметрами, то обычно этот термин мысленно связывают с мощными линиями передачи элек­трической энергии на большие расстояния, с телефонными и телеграф­ными воздушными или кабельными линиями, с рельсовыми линиями автоблокировки на железнодорожном транспорте, с антеннами в ра­диотехнике и другими родственными линиями и установками.

В то же время с линиями с распределенными параметрами имеют дело и тогда, когда «линий» в буквальном смысле слова, казалось бы, вовсе нет. Так, обычная индуктивная катушка при достаточно высо­ких частотах представляет собой линию с распределенными парамет­рами (рис. 5.1, б). Из рисунка (рис. 5.1, в) видно, что кроме индуктивностей в схеме замещения есть межвитковые емкости и емкости на корпус прибора (на землю).

Если по катушке проходит переменный ток, то через межвитко­вые емкости и емкости на землю также идет ток. При одном и том же напряжении между соседними витками ток через емкости тем больше, чем выше частота переменного тока. При низкой частоте (десятки, сотни, тысячи герц) ток через емкости несоизмеримо мал, по сравнению с токами через витки катушки, и наличие емкостей можно не учитывать в расчете (что и делалось до сих пор).

Если же частота тока очень велика, например сотни миллиардов герц, то токи через емкости могут во много раз превышать токи через витки катушки. В этом случае вся катушка в целом будет оказывать прохождению переменного тока емкостное, а не индуктивное сопротивление (коли­чественные изменения перешли в качественные).

При промежуточных частотах, порядка нескольких мегагерц (когда линейные размеры ка­тушки соизмеримы с длиной волны), индуктивная катушка является типичной линией с распределенными параметрами.

Если индуктивная катушка намотана на стальной сердечник, который способен насы­щаться, и частота тока достаточно велика, то все устройство в целом представляет собой сложную совокупность из электрической и маг­нитной нелинейных цепей с распределенными параметрами.

В курсе ТОЭ изучают только основы однородных линейных цепей с распределенными параметрами. Вся теория излагается применительно к электрическим линиям с распределенными параметрами на перемен­ном токе. Теория однородных линейных электрических цепей с рас­пределенными параметрами на постоянном токе непосредственно сле­дует из теории цепей переменного тока, если принять угловую частоту равной нулю.

Теория однородных линейных магнитных линий на постоянном токе в значительной мере аналогична теории однородных линейных электрических линий с распределенными параметрами, только вместо тока в уравнении должны быть подставлены:

Источник

Цепи с распределенными параметрами

Вы будете перенаправлены на Автор24

Электрические цепи с распределенными параметрами. Задача анализа цепей с распределенными параметрами.

Цепь с распределенными параметрами – это электрическая цепь, в которой магнитное и электрическое поле, а также потери электрической энергии равномерно или неравномерно распределены вдоль всей цепи.

Процессы в электрических цепях с распределенными параметра могут быть описаны дифференциальными уравнениями в частных производных

Возможность описания цепи с распределенными параметрами обусловлено тем, что длина электромагнитных колебаний в ней равна, а токи и напряжения в такой одномерной цепи представляют собой функции таких переменных, как время и координата х. Изначально, как одномерные линии, использовались двухпроводные линии передачи сигнала от источника к нагрузке, длина которых значительно больше, чем волны передаваемых электромагнитных колебаний. Схема такой линии представлена на рисунке ниже.

Рисунок 1. Двухпроводная линия передачи сигнала от источника к нагрузке. Автор24 — интернет-биржа студенческих работ

Данные цепи также называют длинными линиями, а в том случае, когда диаметр проводов, их взаимное расположение, а также параметры сохраняются во времени, то их называют однородными. Задача анализа электрических цепей с распределенными параметрами заключается в определении характера изменения напряжения и токов вдоль цепи, а также исследование частотных и временных характеристик. Для этого рассматривается электрическая модель участка линии малой длины. Данная модель может быть представлена в виде электрической цепи с сосредоточенными параметрами, которая показана на рисунке ниже.

Готовые работы на аналогичную тему

Рисунок 2. Электрическая цепь с сосредоточенными параметрами. Автор24 — интернет-биржа студенческих работ

Когда электрический ток проходит по проводнику, вокруг него образуется внешнее магнитное поле, модулируемое индуктивностью, которая препятствует прохождению тока. При этом проводник обладает сопротивлением материала (из которого ион зготовлен), поэтому данные элементы соединяются последовательно. Проводники объединяются диэлектриком, обладающим резистивной проводимостью. Между проводниками электрической цепи с распределенными параметрами создается разность потенциалов, из-за чего вокруг проводников создается электрическое поле, которое моделируется емкостью. Таким образом к основным параметрам цепи с распределенными параметрами относятся:

Так как перечисленные параметры имеют конечную длину, то вводится такое понятие, как погонные параметры, рассчитываемые следующим образом:

Примерами электрических цепей с распределенными параметрами, которые применяются промышленности и строительстве являются: коаксиальный кабель, полосковая линия, витая пара, электрический кабель и т.п.

Режимы работы длинной линии

В зависимости от соотношения волнового сопротивления и нагрузки, в длинной линии возможны три режима работы:

Падающая электромагнитная волна – это процесс перемещения электромагнитной волны к приемнику энергии от источника.

Режим бегущих волн возможен при определенном виде нагрузок, к которым относятся: полубесконечная длинная линия, то есть та, в которой нет конца, а следовательно, нет отраженной линии; линия, которая нагружена на сопротивление равное волновому (в этом случае коэффициент отражения равен нулю).

В режиме стоячих волн вся падающая волна отражается от нагрузки. Режим стоячих волн имеет место быть в трех случаях. В первом случае он возможен, если линия разомкнута, а волновое сопротивление равняется нулю или бесконечности. Во втором случай, при котором возможен режим стоячих волн, линия является короткозамкнутой, а волновое сопротивление равно нулю. В третьем случае режим стоячих волн возможен, если линия нагружена на реактивное сопротивление. В данном случае коэффициенты отражения являются комплексными величинами, модули которых равны между собой, то есть:

Данное выражение означает, что амплитуды отраженной и прямой волны в длинной линии одинаковы, однако, на их конце не имеется узла и пучности.

Источник

ФНЧ на элементах с распределенными параметрами

Физические размеры сосредоточенных элементов уменьшаются с повышением частоты и на частотах выше нескольких сотен мегагерц становятся настолько малы­ми, что их изготовление и применение вызывают серьезные трудности. Кроме того, по мере повышения частоты на параметры сосредоточенных элементов все большее влияние начинают оказывать излучение и тепловые потери в них. Поэтому на достаточно высоких частотах предпочтение часто отдается отрезкам линии передачи, используемым в качестве элементов фильтров. Подбором длин и волновых сопротив­лений таких отрезков стараются смоделировать поведение сосредоточенных элемен­тов в схеме соответствующего фильтра-прототипа. Однако такой подход к синтезу фильтров является лишь начальным и весьма грубым приближением, поскольку в этом случае не учитывается ряд важных факторов, влияющих на частотную характе­ристику фильтра, таких, как реактивности в месте стыка отрезков линий передачи, дисперсия в линиях передачи, периодичность частотных характеристик элементов с распределенными параметрами. Поэтому схемы фильтров, полученные подобным методом синтеза, можно рассматривать как первое или начальное приближение при проектировании фильтров.

Чтобы понять, как с помощью отрезка линии передачи можно смоделировать поведение сосредоточенного реактивного элемента (например, индуктивности или емкости), обратимся к рис. 3.8, на котором изображена Т-образная эквивалентная схема отрезка линии передачи и выписаны соответствующие формулы. Когда отрезок линии имеет достаточно малую физическую длину, можно в первом прибли­жении пренебречь тепловыми потерями в нем. В формулах перехода (рис. 3.8, б) гиперболические функции перейдут в тригонометрические, а эквивалентная схема будет содержать лишь реактивные элементы (рис. 3.8, в).

При записи (3.8) и (3.9) полагалось, что α = 0. Если короткий отрезок линии представить П-образной эквивалентной схемой, то, рассуждая аналогично, при α = 0 прихо­дим к следующим равенствам:

Отметим, что в (3.9) и (3.10) не входит функция тангенса, что является положитель­ным моментом, поскольку во многих микро­компьютерах при вычислениях значения аргумента приводятся к первому или третьему квадранту. Поэтому требуется дополнительная проверка, чтобы выяснить принадлежность аргумента ко второму или четвертому квадранту.

Подставляя в (3.8)–(3.11) β=ω/ν_ф и используя аппроксимацию tg θ ≈ sin θ ≈ θ, которая верна при малых длинах отрезка линии, получаем следующие формулы:

для эквивалентной Т-образной схемы:

; (3.12)

; (3.13)

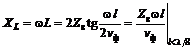
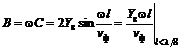
для эквивалентной П-образной схемы:

; (3.14)

. (3.15)

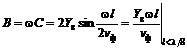
Рис. 3.8. Отрезок линии (а)и его эквива­лентные симметричная Т-образная схема (б)и схема на сосредоточенных элементах при отсутствии потерь (в)

Идентичность формул (3.12) и (3.14), а также (3.13) и (3.15) указывает на дуальность эквивалентных Т- и П-образных схем для отрезка линии передачи.

; (3.16); . (3.17)

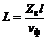
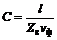
Поэтому, если короткий отрезок линии передачи с весьма высоким волновым сопротивлением включен в разрыв линии с более низким волновым сопротивлением, то в (3.17) С → 0. Следовательно, такой отрезок эквивалентен включенной последова­тельно индуктивности. Соответственно, если в разрыв линии передачи с высоким волновым сопротивлением включитьотрезок с малым волновым сопротивлением, то согласно (3.16) и (3.17) такой отрезок будет вести себя как емкость, включенная в линию параллельно.

Опираясь на рассмотренные элементы с распределенными параметрами, эквива­лентные сосредоточенным, можно реализовать ряд элементов с другим включением: параллельная индуктивность, последовательный контур, включенный параллельно, и др. Эквиваленты схем на сосредоточенных элементах и их реализация на элементах с распределенными параметрами из полосковой (микрополосковой) линии передачи, а также границы применимости приведены в табл. 3.3. Реализация с помощью отрезков полосковых и микрополосковых линий сосредо­точенных элементов типа В, D или Е, но включенных последовательно,возможна лишь с использованием специальных приемов.

Представление цепей на сосредоточенных элементах с помощью элементов с распределенными параметрами

Например, для реализации последова­тельно включенной емкости в отрезке линии прорезаются поперечные щели. Необхо­димость в таких элементах возникает при реализации из отрезков линии передачи сосредоточенных элементов фильтров-прототипов верхних частот и полосовых.

Пример 3.2. Сконструировать ФНЧ с максимально плоской характеристикой и частотой среза 1 ГГц из отрезков однородной линии передачи. Рассмотрение показало, что фильтр должен иметь пять звеньев и его следует встроить в 25-омную линиюпередачи. Фильтр реализуется на полосковой линии с относительной толщиной полоски t/b = 0,05 и относительной диэлектрической проницаемостью заполняющего диэлектрика 4, Рассчитать затухание, вносимое фильтром на частоте 2 ГГц.

1. Рассчитываем g-параметры для пятизвенного фильтра-прототипа с макси­мальной плоской характеристикой:

2. Топологию выбираем так, чтобы ее полосковая реализация была по возможности проще, в частности, следует избегать последовательно включаемых конденсаторов (рис. 3.9).

3. Вычисляем значения L и С в выбранной схеме при условии, что частота среза 1 ГГц или

;

;

;

.

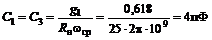
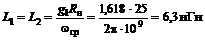
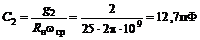
4. Затухание, вносимое фильтром на частоте 2 ГГц, рассчитывается по формуле(3.4):

.

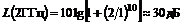
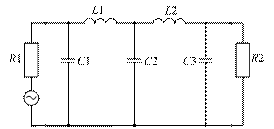Рис. 3.9. Схема фильтра к примеру 3.2

5. Построим схему фильтра на элементах с распределенными параметрами, эквивалентную схеме со сосредоточенными элементами (рис. 3.10).

При проектировании устройств из отрезков линии передачи можно варьировать двумя параметрами: волновым сопротивлением и длиной.

Обычно при создании фильтров волновое сопротивление отрезков с высоким и низким волновыми сопротивлениями, необходимых для реализации эквивалентных сосредоточенных L и C, выбирается исходя из конструктивных особенностей линии, а требуемый размер элемента достигается подбором длины отрезка.

Ограничения на максимальное и минимальное значения волнового сопротивления линии зависят в каждом конкретном случае от используемых материалов. При реализации фильтра на симметричной полосковой линии ε_r = 4 ширина полоски в питающей линии с волновым сопротивлением 25 Ом равна 7 мм. Рассмотрим ограничения, накладываемые на выбор ширины полоски W₂в отрезке линии с низким волновым сопротивлением (рис. 3.10), являющимся распределенным аналогом параллельного конденсатора С₁ в схеме на рис. 3.9. Наибольшая ширина W₂ограничена разме­ром, при котором в линии возникает поперечный резонанс. Поэтому целесообразно выбирать ее не более четверти длины волны на самой высокой рабочей частоте (пусть в данном случае она равна 1,5 см). Это позволяет сохранять одноволновый режим в линии. При W₂ = = 1,5 см волновое сопротивление равно 12,5 Ом. Минимальная ширина полоски W₃ ограничивается принятой технологией и обычно должна быть не менее 1 мм. При W₃= 1 мм волновое сопротивление отрезка равно 70 Ом.

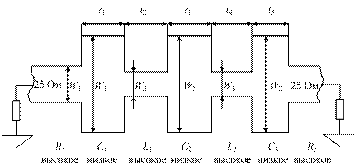Рис. 3.10. Фильтр нижних частот на элементах с распределенными параметрами

Прежде чем продолжать расчет, напомним, что в проводимом приближенном синтезе схемы фильтра не учитывается влияние неоднородностей, возникающих в местах стыка отрезков с разными волновыми сопро­тивлениями. Влияние неоднородностей обсуждается в конце данного раздела.

Длина отрезка линии, реализующего индуктивность L:

где λ_gL и Z_вL – соответственно длина волны и волновое сопротивление для этого отрезка линии. Длина отрезка линии, реализующего емкость С:

где λ_gC и Z_вC – соответственно длина волны и волновое сопротивление для этого отрезка линии.

где .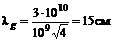

Если при вычислениях значения функции arc sin получаются в градусах, то их следует перевести в радианы.

Теперь рассчитываем длины отрезков, см, соответствующих конденсаторам с параметрами С₁= С₃= 4 пФи С₂= 12,7пФ:

На этом проектирование фильтра в первом приближении заканчивается.

Полученное значение l₃ = 3,6 см довольно велико. Для уменьшения длины отрез­ка l₃ следует снизить его волновое сопротивление. При рассчитанных длинах всех отрезков общая длина конструкции около 8 см, что составляет примерно половину длины волны в линии на частоте 1 ГГц.

В проведенном выше первоначальном расчете не учитывалось влияние концевых емкостей в эквивалентной П-образной схеме отрезка линии с высоким волновым сопротивлением. Реактивное сопротивление этих конденсаторов

или, в случае короткого отрезка линии:

. (3.18)

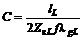
Аналогично пренебрегалось влиянием концевых индуктивностей в эквивалент­ной Т-образной схеме отрезка линии с низким волновым сопротивлением. Значения этих индуктивностей можно определить по формуле

. (3.19)

Для более точного описания реальной физической ситуации эти параметры следует включить в первоначальный расчет. Конструкцию фильтра (см. рис. 3.10) представим в виде эквивалентной схемы, состоящей из сосредоточенных элементов, включив в нее концевые емкости и индуктивнос­ти. Такая эквивалентная схема (рис. 3.11) более точно аппроксимирует конструкцию на рис. 3.10, чем схема фильтра-прототипа (см. рис. 3.9). Схема на рис. 3.11 образуется полными Т- и П-образными эквивалентными схемами для каждого отрезка линии, входящего в конструкцию фильтра.

Следующим шагом, служащим продолжением первоначально выполненного расчета, где пренебрегалось влиянием концевых реактивностей, является вычисле­ние значений концевых элементов по формулам (3.18) и (3.19).

Рис. 3.11. Эквивалентная схема к примеру 3.2, использующая полные Т- и П- образные схемы замещения для каждого отрезка линии

Расчет элементов эквивалентной схемы на рис. 3.11 выполняем следующим обра­зом. Вначале скорректируем полученные ранее значения емкостей, не учитывая концевые индуктивности. Это позволяет при проектировании фильтра учесть влия­ние концевых емкостей для отрезков линии, реализующих индуктивности. Коррек­ция состоит в вычитании рассчитанных значений концевых емкостей из полученных ранее значений емкостей С₁, С₂ и С₃. Новые значения емкостей используются для определения новых длин отрезков, их реализующих. После этого вычисляем значения концевых индуктивностей для отрезков линии с низким волновым сопротивлени­ем. Полученные значения вычитаем из рассчитанных ранее значений L₁и L₂ для фильтра-прототипа. Находим новые длины отрезков, реализующих новые значения индуктивностей.

Описанный выше процесс вычисления концевых индуктивностей и емкостей, которые используются для коррекции параметров ранее рассчитанных элементов фильтра-прототипа и получения уточненных длин отрезков линии, повторяется до тех пор, пока скорректированные значения индуктивностей и емкостей не начнут приближаться к некоторым фиксированным значениям. Таким путем определяются уточненные значения длин отрезков, рассчитанные вначале с помощью фильтра-прототипа на сосредоточенных элементах.

Источник