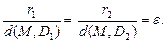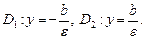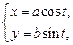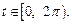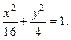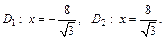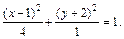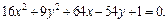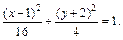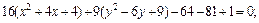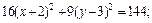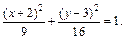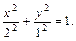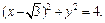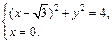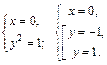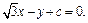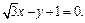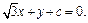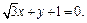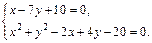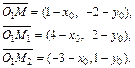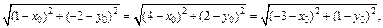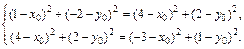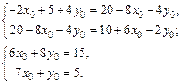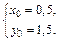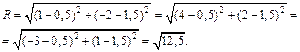эллипс параметры и свойства

Среди центральных кривых второго порядка особое место занимает эллипс, близкий к окружности, обладающий похожими свойствами, но всё же уникальный и неповторимый.

Определение и элементы эллипса

Множество точек координатной плоскости, для каждой из которых выполняется условие: сумма расстояний до двух заданных точек (фокусов) есть величина постоянная, называется эллипсом.

По форме график эллипса представляет замкнутую овальную кривую:

Наиболее простым случаем является расположение линии так, чтобы каждая точка имела симметричную пару относительно начала координат, а координатные оси являлись осями симметрии.

Отрезки осей симметрии, соединяющие две точки эллипса, называются осями. Различаются по размерам (большая и малая), а их половинки, соответственно, считаются полуосями.

Точки эллипса, являющиеся концами осей, называются вершинами.

Расстояния от точки на линии до фокусов получили название фокальных радиусов.

Расстояние между фокусами есть фокальное расстояние.

Отношение фокального расстояния к большей оси называется эксцентриситетом. Это особая характеристика, показывающая вытянутость или сплющенность фигуры.

Основные свойства эллипса

имеются две оси и один центр симметрии;

при равенстве полуосей линия превращается в окружность;

все точки фигуры лежат внутри прямоугольника со сторонами, равными большой и малой осям эллипса, проходящими через вершины параллельно осям.

Уравнение эллипса

Пусть линия расположена так, чтобы центр симметрии совпадал с началом координат, а оси – с осями координат.

Для составления уравнения достаточно воспользоваться определением, введя обозначение:

а – большая полуось (в наиболее простом виде её располагают вдоль оси Оx) (большая ось, соответственно, равна 2a);

c – половина фокального расстояния;

M(x;y) – произвольная точка линии.

В этом случае фокусы находятся в точках F₁(-c;0); F₂(c;0)

После ввода ещё одного обозначения

получается наиболее простой вид уравнения:

Параметр b численно равен полуоси, расположенной вдоль Oy (a > b).

В случае (b b) формула эксцентриситета (ε) принимает вид:

Чем меньше эксцентриситет, тем более сжатым будет эллипс.

Площадь эллипса

Площадь фигуры (овала), ограниченной эллипсом, можно вычислить по формуле:

a – большая полуось, b – малая.

Площадь сегмента эллипса

Часть эллипса, отсекаемая прямой, называется его сегментом.

Длина дуги эллипса

Длина дуги находится с помощью определённого интеграла по соответствующей формуле при введении параметра:

Радиус круга, вписанного в эллипс

В отличие от многоугольников, круг, вписанный в эллипс, касается его только в двух точках. Поэтому наименьшее расстояние между точками эллипса (содержащее центр) совпадает с диаметром круга:

Радиус круга, описанного вокруг эллипса

Окружность, описанная около эллипса, касается его также только в двух точках. Поэтому наибольшее расстояние между точками эллипса совпадает с диаметром круга:

Онлайн калькулятор позволяет по известным параметрам вычислить остальные, найти площадь эллипса или его части, длину дуги всей фигуры или заключённой между двумя заданными точками.

Как построить эллипс

Построение линии удобно выполнять в декартовых координатах в каноническом виде.

Строится прямоугольник. Для этого проводятся прямые:

Сглаживая углы, проводится линия по сторонам прямоугольника.

Полученная фигура есть эллипс. По координатам отмечается каждый фокус.

При вращении вокруг любой из осей координат образуется поверхность, которая называется эллипсоид.

Источник

Эллипс и его свойства

причём

Также эллипс можно определить как:

Содержание

Связанные определения

Соотношения между элементами фигуры

.

— большая полуось
— малая полуось
— фокальное расстояние
— фокальный параметр
— перифокусное расстояние
— апофокусное расстояние

Координатное представление

Длина дуги эллипса

Длина дуги плоской линии определяется по формуле:

Воспользовавшись параметрическим представлением эллипса получаем следующее выражение:

После замены выражение для длины дуги принимает окончательный вид:

,

Приближённые формулы для периметра

Максимальная погрешность этой формулы

0,63 % при эксцентриситете эллипса

0,988 (соотношение осей

1/6,5). Погрешность всегда положительная.

Приблизительно в два раза меньшие погрешности в широком диапазоне эксцентриситетов дает формула:

, где

Максимальная погрешность этой формулы

0,36 % при эксцентриситете эллипса

0,980 (соотношение осей

1/5). Погрешность также всегда положительная.

Существенно лучшую точность при Рамануджана :

При эксцентриситете эллипса

0,980 (соотношение осей

1/5) погрешность составляет

0,02 %. Погрешность всегда отрицательная.

Еще точней оказалась вторая формула Рамануджана:

Точные формулы для периметра

Джеймс Айвори и Фридрих Бессель независимо друг от друга получили формулу для периметра эллипса:

где — Арифметико-геометрическое среднее 1 и , а — модифицированное арифметико-геометрическое среднее 1 и , которое было введено С. Ф. Адлаем в статье 2012 года.

Площадь эллипса

Площадь эллипса вычисляется по формуле

Шаблон:Нет АИ

Если эллипс задан уравнением , то площадь можно определить по формуле

.

Источник

Эллипс параметры и свойства

Рассмотрим свойства эллипса.

Эллипс пересекает каждую из осей координат в двух точках.

Пусть – произвольная точка эллипса. Найдем расстояния от точки до фокусов эллипса.

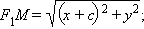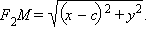Рассмотрим выражение

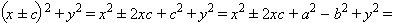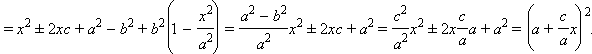Здесь мы учли, что координаты точки удовлетворяют уравнению эллипса.

Сумма расстояний от любой точки эллипса до его фокусов есть величина постоянная и равная удвоенной большей полуоси.

Действительно, используя полученные выражения для расстояний от точки эллипса до его фокусов, получим

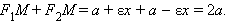Эллипс имеет две взаимно перпендикулярные оси симметрии.

В качестве характеристики формы эллипса удобнее пользоваться эксцентриситетом. Так как

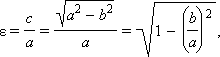то чем больше ε, тем более сжат эллипс.

При малых значениях эксцентриситета эллипс мало отличается от окружности. При эллипс превращается в окружность.

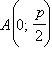
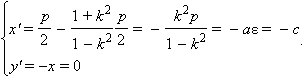Координаты точки при переходе в новую систему будут равны:

То есть точка в новой системе координат имеет те же координаты, что и фокус 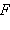эллипса и поэтому совпадет с ним.

С учетом свойств симметрии эллипса, свойство, с помощью которого мы определили эллипс, в новых терминах можно сформулировать следующим образом: отношение расстояния от любой точки эллипса до одного из его фокусов к расстоянию от этой точки до соответствующей ему директрисы есть величина постоянная и равная эксцентриситету. Вид эллипса в канонической системе координат и его директрисы приведены на рис. 10.8.1.

Источник

Эллипс — свойства, уравнение и построение фигуры

Среди центральных кривых второго порядка особое место занимает эллипс, близкий к окружности, обладающий похожими свойствами, но всё же уникальный и неповторимый.

Определение и элементы эллипса

Множество точек координатной плоскости, для каждой из которых выполняется условие: сумма расстояний до двух заданных точек (фокусов) есть величина постоянная, называется эллипсом.

По форме график эллипса представляет замкнутую овальную кривую:

Наиболее простым случаем является расположение линии так, чтобы каждая точка имела симметричную пару относительно начала координат, а координатные оси являлись осями симметрии.

Отрезки осей симметрии, соединяющие две точки эллипса, называются осями. Различаются по размерам (большая и малая), а их половинки, соответственно, считаются полуосями.

Точки эллипса, являющиеся концами осей, называются вершинами.

Расстояния от точки на линии до фокусов получили название фокальных радиусов.

Расстояние между фокусами есть фокальное расстояние.

Отношение фокального расстояния к большей оси называется эксцентриситетом. Это особая характеристика, показывающая вытянутость или сплющенность фигуры.

Основные свойства эллипса

имеются две оси и один центр симметрии;

при равенстве полуосей линия превращается в окружность;

все точки фигуры лежат внутри прямоугольника со сторонами, равными большой и малой осям эллипса, проходящими через вершины параллельно осям.

Уравнение эллипса

Пусть линия расположена так, чтобы центр симметрии совпадал с началом координат, а оси – с осями координат.

Для составления уравнения достаточно воспользоваться определением, введя обозначение:

а – большая полуось (в наиболее простом виде её располагают вдоль оси Оx) (большая ось, соответственно, равна 2a);

c – половина фокального расстояния;

M(x;y) – произвольная точка линии.

В этом случае фокусы находятся в точках F1(-c;0); F2(c;0)

После ввода ещё одного обозначения

получается наиболее простой вид уравнения:

a 2 b 2 — a 2 y 2 — x 2 b 2 = 0,

Параметр b численно равен полуоси, расположенной вдоль Oy (a > b).

В случае (b b) формула эксцентриситета (ε) принимает вид:

Чем меньше эксцентриситет, тем более сжатым будет эллипс.

Площадь эллипса

Площадь фигуры (овала), ограниченной эллипсом, можно вычислить по формуле:

a – большая полуось, b – малая.

Площадь сегмента эллипса

Часть эллипса, отсекаемая прямой, называется его сегментом.

, где

(xo;y0) – крайняя точка сегмента.

Длина дуги эллипса

Длина дуги находится с помощью определённого интеграла по соответствующей формуле при введении параметра:

Радиус круга, вписанного в эллипс

В отличие от многоугольников, круг, вписанный в эллипс, касается его только в двух точках. Поэтому наименьшее расстояние между точками эллипса (содержащее центр) совпадает с диаметром круга:

Радиус круга, описанного вокруг эллипса

Окружность, описанная около эллипса, касается его также только в двух точках. Поэтому наибольшее расстояние между точками эллипса совпадает с диаметром круга:

Онлайн калькулятор позволяет по известным параметрам вычислить остальные, найти площадь эллипса или его части, длину дуги всей фигуры или заключённой между двумя заданными точками.

Как построить эллипс

Построение линии удобно выполнять в декартовых координатах в каноническом виде.

Строится прямоугольник. Для этого проводятся прямые:

Сглаживая углы, проводится линия по сторонам прямоугольника.

Полученная фигура есть эллипс. По координатам отмечается каждый фокус.

При вращении вокруг любой из осей координат образуется поверхность, которая называется эллипсоид.

Источник

Параметры эллипса

Точки F₁(–c, 0) и F₂(c, 0), где 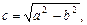называются фокусами эллипса, при этом величина 2c определяет междуфокусное расстояние.

Точки А₁(–а, 0), А₂(а, 0), В₁(0, –b), B₂(0, b) называются вершинами эллипса (рис. 9.2), при этом А₁А₂ = 2а образует большую ось эллипса, а В₁В₂ – малую, 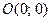– центр эллипса.

Основные параметры эллипса, характеризующие его форму:

ε = с/a – эксцентриситет эллипса;

– фокальные радиусы эллипса (точка М принадлежит эллипсу), причем r₁ = a + εx, r₂ = a – εx;

– директрисы эллипса.

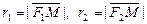
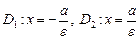
Для эллипса справедливо: 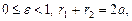директрисы не пересекают границу и внутреннюю область эллипса, а также обладают свойством

Эксцентриситет эллипса выражает его меру «сжатости».

Если b > a > 0, то эллипс задается уравнением (9.7), для которого вместо условия (9.8) выполняется условие

. (9.9)

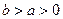
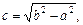
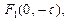
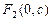
Тогда 2а – малая ось, 2b – большая ось, – фокусы (рис. 9.3). При этом r₁ + r₂ = 2b,
ε = c/b, директрисы определяются уравнениями:

При условии 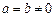имеем (в виде частного случая эллипса) окружность радиуса R = a. При этом с = 0, а значит, ε = 0.

Точки эллипса обладают характеристическим свойством: сумма расстояний от каждой из них до фокусов есть величина постоянная, равная 2а (рис. 9.2).

Для параметрического задания эллипса (формула (9.7)) в случаях выполнения условий (9.8) и (9.9) в качестве параметра t может быть взята величина угла между радиус-вектором точки, лежащей на эллипсе, и положительным направлением оси Ox:

где

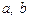
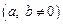
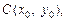
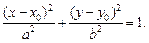
Если центр эллипса с полуосями находится в точке то его уравнение имеет вид:

(9.10)

Пример 1. Привести уравнение эллипса x 2 + 4y 2 = 16 к каноническому виду и определить его параметры. Изобразить эллипс.

Решение. Разделим уравнение x 2 + 4y 2 = 16 на 16, после чего получим:

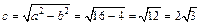
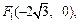
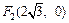
По виду полученного уравнения заключаем, что это каноническое уравнение эллипса (формула (9.7)), где а = 4 – большая полуось, b = 2 – малая полуось. Значит, вершинами эллипса являются точки A₁(–4, 0), A₂(4, 0), B₁(0, –2), B₂(0, 2). Так как – половина междуфокусного расстояния, то точки являются фокусами эллипса. Вычислим эксцентриситет:

Изображаем эллипс (рис. 9.4).

Пример 2. Определить параметры эллипса

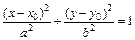
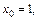
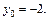
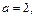
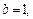
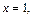
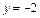
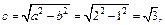
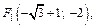
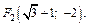
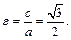
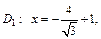
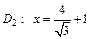
Решение. Сравним данное уравнение с каноническим уравнением эллипса со смещенным центром. Находим центр эллипса С: Большая полуось малая полуось прямые – главные оси. Половина междуфокусного расстояния а значит, фокусы Эксцентриситет Директрисы D₁ и D₂ могут быть описаны с помощью уравнений: (рис. 9.5).

Пример 3. Определить, какая кривая задается уравнением, изобразить ее:

3) x 2 + 4y 2 – 2x + 16y + 1 = 0; 4) x 2 + 4y 2 – 2x + 16y + 17 = 0;

5)

Решение. 1) Приведем уравнение к каноническому виду методом выделения полного квадрата двучлена:

(x 2 + 4x + 4) – 4 + (y 2 – 2y + 1) – 1 + 4 = 0;

Таким образом, уравнение может быть приведено к виду

Это уравнение окружности с центром в точке (–2, 1) и радиусом R = 1 (рис. 9.6).

2) Выделяем полные квадраты двучленов в левой части уравнения и получаем:

Это уравнение не имеет смысла на множестве действительных чисел, так как левая часть неотрицательна при любых действительных значениях переменных x и y, а правая – отрицательна. Поэтому говорят, что это уравнение «мнимой окружности» или оно задает пустое множество точек плоскости.

3) Выделяем полные квадраты:

(x 2 – 2x + 1) – 1 + 4(y 2 + 4y + 4) – 16 + 1 = 0;

(x – 1) 2 + 4(y + 2) 2 – 16 = 0;

Значит, уравнение имеет вид:

или

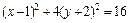
Полученное уравнение, а следовательно, и исходное задают эллипс. Центр эллипса находится в точке О₁(1, –2), главные оси задаются уравнениями y = –2, x = 1, причем большая полуось а = 4, малая полуось b = 2 (рис. 9.7).

4) После выделения полных квадратов имеем:

(x – 1) 2 + 4(y + 2) 2 – 17 + 17 = 0 или (x – 1) 2 + 4(y + 2) 2 = 0.

Полученное уравнение задает единственную точку плоскости с координатами (1, –2).

5) Приведем уравнение к каноническому виду:

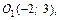
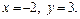
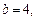
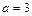
Очевидно, оно задает эллипс, центр которого находится в точке главные оси задаются уравнениями причем большая полуось малая полуось (рис. 9.8).

Пример 4. Записать уравнение касательной к окружности радиуса 2 с центром в правом фокусе эллипса x 2 + 4y 2 = 4 в точке пересечения с осью ординат.

Решение. Уравнение эллипса приведем к каноническому виду (9.7):

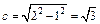
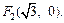
Значит, и правый фокус – Поэтому, искомое уравнение окружности радиуса 2 имеет вид (рис. 9.9):

Окружность пересекает ось ординат в точках, координаты которых определяются из системы уравнений:

Пусть это точки N (0; –1) и М (0; 1). Значит, можно построить две касательные, обозначим их Т₁ и Т₂. По известному свойству касательная перпендикулярна радиусу, проведенному в точку касания.

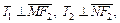
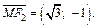
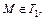
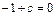
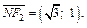
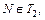
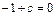
Пусть Тогда уравнение касательной Т₁ примет вид:

значит, или Т₁:

Тогда уравнение касательной Т₂ примет вид:

значит, или Т₂:

Пример 5. Записать уравнение окружности, проходящей через точку М(1, –2) и точки пересечения прямой x – 7y + 10 = 0 с окружностью x 2 + y 2 – 2x + 4y – 20 = 0.

Решение. Найдем точки пересечения прямой x – 7y + 10 = 0 с окружностью x 2 + y 2 – 2x + 4y – 20 = 0, решив систему уравнений:

Выразим х из первого уравнения системы:

Затем подставим во второе:

(7y – 10) 2 + y 2 – 2(7y – 10) + 4y – 20 = 0.

Оно равносильно уравнению

Используя формулы корней квадратного уравнения, найдем y₁ = 1, y₂ = 2, откуда x₁ = –3, x₂ = 4.

Итак, имеем три точки, лежащие на окружности: M(1, –2), M₁(4, 2) и M₂(–3, 1). Пусть О₁(x₀, y₀) – центр окружности. Тогда 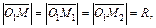где R – радиус окружности.

Найдем координаты векторов:

что равносильно системе

Решая последнюю систему, получаем ответ:

Таким образом, центр окружности находится в точке (0,5; 1,5), ее радиус

Тогда каноническое уравнение искомой окружности имеет вид:

Дата добавления: 2015-09-29 ; просмотров: 5530 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник