фокальный параметр гиперболы формула

Гипербола и её свойства

Гипербола и её форма.

Гиперболой мы назвали линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
\frac>>-\frac>>=1.\label
$$

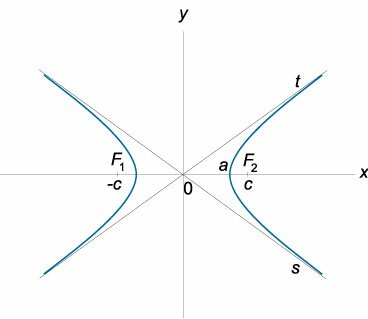
Из этого уравнения видно, что для всех точек гиперболы \(|x| \geq a\), то есть все точки гиперболы лежат вне вертикальной полосы ширины \(2a\) (рис. 8.6). Ось абсцисс канонической системы координат пересекает гиперболу в точках с координатами \((a, 0)\) и \((-a, 0)\), называемых вершинами гиперболы. Ось ординат не пересекает гиперболу. Таким образом, гипербола состоит из двух не связанных между собой частей. Они называются ее ветвями. Числа \(a\) и \(b\) называются соответственно вещественной и мнимой полуосями гиперболы.

Рис. 8.6. Гипербола.

Для гиперболы оси канонической системы координат являются осями симметрии, а начало канонической системы — центром симметрии.

Доказательство аналогично доказательству соответствующего утверждения для эллипса.

Рис. 8.7. Пересечение прямой и гиперболы.

Числитель дроби \(ab/v\) постоянен, а знаменатель принимает наибольшее значение при \(k=0\). Следовательно, наименьшую абсциссу имеет вершина \((a, 0)\). С ростом \(k\) знаменатель убывает, и \(x\) растет, стремясь к бесконечности, когда \(k\) приближается к числу \(b/a\). Прямая \(y=bx/a\) с угловым коэффициентом \(b/a\) не пересекает гиперболу, и прямые с большими угловыми коэффициентами ее тем более не пересекают. Любая прямая с меньшим положительным угловым коэффициентом пересекает гиперболу.

Если мы будем поворачивать прямую от горизонтального положения по часовой стрелке, то \(k\) будет убывать, \(k^<2>\) расти, и прямая будет пересекать гиперболу во все удаляющихся точках, пока не займет положения с угловым коэффициентом \(-b/a\).

К прямой \(y=-bx/a\) относится все, что было сказано о \(y=bx/a\): она не пересекает гиперболу и отделяет прямые, пересекающие ее, от не пересекающих. Из приведенных рассуждений вытекает, что гипербола имеет вид, изображенный на рис. 8.7.

Прямые с уравнениями \(y=bx/a\) и \(y=-bx/a\) в канонической системе координат называются асимптотами гиперболы.

Источник

Фокальный параметр гиперболы формула

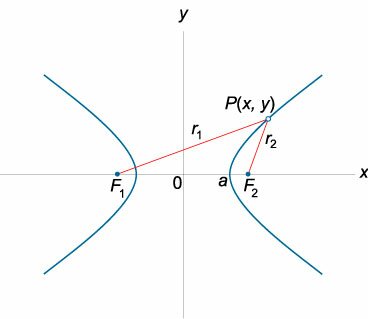
Модуль разности расстояний от любой точки гиперболы до ее фокусов является постоянной величиной:
\(\left| <— > \right| = 2a\),
где \(\), \(\) − расстояния от произвольной точки \(P\left( \right)\) гиперболы до фокусов \(\) и \(\), \(a\) − действительная полуось гиперболы.

Уравнения асимптот гиперболы
\(y = \pm \large\frac\normalsize x\)

Соотношение между полуосями гиперболы и фокусным расстоянием
\( = + \),
где \(c\) − половина фокусного расстояния, \(a\) − действительная полуось гиперболы, \(b\) − мнимая полуось.

Уравнение правой ветви гиперболы в параметрической форме
\( \left\ < \beginx &= a \cosh t \\ y &= b \sinh t \end \right., \;\;0 \le t \le 2\pi\),
где \(a\), \(b\) − полуоси гиперболы, \(t\) − параметр.

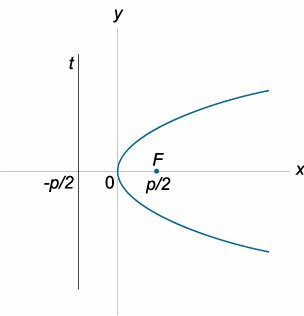
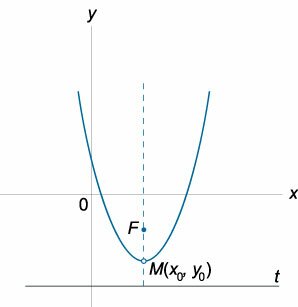
Координаты фокуса
\(F \left( <\large\frac

<2>\normalsize, 0> \right)\)

Координаты вершины
\(M \left( <0,0>\right)\)

Уравнение параболы, ось симметрии которой параллельна оси \(Oy\)
\(A + Dx + Ey + F = 0\;\left( \right) \),
или в эквивалентной форме
\(y = a + bx + c,\;\;p = \large\frac<1><2a>\normalsize\)

Уравнение директрисы
\(y = — \large\frac

<2>\normalsize\),
где \(p\) − параметр параболы.

Координаты фокуса
\(F\left( <, + \large\frac

<2>\normalsize> \right)\)

Уравнение параболы с вершиной в начале координат и осью симметрии, параллельной оси \(Oy\)
\(y = a,\;\;p = \large\frac<1><<2a>>\normalsize\)

Координаты вершины
\(M \left( <0,0>\right)\)

Источник

Фокальный параметр гиперболы формула

По сути, мы получили уравнение эллипса. Упростим его с помощью ряда несложных математических преобразований:

Установим форму эллипса, пользуясь его каноническим уравнением.

2. Найдем точки пересечения эллипса с осями координат. Положив y = 0, найдем точки A ₁ ( a ; 0) и A ₂ (– a ; 0), в которых ось 0 x пересекает эллипс. Положив в уравнении (2.17) x = 0, находим точки пересечения эллипса с осью 0 y : B ₁ (0; b ) и B ₂ (0;– b ). Точки A ₁ , A ₂ , B ₁ , B ₂ называются вершинами эллипса. Отрезки А₁А₂, В₁В₂, а также их длины 2 a и 2 b – соответственно большая и малая оси эллипса (рис. 2.4).

3. Из уравнения (2.17) следует, что каждое слагаемое в левой части не превосходит единицы, т.е.:

4. В уравнении (2.17) левая часть – сумма неотрицательных слагаемых, т.е. при возрастании одного слагаемого другое будет уменьшаться, если | x | возрастает, | y | уменьшается и наоборот.

Отсюда видно, что чем меньше эксцентриситет эллипса, тем будет менее эллипс сплющенным; при ε = 0 эллипс превращается в окружность.

Прямые – директрисы эллипса.

По формуле расстояния между двумя точками получаем:

Эксцентриситет эллипса

Примечание. Если эллипс (окружность) вращать вокруг одной из его осей, то описываемая им поверхность будет эллипсоидом вращения (сферой)

Пример 2.6. В геодезии используется система географических координат, основанная на понятии геоида. Геоид – поверхность Земли, ограниченная уровенной поверхностью, продолженной под континенты. Поверхность геоида отличается от физической поверхности Земли, на которой резко выражены горы и океанические впадины.

Тело, поверхность которого более всего соответствует поверхности геоида, имеет определенные размеры и ориентирована соответственно в теле Земли, называется референц–эллипсоидом. В нашей стране с 1946 года для всех геодезических работ принят референц–эллипсоид Красовского с параметрами a = 6 378 245 м, b = 6 356 863 м, α = 1: 298,3.

Линия, проходящая вертикально через центр эллипсоида является полярной осью. Линия, проходящая через центр эллипсоида, перпендикулярно к полярной оси, – экваториальной осью. При пересечении поверхности эллипсоида плоскостью, проходящей через его центр, перпендикулярно к полярной оси, образуется окружность, называемая экватором. Окружность, полученная от пересечения поверхности эллипсоида плоскостью, параллельной плоскости экватора, называется параллелью. Линия пересечения поверхности эллипсоида с плоскостью, проходящей через заданную точку и полярную ось, называется меридианом данной точки. Положение точки на земной поверхности определяется пересечением параллели и меридиана, проходящих через нее. Угол φ между плоскостью экватора и отвесной линией называется географической широтой. Для определения долгот точек один из меридианов (Гринвичский) принимают за начальный или нулевой. Угол λ, составленный плоскостью меридиана, проходящего через данную точку, и плоскостью начального меридиана, называется географической долготой

Установим форму гиперболы, исходя из ее канонического уравнения.

Примечание. При вращении гиперболы вокруг ее действительной оси образуется двуполостный гиперболоид, вокруг ее мнимой оси – однополостный гиперболоид

Подробно данные уравнения рассмотрены в теме: «Исследование общего уравнения 2–ой степени» (смотри схему 10), частными случаями которого являются данные формулы.

Источник

Гипербола определение, свойства и виды, каноническое уравнение, формула нахождения фокуса, алгоритмы и примеры построения графика функции

При упоминании термина «гипербола» человек с поэтическим складом мышления подумает о преувеличенном сопоставлении. В крайности доходящем до абсурда.

Близкий к математике представит нечто подобное:

Это родственные кривые, полученные при сечении конуса плоскостью. Парабола, эллипс (окружность), гипербола.

Что такое гипербола в математике

Это геометрическое место точек M, физическая разница расстояний от которых до выбранных (F1, F2), называемых фокусами, постоянна.

Оговоримся, что все сказанное относится к Евклидовой плоскости, где параллельные прямые не пересекаются.

Но если из отрезка |F1F2| соорудить координатную прямую X, за начальную точку взять середину (она же будет центром гиперболы) отрезка, то получим декартову систему координат. Где кривая описывается алгебраическим уравнением II-го порядка.

Получим классическую формулу аналитической геометрии:

где a – действительная полуось, b – мнимая.

поскольку x и y связаны квадратной зависимостью, обе оси будут осями симметрии;

пересечения с осью абсцисс (фокусов) с координатами ±a называются вершинами гиперболы, и расстояние между ними является минимальной дистанцией между ветвями (о последних ниже);

кратчайший отрезок от фокуса до вершины зовется перицентрическим расстоянием и пишется «rp».

Асимптоты и фокусы гиперболы

Фокусы находятся на оси X (из этого исходили). Расстояние до центра гиперболы (он же центр симметрии C) называется фокальным и обозначается «c». Его формула:

Умозрительно очевидно, что сечение конуса состоит из двух кривых. Называются они ветвями гиперболы. Также не подлежит сомнению то, что ветви ограничены воображаемой поверхностью. Фокусы всегда находятся внутри ветвей.

Помучившись с производными и пределами, получим формулы асимптот (прямые, расстояние до которых от кривой стремится к нулю на бесконечном удалении от «0»):

Дистанцию от фокуса до асимптоты зовут прицельным параметром и обозначают буквой «b».

Как построить график функции гиперболы

Существует много ресурсов, где можно онлайн наблюдать, как строится функция. Но нужно все уметь самому. Итак, давайте учиться.

Построим для примера график уравнения

По формуле выше выстраиваем асимптоты.

Отмечаем вершины х = ±2 (А1, А2). Приблизительный вид уже ясен.

При х = ±3, y = ±3,5 (примерно).

Эксцентриситет гиперболы

Эксцентриситетом считают величину:

Является параметром, характеризующим отклонение конического сечения от окружности:

кривые с равным эксцентриситетом подобны;

показатель угла наклона асимптот.

Равнобочная (равносторонняя) гипербола

Таковой кривая является при условии a = b. Если покрутить систему координат, функцию можно свести к виду:

Эксцентриситет данной конструкции составит квадратный корень из 2.

Иначе говоря, получаем график обратной пропорциональности:

Или «любимую» школьниками.

Коль уж речь зашла о школьном курсе, добавим сведений:

прямые x = 0, y = 0 – асимптоты;

область определения – все действительные числа, кроме 0;

область значений – все, за исключением 0;

функция нечетная, поскольку меняет знак при смене знака аргумента;

убывающая при положительных и отрицательных x.

Касательная и нормаль

В каждой точке гладкой кривой возможно построить касательную и нормаль (перпендикуляр). Гипербола – не исключение. Касательная – прямая, совпадающая с кривой только в одной точке (в пределах изгиба одного порядка).

Уравнение касательной в точке с координатами (x0y0) имеет вид:

Сопряженные гиперболы

Записанное таким образом уравнение даст сопряженную фигуру:

То есть с теми же асимптотами, но расположенную по-другому, с поворотом на 90°.

Свойства гиперболы

Их должен знать каждый школьник:

Касательная в произвольной точке H окажется биссектрисой угла F1HF2.

Кривая симметрична относительно осей и своего центра.

Отсеченный асимптотами отрезок касательной делится точкой соприкосновения пополам. Площадь же выделенного треугольника не меняется от изменения точки.

Использование

Где применяются знания о гиперболе:

для создания эллиптических и других координат;

в солнечных часах (сечение конуса света);

для анализа движения космических объектов.

Заключение

Непростая кривая с неожиданными в некоторых случаях применением. Что удивительно, задача о сечениях конуса была поставлена древнегреческими учеными во II-м веке до нашей эры. Это говорит о высочайшем уровне тогдашних инженеров.

Нет, солнечные часы понятно были, а мелких искусственных спутников не было точно. И астероиды не исследовали, но вопросы возникали. И были ответы без ссылок на многочисленных богов. Удивительные люди.

Источник

Гипербола

Определение. Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний от каждой из которых до двух данных точек F₁ и F₂, называемых фокусами гиперболы, есть величина постоянная, равная 2а, а>0, меньшая чем расстояние между фокусами.

Выберем декартову прямо-угольную систему координат ОХY так, как показано на рисунке. Тогда F₁F₂=2с, F₁(—с,0), F₂(c,0).

(3)

По свойствам уравнения (3) исследуем свойства гиперболы:

1. Координатные оси являются осями симметрии гиперболы. Поэтому гиперболу достаточно исследовать только в первой координатной четверти.

2. Если у = 0, то x = а. Если х = 0, то уравнение (3) решений не имеет. Значит, гипербола пересекает только ось ОХ в точках А₁(—а,0), А₂(а,0), называемых вершинами гиперболы.

,

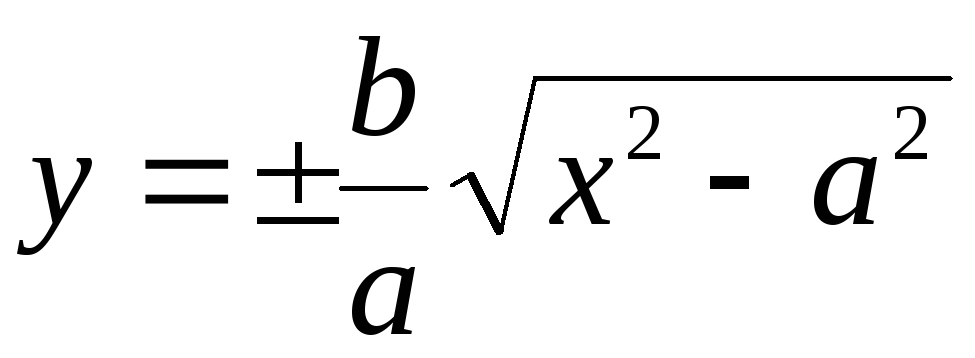
то |х|а. Поэтому гипербола расположена вне полосы, ограниченной прямыми x=а.

4. Если x возрастает от а до +, то из (1.12) следует, что у возрастает от 0 до + в первой координатной четверти.

— наклонные асимптоты гиперболы.

По полученным свойствам строим гиперболу. Отрезок А₁А₂ и его длина 2а называются действительной осью гиперболы, а отрезок ОА₁ и его длина а — действительной полуосью. Отрезок В₁В₂ и его длина 2b — мнимая ось гиперболы, а отрезок ОВ₁ и его длина b— мнимая полуось. Длина отрезка F₁F₂=2с называется фокусным расстоянием, начало координат — центр гиперболы.

Определение. Эксцентриситетом гиперболы называется величина

.

Так как для гиперболы с > а, и следовательно, чем меньше ε, тем более сжата гипербола к оси ОХ.

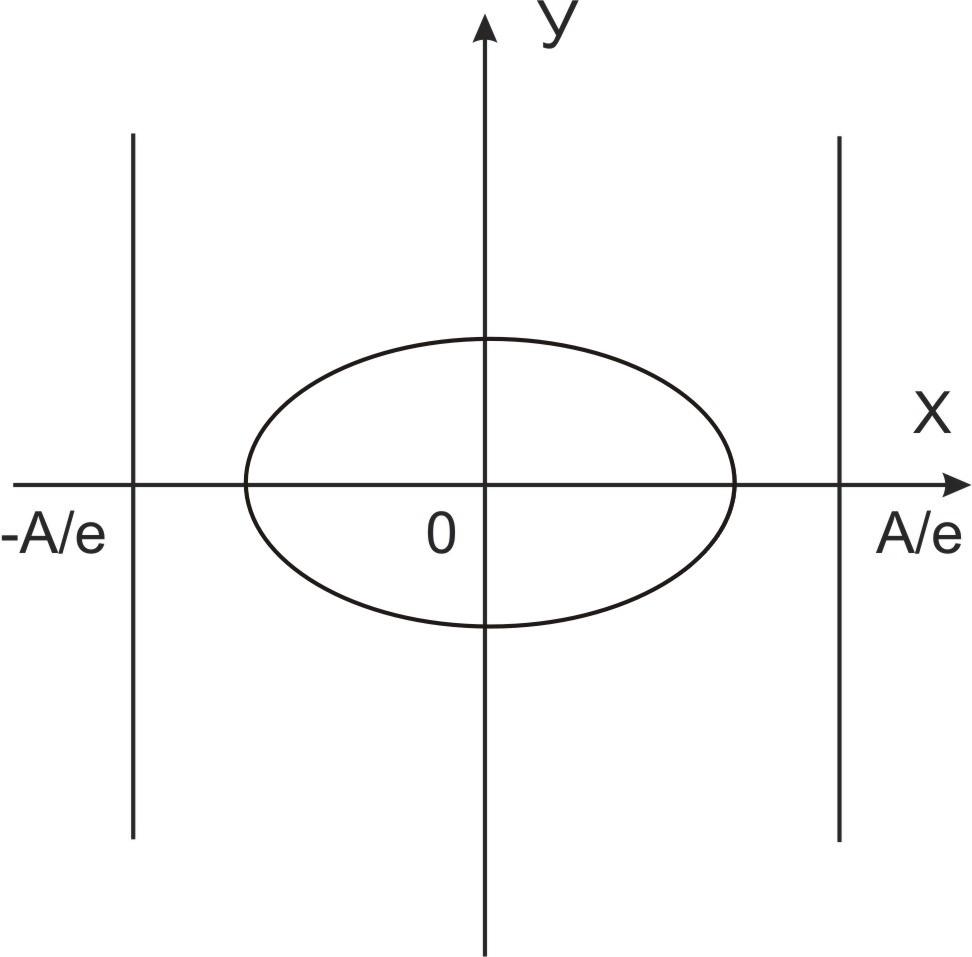
Директрисы эллипса и гиперболы.

Определение. Прямые х=(а/ε), где ε — эксцентриситет эллипса (гиперболы) называются директрисами эллипса (гиперболы).

Теорема. Отношение расстояния от любой точки эллипса (гиперболы) до фокуса к расстоянию до соответствующей директрисы есть величина постоянная, равная эксцентриситету эллипса (гиперболы).

Доказательство, например для эллипса, следует из того, что

M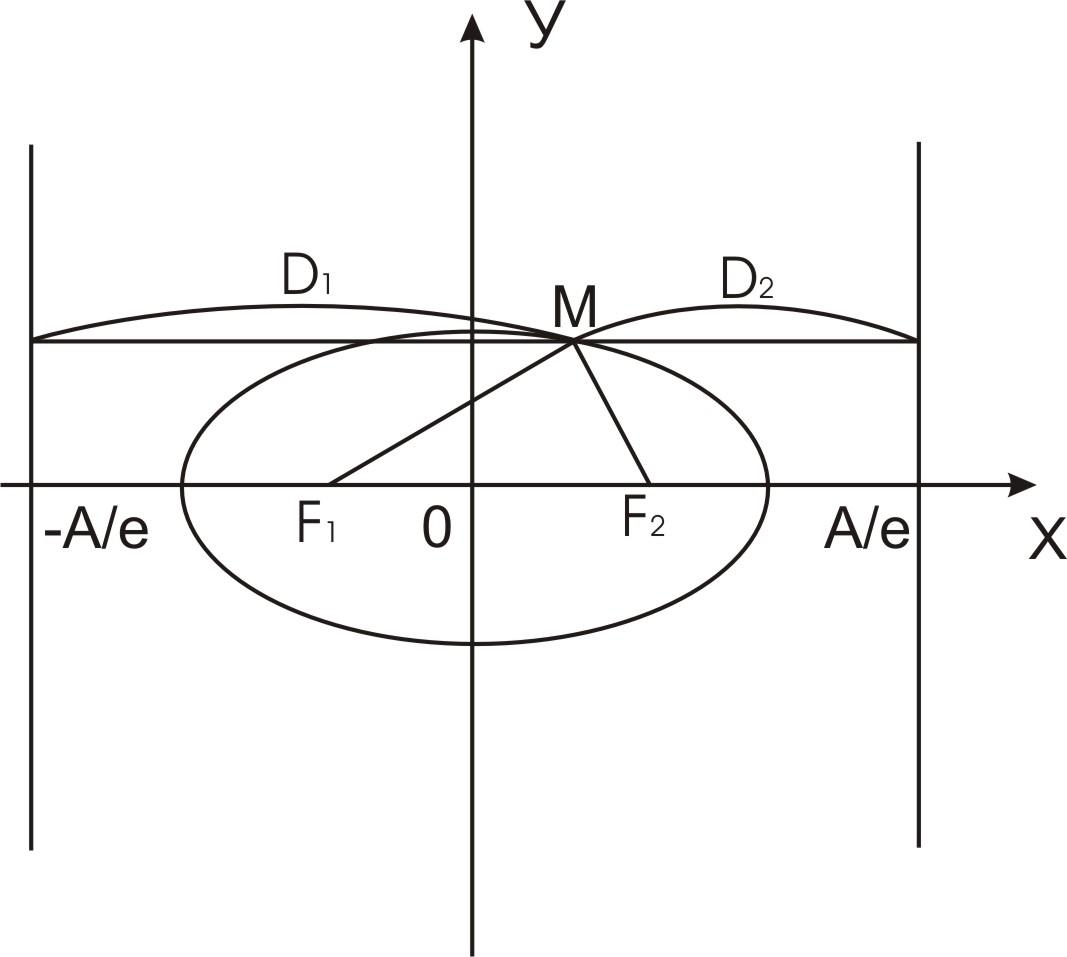F₁=а+εх, МF₂=а—εх.

Заметим, что, так как все точки параболы равноудалены от директрисы и фокуса, то отношение этих расстояний равно 1. Поэтому можно говорить об эксцентриситете параболы и считать его равным 1. Как уже отмечалось, эксцентриситет окружности равен нулю.

Фокальный параметр эллипса и гиперболы

Пусть эллипс и гипербола заданы соответственно своими каноническими уравнениями. Проведем через один из фокусов этих кривых прямую перпендикулярную оси ОХ и обозначим точки ее пересечения с кривой через Р и Р’.

Обозначим длину отрезка РР’ через 2р. Тогда величина р(р>0) называется фокальным параметром эллипса (гиперболы) и равна: .

Если обозначить через d – расстояние между фокусом и директрисой, то .

Так как для параболы ε = 1 и d = р, то делаем следующий Вывод: для эллипса (кроме окружности), гиперболы, парабол фокальный параметр р равен:

где c – эксцентриситет, d – расстояние от фокуса до соответствующей директрисы.

Заметим, что для окружности фокальный параметр равен ее радиусу.

Источник