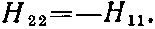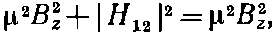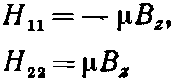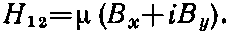гамильтониан частицы в электромагнитном поле

СОДЕРЖАНИЕ

Вступление

Гамильтониан Шредингера

Одна частица

По аналогии с классической механикой гамильтониан обычно выражается как сумма операторов, соответствующих кинетической и потенциальной энергии системы, в виде

Можно также сделать замены в определенных переменных, чтобы соответствовать конкретным случаям, например, некоторым случаям, связанным с электромагнитными полями.

Множество частиц

ЧАС ^ знак равно ∑ п знак равно 1 N Т ^ п + V ^ <\ displaystyle <\ hat > = \ sum _ ^ <\ hat> _ + <\ hat >>

— функция потенциальной энергии, теперь функция пространственной конфигурации системы и времени (конкретный набор пространственных положений в некоторый момент времени определяет конфигурацию) и

Для невзаимодействующих частиц, то есть частиц, которые не взаимодействуют друг с другом и движутся независимо, потенциал системы представляет собой сумму отдельной потенциальной энергии для каждой частицы, т. Е.

Общий вид гамильтониана в этом случае:

Уравнение Шредингера

Формализм Дирака

С математически строгой точки зрения, следует соблюдать осторожность с приведенными выше предположениями. Операторы в бесконечномерных гильбертовых пространствах не обязательно должны иметь собственные значения (набор собственных значений не обязательно совпадает со спектром оператора ). Однако все рутинные квантово-механические расчеты можно выполнить, используя физическую формулировку.

Выражения для гамильтониана

Общие формы для одной частицы

Бесплатная частица

Частица не связана никакой потенциальной энергией, поэтому потенциал равен нулю, и этот гамильтониан является самым простым. Для одного измерения:

и в более высоких измерениях:

Постоянно-потенциальная яма

Для частицы в области постоянного потенциала (без зависимости от пространства или времени) в одном измерении гамильтониан имеет вид: V знак равно V 0 <\ displaystyle V = V_ <0>>

Простой гармонический осциллятор

Для простого гармонического осциллятора в одном измерении потенциал изменяется в зависимости от положения (но не времени) в соответствии с:

Для трех измерений это становится

Полная запись гамильтониана показывает, что это просто сумма одномерных гамильтонианов в каждом направлении:

Жесткий ротор

Электростатический или кулоновский потенциал

Электрический диполь в электрическом поле

сам дипольный момент является оператором

Магнитный диполь в магнитном поле

Для частицы со спином 1/2 соответствующий спиновый магнитный момент равен:

μ S знак равно грамм s е 2 м S <\ displaystyle <\ boldsymbol <\ mu>> _ = <\ frac e> <2m>> \ mathbf >

ЧАС ^ знак равно грамм s е 2 м S ⋅ B <\ displaystyle <\ hat > = <\ frac e> <2m>> \ mathbf \ cdot \ mathbf >

Заряженная частица в электромагнитном поле

Π ^ знак равно п ^ + q А <\ displaystyle \ mathbf <\ hat <\ Pi>> = \ mathbf <\ hat

> + q \ mathbf > ,

так что соответствующий оператор кинетической энергии

Преобразование всего этого в гамильтониан дает

Вырождение собственного набора энергии, симметрия и законы сохранения

Уравнения Гамильтона

⟨ п ′ | п ⟩ знак равно δ п п ′ <\ displaystyle \ langle n '| n \ rangle = \ delta _ >

Обратите внимание, что предполагается, что эти базовые состояния не зависят от времени. Предположим, что гамильтониан также не зависит от времени.

Среднее значение гамильтониана этого состояния, которое также является средней энергией, равно

⟨ ЧАС ( т ) ⟩ знак равно d е ж ⟨ ψ ( т ) | ЧАС | ψ ( т ) ⟩ знак равно ∑ п п ′ а п ′ * а п ⟨ п ′ | ЧАС | п ⟩ <\ Displaystyle \ langle H (T) \ rangle \ <\ stackrel <\ mathrm > <=>> \ \ langle \ psi (t) | H | \ psi (t) \ rangle = \ sum _ a_ ^ <*>a_ \ langle n ‘| H | n \ rangle>

Применяя уравнение Шредингера и используя ортонормированность базисных состояний, это далее сводится к

Аналогично можно показать, что

Если мы определим переменные «сопряженного импульса» как π п <\ displaystyle \ pi _ >

тогда приведенные выше уравнения становятся

Источник

ГАМИЛЬТОНИА́Н

Том 6. Москва, 2006, стр. 358

Скопировать библиографическую ссылку:

ГАМИЛЬТОНИА́Н (опе­ра­тор Га­миль­то­на) в кван­то­вой тео­рии, опе­ра­тор пол­ной энер­гии кван­то­вой сис­те­мы, иг­раю­щий важ­ную роль в опи­са­нии её ди­на­ми­ки. В клас­сич. тео­рии ему со­от­вет­ст­ву­ет Га­миль­то­на функ­ция для пол­ной энер­гии сис­те­мы как функ­ции её обоб­щён­ных ко­ор­ди­нат и им­пуль­сов. В кван­то­вой тео­рии функ­ция Га­миль­то­на ста­но­вит­ся опе­ра­то­ром, для по­строе­ния ко­то­ро­го в клас­сич. вы­ра­же­нии ко­ор­ди­на­ты и им­пуль­сы за­ме­ня­ют на со­от­вет­ст­вую­щие опе­ра­то­ры. По­след­ние не ком­му­ти­ру­ют ме­ж­ду со­бой, по­это­му по­ря­док в их про­из­ве­де­ни­ях не­обхо­ди­мо до­оп­ре­де­лить так, что­бы Г. был са­мо­со­пря­жён­ным опе­ра­то­ром. Так, в клас­сич. ме­ха­ни­ке для то­чеч­ной час­ти­цы в по­тен­ци­аль­ном по­ле функ­ция Га­миль­то­на есть сум­ма ки­не­тич. энер­гии (функ­ции им­пуль­са) и по­тен­ци­аль­ной энер­гии (функ­ции ко­ор­ди­нат). В ко­ор­ди­нат­ном пред­став­ле­нии кван­то­вой ме­ха­ни­ки опе­ра­то­ры ком­по­нент им­пуль­са про­пор­цио­наль­ны про­из­вод­ным по ко­ор­ди­на­там, по­это­му опе­ра­тор ки­не­тич. энер­гии с точ­но­стью до ко­эф­фи­ци­ен­та опи­сы­ва­ет­ся опе­ра­то­ром Ла­п­ла­са, а опе­ра­тор по­тен­ци­аль­ной энер­гии – опе­ра­то­ром ум­но­же­ния на со­от­вет­ст­вую­щую функ­цию. Ана­ло­гич­ным об­ра­зом стро­ят­ся Г. и бо­лее слож­ных сис­тем. В кван­то­вой тео­рии по­ля Г. стро­ит­ся на ос­но­ва­нии га­миль­то­но­ва пред­став­ле­ния со­ответ­ст­вую­щей клас­сич. тео­рии по­ля; в этом слу­чае, как пра­ви­ло, ис­поль­зу­ет­ся фо­ков­ское пред­став­ле­ние, в ко­то­ром осн. роль иг­ра­ют опе­ра­то­ры ро­ж­де­ния и унич­то­же­ния кван­тов по­ля. Ес­ли же сис­те­ма во­об­ще не име­ет клас­сич. ана­ло­га, то по­строе­ние Г. осу­ще­ст­в­ля­ет­ся ак­сио­ма­ти­че­ски, ис­хо­дя из фи­зич. смыс­ла этой ве­ли­чи­ны как пол­ной энер­гии.

Источник

Гамильтониан. Оператор энергии.

Напомним основные постулаты квантовой механики, связанные с эрмитовыми операторами:

Оператор, связанный с измерением энергии, в квантовой механике называется оператором Гамильтона или Гамильтонианом. Конкретный вид матрицы Гамильтониана зависит от деталей рассматриваемой системы. Если это система с двумя состояниями типа кубита с двумя базисными векторами, то Гамильтониан имеет вид квадратной матрицы 2х2. В общем случае он может быть и бесконечномерной матрицей.

В классической механике энергия частицы складывается из кинетической \( \displaystyle T\) и потенциальной \( \displaystyle V\). Кинетическая энергия равна:

\( \displaystyle T = \frac<2>= \frac<2m>\) где \( \displaystyle p = mv\) — импульс.

Квантовомеханический аналог получается простой заменой числового значения импульса на оператор:

Сам оператор импульса в квантовомеханическом случае выражается через оператор взятия производной:

Мы получили оператор Гамильтона в координатном базисе:

Его собственные векторы также бесконечномерные — это функции от координаты x. Аппроксимируя вторую производную квадратной матрицей и прибавляя дискретизированную функцию потенциала \( \displaystyle V\) получим конечномерную матрицу, аппроксимирующую Гамильтониан:

Все что остается — это выбрать конкретный вид функции потенциала и найти на компьютере собственные векторы и собственные значения данной матрицы.

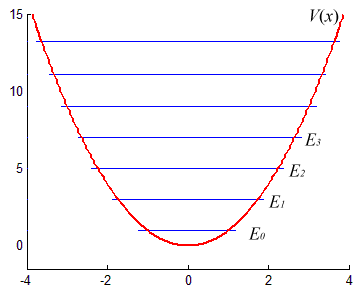
Давайте возьмем квадратичный потенциал \( \displaystyle V = kx^2\), отвечающий линейной силе в классическом случае (пружина, маятник). Система известна как гармонический осциллятор. Найдя собственные значения мы получим, что они отстоят друг от друга на одинаковом расстоянии, причем первый энергетический уровень не нулевой. Квантовый гармонический осциллятор, в отличие от классического, оказывается не может не совершать колебания (иметь нулевую энергию).

Мы наблюдаем эффект квантования. Измеренная энергия не может принимать любое значение, а только одно из разрешенных, дискретных.

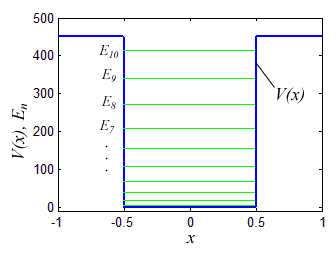
Численные величины собственных значений оператора Гамильтона зависят от вида функции потенциальной энергии. Возьмем, например, второй популярный пример — потенциал в виде прямоугольной ямы.

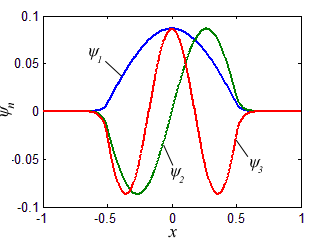
Каждому собственному значению (энергетическому уровню) соответствует собственный вектор — волновая функция в которую перейдет вектор состояния после измерения данного собственного значения (энергии). Несколько собственных функций, соответствующих нескольким первым собственным значениям Гамильтониана с прямоугольным потенциалом приведены на рисунке.

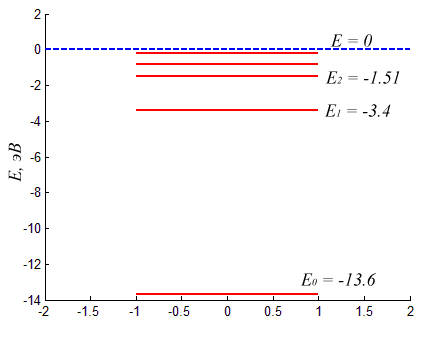
Из рисунка понятно почему квантовомеханический вектор состояния исторически получил название волновой функции. Аналогично можно найти и спектр атома водорода взяв за \( \displaystyle V(x) \) кулоновский потенциал притяжения электрона и протона:

Оператор Гамильтона выделяется среди других эрмитовых операторов тем, что он является генератором эволюции во времени вектора состояния (поэтому он входит в уравнение Шредингера). В связи с этим ряд высказываний касательно времени можно сформулировать используя Гамильтониан. Так утверждение, что величина сохраняется означает ее неизменность с течением времени. На языке оператора Гамильтона данный факт преобразуется в:

Если данный эрмитов оператор коммутирует с Гамильтонианом, то физическая величина, представляемая данным оператором, сохраняется.

То есть, если \( \displaystyle [A,H]=AH-HA=0\), то \( \displaystyle A\) сохраняется.

Тривиальный случай — это закон сохранения энергии, поскольку любой оператор коммутирует сам с собой:

\( \displaystyle [H,H]=0 \Rightarrow\) энергия сохраняется.

Источник

§ 6. Гамильтониан частицы со спином 1/2 в магнитном поле

Обратимся теперь еще к одной системе с двумя состояниями. На этот раз нашим объектом будет частица со спином 1 /₂. Кое-что из того, что мы намерены сказать, затрагивалось уже в предыдущих главах, но повторение поможет нам немного прояснить кое-какие темные места. Покоящийся электрон мы можем считать тоже системой с двумя состояниями. Хотя в этом параграфе мы будем толковать об «электроне», но то, что мы выясним, будет справедливо по отношению ко всякой частице со спином 1 /₂.

Всякое мыслимое состояние |?> электрона можно описать уравнением (8.1), задав амплитуду С₁ того, что электрон находится в состоянии |1>, и амплитуду С₂ того, что он находится в состоянии |2>. Для этого нам понадобится гамильтониан нашей системы с двумя состояниями — электрона в магнитном поле. Начнем с частного случая магнитного поля в направлении z.

(8.17)

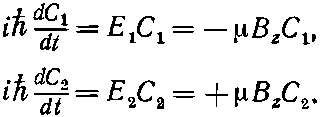
В этом частном случае гамильтониан равен

(8.18)

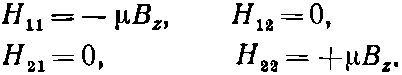
Итак, мы знаем, какой вид имеет гамильтониан, когда магнитное поле направлено по z, и знаем еще энергии стационарных состояний.

А теперь пусть поле не направлено по z. Каков теперь гамильтониан? Как меняются матричные элементы, когда поле не направлено по z? Мы сделаем предположение, что для членов гамильтониана имеется своего рода принцип суперпозиции. Точнее, мы предположим, что если два магнитных поля налагаются одно на другое, то члены гамильтониана просто складываются: если нам известно H_ij для поля, состоящего из одной только компоненты B_z, и известно Н_ij для одной только В_х, то H_ij для поля с компонентами B_z, B_x получится простым сложением. Это бесспорно верно, если рассматриваются только поля в направлении z: если удвоить B_z, то удвоятся и все Н_ij. Итак, давайте допустим, что Н линейно по полю В. Чтобы найти H_ij для какого угодно магнитного поля, больше ничего и не нужно.

Пусть у нас есть постоянное поле В. Мы бы могли провести нашу ось z в направлении поля и обнаружили бы два стационарных состояния с энергиями ±?В. Простой выбор другого направления осей не изменил бы физики дела. Наше описание стационарных состояний стало бы иным, но их энергии по-прежнему были бы ±?B, т. е.

(8.19)

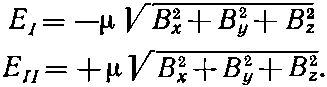
Дальше все уже совсем легко. У нас есть формулы для энергий. Нам нужен гамильтониан, линейный по В_х, В_y и B_z, который даст именно такие энергии, если применить нашу общую формулу (8.3). Задача — найти гамильтониан. Прежде всего заметим, что энергия расщепляется симметрично и ее среднее значение есть нуль. Взглянув на (8.3), мы сразу же увидим, что для этого требуется

(Заметьте, что это подтверждается тем, что нам уже известно при В_x=В_y=0; в этом случае Н₁₁=-?B_z и H₂₂=?B_z.) Если теперь приравнять энергии из (8.3) к тому, что нам известно из (8.19), то получится

(8.20)

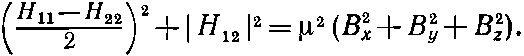
откуда |H₁₂| в этом частном случае равно нулю, что означает, что в H₁₂ не может войти член с В_z. (Вы помните, что мы говорили о линейности всех членов по В_х, В_y и B_z.)

Итак, пока мы узнали, что в Н₁₁ и H₂₂ входят члены с В_z, а в H₁₂ и H₂₁ — нет. Можно попробовать угадать формулы, которые будут удовлетворять уравнению (8.20), написав

(8.21)

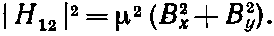
Оказывается, что никак иначе этого сделать нельзя!

«Погодите, — скажете вы, — H₁₂ по В не линейно. Из (8.21) следует, что H₁₂=??(В 2 _x+В 2 _y)». Не обязательно. Есть и другая возможность, которая уже линейна, а именно

На самом деле таких возможностей не одна, в общем случае можно написать

Какой же знак и какую фазу мы обязаны взять? Оказывается, что можно выбрать любой знак и фазу тоже любую, а физические результаты от этого не изменятся. Так что выбор — это вопрос соглашения. Еще до нас кто-то решил ставить знак минус и брать е i? =-1. Мы можем делать так же и написать

(Кстати, эти соглашения связаны и согласуются с тем произволом в выборе фаз, который мы использовали в гл. 4.) Полный гамильтониан для электрона в произвольном магнитном поле, следовательно, равен

(8.22)

(8.23)

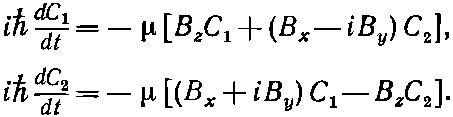
Итак, мы открыли «уравнения движения спиновых состояний» электрона в магнитном поле. Мы угадали их, пользуясь некоторыми физическими аргументами, но истинная проверка всякого гамильтониана заключается в том, что он обязан давать предсказания, согласующиеся с экспериментом. Из всех сделанных проверок следует, что эти уравнения правильны. Более того, хотя все наши рассуждения относились к постоянному полю, написанный нами гамильтониан правилен и тогда, когда магнитные поля меняются со временем. Значит, мы теперь можем применять уравнения (8.23) для решения всевозможных интересных задач.

Источник

СОДЕРЖАНИЕ

Обзор

Координаты фазового пространства (p, q) и гамильтониан H

откуда следует, что

Замечание по терминологии. Некоторые источники определяют преобразование Лежандра как функционал, зависящий от времени.

От уравнения Эйлера-Лагранжа к уравнениям Гамильтона

От принципа стационарного действия к уравнениям Гамильтона

Основная физическая интерпретация

Пример

Лагранжиан этой системы равен

Таким образом, гамильтониан

В терминах координат и импульсов гамильтониан имеет вид

Уравнения Гамильтона дают временную эволюцию координат и сопряженных импульсов в четырех дифференциальных уравнениях первого порядка:

Вывод уравнений Гамильтона

Уравнения Гамильтона можно получить, посмотрев на то, как полный дифференциал от лагранжиана зависит от времени, обобщенные позиции д _я и обобщенные скорости Q _I :

Обобщенные импульсы определялись как

Если это подставить в полный дифференциал лагранжиана, получится

Это можно переписать как

что после перестановки приводит к

Также возможно вычислить полный дифференциал гамильтониана H по времени напрямую, аналогично тому, что было проделано с лагранжианом L выше, давая:

Из двух предыдущих независимых уравнений следует, что их правые части равны между собой. Результат

Поскольку этот расчет был выполнен вне оболочки (т.е. без учета уравнений движения), можно связать соответствующие члены с обеих сторон этого уравнения, чтобы получить:

На оболочке уравнения Лагранжа показывают, что

Перестановка этого дает

∂ L ∂ q я знак равно п ˙ я <\ displaystyle <\ frac <\ partial <\ mathcal >> <\ partial q ^ >> = <\ dot

> _ >

Таким образом, уравнения Гамильтона таковы:

Свойства гамильтониана H

Гамильтониан заряженной частицы в электромагнитном поле

Этот лагранжиан в сочетании с уравнением Эйлера – Лагранжа дает закон силы Лоренца

В канонических импульсах задаются следующим образом:

Обратите внимание, что канонические импульсы не являются калибровочно-инвариантными и физически не измеримыми. Однако кинетический импульс :

калибровочно инвариантен и физически измерим.

Гамильтониан, как преобразование Лежандра лагранжиана, поэтому:

который по-прежнему дает то же уравнение Гамильтона:

В квантовой механике волновая функция также будет подвергаться локальному преобразованию группы U (1) во время калибровочного преобразования, что означает, что все физические результаты должны быть инвариантными относительно локальных преобразований U (1).

Релятивистская заряженная частица в электромагнитном поле

Таким образом, канонический импульс частицы равен

то есть сумма кинетического импульса и потенциального импульса.

Решая для скорости, мы получаем

Это приводит к уравнению силы (эквивалентному уравнению Эйлера – Лагранжа )

из которого можно вывести

От симплектической геометрии к уравнениям Гамильтона

Геометрия гамильтоновых систем.

Гамильтониан может индуцировать симплектическую структуру на гладком четномерном многообразии M 2 n несколькими различными, но эквивалентными способами, наиболее известными из которых являются следующие:

Икс ˙ знак равно J ( d ЧАС ) ( Икс ) <\ displaystyle <\ dot > = J (dH) (x)>

Римановы многообразия

Субримановы многообразия

Непрерывная вещественнозначная группа Гейзенберга представляет собой простой пример субриманова многообразия. Для группы Гейзенберга гамильтониан имеет вид

p _z не входит в гамильтониан.

Алгебры Пуассона

Обобщение на квантовую механику через скобку Пуассона

В частности, более общая форма уравнения Гамильтона гласит

Источник