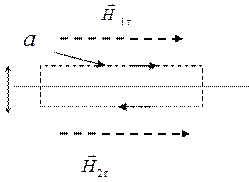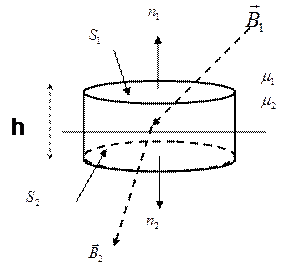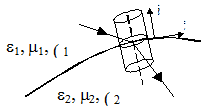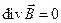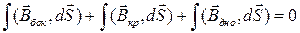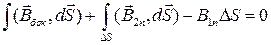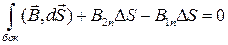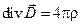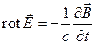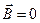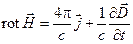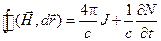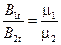граничные условия в магнитном поле
Граничные условия для векторов электрического и магнитного поля на границе раздела двух сред
А) Граничные условия для вектора электрической индукции.
Рассмотрим границу раздела двух сред с различными диэлектрическими проницаемостями 

 |
Рис.1.4.1.Элементарный цилиндр, выделенный на границе раздела двух сред для определения граничных условий на вектор электрической индукции. 

Согласно теореме Гаусса-Остроградского поток вектора электрической индукции 

Устремим высоту цилиндра к нулю 

Где 

Введем поверхностную плотность заряда:

Размерность поверхностной плотности заряда 
Тогда (3.1.2) можно переписать в виде

Если плотность поверхностного заряда равна нулю (

Мы можем сформулировать следующее важное утверждение:
На границе раздела, не содержащей поверхностных зарядов, нормальная составляющая вектора электрической индукции непрерывна.
Б) Граничные условия для вектора магнитной индукции.
Рассмотрим границу раздела двух сред, обладающих различной магнитной проницаемостью. Из тех же соображений, что и в предыдущем пункте и принимая во внимание, что магнитных зарядов не существует, можно записать

Это равенство равносильно следующему утверждению:
На границе раздела двух сред нормальная составляющая вектора магнитной индукции всегда непрерывна.
В) Граничные условия для вектора напряженности электрического поля 
Рассмотрим снова границу раздела двух сред с различными диэлектрическими проницаемостями 

 |
Рис.3.1.2. Контур на границе раздела двух сред, используемый при определении граничных условий для векторов напряженности электрического поля.
Устремим ширину контура 


Откуда следует, что

Это равенство равносильно следующему утверждению:
На границе раздела двух сред касательная составляющая вектора напряженности электрического поля всегда непрерывна.
Г) Граничные условия для вектора напряженности магнитного поля Н.
Как в предыдущем случае выделим на границе раздела двух сред замкнутый контур L (рис.1.4.2). Воспользуемся законом полного тока

Где 
Учтем, что вдоль границы раздела может течь ток проводимости, тогда при стремлении 

Размерность поверхностной плотности тока [
Откуда следует, что

Это равенство равносильно следующему утверждению:
На границе раздела двух сред разность касательных составляющих напряженности магнитного поля равна поверхностной плотности тока.
При отсутствии поверхностного тока

Это равенство равносильно следующему утверждению:
На границе раздела двух сред, по которой не течет поверхностный ток, касательная составляющая магнитного поля непрерывна.
Д) Граничные условия на поверхности идеального проводника.
Определим идеальный проводник, как проводник, внутрь которого не может проникать электромагнитное поле 




Силовые линии электрического поля перпендикулярны к поверхности идеального проводника; силовые линии магнитного поля касательны к поверхности идеального проводника, как показано на рис.3.1.3.
 |
Рис.3.1.3. Силовые линии электрического и магнитного полей вблизи поверхности идеального проводника.
Граничные условия для магнитного поля
Классификация магнетиков.
Дадим краткую характеристику каждого типа магнетика.
Ферромагнетики – особый вид магнетиков, отличающийся от других магнетиков следующими характерными признаками: 1) высоким значением магнитной восприимчивости (см. таблицу); 2) зависимостью магнитной проницаемости μ от напряженности магнитного поля, вследствие чего зависимость 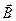
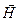
Антиферромагнетики– частный случай ферримагнетиков, в которых магнитные моменты подрешеток с противоположно направленными магнитными моментами полностью компенсируют друг друга (скомпенсированный ферримагнетик). Существование антиферромагнетиков было предсказано Л.Д.Ландау в 1933г. В настоящее время известен широкий спектр веществ, обладающих антиферромагнитными свойствами: редкоземельные элементы (Er, Dy, Ho), оксиды и дифториды некоторых металлов (FeO, MnO, CoF2, NiF2), соли угольной и серной кислот (MnCO3, NiSO4) и другие.
При переходе через границу раздела двух магнетиков с различными магнитными проницаемостями μ1 и μ2 силовые линии магнитного поля испытывают преломление (рис.11.2). Для того, чтобы выяснить, как происходит преломление линий поля необходимо установить для его нормальных и тангенциальных составляющих граничные условия. Вывод граничных условий для магнитного поля в точности аналогичен выводу граничных условий для электрического поля и основывается на применении основных теорем магнитостатики – теоремы Гаусса и теоремы о циркуляции магнитного поля.
Рис.11.2. К выводу граничных условий для магнитного поля.
Для нормальных составляющих индукции 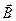
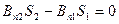
Поток индукции поля через боковую поверхность цилиндра при 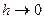
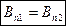
Считая, что по границе раздела магнетиков не текут поверхностные токи (I = 0), будем иметь для тангенциальных составляющих напряженности магнитного поля, согласно теореме о циркуляции поля (рис.11.2):
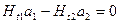
Составляющие циркуляции поля по коротким сторонам контура обхода границы при 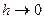
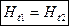
Для построения картины преломления силовых линий поля на границе раздела двух магнетиков к полученным граничным условиям необходимо присоединить еще условия, вытекающие из материального уравнения, связывающего векторы 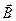
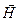
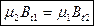
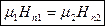
Тем самым, задача о преломлении линий поля полностью решается.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Граничные условия в магнитном поле
Напряженность магнитного поля на границе раздела сред.
Магнитные линии на границе раздела двух сред с различными магнитными проницаемостями претерпевают преломление. Выведем закон этого преломления, получив предварительно весьма важные для практики условия для напряженности МП и магнитной индукции на границе двух сред. При этом ограничимся рассмотрением частного случая равномерного поля в двух однородных средах с магнитными проницаемостями JLlj и JLX2, граничащими по плоской поверхности (рис. 3.5), обозначив углы, составляемые магнитными линиями в одной и второй средах с плоскостью раздела сред [3.5] соответственно через и 02 •
Рис. 3.5. Распределение напряженности однородного МП у плоской границы раздела сред
Рассмотрим замкнутый контур в виде весьма узкого прямоугольника ABCD (рис. 3.5), расположенного у границы раздела сред так, чтобы его длинные стороны АВ и CD оказались в двух разных средах и параллельными плоскости раздела между средами. Применим для этого контура закон полного тока:
Разбивая интеграл по замкнутому контуру (3.28) на четыре интеграла по четырем прямым участкам пути интегрирования и пренебрегая интегралами по весьма коротким участкам ВС и DA по сравнению с интегралами по длинным участкам АВ и CD, будем иметь
величины Н и Н2, COS ОС> и COS 012 вынести из-под интегралов.
Так как оставшиеся интегралы от элементов dl пути интегрирования будут представлять собой длины этих участков, то предыдущее равенство можно записать в виде
Сокращая равенство на равные друг другу отрезки I и /(
выражая углы ОЦ и ОС 2 через исходные углы 0j и 02 ( OCj = 0,5л — 0j, ОС2 — 0,5л + 02 ), получим
т.е. на границе раздела двух сред равны касательные составляющие вектора напряженности магнитного поля.
Магнитная индукция на границе раздела сред. Представим теперь на границе раздела двух сред весьма тонкий параллелепипед (рис. 3.6), две большие грани 5] и ^ которого, параллельные плоскости
раздела, расположены соответственно в первой и второй средах. Запишем для замкнутой поверхности этого параллелепипеда принцип непрерывности магнитных линий:
пренебрегая ввиду малости поверхности S q последним интегралом по сравнению с двумя предыдущими, будем иметь
т. е. на границе раздела двух сред равны нормальные составляющие векторов магнитной индукции.
Рис. 3.6. Распределение индукции однородного МП у плоской границы раздела сред
Закон преломления. Из полученных выше выводов относительно равенства касательных составляющих векторов напряженности МП:
и нормальных составляющих векторов магнитной индукции:
разделив первое равенство на второе, нетрудно получить закон преломления магнитных линий
Таким образом, отношение тангенсов углов падения и преломления магнитных линий при переходе через границу раздела двух сред равно отношению магнитных проницаемостей этих сред.
Направление магнитного поля у поверхности ферромагнитных тел. Остановимся на примере, иллюстрирующем применение последнего закона и раскрывающем весьма важное положение о направлении МП вблизи тел из ферромагнитного материала, в частности вблизи стальных магнитопроводов различных электромагнитных устройств.
В связи с тем, что магнитная проницаемость ферромагнитного вещества во много раз больше магнитной проницаемости материала, обычно окружающего магнитопровод (воздух, масло, пластмасса и т.
д.), различие в тангенсах углов 0j и 02, составляемых магнитными
линиями и нормалью к плоскости раздела сред должно быть также весьма большим. Если, например, в ферромагнитной среде с магнитной
проницаемостью J4 = 100 JLX q магнитная линия будет подходить к
границе раздела почти по касательной (на рис. 4.3 0j =85^), то в воздух эта магнитная линия выйдет почти перпендикулярно поверхности раздела (02 = 5 ). В подавляющем большинстве практических
случаев, когда мы имеем дело с магнитопроводами, выполненными из стали, магнитная проницаемость которой в несколько тысяч раз превышает магнитную проницаемость воздуха, угол 02 выхода магнитных линий из магнитопроводов еще значительно меньше. Поэтому принято считать, что магнитные линии выходят из стальных тел или входят в них практически под прямым углом к их поверхности.
Рассмотрим границу между ферромагнитным материалом и воздухом ()1Ц » JU-2)- В этом случае tgOCj » tgCX 2 ; линия магнитной индукции, подходящая к границе под острым углом в стали, будет выходить в воздухе под углом ОС 2, тангенс которого мал. Практически
можно считать угол ОС 2 близким к нулю; другими словами, линии магнитной индукции выходят из стали в воздух практически по нормали к поверхности стали. Это правило, однако, нельзя распространять на современные материалы для постоянных магнитов, магнитная проницаемость которых мала. Правило действительно лишь в случаях, когда провода с токами, определяющими МП, расположены в воздухе, а не в стали.
Рис. 3.7. Направление МП у границы поверхности ферромагнитного тела
Граничные условия для электрического и магнитного полей



Граничные условия для электрического и магнитного полей определяют поведение нормальных и тангенциальных составляющих напряженностей и индукций электрического и магнитного полей на границе раздела двух сред с различными характеристиками. В простейшем случае эти среды будем считать изотропными, т.е. диэлектрические и магнитные проницаемости будут определены как скалярные величины
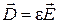
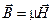
Для определения поведения нормальных к поверхности составляющих путем интегрирования уравнений Максвелла III и IV выберем замкнутую поверхность в виде бесконечно малого цилиндра высотой h и с площадью основания DS, предполагая в дальнейшем устремление каждого из этих параметров к нулю (рис. 4).
Рисунок 4 – замкнутая поверхность в виде бесконечно малого цилиндра
Интегрируя уравнение Максвелла III
по объему и применяя теорему Остроградского-Гаусса, получим
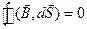
Вычисляя потоки через «дно», «крышку» и «боковую поверхность», получим
Устремим высоту цилиндра к нулю:
– первое граничное уравнение.
Используя 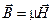
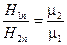
Интегрируя уравнение IV Максвелла
по объему и применяя теорему Остроградского-Гаусса, получим 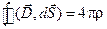
– скачок на заряженной поверхности, вследствие наличия поверхностной плотности электрических зарядов 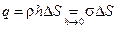
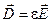
Если поверхностных зарядов нет, то нормальные составляющие индукции электрического поля непрерывны, а – напряженности изменяются по закону
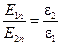
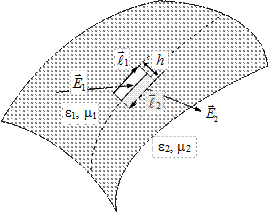
Для определения поведения тангенциальных составляющих поле выберем замкнутый контур, представленный на рис. 4.
Рисунок 5 – бесконечно малый контур
Интегрируя уравнение II Максвелла
по поверхности, натянутой на контур, и применяя к левой части теорему Стокса, получим
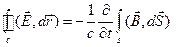
Вычисляя по отдельности циркуляции вдоль каждой из сторон контура и устремляя h®0, получим при
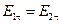
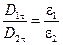
Интегрируя уравнение I Максвелла
по поверхности, натянутой на контур, и применяя к левой части теорему Стокса, получим
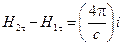
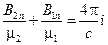
где i – линейная плотность поверхностных токов.
Если отсутствуют поверхностные токи i = 0, то