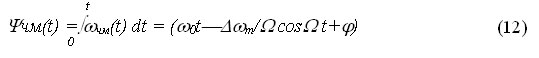характеристики и параметры модулированных сигналов

Измерение параметров модулированных сигналов

МОДУЛИРОВАННЫХ СИГНАЛОВ

Параметры модулированных сигналов

Модуляцией называется физический процесс преобразования несу- щего сигнала, при котором один из параметров его подвергается изменению, соответствующему закону информативного сигнала.

Несущий сигнал, параметр которого подвергнут изменению, называют модулированным, а сигнал, в соответствии с законом измерения которого производят модуляцию, — модулирующим.

Рассмотрим наиболее часто встречающийся случай, когда в качестве несущего используется синусоидальный сигнал вида

В зависимости от того, какой параметр данного сигнала подвергается изменению, различают следующие виды модуляции:

Модуляцию двух последних видов вследствие существующей тесной связи между ними часто объединяют под единым термином «угловая модуляция».

Рассмотрим основные параметры модулированных сигналов. Обозначим модулирующий сигнал в виде функции т (t). При амплитудной модуляции сигнала (10.1) имеем

Если модулирующий сигнал т (t) является гармоническим, т. е.

В более общем случае, соответствующем реальным (квазисинусои- дальным) модулирующим сигналам, имеем

В этом случае AM-сигнал принимает вид

AM-сигнал, описываемый формулой (10.6), за период модуляции Т имеет максимальное U_max и минимальное U_mm значения амплитуды колебания (соответственно есть максимальное и минимальное значение огибающей сигнала). Величина М_в и М_н, %, соответственно равны

и называются коэффициентом модуляции «вверх» (М_в) и коэффициентом модуляции «вниз» (М_н). Коэффициенты модуляции М_в и М_н называются иногда коэффициентами пиковой модуляции.

В частном случае модуляции гармоническим сигналом (10.3) имеем М_в = М_И = MQ.

В отличие от (10.1) реальные модулируемые сигналы характеризуются наличием высших гармонических составляющих, т. е.

где U„ и ф„- соответственно амплитуда и начальная фаза п-й гармонической составляющей.

В этом случае AM-сигнал имеет вид

Такой сигнал в общем случае имеет различные по форме огибающие положительной и отрицательной полуволн несущего колебания и, следовательно, должен характеризоваться различными коэффициентами модуляции М_в и М_н для каждой из полуволн. Это обстоятельство должно приниматься во внимание при измерении коэффициента модуляции средств измерений, имеющими разное схемное построение, особенно в метрологической практике.

При ЧМ-модуляции изменению в соответствии с законом т (t) подвергается несущая частота сигнала, т. е./(0 =fo + т (t).

В случае AM-модуляции сигналом (10.2) имеем

Величина А/ называется девиацией частоты. Переходя к круговой частоте, получим

Используя общую формулу для фазы колебания с переменной частотой

получаем выражение для ЧМ-сигнала

При модуляции сигналом (10.5) выражение ЧМ-сигнала примет следующий вид:

где р? = Асо₀ / Ю — индекс парциальной частотной модуляции.

В этом случае вводятся параметры ЧМ-сигнала: девиация частоты «вверх» (А/^), равная максимальному (пиковому) отклонению частоты от среднего значения в сторону ее увеличения, и девиация частоты «вниз» (Д/н), равная максимальному отклонению частоты в сторону меньших значений.

При модуляции гармоническим сигналом (10.3) имеем

Одним из наиболее важных параметров модулированных сигналов является уровень искажения закона модуляции.

Источник

Измерение формы и спектра сигналов

Измерение параметров модулированных сигналов

В радиотехнических устройствах применяются амплитудная, частотная, угловая (фазовая), импульсная и комбинированные виды модуляции. В первых трех видах модуляции амплитуда, частота или фаза синусоидального сигнала изменяется по закону изменения модулирующего напряжения. При импульсной модуляции модулирующее напряжение воздействует на видеоимпульсы и изменяет их высоту, частоту следования, длительность, а также их временное положение или относительную фазу.

Выражение для сигнала, модулированного по амплитуде синусоидальным напряжением, имеет следующий вид:

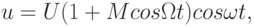( 10.9)

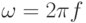
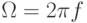
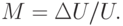где U – амплитуда немодулированного высокочастотного колебания, , f – несущая частота, , F – модулирующая частота, M – коэффициент модуляции, равен отношению изменения амплитуды высокочастотного колебания при модуляции последнего к ее значению в отсутствие модуляции:

( 10.10)

Максимальное изменение амплитуды не должно превышать ее значения, следовательно, максимальное значение M = 1, минимальное M=0.

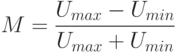( 10.11)

Формулы (10.10) и (10.11) справедливы только для симметричной модуляции. Для оценки асимметрии коэффициента модуляции измеряется раздельно «вверх» и «вниз»

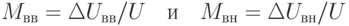( 10.12)

Коэффициент амплитудной модуляции измеряют двумя методами: осциллографическим и методом выпрямления.

Осциллографический метод осуществляют способом линейной и синусоидальной разверток. При линейной развертке в канал вертикального отклонения подают высокочастотный модулированный сигнал, а частоту развертки устанавливают в 2-3 раза ниже модулирующей частоты. На экране осциллографа появляется осциллограмма модулированного сигнала в виде .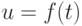

Для определения коэффициента модуляции при синусоидальной развертке в канал вертикального отклонения подают модулированный сигнал, а в канал горизонтального отклонения – модулирующее напряжение.

Метод выпрямления применяют для измерения коэффициента модуляции в процессе эксплуатации. Сущность метода заключается в том, что высокочастотный модулированный сигнал сначала детектируется, а затем измеряется стрелочными приборами постоянного и переменного тока. Приборы, основанные на этом методе, называются измерителями модуляции.

Самый распространенный способ выпрямления – способ двойного детектирования. Модулированный сигнал сначала детектируется линейным, а затем пиковым детектором. При линейном детектировании на нагрузке создается пульсирующее напряжение, постоянная составляющая которого соответствует напряжению несущей частоты U и фиксируется при помощи стрелочного индикатора. 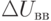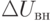Переменная составляющая, соответствующая огибающей модулированного колебания, поступает на пиковый вольтметр с закрытым входом, показания которого в зависимости от положения переключателя П пропорциональны амплитуде или .

Коэффициент модуляции M определяют по формуле (10.12).

Выражение для сигнала, модулированного по частоте одним синусоидальным напряжением, имеет вид:

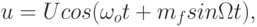( 10.13)

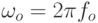
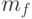
где U – амплитуда высокочастотного колебания, , f – значение высокой (несущей) частоты до модуляции, , F – частота модулирующего напряжения, – индекс частотной модуляции,

( 10.14)

где – отклонение высокой частоты при модуляции – девиация частоты.

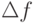
Девиацию частоты можно измерить несколькими методами, наиболее распространенный – метод частотного детектора. Сущность его состоит в том, что частотно-модулированные колебания преобразуются в амплитудно-модулированные, а затем детектируются амплитудным детектором, в результате чего получается напряжение, пропорциональное напряжению модулирующей частоты. Это напряжение измеряется пиковым вольтметром.

Частотно-модулированные колебания преобразуются в колебания низкой частоты частотным детектором, амплитудно-частотная характеристика которого имеет вид S-образной кривой.

Модулированный по частоте сигнал преобразуется в сигнал промежуточной частоты, усиливается до уровня, необходимого для нормальной работы ограничителя, и поступает на частотный детектор, выходное напряжение которого пропорционально девиации частоты; это напряжение проходит через фильтр нижних частот, усиливается и измеряется пиковым вольтметром. Шкала последнего проградуирована в единицах девиации – килогерцах.

Источник

Теория радиоволн: аналоговая модуляция

Амплитудная модуляция

При амплитудной модуляции, огибающая амплитуд несущего колебания изменяется по закону, совпадающему с законом передаваемого сообщения. Частота и фаза несущего колебания при этом не меняется.

Одним из основных параметров АМ, является коэфициент модуляции(M).
Коэффициент модуляции — это отношение разности между максимальным и минимальным значениями амплитуд модулированного сигнала к сумме этих значений(%).
Проще говоря, этот коэффициент показывает, насколько сильно значение амплитуда несущего колебания в данный момент отклоняется от среднего значения.
При коэффициенте модуляции больше 1, возникает эффект перемодуляции, в результате чего происходит искажение сигнала.

Данный спектр свойственен для модулирующего колебания постоянной частоты.

На графике, по оси Х представлена частота, по оси У — амплитуда.
Для АМ, кроме амплитуды основной частоты, находящейся в центре, представлены также значения амплитуд справа и слева от частоты несущей. Это так называемые левая и правая боковые полосы. Они отнесены от частоты несущей на расстояние равное частоте модуляции.
Расстояние от левой до правой боковой полосы называют ширина спектра.
В нормальном случае, при коэффициенте модуляции

Источник

Что такое модуляция и разновидности модулированных сигналов?

Общие сведения о модуляции

Модуляция — это процесс преобразования одного или нескольких информационных параметров несущего сигнала в соответствии с мгновенными значениями информационного сигнала.

В результате модуляции сигналы переносятся в область более высоких частот.

Использование модуляции позволяет:

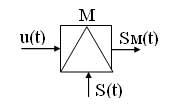
Модуляция осуществляется в устройствах модуляторах. Условное графическое обозначение модулятора имеет вид:

При модуляции на вход модулятора подаются сигналы:

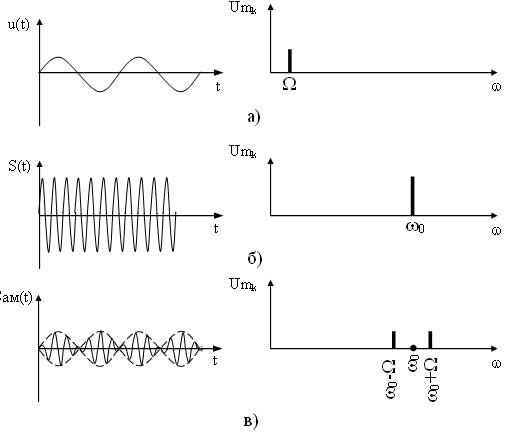
u(t) — модулирующий, данный сигнал является информационным и низкочастотным (его частоту обозначают W или F);

S(t) — модулируемый (несущий), данный сигнал является неинформационным и высокочастотным (его частота обозначается w₀ или f₀);

Sм(t) — модулированный сигнал, данный сигнал является информационным и высокочастотным.

В качестве несущего сигнала может использоваться:

Так как в процессе модуляции изменяются информационные параметры несущего колебания, то название вида модуляции зависит от изменяемого параметра этого колебания.

1. Виды аналоговой модуляции:

2. Виды импульсной модуляции:

Амплитудная модуляция

Амплитудная модуляция — процесс изменения амплитуды несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.

Рассмотрим математическую модель амплитудно-модулированного (АМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала

на несущее колебание

происходит изменение амплитуды несущего сигнала по закону:

где а_ам — коэффициент пропорциональности амплитудной модуляции.

Подставив (3) в математическую модель (2) получим:

Вынесем Um за скобки:

Отношение а_ам Um_u/Um = m_ам называется коэффициентом амплитудной модуляции. Данный коэффициент не должен превышать единицу, т. к. в этом случае появляются искажения огибающей модулированного сигнала называемые перемодуляцией. С учетом m_ам математическая модель АМ сигнала при гармоническом модулирующем сигнале будет иметь вид:

Если модулирующий сигнал u(t) является негармоническим, то математическая модель АМ сигнала в этом случае будет иметь вид:

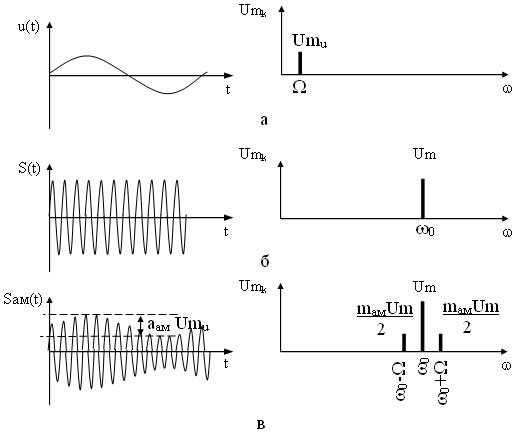
Рассмотрим спектр АМ сигнала для гармонического модулирующего сигнала. Для этого раскроем скобки математической модели модулированного сигнала, т. е. представим его в виде суммы гармонических составляющих.

Как видно из выражения в спектре АМ сигнала присутствует три составляющих: составляющая несущего сигнала и две составляющих на комбинационных частотах. Причем составляющая на частоте ?₀—? называется нижней боковой составляющей, а на частоте ?₀ + ? — верхней боковой составляющей. Спектральные и временные диаграммы модулирующего, несущего и амплитудно-модулированного сигналов имеют вид (рисунок 2).

Ширина спектра для данного сигнала будет определятся

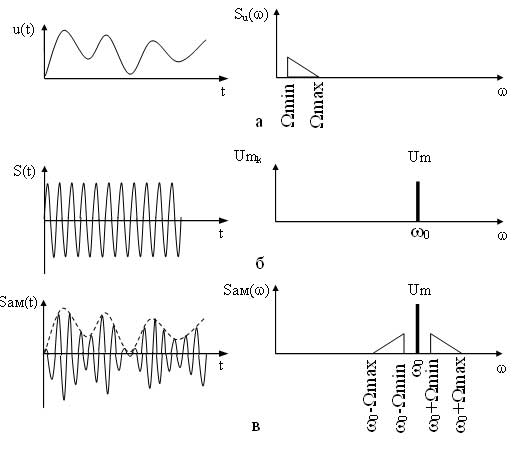
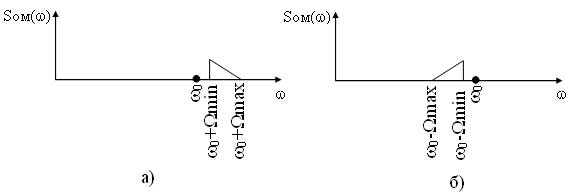
Если же модулирующий сигнал является случайным, то в этом случае в спектре составляющие модулирующего сигнала обозначают символически треугольниками (рисунок 3).

Ширина спектра для данного сигнала будет определятся

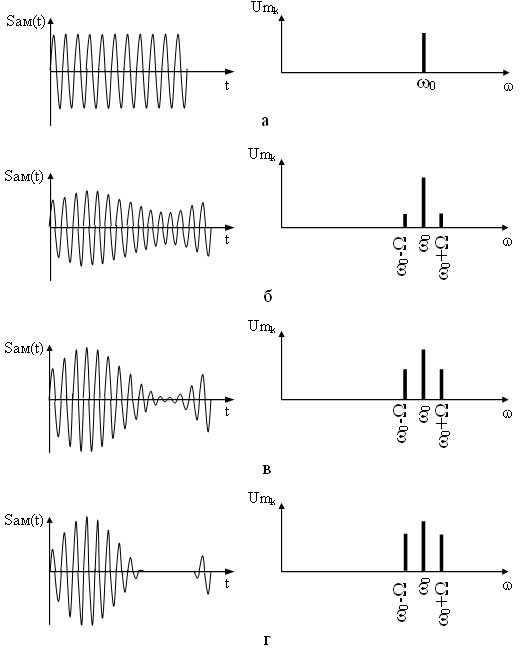
На рисунке 4 приведены временные и спектральные диаграммы АМ сигналов при различных индексах m_ам. Как видно при m_ам=0 модуляция отсутствует, сигнал представляет собой немодулированную несущую, соответственно и спектр этого сигнала имеет только составляющую несущего сигнала (рисунок 4,

а), при индексе модуляции m_ам=1 происходит глубокая модуляция, в спектре АМ сигнала амплитуды боковых составляющих равны половине амплитуды составляющей несущего сигнала (рисунок 4в), данный вариант является оптимальным, т. к. энергия в большей степени приходится на информационные составляющие. На практике добиться коэффициента равного едините тяжело, поэтому добиваются соотношения 0 1 происходит перемодуляция, что, как отмечалось выше, приводит к искажению огибающей АМ сигнала, в спектре такого сигнала амплитуды боковых составляющих превышают половину амплитуды составляющей несущего сигнала (рисунок 4г).

Основными достоинствами амплитудной модуляции являются:

Недостатками этой модуляции являются:

Амплитудная модуляция нашла широкое применение:

Балансная и однополосная модуляция

Как отмечалось выше, одним из недостатков амплитудной модуляции является наличие составляющей несущего сигнала в спектре модулированного сигнала. Для устранения этого недостатка применяют балансную модуляцию. При балансной модуляциипроисходит формирование модулированного сигнала без составляющей несущего сигнала. В основном это осуществляется путем использования специальных модуляторов: балансного или кольцевого. Временная диаграмма и спектр балансно-модулированного (БМ) сигнала представлен на рисунке 5.

Также особенностью модулированного сигнала является наличие в спектре двух боковых полос несущих одинаковую информацию. Подавление одной из полос позволяет уменьшить спектр модулированного сигнала и, соответственно, увеличить число каналов в линии связи. Модуляция при которой формируется модулированный сигнал с одной боковой полосой (верхней или нижней) называется однополосной. Формирование однополосно-модулированного (ОМ) сигнала осуществляется из БМ сигнала специальными методами, которые рассматриваются ниже. Спектры ОМ сигнала представлены на рисунке 6.

Частотная модуляция

Частотная модуляция — процесс изменения частоты несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.

Рассмотрим математическую модель частотно-модулированного (ЧМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала

на несущее колебание

происходит изменение частоты несущего сигнала по закону:

где а_чм — коэффициент пропорциональности частотной модуляции.

Величина Dw_m называется девиацией частоты. Следовательно, девиация частоты показывает наибольшее отклонение частоты модулированного сигнала от частоты несущего сигнала.

называется индексом частотной модуляции.

Учитывая (12) и (13) математическая модель ЧМ сигнала при гармоническом модулирующем сигнале будет иметь вид:

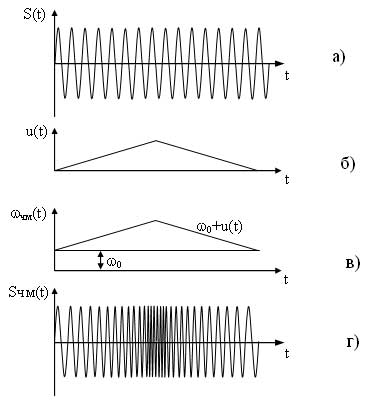
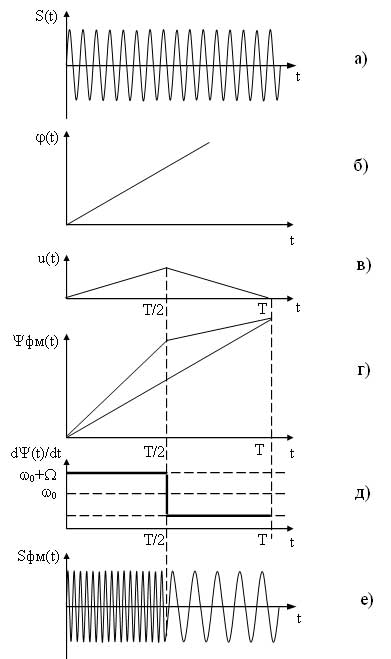
Временные диаграммы, поясняющие процесс формирования частотно-модулированного сигнала приведены на рисунке 7. На первых диаграммах а) и б) представлены соответственно несущий и модулирующий сигналы, на рисунке в) представлена диаграмма показывающая закон изменения частоты ЧМ сигнала. На диаграмме г) представлен частогтно-модулированный сигнал соответствующий заданному модулирующему сигналу, как видно из диаграммы любое изменение амплитуды модулирующего сигнала вызывает пропорциональное изменение частоты несущего сигнала.

Для построения спектра ЧМ сигнала необходимо разложить его математическую модель на гармонические составляющие. В результате разложения получим

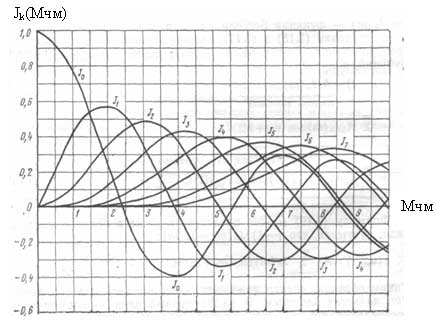
где J_k(Mчм) — коэффициенты пропорциональности.

J_k(Mчм) определяются по функциям Бесселя и зависят от индекса частотной модуляции. На рисунке 8 представлен график содержащий восемь функций Бесселя. Для определения амплитуд составляющих спектра ЧМ сигнала необходимо определить значение функций Бесселя для заданного индекса. Причем как

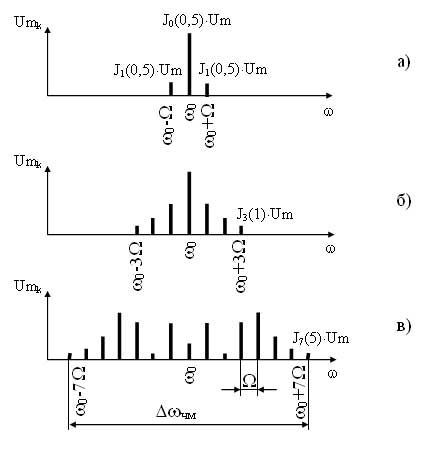
видно из рисунка различные функции имеют начало в различных значениях Мчм, а следовательно, количество составляющих в спектре будет определятся Мчм (с увеличивается индекса увеличивается и количество составляющих спектра). Например необходимо определить коэффициенты J_k(Мчм) при Мчм=2. По графику видно, что при заданном индексе можно определить коэффициенты для пяти функций (J₀, J₁, J₂, J₃, J₄) Их значение при заданном индексе будет равно: J₀=0,21; J₁=0,58; J₂=0,36; J₃=0,12; J₄=0,02. Все остальные функции начинаются после значения Мчм=2 и равны, соответственно, нулю. Для приведенного примера количество составляющих в спектре ЧМ сигнала будет равно 9: одна составляющая несущего сигнала (Um J₀) и по четыре составляющих в каждой боковой полосе (Um J₁; Um J₂; Um J₃; Um J₄).

Еще одной важной особенностью спектра ЧМ сигнала является то, что можно добиться отсутствия составляющей несущего сигнала или сделать ее амплитуду значительно меньше амплитуд информационных составляющих без дополнительных технических усложнений модулятора. Для этого необходимо подобрать такой индекс модуляции Мчм, при котором J₀(Мчм) будет равно нулю (в месте пересечения функции J₀ с осью Мчм), например Мчм=2,4.

Достоинством частотной модуляции являются:

Основным недостатком данной модуляции является большая ширина спектра модулированного сигнала.

Частотная модуляция используется:

Фазовая модуляция

Фазовая модуляция — процесс изменения фазы несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.

Рассмотрим математическую модель фазо-модулированного (ФМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала

на несущее колебание

происходит изменение мгновенной фазы несущего сигнала по закону:

где а_фм — коэффициент пропорциональности частотной модуляции.

Подставляя ?фм(t) в S(t) получаем математическую модель ФМ сигнала при гармоническом модулирующем сигнале:

Произведение а_фм Um_u=Dj_m называется индексом фазовой модуляции или девиацией фазы.

Поскольку изменение фазы вызывает изменение частоты, то используя (11) определяем закон изменения частоты ФМ сигнала:

Произведение а_фмUm_u?=??_m является девиацией частоты фазовой модуляции. Сравнивая девиацию частоты при частотной и фазовой модуляциях можно сделать вывод, что и при ЧМ и при ФМ девиация частоты зависит от коэффициента пропорциональности и амплитуды модулирующего сигнала, но при ФМ девиация частоты также зависит и от частоты модулирующего сигнала.

Временные диаграммы поясняющие процесс формирования ФМ сигнала приведены на рисунке 10.

Ширина спектра ФМ сигнала определяется выражением:

Достоинствами фазовой модуляции являются:

Дискретная двоичная модуляция (манипуляция гармонической несущей)

Дискретная двоичная модуляция (манипуляция) — частный случай аналоговой модуляции, при которой в качестве несущего сигнала используется гармоническая несущая, а в качестве модулирующего сигнала используется дискретный, двоичный сигнал.

Различают четыре вида манипуляции:

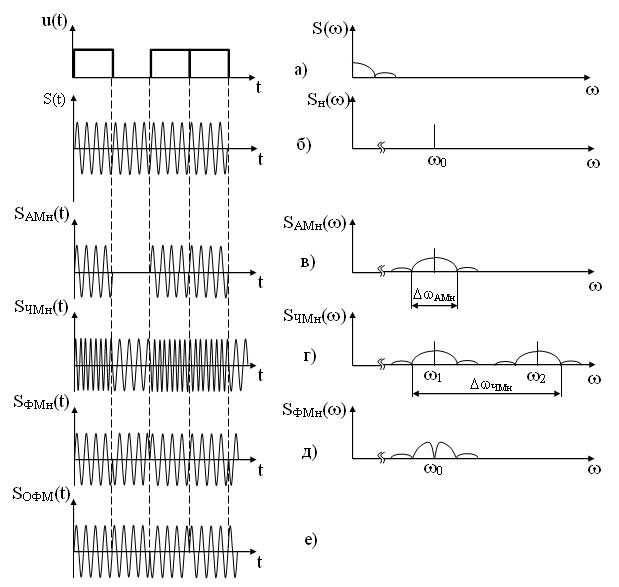
Временные и спектральные диаграммы модулированных сигналов при различных видах манипуляции представлены на рисунке 11.

При амплитудной манипуляции, также как и при любом другом модулирующем сигнале огибающая S_АМн(t) повторяет форму модулирующего сигнала (рисунок 11, в).

При фазовой манипуляции фаза несущего сигнала изменяется на 180° в момент изменения амплитуды модулирующего сигнала. Если следует серия из нескольких импульсов, то фаза несущего сигнала на этом интервале не изменяется (рисунок 11, д).

При относительно-фазовой манипуляции фаза несущего сигнала изменяется на 180° лишь в момент подачи импульса, т. е. при переходе от активной паузы к посылке (0?1) или от посылке к посылке (1?1). При уменьшении амплитуды модулирующего сигнала фаза несущего сигнала не изменяется (рисунок 11, е). Спектры сигналов при ФМн и ОФМн имеют одинаковый вид (рисунок 9, е).

Сравнивая спектры всех модулированных сигналов можно отметить, что наибольшую ширину имеет спектр ЧМн сигнала, наименьшую — АМн, ФМн, ОФМн, но в спектрах ФМн и ОФМн сигналов отсутствует составляющая несущего сигнала.

В виду большей помехоустойчивости наибольшее распространение получили частотная, фазовая и относительно-фазовая манипуляции. Различные их виды используются в телеграфии, при передаче данных, в системах подвижной радиосвязи (телефонной, транкинговой, пейджинговой).

Импульсная модуляция

Импульсная модуляция — это модуляция, при которой в качестве несущего сигнала используется периодическая последовательность импульсов, а в качестве модулирующего может использоваться аналоговый или дискретный сигнал.

Поскольку периодическая последовательность характеризуется четырьмя информационными параметрами (амплитудой, частотой, фазой и длительностью импульса), то различают четыре основных вида импульсной модуляции:

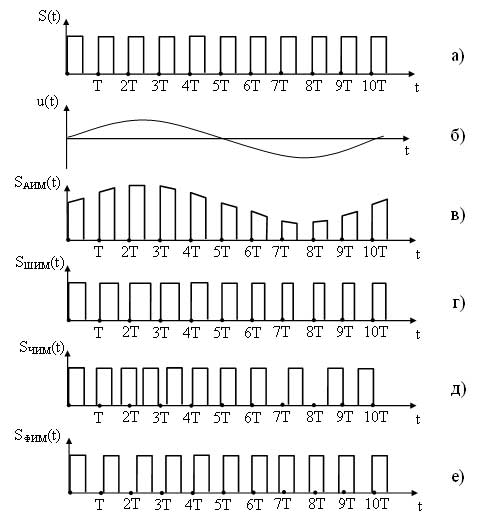
Временные диаграммы импульсно-модулированных сигналов представлены на рисунке 12.

При АИМ происходит изменение амплитуды несущего сигнала S(t) в соответствии с мгновенными значениями модулирующего сигнала u(t), т. е. огибающая импульсов повторяет форму модулирующего сигнала (рисунок 12, в).

При ШИМ происходит изменение длительности импульсов S(t) в соответствии с мгновенными значениями u(t) (рисунок 12, г).

При ЧИМ происходит изменение периода, а соответственно и частоты, несущего сигнала S(t) в соответствии с мгновенными значениями u(t) (рисунок 12, д).

При ФИМ происходит смещение импульсов несущего сигнала относительно их тактового (временного) положения в немодулированной несущей (тактовые моменты обозначены на диаграммах точками Т, 2Т, 3Т и т. д.). ФИМ сигнал представлен на рисунке 12, е.

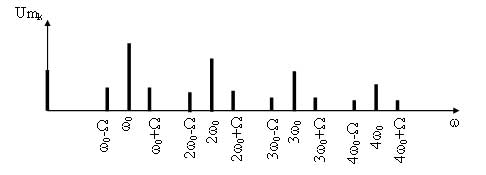
Поскольку при импульсной модуляции переносчиком сообщения является периодическая последовательность импульсов, то спектр импульсно-модулированных сигналов является дискретным и содержит множество спектральных составляющих. Этот спектр представляет собой спектр периодической последовательности импульсов в котором возле каждой гармонической составляющей несущего сигнала находятся составляющие модулирующего сигнала (рисунок 13). Структура боковых полос возле каждой составляющей несущего сигнала зависит от вида модуляции.

Также важной особенностью спектра импульсно-модулированных сигналов является то, что ширина спектра модулированного сигнала, кроме ШИМ, не зависит от модулирующего сигнала. Она полностью определяется длительностью импульса несущего сигнала. Поскольку при ШИМ длительность импульса изменяется и зависит от модулирующего сигнала, то при этом виде модуляции и ширина спектра также зависти от модулирующего сигнала.

Частоту следования импульсов несущего сигнала может быть определена по теореме В. А. Котельникова как f₀ =2Fmax. При этом Fmax это верхняя частота спектра модулирующего сигнала.

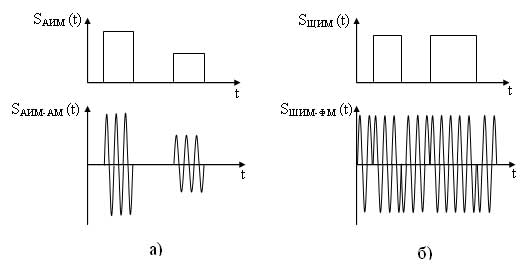
Передача импульсно модулированных сигналов по высокочастотным линиям связи невозможна, т. к. спектр этих сигналов содержит низкочастотные составляющий. Поэтому для передачи осуществляют повторную модуляцию. Это модуляция, при которой в качестве модулирующего сигнала используют импульсно-модулированный сигнал, а в качестве несущего гармоническое колебание. При повторной модуляции спектр импульсно-модулированного сигнала переносится в область несущей частоты. Для повторной модуляции может использоваться любой из видов аналоговой модуляции: АМ, ЧС, ФМ. Полученная модуляция обозначается двумя аббревиатурами: первая указывает на вид импульсной модуляции а вторая — на вид аналоговой модуляции, например АИМ-АМ (рисунок 14, а) или ШИМ-ФМ (рисунок 14, б) и т. д.

Источник