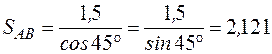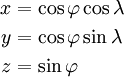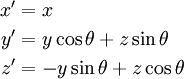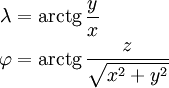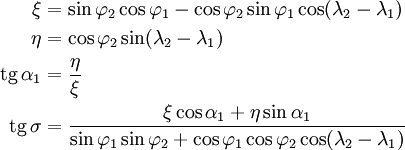какие исходные данные требуются для решения обратной геодезической задачи
GIS-LAB
Географические информационные системы и дистанционное зондирование
Задачи на сфере: обратная геодезическая задача
Обратная геодезическая задача — это нахождение начального направления и расстояния между двумя точками с известными координатами.
Содержание
[править] Общие положения
В качестве модели Земли принимается сфера с радиусом R, равным среднему радиусу земного эллипсоида. Аналогом прямой линии на плоскости является геодезическая линия на поверхности. На сфере геодезическая линия — дуга большого круга.
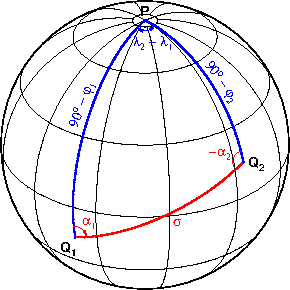
Введём следующие обозначения:
Линейное расстояние по дуге большого круга s связано со сферическим расстоянием σ формулой s = R σ.
Прямая и обратная геодезические задачи являются важными элементами более сложных геодезических задач.
[править] Постановка задачи
На рисунке синим цветом выделены заданные элементы сферического треугольника, красным цветом неизвестные.
[править] Алгоритм
Существует великое множество подходов к решению поставленной задачи. Рассмотрим простой и надёжный векторный метод.
Можно устранить второй пункт, если в первом заменить долготу λ₂ на разность долгот (λ₂ − λ₁).
Пример реализации алгоритма в виде функции языка Си:
Следует заметить, что прямая и обратная задача математически идентичны, и алгоритмы их решения зеркально отражают друг друга.
[править] Преобразование сферических координат в декартовы
В данном случае в качестве сферических координат φ, λ подставим φ₂, λ₂.
[править] Вращение вокруг оси
Представим оператор вращения вокруг оси X на угол θ в следующем виде:
Операторы вращения вокруг осей Y и Z получаются перестановкой символов.
Реализация вращения вокруг i-ой координатной оси на Си:
[править] Преобразование декартовых координат в сферические
В данном случае в роли сферических координат φ, λ окажутся углы (90° − σ), (180° − α₁).
[править] Пример программной реализации
Исходники вышеприведённых функций можно найти в архиве Sph.zip в файле sph.c. Кроме того, в файл sph.h включены следующие определения:
Теперь напишем программу, которая обращается к функции SphereInverse для решения обратной задачи:
В архиве Sph.zip этот код находится в файле inv.c. Создадим исполняемый модуль inv компилятором gcc:
Впрочем, в архиве есть Makefile. Для MS Windows готовую программу inv.exe можно найти в архиве Sph-win32.zip.
Программа читает данные из стандартного ввода консоли и отправляет результаты на стандартный вывод. Для чтения и записи файлов используются символы перенаправления потока «>» и « [править] Решение обратной задачи средствами PROJ
В пакет PROJ входит программа geod, предназначенная для решения прямых и обратных геодезических задач на сфере. Так выглядит команда обработки файла inv.dat:
Параметр +a определяет радиус сферы, -I — решение обратных задач, -f — формат вывода угловых величин, -F — формат вывода длин линий, +units — единица измерения расстояний. В результате получим идентичный вывод:
Различие значений α₂ на 360° объясняется тем, что inv выводит азимуты в диапазоне от 0° до 360°, а geod от −180° до +180°.
[править] Альтернативные методы
Некоторые элементы альтернативных методов решения обратной задачи представлены в статье Вычисление расстояния и начального азимута между двумя точками на сфере.
В большинстве своём другие методы основаны на сферической тригонометрии. Многие из них используют вычисление σ или α₁ по таким функциям, как синус, косинус или гаверсинус. Это приводит к неоднозначности результатов вблизи особых значений, когда производная функции равна нулю. Такие методы не могут считаться универсальными.
К наиболее надёжным относится следующий способ:
В сферической тригонометрии углы и стороны должны быть в диапазоне [0, 180°]. Алгоритмизация формул требует анализа и обработки случаев, когда входные величины не попадают в эти рамки.
[править] Ссылки
Последнее обновление: 2020-05-10 07:46
Дата создания: 11.03.2014
Автор(ы): ErnieBoyd
ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА. Методические указания с вариантами для решения.
Методические указания предназначены для обеспечения самостоятельной работы студентов при решении Обратной геодезической задачи.
Просмотр содержимого документа
«ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА. Методические указания с вариантами для решения.»
Обратная геодезическая задача.
Порядок выполнения работы………………………………….5
Список использованной литературы…………………………24
Методические указания предназначены для обеспечения самостоятельной работы студентов при решении Обратной геодезической задачи. Данная задача широко представлена, как на втором, так и на третьем курсах специальности
№ 120301 «Землеустройство». В методических указаниях подробно рассмотрен порядок решения обратной геодезической задачи. Для обеспечения самостоятельной работы прилагается 100 вариантов для решения задачи, с ответами (приложения №1,2). Данная работа поможет преподавателю, так как раздаточного материала хватит на три учебных группы и все варианты имеют ответы.
Цель работы – оказать помощь студентам при самостоятельном решении Обратной геодезической задачи.
Согласно Государственного образовательного стандарта СПО студент должен:
иметь представление о сфере применения данной задачи;
знать способы решения обратной геодезической задачи;
уметь правильно оформить результаты вычислений и произвести контроль с использованием вычислительной техники.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Раздел IX. Геодезические работы при землеустройстве.
Тема 9.3 Геодезические работы при перенесении проектов внутрихозяйственного землеустройства в натуру.
Практическая работа. Решение обратных геодезических задач при подготовке геоданных для перенесения проекта в натуру.
Задание: выполнить решение обратных геодезических задач для подготовки геоданных.
Исходные данные: приложение №1, по вариантам.
Обратная геодезическая задача.


Для вычисления румба в градусной мере необходимо выполнить на микрокалькуляторе следующие операции:
4. Дирекционный угол линии АВ (αАВ)
в

Формулы для вычисления дирекционного угла линии по румбу.
8. 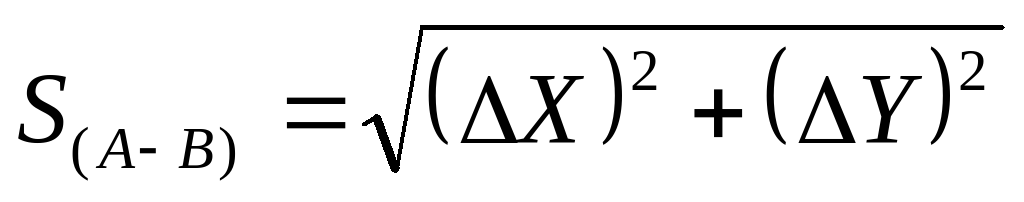
9. SAB ср. вычисляется, как среднее из трёх
полученных значений расстояния АВ.

XA = 28359.109 м 1. X = XB – XA=29007.458 – 28359.109 = 648.349м.
YA = 29408.251 м 2. Y = YB – YA=29903.074 – 29408.251 = 494.823м.
XB = 29007.458 м 3. tg (rАВ) = ΔY : ΔX = 0.7632047;
YB = 29903.074 м 4. rАВ = СВ : 37 ˚ 21 ´ 03. ´´ 8 ;

8. 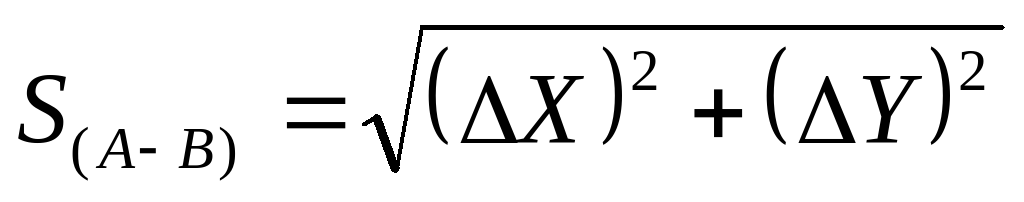
Образец формуляра для решения обратной геодезической задачи.
Решение обратной геодезической задачи
Обратная геодезическая задача
Обратная геодезическая задача заключается в том, что при известных координатах точек А( XA, YA ) и В( XB, YB ) необходимо найти длину SAB и направление линии АВ: румб rAB и дирекционный угол αAB (рис.24).
Рис. 24. Обратная геодезическая задача
Даннная задача решается следующим образом.
Сначала находим приращения координат:
Величину угла rAB определем из отношения
По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название. Используя зависимость между дирекционными углами и румбами, находим αAB.
Для контроля расстояние SAB дважды вычисляют по формулам:
SAB= ΔX = ΔY = ΔX · sec αAB = ΔY · cosec αAB
SAB= ΔX = ΔY = ΔX · sec rAB = ΔY · cosec rAB
Расстояние SAB можно определить также по формуле
Решение прямой геодезической задачи выполнятеся при помощи следующих формул:
Исходными данными для решения обратной геодезической задачи (определение расстояния между точками и дирекционного угла направления 1-2) являются координаты точек 1 и 2. Инфо
Решение обратной геодезической задачи выполняется при помощи следующи формул:
Правильность вычисления дирекционного угла можно проконтролировать начертив схему с взаимным отображением точек 1 и 2. Если вычисленный по формуле угол не соответсвует схеме, то к полученному значению угла следует прибавить или отнять 180 градусов.
20. (17.1.)
Для определения площади земельных участков существуют различные способы. Применение того или иного способа зависит от наличия планово-картографического материала, значимости и размеров участка, условий местности, цены на землю и требуемой точности.
Способы вычисления площадей:
Геометрические способы используются в тех случаях, когда известны результаты измерения геометрических элементов участка – длины ее линий и величины углов или функций элементов, которыми являются координаты вершин земельного участка.
Механические способы применяются для определения площадей по топографическим планам с помощью механических приборов – планиметров, а также с помощью палеток, представляющих собой прозрачную основу с нанесенной сеткой равных по площади фигур; сторона сетки квадратов обычно составляет 2…10 мм. Палетку кладут на план и внутри контура фигуры подсчитывают число n целых квадратов и число квадратов n1, которые составлены на глаз из частей, рассеченных контуром. Площадь участка определяют по формуле :
Р=р(n-n1), р – площадь одного квадрата в масштабе плана.
Погрешность определения площади палеткой – 0,5…2,0%.
Точность измерения площадей
| Площадь Участка Р, м^3 | Значение погрешности | |||
| 1:500 | 1:1000 | 1:2000 | 1:5000 | 1:10 000 |
| 3,0 | 6,0 | 12,0 | ||
| 3,6 | 7,3 | 14,6 | ||
| 16,4 | 32,8 | 65,6 | ||
| 23,7 | 47,4 | 94,8 | ||
| 10 000 | 47,4 | 94,8 | 186,6 | 948 |
21.(6.2)
Процесс производства геодезических работ включает в себя полевые измерения, составляющие основную часть геодезических работ, и камеральную обработку измереных величин в соответствии с установленными математическими правилами и стандартами.Любую функцию измеренных величин можно назвать косвенно измеренной величиной.Для производства измерений необходимы:объект измерения ;инструменты;исполнитель;определённая естественная среда;метод измерения.С точки зрения условий их выполнения геодезические измерения разделяют на равноточные и неравноточные.
Равноточными измерениями являются однотипные результаты, которые получают при измерениях одним и тем же инструментом, одним и тем же методом.Когда нарушаются эти условия, результаты таких измерений называются неравноточными.
По классу точности результатов измерений их разделяют на высокоточные и технические.Измерения, которые необходимо выполнить, чтобы получить только по одному значению каждой искомой величины, называют необходимыми.Измерения сверх необходимых называют избыточными(не следует путать с понятием лишние!).
Виды измерений.
22. (18.1.)
Погрешность измерения Δ – это отклонение полученного результата от истинного значения измеряемой величины, которое обычно бывает неизвестно, и вопрос о составлении суждений о погрешностях измерений является одним из основных вопросов теории погрешностей измерений. Необходимо знать природу и вид возникновения погрешностей при измерениях. Источников, порождающих это явление, бывает много, и каждый из этих источников порождает часть погрешностей, которые можно назвать элементарными погрешностями.
4 основных вида элементарных погрешностей:
* изменения объекта измерения, происходящие из-за изменений, связанных только с объектами измерений;
* личные погрешности исполнителя;
* погрешности среды (внешние ошибки).
▪ погрешности по абсолютной величине не превосходят некоторого предела, зависящего от точности измерений;
▪ положительные и отрицательные погрешности, равные по абсолютной величине, встречаются в ряду примерно одинаково часто;
▪ чем больше погрешность по абсолютной величине, тем она реже встречается в ряду;
▪ среднее арифметическое значение из случайных погрешностей равноточных измерений при большом числе измерений (n) ничтожно мало, т.е. [Δ]/n
24.(20.1.)
Равноточными измерениями являются однотипные результаты, которые получают при измерениях одним и тем же инструментом или им подобным по точности прибором, одним и тем же(либо аналогичным) методом и в тех же условиях. В тех случаях, когда нарушаются эти условия, результаты таких измерений называются неравноточными.
Арифметическая середина – среднее из измеренных величин:
Х- истинное значение величины, n – количество равноточных измерений.
При неограниченном возрастании числа равноточных измерений одной и той же величины среднее арифметическое стремится к истинному значению этой величины при условии, что измерения содержат неизбежные случайные погрешности
Что такое обратная и прямая геодезическая задача: суть, методы решения, назначение
В строительстве большую часть времени занимают геодезические работы. Это комплекс различных измерений и вычислений на местности. Стоит ли говорить, что качество выполненных работ зависит от точности полученных результатов. Это влияет на размещение зданий и сооружений, а также возведение их конструктивных элементов. Все должно соответствовать проектным показателям и техническим регламентам. Геодезические работы выполняются в объеме, определенном особенностями объекта и стадией его реализации. Компания «Промтерра» специализируется на их проведении с составлением необходимых чертежей, схем и расчетов. Для этого есть все составляющие: действующая лицензия, опыт, допуск СРО, штат специалистов. Один из вопросов, который поступает при выполнении работ, касается геодезической задачи. Что это такое, как используется в работе и ее назначение.
Математика в действии
По своей сути геодезические задачи — это математика в чистом виде. Основная задача состоит в определении взаимного положения точек принадлежащих какой-либо поверхности. Наиболее часто приходится иметь дело с прямыми и обратными геодезическими задачами, но на этом математические вычисления не заканчиваются. В зависимости от поставленных условий могут применяться и другие виды. Например, решение треугольника по измеренным углам и сторонам. Интересный исторический факт: с геодезическими задачами исследователи этой темы работают уже больше трех веков, а споры относительно методов дальше продолжаются.
Что такое прямая геодезическая задача
Эта разновидность предполагает вычисление координат, то есть широты и долготы определенной точки. А она, в свою очередь, лежит на математически правильной поверхности — земном эллипсоиде. Вычисления производятся по координатам другой точки, по длине и азимуту геодезической линии. Точность решения зависит от корректности исходных данных. Для проведения вычислений используют формулы нахождения приращений и определения координат.
Специалисты применяют разные методы для получения результатов. Наиболее востребованными считаются косвенный и прямой. Они отличаются тем, что в основе лежит точность исходных данных. Косвенные методы решения очень чувствительны к ним. Если в исходнике есть значительные расстояния, изменения по азимуту, то вычисления не получится сделать, или они будут с большими погрешностями. Прямые методы работают по соотношениям сфероидической геодезии, поэтому результаты можно получить более точные. Кстати, прямой тип геодезических задач применяется при вычислении координат в теодолитном ходе.
Что такое ОГЗ: суть обратной геодезической задачи
При работе над обратной геодезической задачей вычисления проводятся по известным координатам двух точек на земном эллипсоиде. Это нужно для получения значений горизонтального положения линий между ними, а также дирекционного угла этой самой линии. В этом состоит суть. Для получения искомых величин используется вычисление румба и расстояние между координатами точек. Нужно помнить, что дирекционный угол при этом находится по четверти системы координат, которая и является объектом, где размещены искомые позиции. Для решения нужно учитывать знаки приращения, которые свойственны для определенных четвертей. В этом типе задач уделяют большое значение сходимости результатов, поэтому расчеты могут проводиться несколько раз. На это влияют свойства горизонтального положения между точками. В каких случаях применяется обратная геодезическая задача? В тех, когда по известным двум точкам и их координатам определяют расстояние не только между ними, но и дирекционный угол линии.
В том или ином виде геодезические задачи возникают и в других направлениях — в полигонометрии, триангуляции, но на этом не заканчивается востребованность. Используется также, когда стоит задача определения взаимного положения точек по исходным данным длины и направления соединяющей линии. Есть ряд случаев, когда геодезические задачи решают с использованием формул аналитической геометрии в пространстве. Речь идет о пространственных прямоугольных координатах. Для этого используют пространственные компоненты направления прямой линии между этими точками.
Обратный тип геодезической задачи — не просто математическая проверка и вычисления. Она имеет практическое значение, ведь используется при вычислении длин проектных линий. Кроме этого, используется при выполнении привязки теодолитных ходов к пунктам геодезической сети, съемочных сетей и сетей сгущения. Еще одно практическое назначение — определение направления с пункта на пункт при отсутствии видимости. Обратная геодезическая задача используется в промышленном и гражданском строительстве.
А как решать обратные задачи, если в исходнике большие расстояния? В этом случае рекомендуется использовать метод итерации. Его можно использовать при расстояниях до 20 000 км. Итерация основана на решении прямой геодезической задачи любым выбранным методом — численным или аналитическим. И точность решения именно ОГЗ определяется решением ПГЗ.
Прямые и обратные геодезические задачи требуют получения точных результатов. Насколько получится достичь поставленной цели, зависит от исходных сведений и выбранного метода решения. Вычисление способом Бесселя, методом Рунге-Кутта-Фельберга, итерации, численного интегрирования — в каждом отдельном случае выбор зависит от расстояний и координат точек. В штате компании «Промтерра» работают опытные специалисты в сфере инженерной геодезии, поэтому за решение даже самых сложных задач можно быть спокойными. Тема геодезических задач всегда остается актуальной, поэтому отслеживание последних тенденций в проведении вычислений для получения точных результатов — необходимость. Важно отметить, что подобного плана математические методы востребованы не только в геодезической сфере деятельности, но и в навигации, корректировке ракетного огня и др.
Решение обратной геодезической задачи

Координаты точекА(XA, YA) и
В(XB, YB) определяют при решении предыдущей задачи (см. п. 1.4.2).
Данная задача решается следующим образом.
Сначала находим приращения координат
Величину осевого румба rAB определяем из отношения
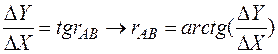
По знакам приращений координат определяем четверть, в которой располагается румб, и её название (табл. 1).
Знаки приращений координат ΔX и ΔY
| Приращения координат | Четверть окружности, в которую направлена линия | |||
| I (СВ) | II (ЮВ) | III (ЮЗ) | IV (СЗ) | |
| ΔX | + | – | – | + |
| ΔY | + | + | – | – |
Используя зависимость между дирекционными углами и осевыми румбами (рис. 11), находим aAB .
Рис. 11. Осевые румбы и дирекционные углы
Зависимость между дирекционными углами и румбами определяется для четвертей по следующим формулам:
Расстояние SAB определяем по формуле

Для контроля расстояние SAB вычисляют дважды по формулам:

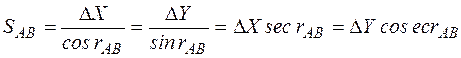
Пример.Координаты точек:А(5998.650 км, 2396.750 км);
В(6000.150 км, 2395.250 км).
Вычисляем осевой румб rAB из отношения


По знакам приращений координат ΔX > 0 и ΔY