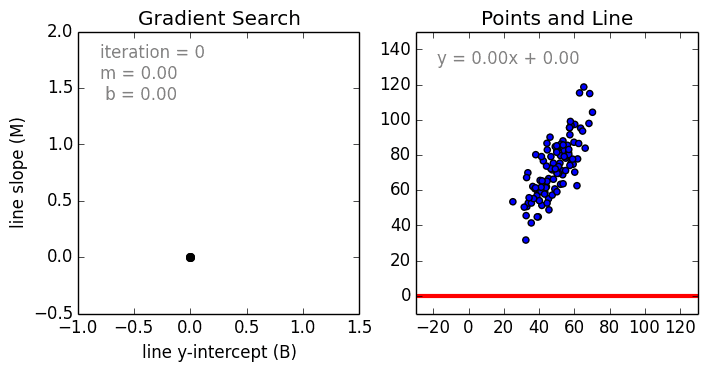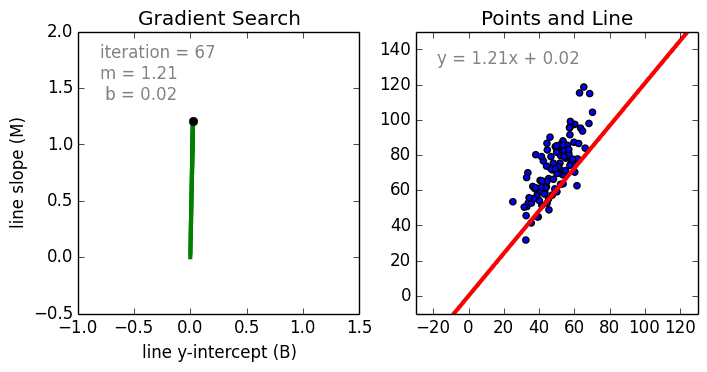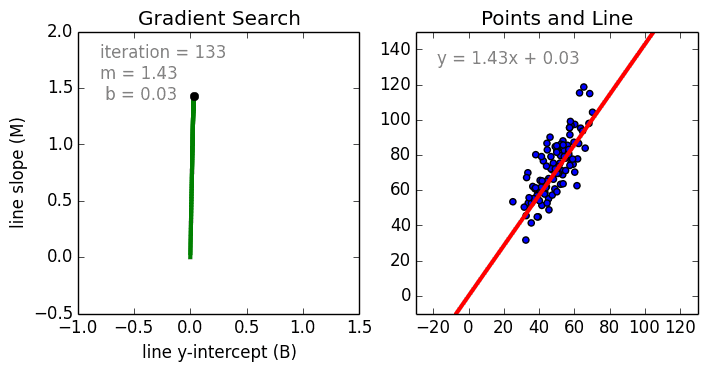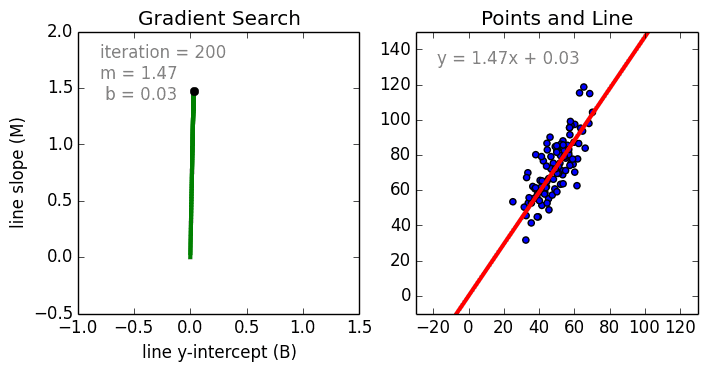
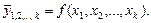какие задачи решаются при построении уравнения регрессии
Парная регрессия и корреляция
1. Парная регрессия и корреляция
1.1. Понятие регрессии
Парной регрессией называется уравнение связи двух переменных у и х
где у – зависимая переменная (результативный признак); х – независимая, объясняющая переменная (признак-фактор).
Различают линейные и нелинейные регрессии.
Линейная регрессия описывается уравнением: y = a + b × x +e .
Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Примеры регрессий, нелинейных по объясняющим переменным, но ли-
нейных по оцениваемым параметрам:
· полиномы разных степеней
· равносторонняя гипербола:
Примеры регрессий, нелинейных по оцениваемым параметрам:
· степенная
· показательная
· экспоненциальная
Наиболее часто применяются следующие модели регрессий:
– прямой
– гиперболы
– параболы
– показательной функции
– степенная функция
1.2. Построение уравнения регрессии
Постановка задачи. По имеющимся данным n наблюдений за совместным
изменением двух параметров x и y <(xi,yi), i=1,2. n> необходимо определить
аналитическую зависимость ŷ=f(x), наилучшим образом описывающую данные наблюдений.
Построение уравнения регрессии осуществляется в два этапа (предполагает решение двух задач):
– спецификация модели (определение вида аналитической зависимости
– оценка параметров выбранной модели.
1.2.1. Спецификация модели
Парная регрессия применяется, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной.
Применяется три основных метода выбора вида аналитической зависимости:
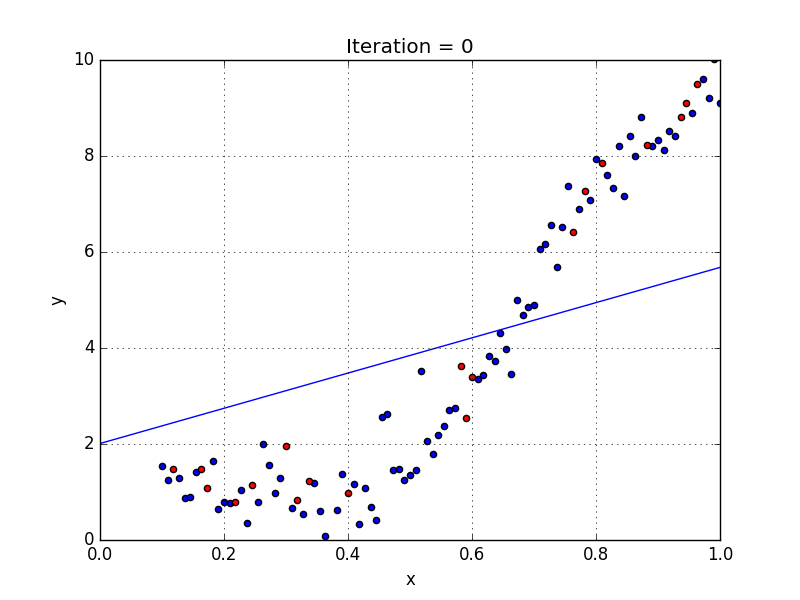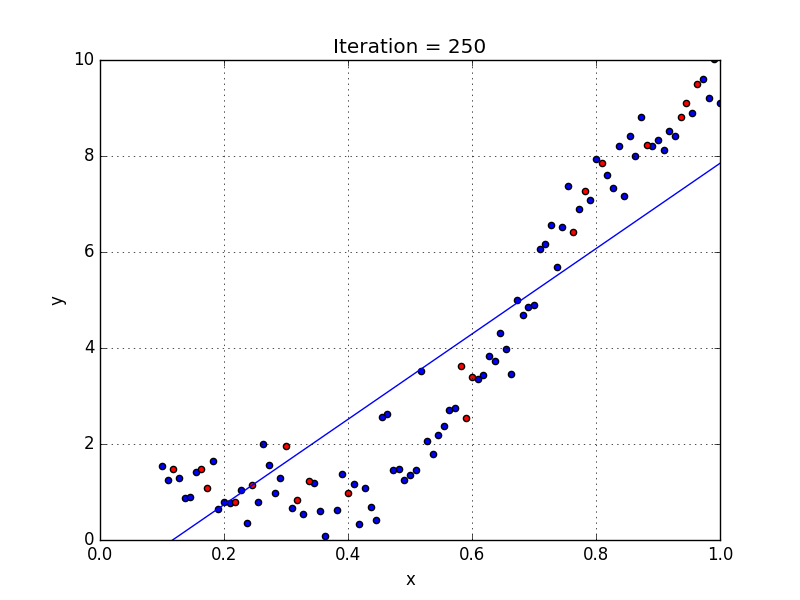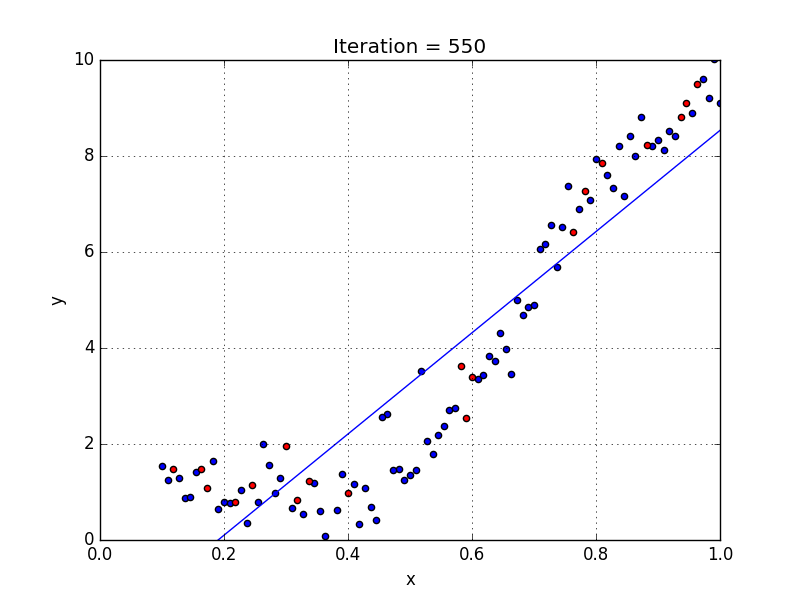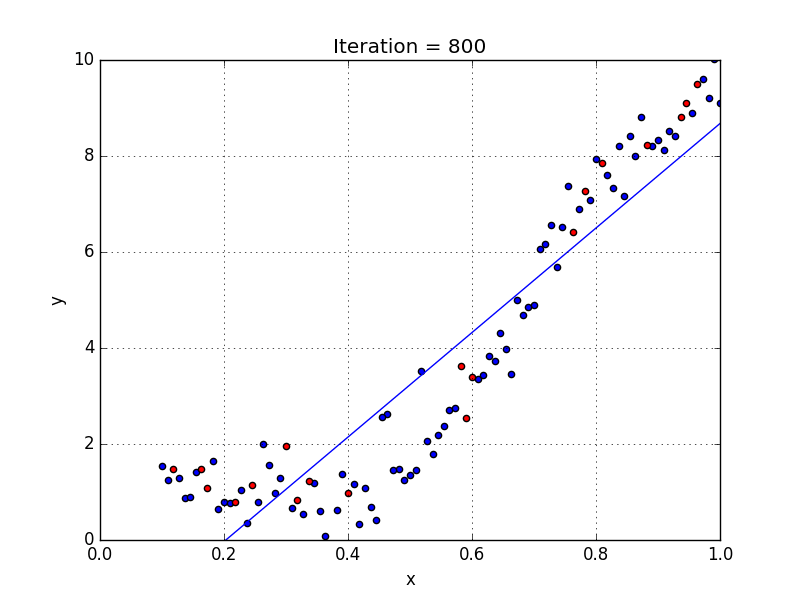
– графический (на основе анализа поля корреляций);
– аналитический, т. е. исходя из теории изучаемой взаимосвязи;
– экспериментальный, т. е. путем сравнения величины остаточной дисперсии Dост или средней ошибки аппроксимации , рассчитанных для различных
моделей регрессии (метод перебора).
1.2.2. Оценка параметров модели
Для оценки параметров регрессий, линейных по этим параметрам, используется метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических значений ŷx при тех же значениях фактора x минимальна, т. е.
В случае линейной регрессии параметры а и b находятся из следующей
системы нормальных уравнений метода МНК:

Можно воспользоваться готовыми формулами, которые вытекают из этой

Для нелинейных уравнений регрессии, приводимых к линейным с помощью преобразования (x, y) → (x’, y’), система нормальных уравнений имеет
вид (1.1) в преобразованных переменных x’, y’.
Коэффициент b при факторной переменной x имеет следующую интерпретацию: он показывает, на сколько изменится в среднем величина y при изменении фактора x на 1 единицу измерения.
Линеаризующее преобразование: x’ = 1/x; y’ = y.
Уравнения (1.1) и формулы (1.2) принимают вид
Линеаризующее преобразование: x’ = x; y’ = lny.
Модифицированная экспонента: 
Степенная функция:
Линеаризующее преобразование: x’ = ln x; y’ = ln y.
Показательная функция:
Линеаризующее преобразование: x’ = x; y’ = lny.

Линеаризующее преобразование: x’ = ln x; y’ = y.
Парабола второго порядка:
Парабола второго порядка имеет 3 параметра a0, a1, a2, которые определяются из системы трех уравнений
1.3. Оценка тесноты связи
Тесноту связи изучаемых явлений оценивает линейный коэффициент
парной корреляции rxy для линейной регрессии (–1 ≤ r xy ≤ 1)
и индекс корреляции ρxy для нелинейной регрессии

Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент детерминации r2xy (для линейной регрессии) или индекс детерминации (для нелинейной регрессии).
Коэффициент детерминации – квадрат коэффициента или индекса корреляции.
Для оценки качества построенной модели регрессии можно использовать
показатель (коэффициент, индекс) детерминации R2 либо среднюю ошибку аппроксимации.
Чем выше показатель детерминации или чем ниже средняя ошибка аппроксимации, тем лучше модель описывает исходные данные.
Средняя ошибка аппроксимации – среднее относительное отклонение
расчетных значений от фактических
Построенное уравнение регрессии считается удовлетворительным, если
значение не превышает 10–12 %.
1.4. Оценка значимости уравнения регрессии, его коэффициентов,
Оценка значимости всего уравнения регрессии в целом осуществляется с
помощью F-критерия Фишера.
F-критерий Фишера заключается в проверке гипотезы Но о статистической незначимости уравнения регрессии. Для этого выполняется сравнение
фактического Fфакт и критического (табличного) Fтабл значений F-критерия
Fфакт определяется из соотношения значений факторной и остаточной
дисперсий, рассчитанных на одну степень свободы
где n – число единиц совокупности; m – число параметров при переменных.
Для линейной регрессии m = 1 .
Для нелинейной регрессии вместо r 2 xy используется R2.
Fтабл – максимально возможное значение критерия под влиянием случайных факторов при степенях свободы k1 = m, k2 = n – m – 1 (для линейной регрессии m = 1) и уровне значимости α.
Уровень значимости α – вероятность отвергнуть правильную гипотезу
при условии, что она верна. Обычно величина α принимается равной 0,05 или
Если Fтабл Fфакт, то гипотеза Но не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
Для оценки статистической значимости коэффициентов линейной регрессии и линейного коэффициента парной корреляции применяется
t-критерий Стьюдента и рассчитываются доверительные интервалы каждого
Согласно t-критерию выдвигается гипотеза Н0 о случайной природе показателей, т. е. о незначимом их отличии от нуля. Далее рассчитываются фактические значения критерия tфакт для оцениваемых коэффициентов регрессии и коэффициента корреляции путем сопоставления их значений с величиной стандартной ошибки
Стандартные ошибки параметров линейной регрессии и коэффициента
корреляции определяются по формулам

tтабл и tфакт принимают или отвергают гипотезу Но.
tтабл – максимально возможное значение критерия под влиянием случайных факторов при данной степени свободы k = n–2 и уровне значимости α.
Связь между F-критерием Фишера (при k1 = 1; m =1) и t-критерием Стьюдента выражается равенством
Если tтабл tфакт, то гипотеза Но не отклоняется и признается случайная природа формирования а, b или 
Значимость коэффициента детерминации R2 (индекса корреляции) определяется с помощью F-критерия Фишера. Фактическое значение критерия Fфакт определяется по формуле
Fтабл определяется из таблицы при степенях свободы k1 = 1, k2 = n–2 и при
заданном уровне значимости α. Если Fтабл
Уравнение множественной регрессии



На практике изменение результативного признака y зачастую зависит от действия нескольких факторных признаков x, поэтому изучение связи между тремя признаками и более носит название множественной (многофакторной) регрессии. Аналитическое выражение связи между результативным признаком y и факторными признаками (x1, x2, …, xk) описывается функцией вида
Уравнение множественной регрессии описывает математическую зависимость результативного признака от нескольких факторных признаков.
При построении уравнения множественной регрессии необходимо решить следующие задачи:
· обосновать взаимосвязь результативного признака и факторных признаков;
· определить тип уравнения регрессии;
· количественно оценить тесноту связи между результативным признаком и факторами.
Построение моделей множественной регрессии включает три этапа:
1) выбор формы связи (уравнения регрессии);
2) отбор факторных признаков;
3) обеспечение достаточного объема совокупности.
Выбрать тип уравнения довольно сложно, так как любой форме связи могут соответствовать несколько уравнений, описывающих эти связи.
Проблема отбора факторных признаков может быть решена на основе интуитивно-логических или многомерных математико-статистических методов. Наиболее приемлемым способом отбора факторных признаков является шаговая регрессия. Она заключается в последовательном включении факторов в уравнение регрессии и последующей проверке их значимости. Если при включении нового фактора в уравнение коэффициенты регрессии меняют свои значения и знаки, а множественный коэффициент корреляции не возрастает, то данный факторный признак не рекомендуется включать в уравнение связи.
Многофакторные регрессионные модели делятся на линейные (относительно независимых переменных) и нелинейные.
Наиболее простым для построения и анализа является линейное уравнение множественной регрессии:
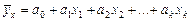
Параметры уравнения можно определить методом наименьших квадратов. Если связь между признаками является нелинейной, то выбранная для ее описания нелинейная многофакторная модель (показательная, степенная и т. д.) сводится к линейной путем линеаризации.
При использовании уравнения регрессии в решении конкретной задачи необходимо учитывать следующие условия построения уравнения регрессии:
· однородность исходных данных;
· небольшое число рассматриваемых переменных;
· отсутствие дублирующих переменных.
Для проверки достоверности уравнения регрессии применяется соотношение
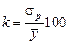
где 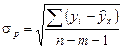
m – число факторных признаков в уравнении
регрессии.
Считается, что если значение величины k не превысит
10–15 %, то уравнение регрессии достаточно хорошо отображает изучаемую совокупность.
10.5. Показатели тесноты связи
между количественными признаками
Статистическое изучение взаимосвязей социально-экономи-
ческих явлений предполагает измерение тесноты (силы) и направления связи. Нахождение уравнения регрессии сопровождается измерением тесноты связи между признаками. Связь между количественными признаками измеряется через их вариацию. При измерении тесноты корреляционной связи ставится задача – определить, в какой мере вариация результативного признака вызвана вариацией факторного признака.
Теснота связи между количественными признаками измеряется с помощью следующих показателей:
· линейного коэффициента корреляции Пирсона rxy;
· эмпирического hэмп и теоретического корреляционного отношения hтеор;
· ранговых коэффициентов связи Спирмена (ρ) и Кендалла (τ);
· коэффициента конкордации W.
Линейный коэффициент корреляции rxy применяется для измерения тесноты парной линейной связи. При расчете коэффициента учитывается величина отклонений признаков от средних значений:
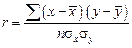
После преобразования данной формулы можно получить следующее выражение для расчета линейного коэффициента корреляции:
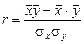
В статистике используются различные модификации формулы расчета данного коэффициента:
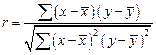
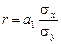
где a1 – коэффициент регрессии в уравнении связи;
sx, sy – среднее квадратическое отклонение соответствующего фак-
торного признака. Знаки коэффициентов регрессии и кор-
реляции совпадают.
Линейный коэффициент корреляции может принимать значе-
ния от –1 до +1: –1 £ r £ +1. Знак «минус» означает, что связь об-
ратная, а знак «плюс» свидетельствует о наличии прямой связи.
Интерпретация значений коэффициента корреляции представлена в табл. 10.2.
Оценка линейного коэффициента корреляцииr
Если tрасч 2 носит название коэффициента детерминации. Он показывает, в какой степени результативный признак зависит от факторного признака. Очевидно, что чем ближе коэффициент к 100 %, тем теснее выявленная зависимость между признаками.
С помощью линейного коэффициента связи r и коэффициента детерминации r 2 можно определить тесноту линейной связи между двумя признаками (табл. 10.3).
5 видов регрессии и их свойства
Jan 16, 2019 · 5 min read
Линейная и логистическая регрессии обычно являются первыми видами регрессии, которые изучают в таких областях, как машинное обучение и наука о данных. Оба метода считаются эффективными, так как их легко понять и использовать. Однако, такая простота также имеет несколько недостатков, и во многих случаях лучше выбирать другую регрессионную модель. Существует множество видов регрессии, каждый из которых имеет свои достоинства и недостатки.
Мы познакомимся с 7 наиболее распростран е нными алгоритмами регрессии и опишем их свойства. Также мы узнаем, в каких ситуация и с какими видами данных лучше использовать тот или иной алгоритм. В конце мы расскажем о некоторых инструментах для построения регрессии и поможем лучше разобраться в регрессионных моделях в целом!
Линейная регрессия
Регрессия — это метод, используемый для моделирования и анализа отношений между переменными, а также для того, чтобы увидеть, как эти переменные вместе влияют на получение определенного результата. Линейная регрессия относится к такому виду регрессионной модели, который состоит из взаимосвязанных переменных. Начнем с простого. Парная (простая) линейная регрессия — это модель, позволяющая моделировать взаимосвязь между значениями одной входной независимой и одной выходной зависимой переменными с помощью линейной модели, например, прямой.
Более распространенной моделью является множественная линейная регрессия, которая предполагает установление линейной зависимости между множеством входных независимых и одной выходной зависимой переменных. Такая модель остается линейной по той причине, что выход является линейной комбинацией входных переменных. Мы можем построить модель множественной линейной регрессии следующим образом:
Y = a_1*X_1 + a_2*X_2 + a_3*X_3 ……. a_n*X_n + b
Несколько важных пунктов о линейной регрессии:
Полиномиальная регрессия
Для создания такой модели, которая подойдет для нелинейно разделяемых данных, можно использовать полиномиальную регрессию. В данном методе проводится кривая линия, зависимая от точек плоскости. В полиномиальной регрессии степень некоторых независимых переменных превышает 1. Например, получится что-то подобное:
Y = a_1*X_1 + (a_2)²*X_2 + (a_3)⁴*X_3 ……. a_n*X_n + b
У некоторых переменных есть степень, у других — нет. Также можно выбрать определенную степень для каждой переменной, но для этого необходимы определенные знания о том, как входные данные связаны с выходными. Сравните линейную и полиномиальную регрессии ниже.
Несколько важных пунктов о полиномиальной регрессии:
Гребневая (ридж) регрессия
В случае высокой коллинеарности переменных стандартная линейная и полиномиальная регрессии становятся неэффективными. Коллинеарность — это отношение независимых переменных, близкое к линейному. Наличие высокой коллинеарности можно определить несколькими путями:
Сначала можно посмотреть на функцию оптимизации стандартной линейной регрессии для лучшего понимания того, как может помочь гребневая регрессия:
Где X — это матрица переменных, w — веса, y — достоверные данные. Гребневая регрессия — это корректирующая мера для снижения коллинеарности среди предикторных переменных в регрессионной модели. Коллинеарность — это явление, в котором одна переменная во множественной регрессионной модели может быть предсказано линейно, исходя из остальных свойств со значительной степенью точности. Таким образом, из-за высокой корреляции переменных, конечная регрессионная модель сведена к минимальным пределам приближенного значения, то есть она обладает высокой дисперсией.
Гребневая регрессия добавляет небольшой фактор квадратичного смещения для уменьшения дисперсии:
Такой фактор смещения выводит коэффициенты переменных из строгих ограничений, вводя в модель небольшое смещение, но при этом значительно снижая дисперсию.
Несколько важных пунктов о гребневой регрессии:
Регрессия по методу «лассо»
В регрессии лассо, как и в гребневой, мы добавляем условие смещения в функцию оптимизации для того, чтобы уменьшить коллинеарность и, следовательно, дисперсию модели. Но вместо квадратичного смещения, мы используем смещение абсолютного значения:
Существует несколько различий между гребневой регрессией и лассо, которые восстанавливают различия в свойствах регуляризаций L2 и L1:
Регрессия «эластичная сеть»
Эластичная сеть — это гибрид методов регрессии лассо и гребневой регрессии. Она использует как L1, так и L2 регуляризации, учитывая эффективность обоих методов.
min || Xw — y ||² + z_1|| w || + z_2|| w ||²
Практическим преимуществом использования регрессии лассо и гребневой регрессии является то, что это позволяет эластичной сети наследовать некоторую стабильность гребневой регрессии при вращении.
Несколько важных пунктов о регрессии эластичной сети:
Вывод
Вот и все! 5 распространенных видов регрессии и их свойства. Все данные методы регуляризации регрессии (лассо, гребневая и эластичной сети) хорошо функционирует при высокой размерности и мультиколлинеарности среди переменных в наборе данных.
Уравнение парной регрессии. Руководство к решению задач
Задание 1. При исследовании 8 магазинов получены следующие данные.
| Наблюдение | Объем товарооборота, млн. руб. | Число работников |
| 1 | 0,5 | 73 |
| 2 | 0,7 | 85 |
| 3 | 0,9 | 102 |
| 4 | 1,1 | 115 |
| 5 | 1,4 | 122 |
| 6 | 1,4 | 126 |
| 7 | 1,7 | 134 |
| 8 | 1,9 | 147 |
Построить регрессионную модель зависимости объема товарооборота от числа работников. Проверить значимость модели и коэффициентов модели. Рассчитать коэффициент эластичности и дать ему экономическую интерпретацию. Построить 95% доверительный интервал для оценки объема товарооборота отдельного магазина со 100 работниками.
Если вычисление каких-либо коэффициентов не запланировано заданием, соответствующие столбцы можно удалить (обычно это столбцы 9 и 10).
Автоматически строится поле корреляции.
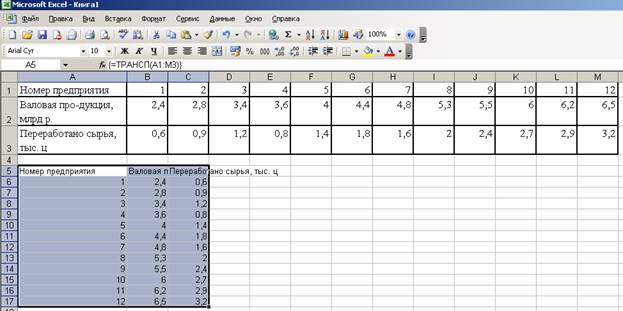
Задание 2. Имеются следующие данные о связи между произведенной продукцией (в отпускных ценах) и переработкой сырья по 12 предприятиям:
| Номер предприятия | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Валовая продукция, млрд р. | 2,4 | 2,8 | 3,4 | 3,6 | 4,0 | 4,4 | 4,8 | 5,3 | 5,5 | 6,0 | 6,2 | 6,5 |
| Переработано сырья, тыс. ц | 0,6 | 0,9 | 1,2 | 0,8 | 1,4 | 1,8 | 1,6 | 2,0 | 2,4 | 2,7 | 2,9 | 3,2 |
Составьте линейное уравнение регрессии, вычислите параметры и оцените тесноту корреляционной связи.
Видеоинструкция
Оценка тесноты корреляционной связи производится в п.1.1 отчета.
Скачать решение
Задание 3. По данным задачи 6 для изучения тесноты связи между средними товарными запасами (результативный признак Y) и оборотом розничной торговли (факторный признак) вычислите эмпирическое корреляционное отношение. Сделайте выводы.
Решение:
Эмпирическое корреляционное отношение рассчитывается в п.1.5.