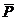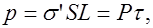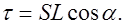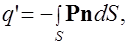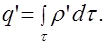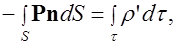какие заряды называются сторонними поляризационными

Электростатическое поле в диэлектриках. Связанные и сторонние заряды. Поляризация диэлектриков. Механизмы поляризации. Поляризационные заряды.

Диэлектрики –вещества,практически не проводящие эл. ток.

—Неполярные

—Полярные

—Ионные

Если в отсутствии внешнего электрического поля центры масс совпадают, то такие молекулы называются неполярными (неполярные диэлектрики).

Полярные молекулы обладают собственным дипольным моментом p(полярные диэлектрики).

Ионные диэлектрики представляют собой твердые неорганические диэлектрики с ионным типом химической связи.

В результате процесса поляризации в объеме (или на поверхности) диэлектрика возникают нескомпенсированные заряды, которые называются поляризационными, или связанными.

Частицы, обладающие этими зарядами, входят в состав молекул и под действием внешнего электрического поля смещаются из своих положений равновесия, не покидая молекулы, в состав которой они входят. Связанные заряды характеризуют поверхностной плотностью .

Поляризация диэлектриков — явление, связанное с ограниченным смещением связанных зарядов в диэлектрике или поворотом электрических диполей, обычно под воздействием внешнего электрического поля, иногда под действием других внешних сил или спонтанно.

Сторонние заряды –это заряды, не входящие в состав диэлектрика.

Типы поляризации:

— Электронная — смещение электронных оболочек атомов под действием внешнего электрического поля.

— Ионная — смещение узлов кристаллической решетки под действием внешнего электрического поля, причем смещение на величину, меньшую, чем величина постоянной решетки.

— Дипольная — протекает с потерями на преодоление сил связи и внутреннего трения. Связана с ориентацией диполей во внешнем электрическом поле.

Вектор поляризации — количественная мера поляризации диэлектрика, равная отношению суммарного дипольного момента физ. малого объема диэлектрика и этому объему :

Диэлектрическая восприимчивость (или поляризуемость) вещества — физическая величина, мера способности вещества поляризоваться под действием электрического поля.

где — электрическая постоянная, произведение называется в системе СИ абсолютной диэлектрической восприимчивостью.

Теорема Гаусса для поля вектора P:

Данное равенство должно выполняться для любого произвольно выбранного диэлектрика.

13. Вектор электрического смещения . Диэлектрическая проницаемость. Теорема Гаусса для поля вектора в интегральной и дифференциальной форме. Связь между и в изотропных диэлектриках.

— вектор электрического смещения или вектор индукции эл. поля или вектор

– Теорема Гаусса для поля вектора D в диф. форме —дивергенция векторного поля D в некот. точке равна объемной плотности стороннего заряда в этой точке.

Источником поля вектора D явл. только сторонние заряды.

– Теорема Гаусса для поля вектора D в инт. форме— поток вектора D индукции эл. поля через любую замкн.

поверхность (S) равен алгебраической сумме стор. зарядов, охватываемых этой поверхностью.

В случае изотропных диэлектриков:

Где диэлектрическая проницаемость в-ва.

14. Условия на границе раздела 2-х диэлектриков для векторов и . Закон преломления силовых линий. Физический смысл диэлектрической проницаемости среды.

Вблизи поверхности раздела 2-х изотропных диэлектриков при отс. сторонних зарядов поля векторов и удовлетворяют условиям:

; ; ; ;

На границе раздела 2-х диэлектриков:

— Тангенсальная составляющая:

— Нормальная составл. вектора:

Силов. линии поля векторов E,D на границе раздела 2-х сред испытывают разлом.

; ; ;

– законпреломления векторов

— модуль напряженности в диэлектрике
— модуль напряженности в вакууме
— диэлектрическая проницаемость среды

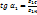
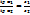
Физ. смысл : показывает, во сколько раз величина напряженности эл. поля

Источник

Свободные и связанные заряды. Поляризация вещества

Свободными зарядами называют заряды, которые под воздействием сил поля могут свободно перемещаться в веществе, их перемещение не ограничивается внутримолекулярными силами.

Под связанными зарядами принято понимать электрические заряды, входящие в состав вещества и удерживаемые в определенных положениях внутримолекулярными силами. Такие заряды «связаны» с данным веществом, неотделимы от него. Сумма положительных связанных зарядов равна сумме отрицательных связанных зарядов.

Если какое-либо диэлектрическое тело поместить в электрическое поле, то оно поляризуется.

Под поляризацией понимают упорядоченное изменение расположения связанных зарядов в теле, вызванное электрическим полем. Это изменение расположения проявляется в том, что отрицательные связанные заряды в теле переместятся в направлении более высокого потенциала, а положительные связанные заряды переместятся в сторону более низкого потенциала. Заряды сместятся настолько, что силы воздействия электрического поля на связанные заряды уравновесятся внутримолекулярными силами. В результате поляриза­ции на поверхности вещества как бы обнажаются связанные заряды.

Вектор поляризации

Электрическим моментом двух равных по величине и противоположных по знаку зарядов, находящихся друг от друга на расстоянии l (диполя), называют произведение ql. Это векторная величина, направленная от заряда -q к заряду +q (рис. 11.6, а).

Рис. 11.6. К вопросу поляризации вещества: а) – электрический диполь, б) – электрический момент суммы диполей, в) – расположение связанных зарядов в диэлектрике.

В поляризованном веществе молекулы в электрическом отношении представляют собой диполи. Под действием внешнего электрического поля диполи стремятся ориентироваться в пространстве таким образом, чтобы электрический момент их был направлен параллельно вектору напряженности электрического поля. Практический интерес представляет электрический момент не одной молекулы, не одной пары зарядов, а суммы диполей, находящихся в единице объема вещества.

Электрический момент суммы диполей, находящихся в единице объема вещества, называют вектором поляризации и обозначают буквой

. (11.12)

Для большинства диэлектриков Р пропорционален напряженности электрического поля Е. Коэффициент пропорциональности между ними обозначают обычно через k и называют электрической восприимчивостью

. (11.13)

Все диэлектрики в отношении происходящих в них процессов при поляризации могут быть разбиты на 2 группы.

В первую группу входят диэлектрики, молекулы которых при отсутствии внешнего электрического поля электрически нейтральны, т.е. в них центры действия положительных и отрицательных зарядов совпадают. К числу таких диэлектриков относятся водород, азот, парафин, слюда и др.

Поляризация в диэлектриках первой группы состоит в том, что под действием внешнего электрического поля центр действия положительного заряда молекулы сместится по внешнему полю, а центр действия отрицательных зарядов сместится против поля. В результате молекула становится диполем. Это смещение зарядов молекулы пропорционально величине напряженности внешнего поля. Смещению противодействуют внутримолекулярные силы.

Во вторую группу диэлектриков входят диэлектрики, молекулы которых при отсутствии внешнего электрического поля представляют собой диполи. Другими словами, центры действия положительных и отрицательных зарядов этих молекул при отсутствии внешнего электрического поля не совпадают (полярные молекулы). В качестве диэлектрика с полярными молекулами может быть назван, например, хлористый водород.

Благодаря тепловому движению диполи располагаются хаотично, так что при отсутствии внешнего электрического поля их электрические поля взаимно нейтрализуются. Поляризация в диэлектриках второй группы состоит в том, что полярные молекулы стремятся повернуться таким образом, чтобы их электрический момент был направлен по внешнему электрическому полю.

Источник

Поляризационные заряды

Рассмотрим, как изменяется электрическое поле в присутствии диэлектрика, и в чем состоят причины изменения. В качестве прибора для обнаружения заряда используем электрометр (см. рис. 3.2).

Рис. 3.2. При поднесении незаряженного диэлектрика

показания заряженного электрометра уменьшаются и

вновь восстанавливаются при удалении диэлектрика

Если вместо диэлектрика к электрометру приближать проводник, то наблюдается подобное явление. Здесь причиной уменьшения показаний электрометра служит электростатическая индукция – разделение электрических зарядов на проводнике в электрическом поле заряженного проводника электрометра. Значит, при внесении незаряженного диэлектрика в электрическое поле на нем также появляются заряды. Уменьшение показаний электрометра указывает на ослабление электрического поля под действием зарядов на диэлектрике. Соответственно, на ближней к заряженному проводнику электрометра стороне поверхности диэлектрика, появляются заряды противоположного знака, а на дальней – того же знака.

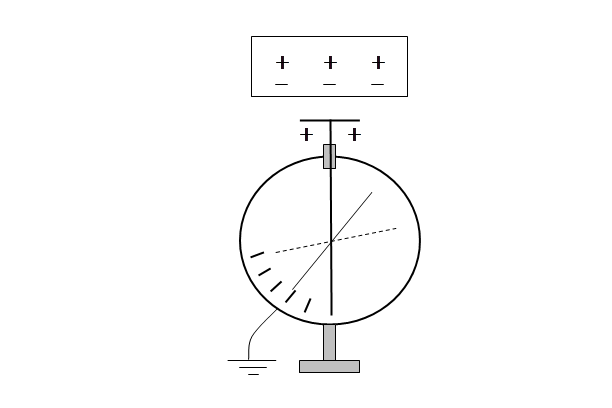
Заряды, возникающие внутри и (или) на поверхности диэлектрика при помещении его в электрическое поле называются поляризационными. Возникновение поляризационных зарядов иллюстрирует рис. 3.3.

Рис. 3.3. Модель неполяризованного (а) и

поляризованного (б) диэлектрика

При поляризации на рис. 3.3 положительные связанные заряды каждой молекулы смещаются вправо под действием поля, а отрицательные – влево. В однородном диэлектрике плотность молекул одинакова в объеме диэлектрика. Поэтому внутри объема диэлектрика положительные и отрицательные связанные заряды взаимно компенсируют друг друга. На боковых поверхностях такой компенсации нет.

Вывод:При поляризации однородного диэлектрика появляются поверхностные поляризационные заряды.

Если диэлектрик – неоднородный, то плотность молекул не постоянна в объеме диэлектрика. Поэтому в объеме диэлектрика компенсация положительных и отрицательных связанных зарядов не достигается.

Вывод:При поляризации неоднородного диэлектрика в нем появляются еще и объемные поляризационные заряды.

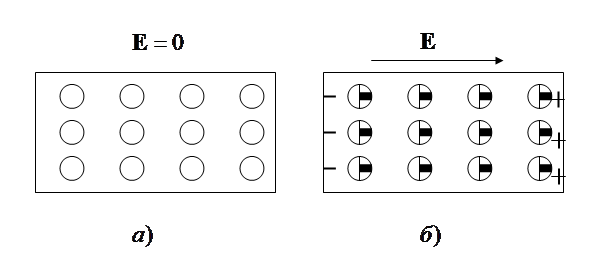
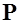
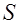
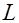
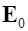
Зная поляризованность , можно найти распределение плотности поляризационных зарядов, и наоборот. Возьмем диэлектрик в виде однородной наклонной призмы с основанием и длиной , помещенной в однородное внешнее электрическое поле (см. рис. 3.4).

Рис. 3.4. К определению связи поляризованности

с поверхностной плотностью поляризационных зарядов

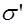
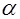
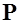
Обозначим — поверхностная плотность поляризационных зарядов, — угол между нормалью к основанию призмы и вектором . Дипольный момент призмы

Сравнивая эти выражения, получаем

(3.7)

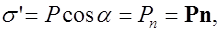
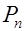
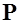
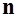
где — проекция вектора на направление единичной внешней нормали к основанию призмы.

Вывод: Поверхностная плотность поляризационных зарядов равна нормальной составляющей поляризованности в данной точке поверхности.

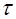
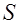
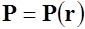
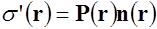
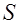
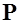
Пусть теперь диэлектрик – неоднородный. В окрестности точки наблюдения выделим объем диэлектрика, ограниченный замкнутой поверхностью . Подобно линиям напряженности поля можно ввести линии поляризованности, касательные к вектору в каждой точке. Формула (3.7) остается справедливой: , в каждой точке поверхности . При включении электрического поля связанные заряды смещаются в пределах молекул, положительные заряды – в направлении вектора , отрицательные – в противоположную сторону.

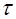
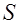
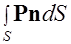
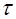
При включении электрического поля в объеме через поверхность вытекает заряд , а в объеме появится избыточный связанный заряд

который также можно выразить через плотность 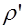связанных зарядов как

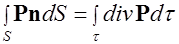
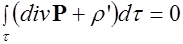
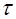
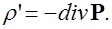
С учетом формулы Гаусса-Остроградского , далее получаем , и ввиду произвольности выбора объема найдем выражение плотности объемных связанных зарядов в неоднородном диэлектрике через вектор поляризованности:

(3.8)

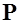
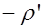
Вывод:Источниками поля поляризованности служат связанные заряды. Мощность этих источников равна . Линии поля начинаются на отрицательных связанных зарядах, а заканчиваются – на положительных.

Источник

Свободные и связанные заряды

Когда рассматриваются диэлектрики в электростатических полях, следует различать два вида электрических зарядов: свободные и связанные.

Свободные заряды – это заряды, перемещающиеся под действием поля на существенные расстояния.

Например, электроны в проводниках, ионы в газах и заряды, привносимые извне на поверхность диэлектриков, которые нарушают их (диэлектриков) нейтральность. Заряды, входящие в состав нейтральных, в целом, молекул диэлектриков, так же, как ионы, закрепленные в кристаллических решетках твердых диэлектриков около положений равновесия, получили название связанных зарядов.

Поверхностная плотность зарядов

Формула потенциала электростатического поля в диэлектрике φ запишется как:

Можно сделать вывод, что из ( 1 ) и ( 3 ) получим:

При использовании теоремы Остроградского-Гаусса с некоторыми формулами векторного анализа имеем совсем иной вид уравнения ( 4 ) :

Плотность связанных зарядов

Функция φ вида ( 7 ) будет решением уравнения:

Выражение ( 10 ) называют основным дифференциальным уравнением электростатического поля в любой произвольной среде.

Для получения полной системы уравнений электростатики, нужно использовать формулу ( 10 ) с определением, связывающим векторы напряженности электрического поля с векторами поляризации.

Зависимость P → E → представится как:

Если имеется внешнее электрическое поле, вещество становится источником поля, значит, поле изменяется.

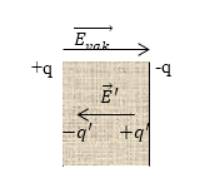
Решение

Если при имеющихся обкладках конденсатора находится вакуум, то напряженность поля, создаваемого заряженными обкладками, запишется как:

Так как известна связь напряженности поля и вектора поляризации для изотропного диэлектрика, то

На основании выше сказанного зафиксируем, что напряженность поля в конденсаторе с диэлектриком запишется как:

Источник