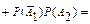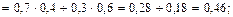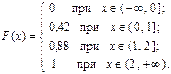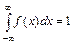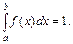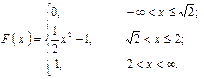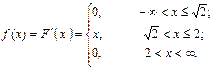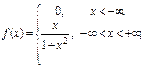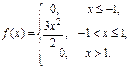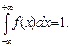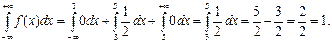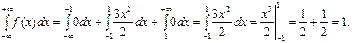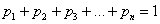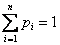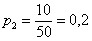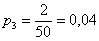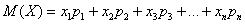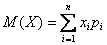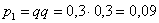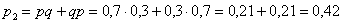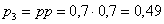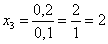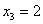какие значения может принимать функция распределения случайной величины
Какие значения может принимать функция распределения случайной величины
1. Формирование представление о случайной величине, дискретных и непрерывных случайных величинах.
2. Знакомство с законом распределения дискретной случайной величины, функцией распределения и плотностью распределения непрерывной случайной величины, числовых характеристиках случайных величин.
1. Виды случайных величин.
2. Закон распределения дискретной случайной величины.
3. Функция распределения вероятностей случайной величины.
4. Плотность распределения вероятностей непрерывной случайной величины.
5. Математическое ожидание.
6. Дисперсия и среднеквадратическое отклонение.
1. Виды случайных величин.
Случайной величиной называется такая величина, которая случайно принимает какое-то значение из множества возможных значений.
По множеству возможных значений различают дискретные и непрерывные случайные величины.
Дискретными называются случайные величины, значениями которых являются только отдельные точки числовой оси. (Число их может быть как конечно, так и бесконечно).
Пример: Число родившихся девочек среди ста новорожденных за последний месяц- это дискретная случайная величина, которая может принимать значения 1,2,3,…
Непрерывными называются случайные величины, которые могут принимать все значения из некоторого числового промежутка.
2. Закон распределения дискретной случайной величины.
Закон распределения дискретной случайной величины— это соответствие между возможными значениями случайной величины и их вероятностями.
Закон распределения можно задать таблично, аналитически, графически.
При задании закона распределения таблично, в первую строку таблицы вносятся возможные значения случайно величины, а во вторую- их вероятности.
Пример: Монету подбросили 3 раза. Запишите закон распределения числа выпадения «герба».
Возможные значения данной случайной величины: 0, 1, 2, 3.
Найдем вероятность того, что «герб» не появится (0 раз).
Найдем вероятность того, что «герб» появится 1 раз.
Найдем вероятность того, что «герб» появится 2 раза.
Найдем вероятность того, что «герб» появится 3 раза.
Тогда закон распределения данной дискретной случайной величины можно представить таблицей:
Для наглядности закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки с координатами (xi ; pi), а затем соединяют их отрезками прямых. Полученная фигура называется многоугольником распределения.
Однако, такой способ задания (перечисление всех возможных значений случайной величины и их вероятностей) не подходит для непрерывных случайных величин. Составить перечень их возможных значений невозможно.
3. Функция распределения вероятностей случайной величины.
Дадим новый способ задания любых типов случайных величин. С этой целью введем функцию распределения вероятностей случайной величины.
Функцией распределения случайной величины называют функцию F ( x ), определяющую вероятность того, что случайная величина Х в результате испытания примет значение меньшее х, т.е. F ( x ) P ( X x ).
Геометрически это равенство можно истолковать так: F ( x ) –есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.
Иногда вместо термина «функция распределения» используется термин «интегральная функция».
Свойства функции распределения:
Следствие 1: Вероятность того, что случайная величина примет значение, заключенное в интервале (а; b ), равна приращению функции распределения на этом интервале:
Пример: Случайная величина Х задана функцией распределения:
Найдите вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0; 2).
Следствие: Если возможные значения непрерывной случайной величины распределены на всей числовой оси, то справедливы следующие предельные соотношения:
Рассмотренные выше свойства позволяют представить, как выглядит график функции распределения непрерывной случайной величины.
График расположен в полосе, ограниченной прямыми у=0, у=1 (1 свойство).
4. При возрастании значения х в интервале ( a ; b ), в котором заключены все возможные значения случайной величины, график растет вверх (2 свойство).
5. При ординаты графика равны 0, при ординаты графика равны 1 (3 свойство).
Замечание: График функции распределения дискретной случайной величины имеет ступенчатый вид.
Пример: Дискретная случайная величина Х задана таблицей распределения:
Найдите функцию распределения и постройте ее график.
Итак, функция распределения имеет следующий вид:
4. Плотность распределения вероятностей непрерывной случайной величины.
Непрерывную случайную величину можно также задать, используя другую функцию, которую называют плотностью распределения или плотностью вероятности (дифференциальной функцией).
Плотность распределения вероятностей непрерывной случайной величины Х называют функцию f ( x )- первую производную от функции распределения F ( x ).
Пример: Задана плотность вероятностей случайной величины Х.
Найдите вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,5; 1).
Свойства плотности распределения вероятностей:
Свойство 1: Плотность распределения- неотрицательная функция: f ( x ) > 0.
Часто, для того чтобы характеризовать случайную величину используют числа, которые описывают случайную величину суммарно. Такие числа называются числовыми характеристиками случайной величины. К числу важнейших числовых характеристик относятся математическое ожидание и дисперсия.
5. Математическое ожидание.
Математическое ожидание приближенно равно среднему значению случайной величины. Например, если известно, что математическое ожидание числа выбиваемых очков у первого стрелка больше, чем у второго, то первый стрелок в среднем выбивает больше очков, чем второй, и следовательно стреляет лучше.
Пример: Найдите математическое ожидание, зная закон распределения дискретной случайной величины.
Какие значения может принимать функция распределения случайной величины
(F2) cХЭЕУФЧХАФ РТЕДЕМЩ Й ; (F3) ПОБ Ч МАВПК ФПЮЛЕ ОЕРТЕТЩЧОБ УМЕЧБ:
фПЮОП ФБЛ ЦЕ ДПЛБЦЕН ПУФБМШОЩЕ УЧПКУФЧБ.
(F4) ч МАВПК ФПЮЛЕ ТБЪОЙГБ ТБЧОБ :
(F5) дМС МАВПК УМХЮБКОПК ЧЕМЙЮЙОЩ ЙНЕЕФ НЕУФП ТБЧЕОУФЧП:
йЪ УЧПКУФЧ (F4) Й (F5) РПМХЮБЕН УМЕДХАЭЕЕ УЧПКУФЧП.
рПУЛПМШЛХ ЖХОЛГЙС ТБУРТЕДЕМЕОЙС ПДОПЪОБЮОП ПРТЕДЕМСЕФ ТБУРТЕДЕМЕОЙЕ УМХЮБКОПК ЧЕМЙЮЙОЩ ( ЬФХ ЖТБЪХ УФПЙФ ЛБЛ УМЕДХЕФ ПВДХНБФШ!), НПЦОП УЮЙФБФШ ЧПЪНПЦОПУФШ РТЕДУФБЧЙФШ ЖХОЛГЙА ТБУРТЕДЕМЕОЙС ЙОФЕЗТБМПН (14) ПФ ОЕПФТЙГБФЕМШОПК ЖХОЛГЙЙ ПРТЕДЕМЕОЙЕН БВУПМАФОП ОЕРТЕТЩЧОПЗП ТБУРТЕДЕМЕОЙС.
(f3) еУМЙ УМХЮБКОБС ЧЕМЙЮЙОБ ЙНЕЕФ БВУПМАФОП ОЕРТЕТЩЧОПЕ ТБУРТЕДЕМЕОЙЕ, ФП ЕЈ ЖХОЛГЙС ТБУРТЕДЕМЕОЙС ЧУАДХ ОЕРТЕТЩЧОБ.
ьФПФ ЖБЛФ УМЕДХЕФ ЙЪ УЧПКУФЧБ 7 Й ЙЪ (F4). ъБНЕФЙН, ЮФП (f3) ЕУФШ ФБЛЦЕ УМЕДУФЧЙЕ РТЕДУФБЧМЕОЙС (14) Й ОЕРТЕТЩЧОПУФЙ ЙОФЕЗТБМБ ЛБЛ ЖХОЛГЙЙ ЧЕТИОЕЗП РТЕДЕМБ.
(f4) еУМЙ УМХЮБКОБС ЧЕМЙЮЙОБ ЙНЕЕФ БВУПМАФОП ОЕРТЕТЩЧОПЕ ТБУРТЕДЕМЕОЙЕ, ФП ЕЈ ЖХОЛГЙС ТБУРТЕДЕМЕОЙС ДЙЖЖЕТЕОГЙТХЕНБ РПЮФЙ ЧУАДХ, Й
пРЙТБСУШ ОБ УЧПКУФЧБ (f4) Й (14), НПЦОП УЖПТНХМЙТПЧБФШ ФБЛПК ЛТЙФЕТЙК БВУПМАФОПК ОЕРТЕТЩЧОПУФЙ ТБУРТЕДЕМЕОЙС: ТБУРТЕДЕМЕОЙЕ У ЖХОЛГЙЕК ТБУРТЕДЕМЕОЙС БВУПМАФОП ОЕРТЕТЩЧОП, ЕУМЙ РТЙ ЧУЕИ ЙНЕЕФ НЕУФП ТБЧЕОУФЧП:
йЪ ПРТЕДЕМЕОЙС БВУПМАФОП ОЕРТЕТЩЧОПЗП ТБУРТЕДЕМЕОЙС Й УЧПКУФЧБ 7 УТБЪХ УМЕДХЕФ УЧПКУФЧП:
(f5) еУМЙ УМХЮБКОБС ЧЕМЙЮЙОБ ЙНЕЕФ БВУПМАФОП ОЕРТЕТЩЧОПЕ ТБУРТЕДЕМЕОЙЕ, ФП ДМС МАВЩИ ЙНЕАФ НЕУФП ТБЧЕОУФЧБ:
рТЙНЕТПН ФБЛПК ЖХОЛГЙЙ ТБУРТЕДЕМЕОЙС УМХЦЙФ МЕУФОЙГБ лБОФПТБ:
Функция распределения



Универсальным способом задания закона распределения, пригодным как для дискретных, так и для непрерывных случайных величин, является функция распределения.
Функцией распределения случайной величины X называется функция F(x), определяющая для каждого значения x вероятность того, что случайная величина X примет значение меньшее, чем x, то есть
Функция распределения дискретных случайных величин может быть определена по формуле
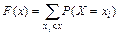
Если известен ряд распределения дискретной случайной величины, легко вычислить и построить ее функцию распределения. Продемонстрируем, как это делается на примере 23.
Пример 25. Вычислить и построить функцию распределения для дискретной случайной величины, закон распределения которой, имеет вид:
| xi | 0,1 | 1,2 | 2,3 | 4,5 |
| pi | 0,1 | 0,2 | 0,6 | 0,1 |
Решение. Определим значения функции F(x) = P(X
Из непрерывности функции F(x) следует, что вероятность каждого отдельного значения непрерывной случайной величины равна нулю.
Так как вероятность каждого отдельного значения непрерывной случайной величины равна 0, свойство 3 функции распределения для непрерывной случайной величины будет иметь вид
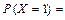
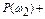
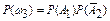
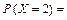
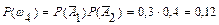
(Проверим, что 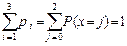
Ряд распределения данной случайной величины X имеет вид
| xi | Итого | ||
| pi | 0,42 | 0,46 | 0,12 |
Столбцовая диаграмма, соответствующая этому ряду распределения, приведена на рисунке 9.
Вычислим функцию распределения данной случайной величины:
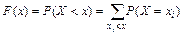
при x Î (- ¥, 0] 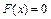
при x Î (0, 1] 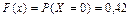
при x Î (1, 2] 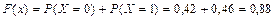
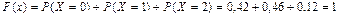
Итак, функция распределения рассматриваемой случайной величины имеет вид:
График функции F(x) приведён на рисунке 10.
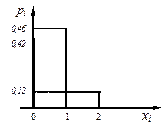 | 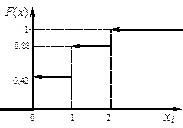 |
| Рисунок 9 – Столбцовая диаграмма | Рисунок 10 – Функция распределения |
Функция плотности распределения вероятностей непрерывной случайной величины.
Плотностью распределения вероятностей непрерывной случайной величины X в точке x называется производная ее функции распределения в этой точке:
По своему смыслу значения функции f(x) пропорциональны вероятности того, что исследуемая случайная величина примет значение где-то в непосредственной близости от точки x.
Функция плотности распределения f(x), как и функция распределения F(x), является одной из форм задания закона распределения, но она применима только для непрерывных случайных величин. Функцию плотности распределения вероятностей f(x) еще называют дифференциальной функцией распределения, тогда как функцию распределения F(x) называют, соответственно, интегральной функцией распределения.
График функции плотности распределения f(x) называется кривой распределения.
Рассмотрим свойства, которыми обладает функция плотности распределения непрерывной случайной величины.
Свойство 1. Плотность распределения вероятностей – неотрицательная функция:
(геометрически: кривая распределения лежит не ниже оси абсцисс).
Свойство 2. Вероятность попадания значения случайной величины на участок от a до b определяется по формуле
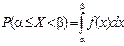
(геометрически: эта вероятность равна площади криволинейной трапеции, ограниченной кривой f(x), осью Ох и прямыми x = a и x = b).
Свойство 3.
(геометрически: площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице).
В частности, если все возможные значения случайной величины принадлежат отрезку [a, b], то
Свойство 4. Функция распределения F(x) может быть найдена по известной функции плотности распределения следующим образом:
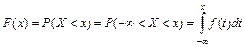
Пример 27. Непрерывная случайная величина задана функцией распределения
Определить дифференциальную функцию плотности распределения.
Решение. Определим дифференциальную функцию плотности распределения
Пример 28. Является ли плотностью распределения некоторой случайной величины каждая из следующих функций?
а) 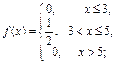
в)
Решение. а) Проверим справедливость свойства 3:
В данном случае имеем
Функция неотрицательна для всех x. То есть заданная функция является функцией плотности распределения некоторой случайной величины.
б) Заданная функция не является плотностью распределения некоторой случайной величины, так как 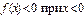
в) Проверим справедливость свойства 3:
В данном случае имеем
Функция неотрицательна для всех 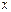
Вопросы для самоконтроля
1. Что называется случайной величиной?
2. Какие величины называются дискретными? непрерывными?
3. Что называется законом распределения случайной величины?
4. Какими способами может быть задан закон распределения дискретной случайной величины? непрерывной?
5. Что характеризует функция распределения F(x) случайной величины?
6. Как определить вероятность попадания значения случайной величины в некоторый интервал с помощью функции распределения?
7. Что характеризует функция плотности распределения случайной величины? Укажите ее вероятностный смысл.
8. Для каких величин определена функция плотности распределения?
9. Может ли функция плотности распределения принимать отрицательные значения?
10. Как связаны между собой функции F(x) и f(x)?
11. Какие случайные величины называются непрерывными?
12. Чему равна площадь фигуры, ограниченной кривой распределения и осью абсцисс?
13. Как определить вероятность попадания значения непрерывной случайной величины в некоторый интервал с помощью функции плотности распределения?
Какие значения может принимать функция распределения случайной величины
Каждая случайная величина полностью определяется своей функцией распределения.
Важно понимать, что функция распределения является “паспортом” случайной величины: она содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением.
Если функция распределения F x (x) непрерывна, то случайная величина x называется непрерывной случайной величиной.
Если функция распределения непрерывной случайной величины дифференцируема, то более наглядное представление о случайной величине дает плотность вероятности случайной величины p x (x), которая связана с функцией распределения F x (x) формулами
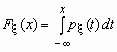
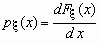
Отсюда, в частности, следует, что для любой случайной величины 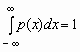
При решении практических задач часто требуется найти значение x, при котором функция распределения F x (x) случайной величины x принимает заданное значение p, т.е. требуется решить уравнение F x (x) = p. Решения такого уравнения (соответствующие значения x) в теории вероятностей называются квантилями.
Квантили, наиболее часто встречающиеся в практических задачах, имеют свои названия:
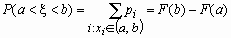
если b= 
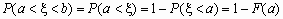
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Случайные величины. Дискретная случайная величина.
Математическое ожидание
Второй раздел по теории вероятностей посвящён случайным величинам, которые незримо сопровождали нас буквально в каждой статье по теме. И настал момент чётко сформулировать, что же это такое:
Случайной называют величину, которая в результате испытания примет одно и только одно числовое значение, зависящее от случайных факторов и заранее непредсказуемое.
Случайные величины, как правило, обозначают через 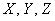
* Иногда используют 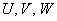
Пример встретился нам на первом же уроке по теории вероятностей, где мы фактически рассмотрели следующую случайную величину:
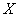
В результате данного испытания выпадет одна и только грань, какая именно – не предсказать (фокусы не рассматриваем); при этом случайная величина 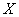
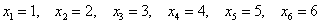
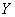
Совершенно понятно, что это количество заранее не известно, и в очередном десятке родившихся детей может оказаться:
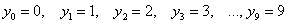
И, дабы соблюсти форму, немного физкультуры:
Её не в состоянии предугадать даже мастер спорта 🙂
Тем не менее, ваши гипотезы?
Коль скоро речь идёт о множестве действительных чисел, то случайная величина 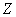
Таким образом, случайные величины целесообразно разделить на 2 большие группы:
1) Дискретная (прерывная) случайная величина – принимает отдельно взятые, изолированные значения. Количество этих значений конечно либо бесконечно, но счётно.
…нарисовались непонятные термины? Срочно повторяем основы алгебры!
2) Непрерывная случайная величина – принимает все числовые значения из некоторого конечного или бесконечного промежутка.
Примечание: в учебной литературе популярны аббревиатуры ДСВ и НСВ
Сначала разберём дискретную случайную величину, затем – непрерывную.
Закон распределения дискретной случайной величины
– это соответствие между возможными значениями этой величины и их вероятностями. Чаще всего закон записывают таблицей: 
Довольно часто встречается термин ряд распределения, но в некоторых ситуациях он звучит двусмысленно, и поэтому я буду придерживаться «закона».
А теперь очень важный момент: поскольку случайная величина 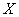
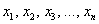
или, если записать свёрнуто:
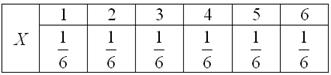
Так, например, закон распределения вероятностей выпавших на кубике очков имеет следующий вид:
Возможно, у вас сложилось впечатление, что дискретная случайная величина может принимать только «хорошие» целые значения. Развеем иллюзию – они могут быть любыми:
Некоторая игра имеет следующий закон распределения выигрыша:
Найти
…наверное, вы давно мечтали о таких задачах 🙂 Открою секрет – я тоже. В особенности после того, как завершил работу над теорией поля.
Решение: так как случайная величина 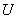
Разоблачаем «партизана»: 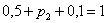
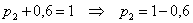
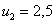
Контроль: 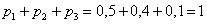
Ответ:
Не редкость, когда закон распределения требуется составить самостоятельно. Для этого используют классическое определение вероятности, теоремы умножения / сложения вероятностей событий и другие фишки тервера:
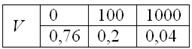
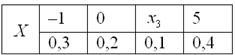
В коробке находятся 50 лотерейных билетов, среди которых 12 выигрышных, причём 2 из них выигрывают по 1000 рублей, а остальные – по 100 рублей. Составить закон распределения случайной величины 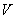
Решение: как вы заметили, значения случайной величины принято располагать в порядке их возрастания. Поэтому мы начинаем с самого маленького выигрыша, и именно 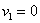
Всего таковых билетов 50 – 12 = 38, и по классическому определению:
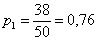
С остальными случаями всё просто. Вероятность выигрыша 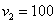
И для 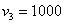
Проверка: 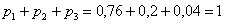
Ответ: искомый закон распределения выигрыша:
Следующее задание для самостоятельного решения:
Вероятность того, что стрелок поразит мишень, равна 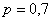
…я знал, что вы по нему соскучились 🙂 Вспоминаем теоремы умножения и сложения. Решение и ответ в конце урока.
Закон распределения полностью описывает случайную величину, однако на практике бывает полезно (а иногда и полезнее) знать лишь некоторые её числовые характеристики.
Математическое ожидание дискретной случайной величины
Говоря простым языком, это среднеожидаемое значение при многократном повторении испытаний. Пусть случайная величина 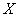
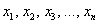
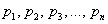
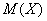
или в свёрнутом виде:
Вычислим, например, математическое ожидание случайной величины 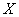
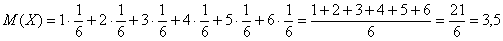
В чём состоит вероятностный смысл полученного результата? Если подбросить кубик достаточно много раз, то среднее значение выпавших очков будет близкО к 3,5 – и чем больше провести испытаний, тем ближе. Собственно, об этом эффекте я уже подробно рассказывал на уроке о статистической вероятности.
Теперь вспомним нашу гипотетическую игру:
Возникает вопрос: а выгодно ли вообще играть в эту игру? …у кого какие впечатления? Так ведь «навскидку» и не скажешь! Но на этот вопрос можно легко ответить, вычислив математическое ожидание, по сути – средневзвешенный по вероятностям выигрыш:
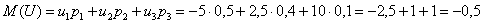
Не верь впечатлениям – верь цифрам!
Да, здесь можно выиграть 10 и даже 20-30 раз подряд, но на длинной дистанции нас ждёт неминуемое разорение. И я бы не советовал вам играть в такие игры 🙂 Ну, может, только ради развлечения.
Из всего вышесказанного следует, что математическое ожидание – это уже НЕ СЛУЧАЙНАЯ величина.
Творческое задание для самостоятельного исследования:
Мистер Х играет в европейскую рулетку по следующей системе: постоянно ставит 100 рублей на «красное». Составить закон распределения случайной величины 
Справка: европейская рулетка содержит 18 красных, 18 чёрных и 1 зелёный сектор («зеро»). В случае выпадения «красного» игроку выплачивается удвоенная ставка, в противном случае она уходит в доход казино
Существует много других систем игры в рулетку, для которых можно составить свои таблицы вероятностей. Но это тот случай, когда нам не нужны никакие законы распределения и таблицы, ибо доподлинно установлено, что математическое ожидание игрока будет точно таким же. От системы к системе меняется лишь дисперсия, о которой мы узнаем во 2-й части урока.
Но прежде будет полезно размять пальцы на клавишах калькулятора:
Случайная величина 
Найти 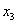
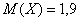
Тогда переходим к изучению дисперсии дискретной случайной величины, и по возможности, ПРЯМО СЕЙЧАС!! – чтобы не потерять нить темы.
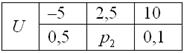
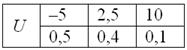
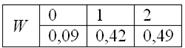
Пример 3. Решение: по условию 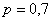
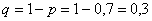
Составим 
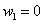
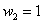
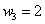
Проверка: 0,09 + 0,42 + 0,49 = 1
Ответ:
Примечание: можно было использовать обозначения 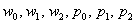
Пример 4. Решение: игрок выигрывает 100 рублей в 18 случаях из 37, и поэтому закон распределения его выигрыша имеет следующий вид: 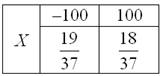
Вычислим математическое ожидание: 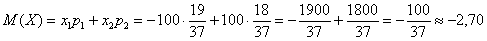
Таким образом, с каждой поставленной сотни игрок в среднем проигрывает 2,7 рубля.
Пример 5. Решение: по определению математического ожидания: 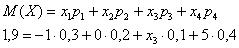
поменяем части местами и проведём упрощения: 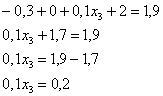
таким образом:
Выполним проверку: 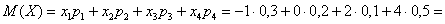
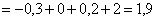
Ответ:
Автор: Емелин Александр
(Переход на главную страницу)