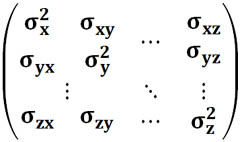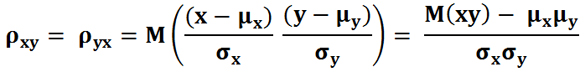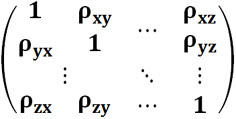какие значения может принимать ковариация случайных величин

Ковариация

которая может быть получена из первой формулы, используя свойства математического ожидания. Перечислим основные свойства ковариации.

1. Ковариация случайной величины с самой собой есть ее дисперсия.

2. Ковариация симметрична.

$$cov\left(X,\ Y\right)=cov\left(Y,\ X\right).$$

4. Постоянный множитель можно выносить за знак ковариации.

$$cov\left(cX,\ Y\right)=cov\left(X,\ cY\right)=c\cdot cov\left(X,\ Y\right).$$

5. Ковариация не изменится, если к одной из случайных величин (или двум сразу) прибавить постоянную величину:

$$cov\left(X+c,\ Y\right)=cov\left(X,\ Y+c\right)=cov\left(X+x,\ Y+c\right)=cov\left(X,\ Y\right).$$

9. Дисперсия суммы (разности) случайных величин равна сумме их дисперсий плюс (минус) удвоенная ковариация этих случайных величин:

$$D\left(X\pm Y\right)=D\left(X\right)+D\left(Y\right)\pm 2cov\left(X,\ Y\right).$$

$$M\left(X\right)=\sum^n_=-2\cdot 0,3+0\cdot 0,25+1\cdot 0,25+7\cdot 0,2=1,05.$$

$$M\left(Y\right)=\sum^n_=-6\cdot 0,25+0\cdot 0,4+3\cdot 0,35=-0,45.$$

$$M\left(XY\right)=\sum_x_iy_j>=0,1\cdot \left(-2\right)\cdot \left(-6\right)+0,2\cdot \left(-2\right)\cdot 3+0,05\cdot 1\cdot 3+0,1\cdot 7\cdot \left(-6\right)+0,1\cdot 7\cdot 3=-1,95.$$

Корреляция

Перечислим основные свойства коэффициента корреляции.

При копировании материала с сайта, обратная ссылка обязательна!

Источник

Повторение статистики для начала путешествия по науке о данных

Введение

Предположим, у нас есть диаграмма рассеяния, на которой каждая точка — это человек. На одной оси показан его профессиональный опыт в годах, на другой — доход.

В соответствии с диаграммой справа можно заключить, что между опытом и доходом нет никакой связи, то есть определенный опыт оплачивается по-разному.

Слева, наоборот, между признаками существует четкая линейная зависимость.

Ковариация и корреляция показывают, насколько тесно между собой связаны переменные набора данных.

N.B: в приведенном примере представлен двумерный вид данных (с двумя переменными). На практике статистики используют многомерные данные (со множеством переменных).

Ковариация

Ковариация — это мера зависимости между двумя или более случайных переменных.

С английского «covariance» = «co» (совместность/соединение) + «variance» (дисперсия). То есть ковариация похожа на дисперсию, но она применяется для сравнения двух переменных, где вместо суммы квадратов, мы получаем сумму векторного произведения.
Дисперсия показывает, насколько определенная переменная отличается от среднего значения, а ковариация — насколько две переменные отличаются друг от друга. Таким образом, можно утверждать следующее:

Ковариация измеряет дисперсию между двумя переменными.

Ковариация может быть отрицательной, положительной и нулевой: положительное значение показывает, что две переменные изменяются в одном направлении (если одна переменная увеличивается, то и вторая тоже увеличивается); отрицательное значение показывает, что две переменные изменяются в разных направлениях (одна увеличивается, вторая уменьшается); нулевая ковариация означает, что они изменяются независимо друг от друга.

Формула

Формулу сложно объяснить, но важно понять, что она означает:

Ковариация между переменными X и Y

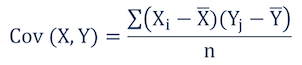
Предположим, что набор данных со случайными переменными представлен в виде вектора. Тогда в прошлом примере у нас есть два вектора для опыта и дохода. Ниже приведен порядок действий:

На втором этапе измеряется угол между двумя векторами. Если угол острый, то переменные тесно связаны между собой.

Ограниченность

Следует отметить, что несмотря на то, что ковариация измеряет зависимость между направлениями двух переменных, она не показывает тесноту этой зависимости.

На практике самая большая проблема с этой мерой заключается в том, что она зависит от используемой единицы измерения. Например, необходимо перевести годы опыта в месяцы. Тогда ковариация будет в 12 раз больше.

В этом случае на помощь приходит корреляция!

Корреляция

Корреляция — одна из наиболее распространенных мер в статистике, описывающая тесноту взаимосвязи между двумя случайными переменными. Она считается нормализованной версией ковариации. Давайте рассмотрим, почему…

Формула

Корреляция (обозначаемая греческой буквой «ро» — ρ) рассчитывается по следующей формуле:

Обратите внимание, что функциональная связь редко встречается на практике, так как две случайные переменные обычно не сопоставляются друг с другом на основе постоянного значения.

Корреляция, равная 0, означает, что между двумя переменными нет линейной зависимости. Тогда может быть отношение x = y².

Ключевые свойства

Корреляция — безразмерная величина, указывающая не только на направление взаимосвязи, но и на ее тесноту (в зависимости от того, насколько большим является абсолютное значение). Единицы измерения исключены из-за того, что ковариацию разделили на среднеквадратическое отклонение.

Напоследок необходимо запомнить, что корреляция не является причинно-следственной связью. Высокая корреляция между двумя случайными переменными просто означает, что они связаны друг с другом, но их взаимоотношение не обязательно должен иметь причинно-следственный характер. Доказать причинно-следственную связь можно только с помощью контролируемых экспериментов, при которых внешние переменные исключаются и эффекты двух данных переменных изолируются.

Источник

Ковариация случайных величин

Содержание

Вычисление [ править ]

В силу линейности математического ожидания, ковариация может быть записана как:

Свойства ковариации [ править ]

Неравенство Коши — Буняковского [ править ]

Докажем три аксиомы скалярного произведения:

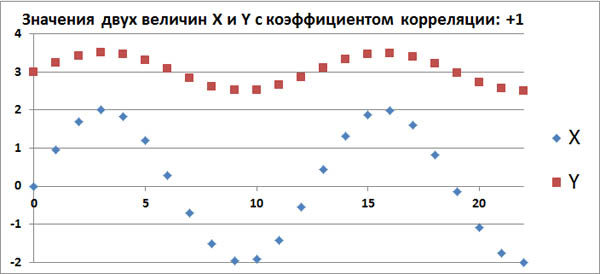
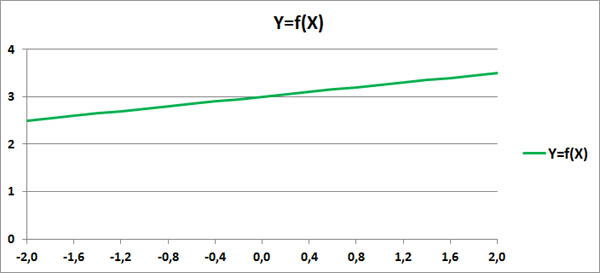
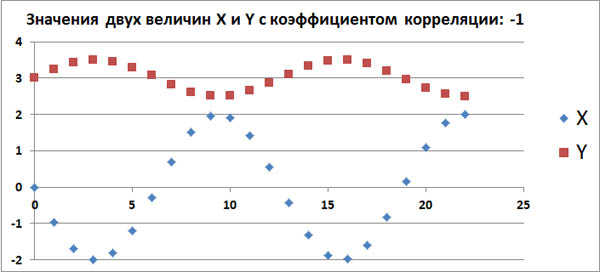
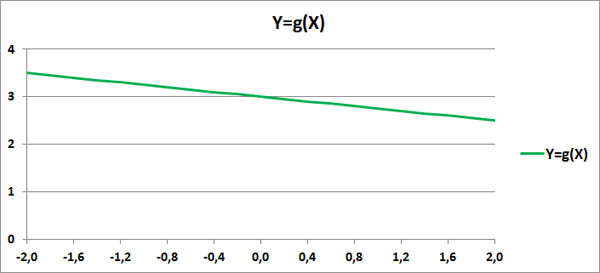
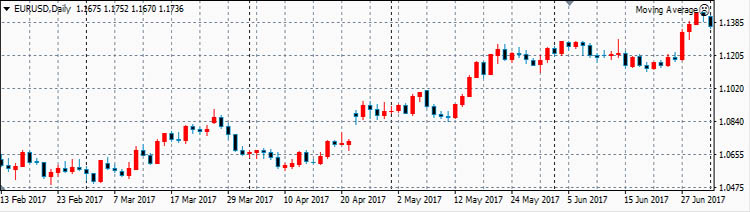
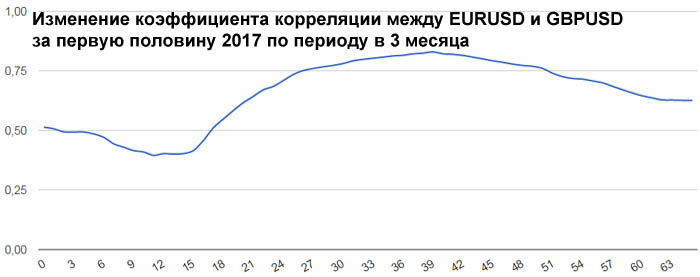
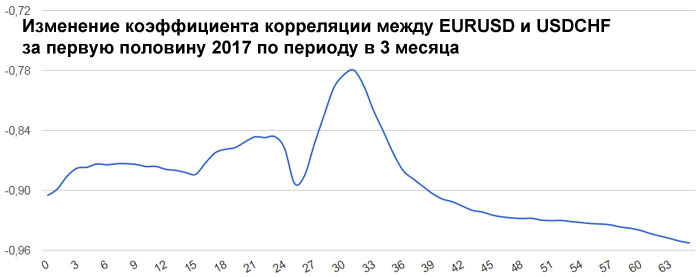
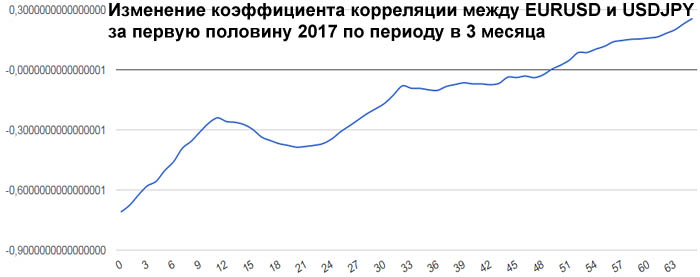
[math] \mathrm [/math] удовлетвотряет трем аксиомам, а значит [math] \mathrm [/math] можно использовать в качестве скалярного произведения.[math]\triangleleft[/math]

Для этого предположим, что [math] t [/math] — некоторое вещественное число, и рассмотрим очевидное неравенство

Используя линейность математического ожидания, мы получаем такое неравенство:

[math] E(V^2)+2 \cdot t \cdot E(V \cdot W)+t^2 \cdot E(W^2) \geqslant 0 [/math]

Итак, наш квадратный трехчлен выглядит следующим образом:

[math]\sigma_\xi ^2 \cdot t^2+2 \cdot \mathrm(\eta,\xi) \cdot t+\sigma_\eta ^2 \geqslant 0[/math]

[math] 4 \cdot \mathrm^2(\eta,\xi)-4 \cdot \sigma_\eta ^2 \cdot \sigma_\xi ^2 \leqslant 0[/math]

[math]\mathrm^2(\eta,\xi) \leqslant \sigma_\eta ^2 \cdot \sigma_\xi ^2[/math]

[math]\mathrm^2(\eta,\xi) \leqslant \mathrm[\eta] \cdot \mathrm[\xi][/math]

Матрица ковариаций [ править ]

Матрица ковариаций (англ. covariance matrix) — это матрица, элементы которой являются попарными ковариациями элементов одного или двух случайных векторов. Ковариационная матрица случайного вектора — квадратная симметрическая неотрицательно определенная матрица, на диагонали которой располагаются дисперсии компонент вектора, а внедиагональные элементы — ковариации между компонентами.

Например, ковариационная матрица для случайного вектора [math]\xi[/math] выглядит следующим образом:

Расстояние Махаланобиса [ править ]

Расстояние Махаланобиса (англ. Mahalanobis distance) — мера расстояния между векторами случайных величин, обобщающая понятие евклидова расстояния.

Расстояние Махаланобиса двух случайных векторов [math]\xi, \eta[/math] с матрицей ковариации [math]\Sigma[/math] — это мера различия между ними.

Если матрица ковариации равняется единичной матрице, то расстояние Махалонобиса равняется расстоянию Евклида.

Источник

Корреляция и Ковариация

Линейная корреляционная связь

Таких статистических связей может быть очень много самых разных. Для трейдера самым важным видом статистической связи является корреляционная связь.

Корреляционная связь, это когда каждому значению одной переменной соответствует определенное математическое ожидание другой переменной. То есть при изменении значения одной переменной, математическое ожидание другой переменной меняется закономерным образом.

А если при изменении значения одной переменной, закономерным образом меняется не только матожидание второй переменной, но и другие характеристики плотности распределения второй переменной (например, дисперсия, асимметрия и т.д.), то такая связь не является корреляционной. Хотя такая связь тоже является статистической.

Корреляционная связь между случайными переменными x и y называется линейной корреляционной связью, если матожидание переменной y линейно зависит от значений переменной x, и, одновременно, матожидание переменной x тоже линейно зависит от значений переменной y. То есть такая взаимная линейность корреляционных связей. Далее здесь рассматривается только линейная корреляционная связь.

Ковариация

Для независимых случайных величин X и Y всегда матожидание произведения случайных величин равно произведению их матожиданий по отдельности:

А для зависимых случайных величин это равенство не выполняется.

Ковариация, это отклонение математического ожидания произведения двух случайных величин от произведения их математических ожиданий:

Ковариация характеризует отклонение матожидания произведения двух случайных величин от произведения матожиданий этих величин. Так как это отклонение бывает только для зависимых величин, то ковариация характеризует степень этой зависимости. Чем она больше отличается от нуля, тем больше зависимость.

Коэффициент линейной корреляции

Ковариация неудобна тем, что имеет размерность квадрата случайных величин. Кроме того, ковариация маленькой статистической зависимости двух случайных величин с большой дисперсией (у хотя бы одной из этих величин) получается такой же, как большая статистическая зависимость у двух других случайных величин с маленькими дисперсиями. Поэтому ковариацию удобно нормировать на среднеквадратичные отклонения.

Коэффициент корреляции, это ковариация, нормированная на среднеквадратичные отклонения двух случайных величин.

Примеры

Допустим, в каком-то эксперименте в равные промежутки времени измеряют две величины, X и Y. Если их значения меняются, как на этом графике, то это полностью коррелированные величины с коэффициентом корреляции, равным +1.

Этот факт говорит о том, что между величинами X и Y имеется строгая функциональная зависимость: Y=f(X).

Этот факт также говорит о том, что между величинами X и Y имеется какая-то строгая функциональная зависимость: Y=g(X).

Теперь рассмотрим реальные цены. Для примера рассмотрим коэффициенты корреляции между ценами валютной пары EURUSD и ценами валютных пар GBPUSD, USDCHF и USDJPY. Для расчета возьмем дневные графики за первую половину 2017 года.

Эти коэффициенты корреляции достаточно ожидаемые.

Достаточно сильная корреляция между EURUSD и GBPUSD объясняется достаточно сильными связями экономики ЕвроЗоны и экономики Британии. Очень сильная антикорреляция между EURUSD и USDCHF объясняется еще более сильной связью между экономиками ЕвроЗоны и Швейцарии. А знак минус получился потому что в валютной паре USDCHF швейцарский франк стоит в знаменателе, в то время как в валютной паре EURUSD евро стоит в числителе.

Интересно посмотреть не только коэффициенты корреляции разных валютных пар, но и то, как эти коэффициенты изменяются со временем. Для этого возьмем внутри полугодового периода трехмесячный период и посмотрим, как меняется коэффициент корреляции, если сдвигать этот трехмесячный период от начала полугодового периода до его конца. Всего за полгода будет 65 таких сдвижек.

В начале 2017 года корреляция между EURUSD и GBPUSD была небольшой и она даже немного уменьшалась. Но в середине полугодия корреляция между евро и фунтом усилилась. Таким образом, в определенное время фунт может не слишком хорошо коррелировать с евро.

Источник

Ковариация и коэффициент корреляции

Ранее была рассмотрена диаграмма разброса, иллюстрирующая распределение двумерных числовых данные (см. последний раздел Изображение двумерных числовых данных заметки Представление числовых данных в виде таблиц и диаграмм). В настоящей заметке мы изучим два количественных показателя, характеризующих силу зависимости между двумя переменными — ковариацию и коэффициент корреляции. [1] Ковариация оценивает силу линейной зависимости между двумя числовыми переменными X и Y. Выборочная ковариация:

Скачать заметку в формате Word или pdf, примеры в формате Excel2013

Рассмотрим пятилетнюю среднегодовую доходность и долю затрат в фондах с очень низким уровнем риска (рис. 1). Для расчета ковариации двух выборок в Excel до 2007 года используется функция =КОВАР(), начиная с версии 2010 – функция КОВАРИВЦИЯ.В().

Рис. 1. Пятилетняя среднегодовая доходность и доля затрат взаимных фондов с очень низким уровнем риска

Любопытно, что ковариация случайной величины с собой равна дисперсии:

Если ковариация положительна, то с ростом значений одной случайной величины, значения второй имеют тенденцию возрастать, а если знак отрицательный — то убывать. Однако только по абсолютному значению ковариации нельзя судить о том, насколько сильно величины взаимосвязаны, так как её масштаб зависит от их дисперсий. Масштаб можно отнормировать, поделив значение ковариации на произведение среднеквадратических отклонений (квадратных корней из дисперсий). При этом получается так называемый коэффициент корреляции Пирсона.

Относительная сила зависимости, или связи, между двумя переменными, образующими двумерную выборку, измеряется коэффициентом корреляции, изменяющимся от –1 для идеальной обратной зависимости до +1 для идеальной прямой зависимости. Коэффициент корреляции обозначается греческой буквой ρ. Линейность корреляции означает, что все точки, изображенные на диаграмме разброса, лежат на прямой (рис 2). На панели А изображена обратная линейная зависимость между переменными X и Y. Таким образом, коэффициент корреляции ρ равен –1, т.е., когда переменная X возрастает, переменная Y убывает. На панели Б показана ситуация, в которой между переменными X и Y нет корреляции. В этом случае коэффициент корреляции ρ равен 0, и, когда переменная X возрастает, переменная Y не проявляет никакой определенной тенденции: она ни убывает, ни возрастает. На панели В изображена линейная прямая зависимость между переменными X и Y. Таким образом, коэффициент корреляции ρ равен +1, и, когда переменная X возрастает, переменная Y также возрастает.

Рис. 2. Три вида зависимости между двумя переменными

Рис. 3. Шесть диаграмм разброса и соответствующие коэффициенты корреляции, полученные с помощью программы Excel

На панели А показана ситуация, в которой выборочный коэффициент корреляции r равен –0,9. Прослеживается четко выраженная тенденция: небольшим значениям переменной X соответствуют очень большие значения переменной Y, и, наоборот, большим значениям переменной X соответствуют малые значения переменной Y. Однако данные не лежат на одной прямой, поэтому зависимость между ними нельзя назвать линейной. На панели Б приведены данные, выборочный коэффициент корреляции между которыми равен –0,6. Небольшим значениям переменной X соответствуют большие значения переменной Y. Обратите внимание на то, что зависимость между переменными X и Y нельзя назвать линейной, как на панели А, и корреляция между ними уже не так велика. Коэффициент корреляции между переменными X и Y, изображенными на панели В, равен –0,3. Прослеживается слабая тенденция, согласно которой большим значениям переменной X, в основном, соответствуют малые значения переменной Y. Панели Г–Е иллюстрируют положительную корреляцию между данными — малым значениям переменной X соответствуют большие значения переменной Y.

Обсуждая рис. 3, мы употребляли термин тенденция, поскольку между переменными X и Y нет причинно-следственных связей. Наличие корреляции не означает наличия причинно-следственных связей между переменными X и Y, т.е. изменение значения одной из переменных не обязательно приводит к изменению значения другой. Сильная корреляция может быть случайной и объясняться третьей переменной, оставшейся за рамками анализа. В таких ситуациях необходимо проводить дополнительное исследование. Таким образом, можно утверждать, что причинно-следственные связи порождают корреляцию, но корреляция не означает наличия причинно-следственных связей.

Выборочный коэффициент корреляции:

В Excel для вычисления коэффициента корреляции используется функция =КОРРЕЛ() (рис. 4).

Рис. 4. Функция КОРРЕЛ в Excel

Итак, коэффициент корреляции свидетельствует о линейной зависимости, или связи, между двумя переменными. Чем ближе коэффициент корреляции к –1 или +1, тем сильнее линейная зависимость между двумя переменными. Знак коэффициента корреляции определяет характер зависимости: прямая (+) и обратная (–). Сильная корреляция не является причинно-следственной зависимостью. Она лишь свидетельствует о наличии тенденции, характерной для данной выборки.

[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 221–227

Источник