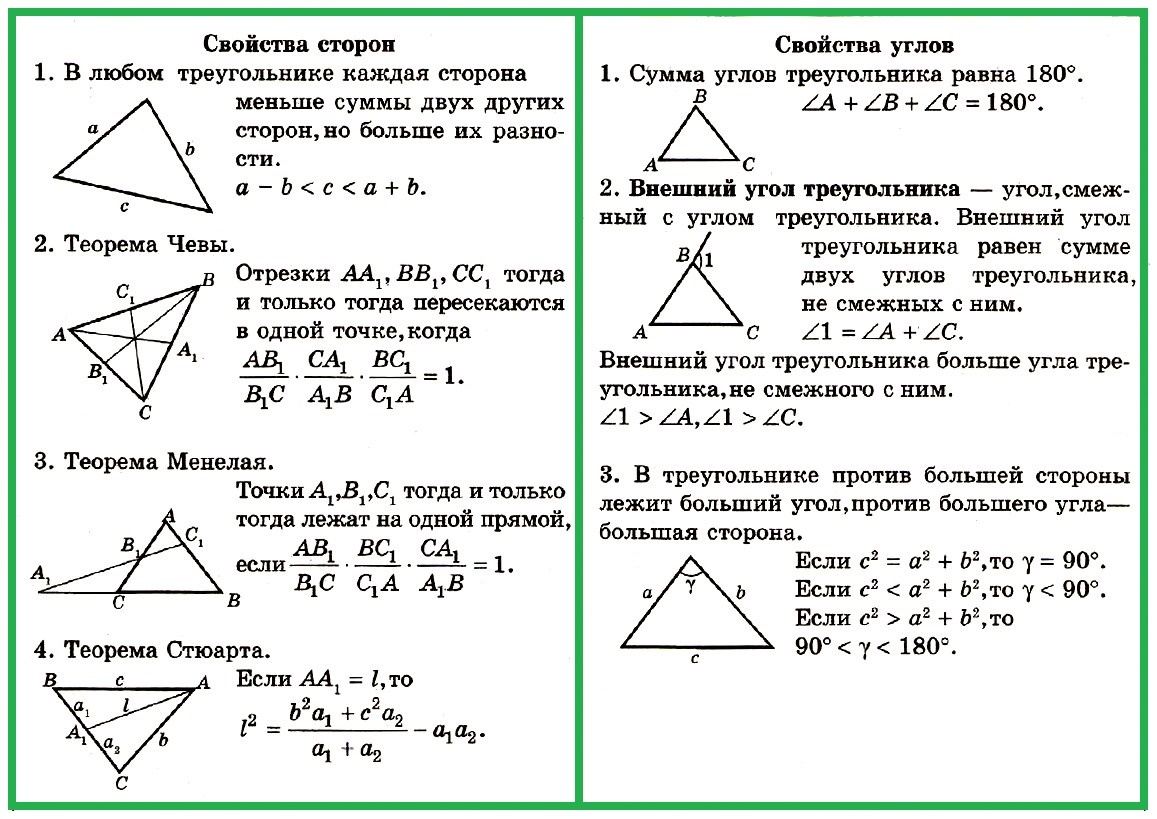
какие значения может принимать наибольший угол треугольника
Свойства сторон и углов треугольника
| Фигура | Рисунок | Формулировка |
| Треугольник |  | |
| Большая сторона треугольника |  | Против большей стороны треугольника лежит больший угол |
| Больший угол треугольника | Против большего угла треугольника лежит большая сторона | |
| Меньшая сторона треугольника |  | Против меньшей стороны треугольника лежит меньший угол |
| Меньший угол треугольника | Против меньшего угла треугольника лежит меньшая сторона | |
| Длины сторон треугольника |  | |
| Большая сторона треугольника | ||
 | Против большей стороны треугольника лежит больший угол | |
| Больший угол треугольника | ||
 | Против большего угла треугольника лежит большая сторона | |
| Меньшая сторона треугольника | ||
 | Против меньшей стороны треугольника лежит меньший угол | |
| Меньший угол треугольника | ||
 | Против меньшего угла треугольника лежит меньшая сторона | |
| Длины сторон треугольника | ||
 | ||
| Большая сторона треугольника | ||
 Свойство большей стороны треугольника: Против большей стороны треугольника лежит больший угол | ||
| Больший угол треугольника | ||
 Свойство большего угла треугольника: Против большего угла треугольника лежит большая сторона | ||
| Меньшая сторона треугольника | ||
 Свойство меньшей стороны треугольника: Против меньшей стороны треугольника лежит меньший угол | ||
| Меньший угол треугольника | ||
 Свойство меньшего угла треугольника: Против меньшего угла треугольника лежит меньшая сторона | ||
| Длины сторон треугольника | ||
 Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон. a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон. | ||
| Углы треугольника | ||
 Свойство углов треугольника: Сумма углов треугольника равна 180° Свойство внешнего угла треугольника: Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним. | ||
| Больший угол треугольника | ||
 Свойство большего угла треугольника: Величина большего угла треугольника не может быть меньшей, чем 60°.
где α – больший угол треугольника. | ||
| Меньший угол треугольника | ||
 Свойство меньшего угла треугольника: Величина меньшего угла треугольника не может быть большей, чем 60°.
где β – меньший угол треугольника. | ||
| Теорема косинусов | ||
 | ||
| Теорема синусов | ||
 Свойство меньшего угла треугольника:
Треугольник. Формулы и свойства треугольников.Типы треугольниковПо величине угловПо числу равных сторонВершины углы и стороны треугольникаСвойства углов и сторон треугольникаСумма углов треугольника равна 180°: В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы: Сумма длин двух любых сторон треугольника больше длины оставшейся стороны: a + b > c Теорема синусовСтороны треугольника пропорциональны синусам противолежащих углов. Теорема косинусовКвадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними. Теорема о проекцияхДля остроугольного треугольника: a = b cos γ + c cos β b = a cos γ + c cos α c = a cos β + b cos α Формулы для вычисления длин сторон треугольникаМедианы треугольникаСвойства медиан треугольника:В точке пересечения медианы треугольника делятся в отношении два к одному (2:1) Медиана треугольника делит треугольник на две равновеликие части Треугольник делится тремя медианами на шесть равновеликих треугольников. Формулы медиан треугольникаФормулы медиан треугольника через стороны Биссектрисы треугольникаСвойства биссектрис треугольника:Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°. Формулы биссектрис треугольникаФормулы биссектрис треугольника через стороны: Формулы биссектрис треугольника через две стороны и угол: la = 2 bc cos α 2 b + c lb = 2 ac cos β 2 a + c lc = 2 ab cos γ 2 a + b Высоты треугольникаСвойства высот треугольникаФормулы высот треугольникаha = b sin γ = c sin β hb = c sin α = a sin γ hc = a sin β = b sin α Окружность вписанная в треугольникСвойства окружности вписанной в треугольникФормулы радиуса окружности вписанной в треугольникОкружность описанная вокруг треугольникаСвойства окружности описанной вокруг треугольникаФормулы радиуса окружности описанной вокруг треугольникаR = S 2 sin α sin β sin γ R = a 2 sin α = b 2 sin β = c 2 sin γ Связь между вписанной и описанной окружностями треугольникаСредняя линия треугольникаСвойства средней линии треугольникаMN = 1 2 AC KN = 1 2 AB KM = 1 2 BC MN || AC KN || AB KM || BC Периметр треугольникаПериметр треугольника ∆ ABC равен сумме длин его сторон Формулы площади треугольникаФормула ГеронаРавенство треугольниковПризнаки равенства треугольниковПервый признак равенства треугольников — по двум сторонам и углу между нимиВторой признак равенства треугольников — по стороне и двум прилежащим угламТретий признак равенства треугольников — по трем сторонамПодобие треугольниковПризнаки подобия треугольниковПервый признак подобия треугольниковВторой признак подобия треугольниковТретий признак подобия треугольниковЛюбые нецензурные комментарии будут удалены, а их авторы занесены в черный список! Добро пожаловать на OnlineMSchool. Какие значения может принимать наибольший угол треугольникаСвойства углов ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧЗадача № 1. Дано: AB = BC, CD AB, ∠ABC = 32. Найти: ∠ACD Задача № 2. Дано: ABC, AB = BC, ∠DBC — внешний угол ABC, ∠DBC = 52. Найти: ∠BAC, ∠BCA. Задача № 3. Дано: ABC, AB = BC, ∠C = 64, AD — биссектриса ∠A. Найти: ∠ADB. Задача № 4. Дано: AD = DB, BK = KC, ∠BAD = 38, ∠BCK = 26. Найти: ∠BDK, ∠BKD, ∠DBK. Это конспект по теме «Свойства сторон и углов треугольника». Выберите дальнейшие действия: ГеометрияПлан урока: Сумма углов треугольникаРассмотрим произвольный треугольник АВС. Точки А, В и С не лежат на одной прямой, а потому через В можно провести прямую a, параллельную АС. При этом прямые СВ и АВ окажутся секущими для двух параллельных прямых: Известно, что секущие образуют пары накрест лежащие углы, причем они равны. Отметим на рисунке эти пары и обозначим их как ∠1, ∠2, ∠3 и ∠ 4. Равные углы (∠1 = ∠2, ∠3 = ∠4) отметим одним цветом. Также обозначим ∠АВС как ∠5: С одной стороны, углы 2, 4 и 5 вместе образуют развернутый угол, то есть их сумма равна 180°: В результате мы получили, что сумма углов треугольника АВС в точности равна 180°! В итоге мы можем сформулировать следующую теорему: Задание. В треуг-ке один угол равен 50°, а второй – 60°. Чему равен третий угол этого треуг-ка? Решение. Обозначим углы треугольника как ∠1, ∠2 и ∠3. Получили обыкновенное уравнение с одной переменной. Для его решения просто перенесем слагаемые 50° и 60° из левой части в правую: Задание. Докажите, что у любого треуг-ка есть хотя бы один угол, который не превосходит 60°. Решение. Докажем это утверждение методом «от противного». Пусть существует такой треуг-к, у которого каждый из углов больше 60°. Это можно записать в виде трех неравенств: В итоге имеем, что в сумме эти углы больше 180°, а это невозможно. Это противоречие, следовательно, треуг-к с тремя углами, каждый из которых больше 60°, не существует. Задание. Основанием рав-бедр. ∆АВС является сторона АС. Известно, что ∠В = 40°. Чему равны ∠А и ∠С этого треуг-ка? Решение. Сначала необходимо вспомнить важное свойство – углы равнобедренного треугольника при его основании равны друг другу. В нашем случае это значит, что ∠А = ∠С: Задание. Один из углов при основании рав-бедр. треуг-ка равен 50°. Найдите два других угла. Решение. Построим рисунок по условию задачи: Отдельного внимания заслуживает равносторонний треуг-к. Напомним, что у него равны все три стороны. Построим его: Теперь подумаем о том, чему равны его углы. С одной стороны, мы можем рассматривать ∆АВС как рав-бедр. с основанием АС, ведь AB = BC. Тогда∠А = ∠С. Но с другой стороны, всё тот же ∆АВС мы можем одновременно считать и рав-бедр. с основанием АВ, ведь АС = ВС. Из этого следует, что ∠А = ∠С. В итоге получаем, что все три угла ∆АВС равны: Итак, получили удивительный факт – в равностороннем треуг-ке все углы равны 60°! Рассмотрим чуть более сложную задачу, где неизвестен ни один из углов треуг-ка, однако известны некоторые соотношения между ними. Задание. Первый угол треуг-ка больше второго в 2 раза, а третий равен сумме первых двух углов. Чему равны углы треуг-ка? Решение. Для большей наглядности примем первый угол треуг-ка за неизвестную величину, то есть за х. Тогда второй угол будет равен 2х, а третий окажется равным их сумме: Внешние углы треугольникаПостроим некоторый треуг-к, а потом продлим одну из его сторон. На рисунке мы продлили сторону АС. В результате образуется угол, который называют внешним углом треугольника: На рисунке видно, что ∠ВСD является внешним. Но одновременно можно утверждать и ещё один факт – углы ∠АСВ и ∠ВСD являются смежными. Это позволяет нам дать следующее определение: В итоге мы доказали, что внешний угол треугольника равен сумме двух углов треуг-ка, которые с ним не смежны. Задание. У ∆АВС ∠А = 50°, ∠В = 75°. Найдите величину внешнего угла, смежного с ∠С. Решение. В данном случае, согласно доказанному нами правилу, достаточно просто сложить ∠А и ∠B: Рассмотрим ещё несколько более тяжелых задач. Задание. В ∆АВС проведены биссектрисы угловА и B. Они пересекаются в точке М. Известно, что ∠А = 58°, ∠B = 96°. Найдите ∠АМB. Решение. Устно такую задачу не решить, поэтому построим рисунок: АМ – это биссектриса, а она разбивает∠ВАС на два равных угла. Поэтому мы можем вычислить ∠ВАМ: Отметим найденные углы на рисунке: Обратите внимание на ∆АВМ, который выделен красным цветом. Теперь мы знаем два угла в нем. Значит, можно найти и третий! Запишем для ∆АВМ сумму его углов: Задание. Построен внешний угол равнобедренного треугольника, который смежен с вершиной, лежащей против основания. Далее построили биссектрису этого внешнего угла. Докажите, что эта биссектриса будет параллельна основанию. Решение. Выполним построение: Пусть АС – это основание рав-бедр. ∆АВС. Тогда внешний угол должен быть проведен к вершине В, ведь именно она лежит против основания. Обозначим внешний угол как ∠СВD (для этого мы просто добавили точку Dна продолжение отрезка АВ). Далее проводим биссектрису ВК. Нам требуется доказать, что ВК||АС. Поступим очень просто – обозначим неизвестную нам величину угла при основании как х. То есть В результате мы получили, что и ∠С, и ∠CBK равны х, то есть они равны и друг другу. Однако эти углы являются накрест лежащими для прямых АС и ВК и секущей ВС. Из равенства накрест лежащих углов следует, что АС||ВК. Задание. В ∆АВС проведена медиана АМ, причем ее длина равна ВМ. Найдите ∠А. Решение. Напомним, что медиана – это прямая, разбивающая сторону на два равных отрезка. То есть ВМ = МС. По условию АМ = ВМ, значит, имеет место двойное равенство: Посмотрите на рисунок – здесь есть сразу два рав-бедр. треуг-ка! Это ∆АВМ (с основанием АВ) и ∆АМС (с основанием АМС). Обозначим∠В как х, а ∠С – как у. Углы при основании рав-бедр. треуг-ков одинаковы, а потому Сравнение сторон и углов треугольникаДокажем следующую теорему: Построим ∆АВС, в котором сторона АВ будет длиннее, чем АС. Нам надо доказать, что ∠С >∠B: Выполним дополнительное построение – отметим на прямой АВ такую точку D, что AD = АС. Точка D будет располагаться на отрезке АВ, ведь АВ больше АС, а, значит, и больше АD. Также соединим C и D отрезком: Теперь рассмотрим ∆ADC. Он является рав-бедр., ведь AD = AC. Из этого следует, что ∠ADC = ∠ACD. Можно заметить, что ∠АDС является внешним углом для ∆BDC. Это значит, что Мы доказали только первую часть теоремы. Теперь надо доказать обратное утверждение – против большего угла находится большая сторона треугольника. Предположим обратное, что существует ∆АВС, в котором ∠С>∠B, но не выполняется условие АВ >AC. Тогда либо АВ = ВС, либо АВ AC. Задание. В ∆АВС известны углы: Запишите стороны этого треуг-ка в порядке возрастания. Решение. Всё очень просто – чем больше сторона, тем против большего угла она лежит. Поэтому самая большая сторона – это АВ, вторая по длине – АС, а наименьшая сторона – ВС. То есть BС Доказанная теорема помогает сформулировать важный признак рав-бедр. треуг-ка: Действительно, против равных углов должны лежать равные стороны, в противном случае сложится ситуация, когда в треуг-ке против сторон разной длины будут лежать равные углы, что невозможно. Задание. В рав-бедр. ∆АВС основанием является АС. Из точек А и С проведены биссектрисы, которые пересеклись в точке О. Докажите, что ∆АОС также является рав-бедр. Ясно, что ∠ВАС = ∠ВСА, так как это углы при основании рав-бедр. ∆АВС. С другой стороны, ∠ОАС равен половине ∠ВАС, ведь АО – биссектриса: В итоге имеем, что ∠ОАС и ∠АСО равны. Но тогда в ∆АОС есть два одинаковых угла, а потому он является рав-бедр. (АО = ОС). Неравенство треугольникаСледующая важная теорема называется неравенством треугольника: Попробуем доказать неравенство треугольника. Возьмем произвольный ∆АВС и покажем, что сторона АВ меньше, чем величина ВС + АС. Для этого «дорисуем» к отрезку АС ещё один отрезок СD, равный BC, при этом АС и СD должны лежать на одной прямой: Так как AD = АС + СD, то нам достаточно показать, что АВ Получается, что в ∆АВD сторона АВ лежит против меньшего угла по сравнению со стороной АD. Значит, эта сторона должна быть меньше АD, что мы и пытаемся доказать. Доказанная теорема означает, что не всякий треуг-к можно построить по его сторонам. Так, у нас никогда не получится построить треуг-к, у которого стороны равны 2, 3 и 7 см, так как одна из этих длин больше, чем сумма двух других: Верно обратное утверждение – если все заданные длины удовлетворяют неравенству, то треуг-к построить можно. Задание. Известны две стороны равнобедренного треугольника, они равны 25 и 10 см. Какая из них является основанием? Решение. Рассмотрим сперва случай, когда основание равно 25 см. Тогда две другие стороны имеют длину 10 см. Их сумма (10 см + 10 см = 20 см) меньше основания. Такая ситуация невозможно из-за неравенства треуг-ка. Ситуация же, при которой основание имеет длину 10 см, вполне допустима. Тогда две другие стороны равны 25 см, и для каждой стороны неравенство треуг-ка выполняется: Какие значения может принимать наибольший угол треугольникаКакие из следующих утверждений верны? 1) В треугольнике ABC, для которого 2) В треугольнике ABC, для которого AB = 4, BC = 5, AC = 6, угол B — наибольший. 3) Внешний угол треугольника больше каждого внутреннего угла. 4) Треугольник со сторонами 1, 2, 3 не существует. Проверим каждое из утверждений. 1) «В треугольнике ABC, для которого 2) « В треугольнике ABC, для которого AB = 4, BC = 5, AC = 6, угол 3) «Внешний угол треугольника больше каждого внутреннего угла.» — неверно, внешний угол треугольника может быть больше внутреннего угла треугольника, например в случае тупоугольного треугольника. 4) «Треугольник со сторонами 1, 2, 3 не существует.» — верно, не каждая сторона треугольника меньше суммы двух других сторон.
| ||
 ,
, ,
, ,
,