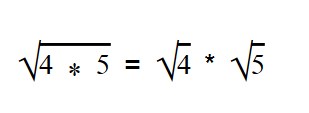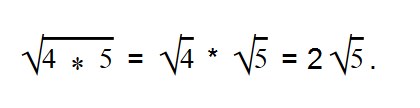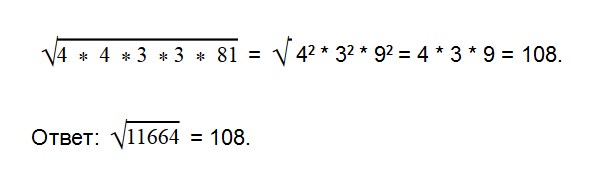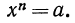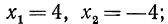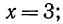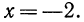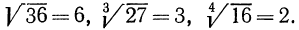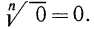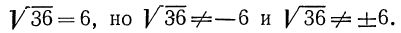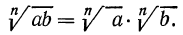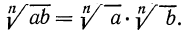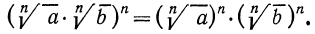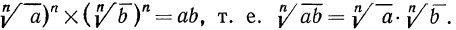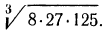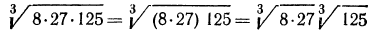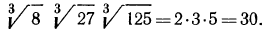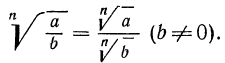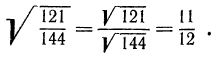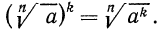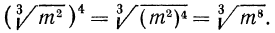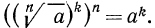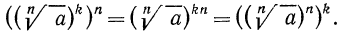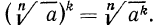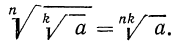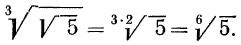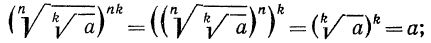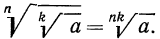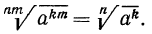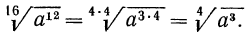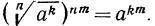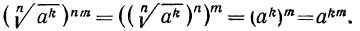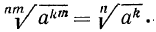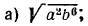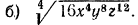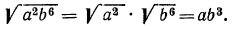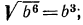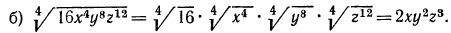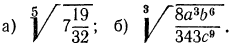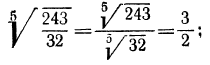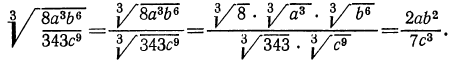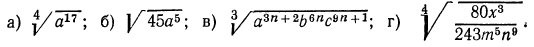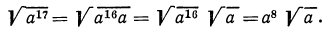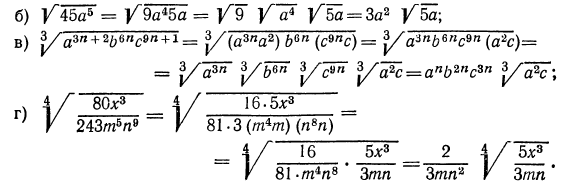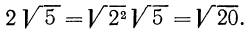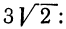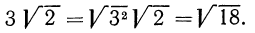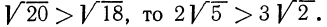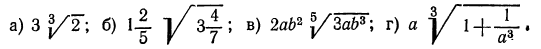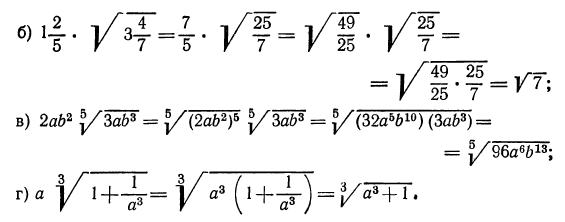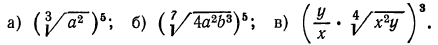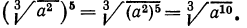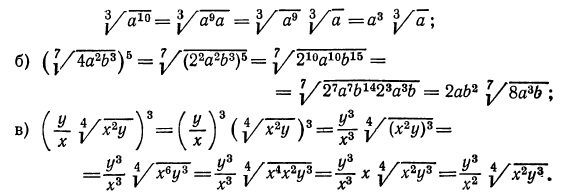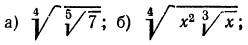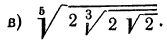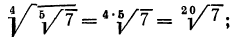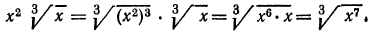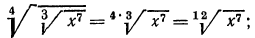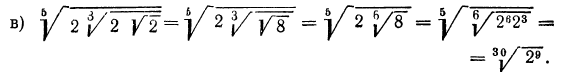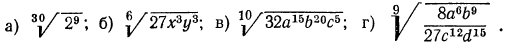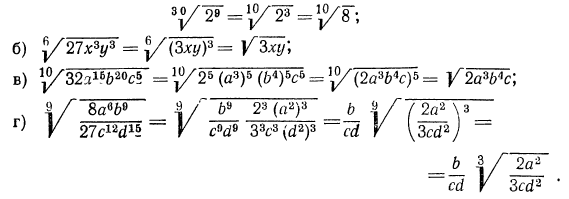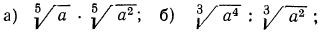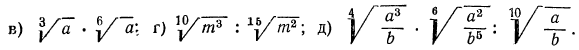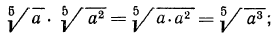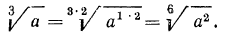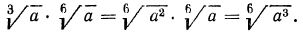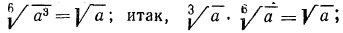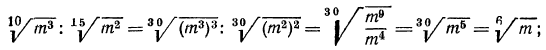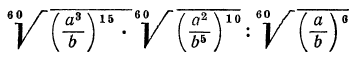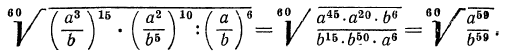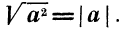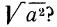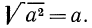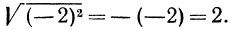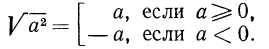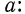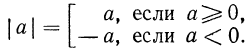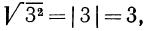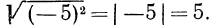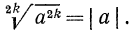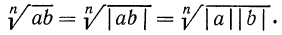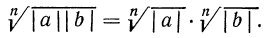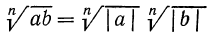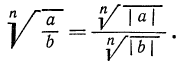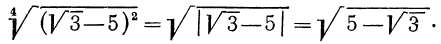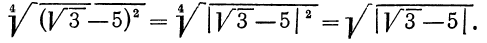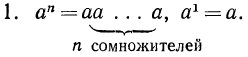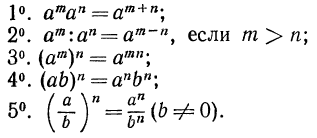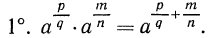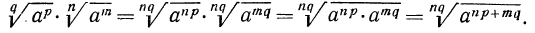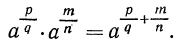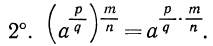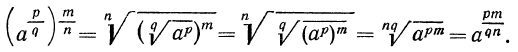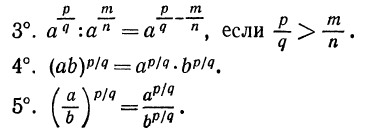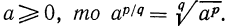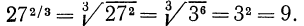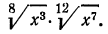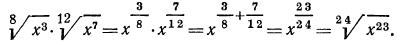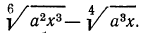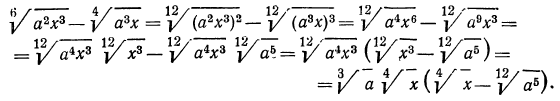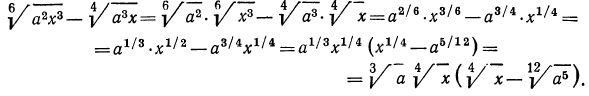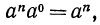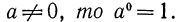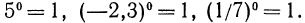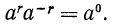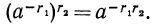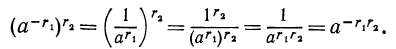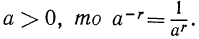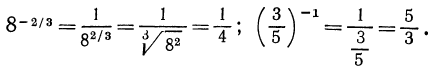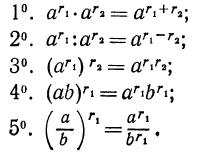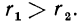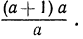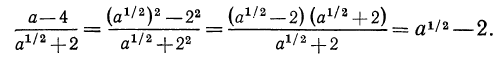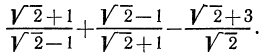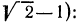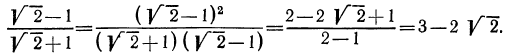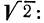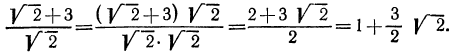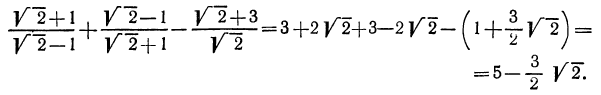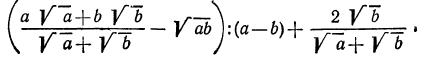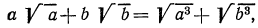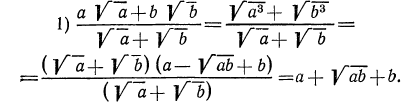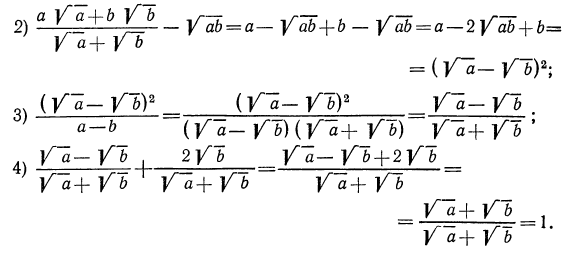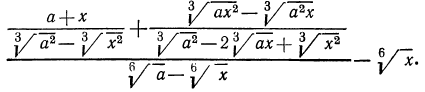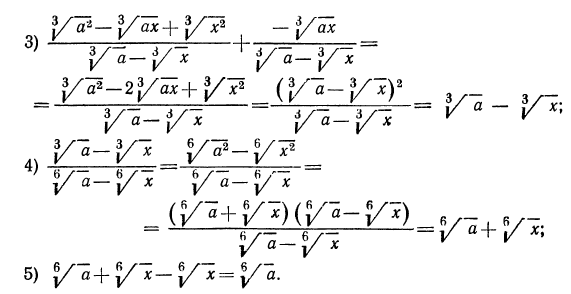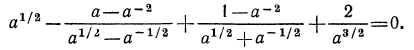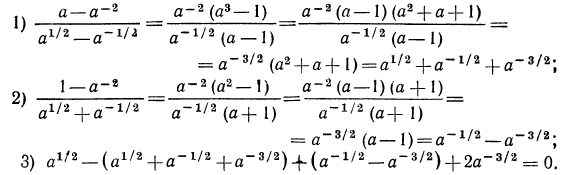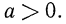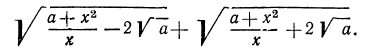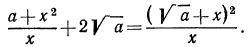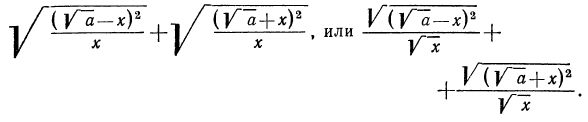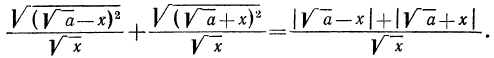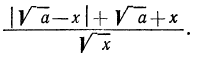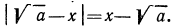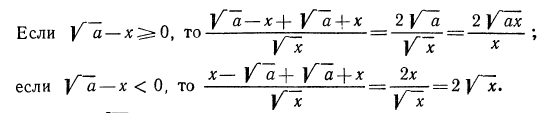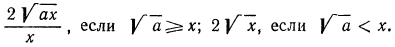какие значения может принимать подкоренное выражение

Что такое квадратный корень

Что такое квадратный корень

Определение арифметического квадратного корня ясности не добавляет, но заучить его стоит:

Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a.

Определение квадратного корня также можно представить в виде формул:
√a = x
x 2 = a
x ≥ 0
a ≥ 0

Из определения следует, что a не может быть отрицательным числом. То есть то, что стоит под корнем — обязательно положительное число.

Чтобы разобраться, почему именно так и никак иначе, давайте рассмотрим пример.

Попробуем найти корень из √-16

Здесь логично предположить, что 4, но давайте проверим: 4*4 = 16 — не сходится.

Получается, что ни одно число не может дать отрицательный результат при возведении его в квадрат.

Числа, стоящие под знаком корня, должны быть положительными.

Исходя из определения, значение корня также не должно быть отрицательным.

Разница между квадратным корнем и арифметическим квадратным уравнением

Прежде всего, чтобы разграничить эти два понятия, запомните:

Это два нетождественных друг другу выражения.

Из выражения x 2 = 16 следует, что:

Если две вертикальные палочки возле x вводят вас в замешательство, почитайте нашу статью о модуле числа.

В то же самое время, из выражения x = √16 следует, что x = 4.

Если ситуация все еще кажется запутанной и нелогичной, просто запомните, что отрицательное число может быть решением только в квадратном уравнении. Если в решении «минус» — есть два варианта:

Если вы извлекаете квадратный корень из числа, то можете быть уверены, вас ждет «положительный» результат.

Давайте рассмотрим пример, чтобы окончательно выяснить разницу между квадратным корнем и квадратным уравнением.

Даны два выражения:

Первое выражение — квадратное уравнение.

Второе выражение — арифметический квадратный корень.

Мы видим, что результатом решения первого выражения стали два числа — отрицательное и положительное. А во втором случае — только положительное.

Запись иррациональных чисел с помощью квадратного корня

Иррациональное число — это число, которое нельзя представить в виде обыкновенной дроби.

Чаще всего, иррациональные числа можно встретить в виде корней, логарифмов, степеней и т.д.

Примеры иррациональных чисел:

Чтобы упростить запись иррациональных чисел, математики ввели понятие квадратного корня. Давайте разберем пару примеров, чтобы увидеть квадратный корень в деле.

Дано уравнение: x 2 = 2.

Сразу сталкиваемся с проблемой, поскольку очевидно, что ни одно целое число не подходит.

Переберем числа, чтобы удостовериться в этом:

1 * 1 = 1,
2 * 2 = 4,
3 * 3 = 9.

Отрицательные числа дают такой же результат. Значит результатом решения не могут быть целые числа.

Извлечение корней

Решать примеры с квадратными корнями намного легче, если запомнить как можно больше квадратов чисел. Для этого воспользуйтесь таблицей — сохраните ее себе и используйте для решения задачек.

Таблица квадратов

Вот несколько примеров извлечения корней, чтобы научиться пользоваться таблицей:

Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.

Ищем в таблице число 3025.
Влево — 5, вверх — 5.

Ищем в таблице число 7396.

Ищем в таблице число 9025.

Ищем в таблице число 1600.

Извлечением корня называется нахождение его значение.

Свойства арифметического квадратного корня

У арифметического квадратного корня есть 3 свойства — их нужно запомнить, чтобы проще решать примеры.

Давайте потренируемся и порешаем примеры на все три операции с корнями. Не забывайте обращаться к таблице квадратов. Попробуйте решить примеры самостоятельно, а для проверки обращайтесь к ответам.

Умножение арифметических корней

Для умножения арифметических корней используйте формулу:

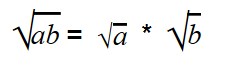Примеры:

Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.

Если нет возможности извлечь корни из чисел, то поступаем так:

Деление арифметических корней

Для деления арифметических корней используйте формулу:

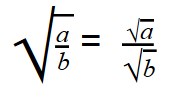Примеры:

Выполняя деление, не забывайте сокращать множители. При делении арифметических корней, используйте правила преобразования обыкновенных дробей.

Возведение арифметических корней в степень

Для возведения арифметического корня в степень используйте формулу:

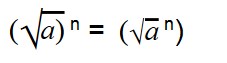Примеры:

Эти две формулы нужно запомнить:

Повторите свойства степеней, чтобы без труда решать такие примеры.

Внесение множителя под знак корня

Вы уже умеете по-всякому крутить и вертеть квадратными корнями: умножать, делить, возводить в степень. Богатый арсенал, не правда ли? Осталось овладеть еще парой приемов и можно без страха браться за любую задачку.

А теперь давайте разберемся, как вносить множитель под знак корня.

Число семь умножено на квадратный корень из числа девять.

Извлечем квадратный корень и умножим его на 7.

В данном выражение число 7 — множитель. Давайте внесем его под знак корня.

Запомните, что вносить множитель под знак корня обязательно нужно так, чтобы значение исходного выражения осталось неизменным. Иными словами, после наших манипуляций с корнем, значение выражения должно по-прежнему оставаться 21.

Вы помните, что (√a) 2 = a

Тогда число 7 должно быть возведено во вторую степень. В этом случае значение выражения останется тем же.

7√9 = √7 2 * 9 = √49 * 9 = √49 * √9 = 7 * 3 = 21.

Формула внесения множителя под знак корня:

Потренируемся вносить множители. Попробуйте решить примеры самостоятельно, сверяясь с ответами.

Вынесение множителя из-под знака корня

С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.

Дано выражение в виде квадратного корня из произведения.

Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.

Извлекаем корень из всех имеющихся множителей.

В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:

Таким образом множитель выносится из-под знака корня.

Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.

Раскладываем подкоренное выражение на множители 28 = 7*4.

Сравнение квадратных корней

Мы почти досконально разобрали арифметический квадратный корень, научились умножать, делить и возводить его в степень. Теперь вы без труда можете вносить множители под знак корня и выносить их оттуда. Осталось научиться сравнивать корни и стать непобедимым теоретиком.

Итак, чтобы понять, как сравнить два квадратных корня, нужно запомнить пару правил.

Если:

Потренируйтесь в сравнении корней. Сверяете свои результаты с ответами.

Ответ: преобразовываем выражение 9√5.

9√5 = √81 * √5 = √81*5 = √405

Ответ: преобразовываем выражение 7√12.

7√12 = √49 * √12 = √49*12 = √588

Это значит, что 7√12 > √20.

Как видите, ничего сложного в сравнении арифметических квадратных корней нет.

Самое главное — выучить формулы и сверяться с таблицей квадратов, если значения корня слишком большие для легкого вычисления в уме.

Не бойтесь пользоваться вспомогательными материалами. Математика просто создана для того, чтобы окружить себя подсказками и намеками.

Когда вы почувствуете, что уже достаточно натренировались в решении примеров с квадратными корнями, можете позволить себе время от времени прибегать к помощи онлайн-калькуляторов. Они помогут решать примеры быстрее и быть эффективнее.

Таких калькуляторов в интернете много, вот один из них.

Извлечение квадратного корня из большого числа

Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.

Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.

Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:

Извлечь корень из большого числа можно разными способами — вот один из них.

Извлечем корень из √2116.

Наша задача в том, чтобы определить между какими десятками стоит число 2116.

Мы видим что, 2116 больше 1600, но меньше 2500.

41, 42, 43, 44, 45, 46, 47, 48, 49.

Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.

Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.

Как пользоваться таблицей

4 2 = 16 ⇒ 6

5 2 = 25 ⇒ 5

6 2 = 36 ⇒ 6

7 2 = 49 ⇒ 9

8 2 = 64 ⇒ 4

9 2 = 81 ⇒ 1

Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.

Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.

Число 43, возведенное в квадрат, даст число, на конце которого — 9.

Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.

Далее вычисляем: 44 * 44 = 1936.

Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.

Еще пример. Извлечем корень из числа √11664

Разложим число 11664 на множители:

Запишем выражение в следующем виде:

Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.

Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.

Бесплатный курс от Екатерины Мурашовой

109004, Москва, ул. Александра Солженицына, 23а, строение 1, подъезд 10

Источник

Преобразование иррациональных выражений в математике с примерами решения и образцами выполнения

Иррациональными выражениями называют выражения, содержащие операцию извлечения корня. Другими словами, иррациональные выражения – это выражения с радикалами (выражения, содержащие в своей записи знаки корня).

Арифметический корень и его свойства

Определение арифметического корня: Пусть а—действительное число, a n — натуральное число, большее единицы. Поставим перед собой задачу: найти число х, такое, чтобы выполнялось равенство

Сначала рассмотрим конкретные примеры.

тогда равенство (1) принимает вид: откуда

тогда равенство (1) принимает вид: откуда

тогда равенство (1) принимает вид: что не выполняется ни при каком действительном значении х;

тогда равенство (1) принимает вид: откуда

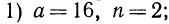
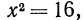
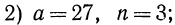
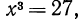
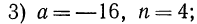
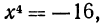
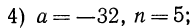
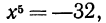
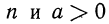
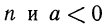
Эти примеры показывают, что поставленная задача при четном имеет два решения, при нечетном n —одно решение, при четном ни одного решения.

Если задача имеет решение, т. е. равенство 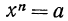выполняется при некоторых значениях х, то эти значения x называются корнями n-й степени из числа а итак корень n-й степени из числа а—это такое число, n-я степень которого равна а.

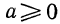
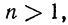
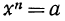
Рассмотрим случай отыскания корня n-й степени из неотрицательного числа. Можно доказать, что если и то существует и только одно неотрицательное число х, такое, что (доказательство проводится в курсе высшей математики; представление об этом доказательстве будет дано в следующей главе).

Арифметическим корнем n-й степени из положительного числа а называется такое положительное число, n-я степень которого равна а.

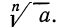
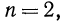
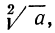
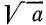
Для арифметического корня n-й степени из числа а принято обозначение Число а называется подкоренным числом или подкоренным выражением, n- показатель корня. Если то обычно не пишут а пишут просто и называют это выражение квадратным корнем. Часто вместо термина «корень» используется термин «радикал».

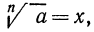
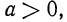
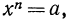
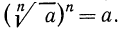
Согласно определению запись где означает, во-первых, что и, во-вторых, что т. е. Например,

Полагают также

Обратим внимание читателя на то, что, например,

Свойства арифметических корней

Условимся прежде всего о следующем: все переменные, которые встречаются в формулировках свойств и в примерах, рассматриваемых в настоящем и следующем пунктах, будем считать принимающими только неотрицательные значения. Кроме того, мы рассматриваем только арифметические корни, а потому каждый раз специально подчеркивать это не будем. Значит, мы будем писать: «корень n-й степени из неотрицательного числа», а читатель должен понимать, что речь идет об арифметическом корне.

1°. Корень n-й степени из произведения двух неотрицательных чисел равен произведению корней из этих чисел, т. е.

Доказательство:

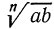
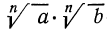
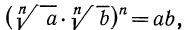
Мы знаем, что это такое неотрицательное число, которое, будучи возведено в степень n, дает подкоренное выражение ab. Ясно, что — неотрицательное число. Значит, если мы покажем, что то это и будет обозначать, что

Итак, рассмотрим выражение 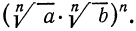По свойству 1° степени с натуральным показателем (стр. 45) имеем

Так как 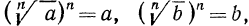то получаем

Пример. Вычислить

Решение. По свойству 1° имеем

2°. Корень n-й степени из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя, т. е.

Пример:

Доказательство этого свойства аналогично доказательству свойства 1°.

3°. Чтобы возвести корень n-й степени в натуральную степень k, достаточно возвести в эту степень подкоренное выражение и из полученного результата извлечь корень n-й степени, т. е.

Пример:

Доказательство:

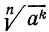
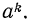
По определению корня это такое неотрицательное число, которое, будучи возведено в n-ю степень, дает Поэтому нам достаточно показать, что

По свойству 3° степени с натуральным показателем (стр. 45) имеем

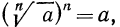
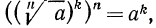
Так как то получаем т. е.

4°. Чтобы извлечь корень из корня, нужно перемножить показатели корней, а подкоренное выражение оставить без изменения, т. е.

Пример:

Доказательство:

значит,

5°. Если показатель корня и показатель степени подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится, т. е.

Пример:

Доказательство:

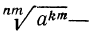
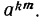
По определению корня это такое неотрицательное число, которое, будучи возведено в степень mn дает Значит, достаточно показать, что

По свойству 3° степени с натуральным показателем имеем

Значит,

Примеры:

Извлечь корень из произведения:

Решение:

а) Применив свойство 1° арифметических корней, получим:

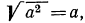
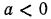
Напомним, что мы в начале рассматриваемого пункта условились считать все переменные принимающими только неотрицательные значения. Не будь этого соглашения, мы не имели бы права писать так как при это неверно; то же относится и к равенству

2. Извлечь корень из дроби

Решение:

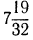
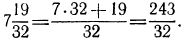
а) Обратим смешанное число в неправильную дробь: свойству 2° получаем

б) воспользовавшись свойствами 2° и 1°, получим

3.Вынести множитель из-под знака корня:

Решение:

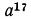
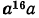
а) Представим подкоренное выражение в виде и применим к полученному произведению свойство 1° арифметических дробей:

Такое преобразование называется вынесением множителя из-под знака корня. Цель преобразования —упрощение подкоренного выражения;

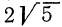
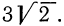
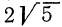
В некоторых случаях оказывается полезным преобразование, в определенном смысле обратное только что рассмотренному, а именно: внесение множителя под знак корня. Пусть, например, нужно выяснить, какое из чисел больше: или Рассмотрим число Внесем множитель 2 под знак корня —это достигается с помощью следующего преобразования:

Сделаем аналогичное преобразование числа

Так как

4.Ввести множитель под знак корня:

Решение:

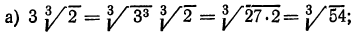
В рассмотренных примерах мы пользовались только определением корня и свойствами 1° и 2°. Рассмотрим теперь примеры использования свойств 3° и 4°.

Решение:

а) По свойству 3° имеем

Обычно стараются подкоренное выражение упростить, для чего выносят множители за знак корня. Имеем:

6.Выполнить действия:

Решение:

а) По свойству 4° арифметических корней имеем

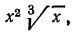
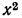
б) преобразуем выражение внеся множитель под знак корня:

Далее имеем

Рассмотрим, наконец, примеры, в которых используется свойство 5°.

Решение:

а) По свойству 5° мы имеем право показатель корня и показатель степени подкоренного выражения разделить на одно и то же натуральное число. Если в рассматриваемом примере разделить указанные показатели на 3, то получим

8.Упростить выражения:

Решение:

а) Из свойства 1° получаем, что для перемножения корней одной и той же степени достаточно перемножить подкоренные выражения, из полученного результата извлечь корень той же степени; значит,

в) выше мы видели, как перемножить корни одной и той же степени. В данном же примере требуется перемножить корни с различными показателями. Значит, прежде всего мы должны привести радикалы к одному показателю. Согласно свойству 5°, можно показатель корня и показатель степени подкоренного выражения умножить на одно и то же натуральное число; поэтому

А теперь разделим в полученном результате показатели корня и подкоренного выражения на 3:

г) приведем радикалы к одному показателю. Для этого, очевидно, нужно найти наименьшее общее кратное чисел 10 и 15; 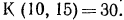Значит, нам нужно показатели корня и степени подкоренного выражения для первого из перемножаемых радикалов умножить на 3, а для второго—на 2; получим

д) НОК чисел 4, 6, 10 равно 60, поэтому приведем все радикалы к показателю 60:

Тождество

Ответим на такой вопрос: если переменная а принимает как неотрицательные, так и отрицательные значения, то чему равен

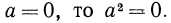
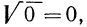
Если Но значит можно считать, что при справедливо равенство

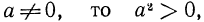
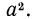
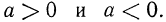
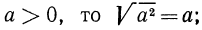
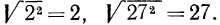
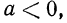
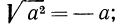
Если и речь, следовательно, идет об арифметическом корне второй степени из положительного числа Здесь могут представиться два случая: Если например, Если же то например,

Итак, можно записать, что

Но точно так же определяется модуль действительного числа

Таким образом, 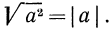Например,

Вообще, если n — четное число, т.е. 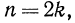то

Так, если в рассмотренных примерах 1, а) и б) снять требование неотрицательности значений переменных, то решение примера выглядело бы следующим образом:

Дополнительные замечания о свойствах радикалов

Рассмотренные пять свойств арифметических корней, т. е. пять свойств радикалов безоговорочно верны для неотрицательных подкоренных выражений. Но при решении примеров на действия с радикалами нужно иметь в виду возможность отрицательных значений переменных, содержащихся под знаками радикалов.

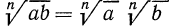
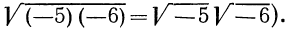
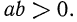
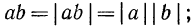
Пусть а и b — отрицательные числа, а n — четное число. В этом случае написать нельзя, так как 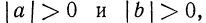правая часть такого «равенства» не имеет смысла (например, нельзя написать Здесь можно рассуждать так: а и b—отрицательные числа, следовательно, Но тогда значит,

Так как то, применив свойство 1° арифметических корней, получим

Итак, если n —четное число, а числа а и b имеют одинаковые знаки, то

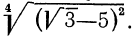
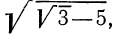
Очень внимательно следует относиться к свойству 5°. Пусть, например, нужно упростить выражение Если разделить показатели корня и подкоренного выражения на 2, то придем к выражению не имеющему смысла, так как под корнем четной степени содержится отрицательное число. Верное равенство в данном случае выглядит так:

В самом деле, 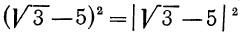и, следовательно,

Обобщение понятия о показателе степени

Постановка задачи: Напомним определение степени с натуральным показателем и ее свойства.

Определение

Основные свойства степени

В последующих пунктах речь пойдет об определениях степени с любым рациональным показателем.

Сначала мы определим степень с положительным дробным показателем, далее степень с нулевым показателем и затем степень с отрицательным рациональным показателем. Ясно, что ни на один из этих случаев не переносится данное выше определение, например 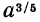нельзя определить как произведение числа а самого на себя 3/5 раза. Поэтому каждый раз придется вводить новое определение. При выборе нового определения мы будем руководствоваться требованием, чтобы на новый случай степени распространялись свойства, аналогичные свойствам 1°—5°, перечисленным выше.

Степень с положительным дробным показателем

Пусть Надо определить так, чтобы выполнялось, например, равенство т. е. чтобы при возведении степени в степень показатели перемножались. Но это равенство возможно лишь в случае, когда Возникает вполне естественная мысль: определить Но будет ли такое определение удачным, т. е. будут ли при таком определении выполняться свойства, аналогичные свойствам 1°—5°? Проверим это.

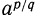
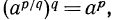
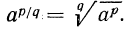
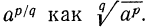
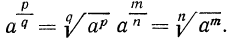
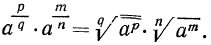
Доказательство. Согласно предложенному определению степени с положительным дробным показателем имеем: Значит, Воспользовавшись свойствами радикалов, приведем радикалы к одному показателю и выполним умножение:

Далее имеем 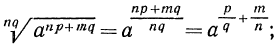значит,

Доказательство:

Воспользуемся свойствами возведения радикала в степень и извлечения корня из корня:

Аналогично можно показать, что будут выполняться свойства:

Итак, при предложенном определении степени с положительным дробным показателем основные свойства степени выполнены. Значит, определение удачно и его можно принять.

Определение:

Если

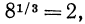
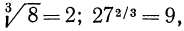
Например, так как так как

На практике при выполнении действий над радикалами довольно часто переходят к дробным показателям.

Примеры:

Выполнить умножение:

Решение:

2.Разложить на множители

Решение:

Степень с нулевым показателем

При выборе определения мы также будем руководствоваться требованием, чтобы на случай степени с нулевым показателем распространялись свойства 1°—5° степени с натуральным показателем (впрочем, теперь мы уже вправе говорить о распространении свойств степени с положительным рациональным показателем). В частности, при умножении степеней с одинаковым основанием показатели должны складываться, т. е. должно выполняться равенство

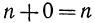
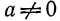
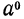
так как (n—натуральное число). Это равенство при возможно лишь в случае, когда Поэтому возникает мысль определить как 1. Нетрудно проверить, что при таком определении выполняются свойства, аналогичные свойствам 1° — 5° степени с натуральным показателем, значит, определение можно принять.

Определение:

Если

Например,

Степень с отрицательным рациональным показателем

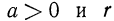
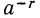
Пусть положительное рациональное число. Надо определить так, чтобы, например, выполнялось равенство

Покажем, например, что

Остальные свойства проверяются аналогично.

Определение:

Если

Например,

Замечание:

Если r—целое число, то полагают а 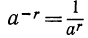и в случае, когда а Степень с любым рациональным показателем

Мы определили понятие степени с любым рациональным показателем. Эта степень обладает следующими свойствами (мы полагаем а > 0, b > 0, 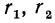— произвольные рациональные числа):

Заметим, что после введения нулевого и отрицательного показателей мы имеем право в свойстве 2° не делать оговорки, что

Тождественные преобразования иррациональных выражении

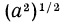
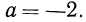
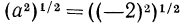
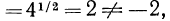
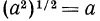
Тождественно равные выражения на данном множестве: По определению (стр. 47) тождественно равными выражениями называются такие, у которых все соответственные значения равны. Согласно этому определению выражения и а не являются тождественно равными. Действительно, пусть тогда т. е. равенство не является тождеством.

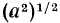
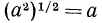
Однако на множестве всех неотрицательных чисел все соответственные значения выражений и а равны и равенство называют тождеством на этом множестве.

Определение:

Два выражения называются тождественно равными на данном множестве, если на этом множестве они имеют смысл и все их соответственные значения равны.

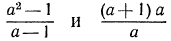
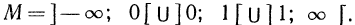
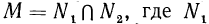
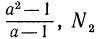
Например, выражения тождественно равны на множестве Легко видеть, что где TV, — множество, на котором определено выражение множество, на котором определено выражение

Тождественные преобразования иррациональных выражений

Выражение с переменными называется иррациональным, если оно содержит извлечение корня из переменной или возведение переменной в дробную степень.

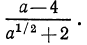
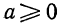
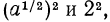
Тождественные преобразования иррациональных выражений выполняются, как правило, на множестве неотрицательных чисел. Это вытекает из введенных ранее определений. Например, сократим дробь При выражение а — 4 можно представить в виде разности квадратов выражений а затем сократить дробь:

Проделанное нами тождественное преобразование выполнено на множестве неотрицательных чисел, т. е. при В дальнейшем мы будем это подразумевать и специально не оговаривать.

Примеры:

Решение:

Здесь целесообразно применить прием избавления от иррациональности в знаменателе. Для этого умножим числитель и знаменатель первой дроби на 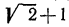(это выражение называется сопряженным для

Аналогично поступим со второй дробью (теперь выражением, сопряженным для знаменателя, является

Для того чтобы избавиться от иррациональности в знаменателе третьей дроби, умножим числитель и знаменатель этой дроби на

Таким образом, имеем

Решение:

Прежде всего подумаем, нельзя ли сократить первую дробь. Выражение, стоящее в числителе, можно преобразовать так:

Таким образом, последовательное сокращение дробей при тождественных преобразованиях иррациональных выражений обеспечивает достаточную простоту решения. Проиллюстрируем эту мысль еще на одном примере.

Решение:

Попытка привести дроби, стоящие в числителе, к общему знаменателю без предварительных сокращений этих дробей приведет решение к неоправданному усложнению. Поэтому в первую очередь надо сократить эти дроби, а затем произвести указанные действия:

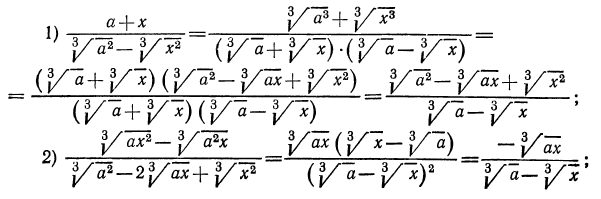
Идея сокращения дробей лежит и в основе тождественных преобразований выражений, содержащих степени с рациональными показателями.

Решение:

Подчеркнем, что проделанные нами в примере 4 тождественные преобразования выполнены на множестве положительных чисел, т. е. при

Иногда множество, на котором выполняются преобразования, имеет более сложную природу. Поясним это на следующем примере.

Решение:

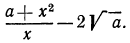
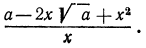
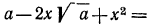
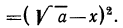
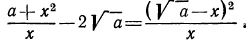
Рассмотрим выражение Оно преобразуется к виду Замечаем, что Итак, Аналогично

После этих наблюдений мы можем заданное выражение переписать в виде

Выше мы отмечали, что 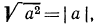поэтому

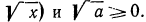
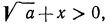
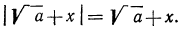
По смыслу примера имеем (заданное выражение содержит Значит, а потому Таким образом, мы приходим к выражению

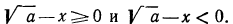
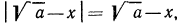
Теперь нужно рассмотреть два случая: В первом случае а во втором

Ответ:

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник