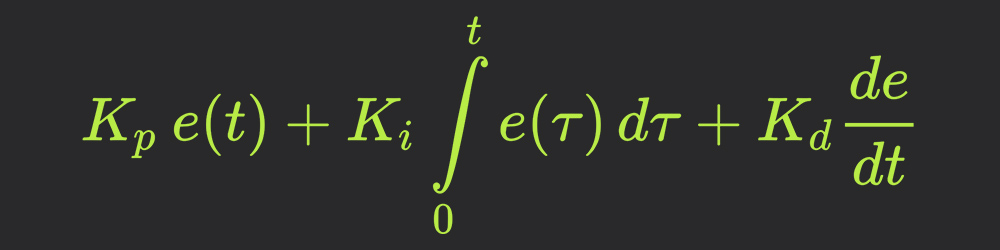подбор параметров пид регулятора
Простой метод настройки ПИД регулятора

Есть два похода к настройке ПИД регулятора. Первый – синтез регулятора, то есть вычисление параметров регулятора на основании модели системы. Данный метод позволяет очень точно рассчитать параметры регулятора, но он требует основательного погружения в ТАУ.
Второй метод – ручной подбор параметров (коэффициентов). Это метод научного тыка проб и ошибок. Берем готовую систему, меняем один (или сразу несколько коэффициентов) регулятора, включаем регулятор и смотрим за работой системы. В зависимости от того, как ведет себя система с выбранными коэффициентами (недо/пере регулирование) опять меняем коэффициенты и повторяем эксперимент. И т. д. Ну, такой метод имеет право на жизнь, главное представлять как изменение того или иного коэффициента повлияет на систему (что бы не действовать совсем наугад).
Есть более «оптимизированный» метод подбора коэффициентов – метод Зиглера–Никольса.
Сразу скажу, что метод работает не для любой системы, результаты получаются не самыми оптимальными. Но, зато, метод очень простой и годится для базовой настройки регулятора в большинстве систем.
Суть метода состоит в следующем:
1. Выставляем все коэффициенты (Kp, Ki, Kd) в 0.
2. Начинаем постепенно увеличивать значение Kp и следим за реакцией системы. Нам нужно добиться, чтобы в системе начались устойчивые колебания (вызванные перерегулированием). Увеличиваем Kp, пока колебания системы не стабилизируются (перестанут затухать).
3. Запоминаем текущее значение Kp (обозначим его Ku) и замеряем период колебаний системы (Tu).
Все. Теперь используем полученные значения Ku и Tu для расчета всех параметров ПИД регулятора по формулам:
Kp = 0.6 * Ku
Ki = 2 * Kp / Tu
Kd = Kp * Tu / 8
Готово. Для дискретных регуляторов нужно еще учесть период дискретизации – T ( умножить на Ki та Т, разделить Kd на Т).
Еще раз повторюсь, ТАУ изучать нужно, синтез регуляторов рулит, описанный метод годится для базовой настройки, подходит не для всех систем и т. д. Но данный метод очень простой, и вполне годится для «бытового» уровня.
Настройка ПИД-регулятора
Для простоты изложения рассмотрим настройку регулятора на примере. Допустим, необходимо поддерживать температуру в помещении с помощью обогревателя, управляемого регулятором. Для измерения текущей температуры используем термопару.
Задача настройки
Настройка регулятора производится с одной единственной целью: подобрать его коэффициенты для данной задачи таким образом, чтобы регулятор поддерживал величину физического параметра на заданном уровне. В нашем примере физическая величина — это температура.
Допустим текущая температура в помещении 10 °С, а мы хотим, чтобы было 25°С. Мы включаем регулятор и он начинает управлять мощностью обогревателя таким образом, чтобы температура достигла требуемого уровня. Посмотрим как это может выглядеть.

Чёрным цветом показан график изменения температуры в том случае, если коэффициенты подобраны совсем плохо. Система теряет устойчивость. Регулятор при этом идёт «в разнос» и температура «уходит» от заданного значения.
Рассмотрим более благоприятные случаи.

А вот и приемлемые кривые:

В процессе настройки регулятора, пользователю необходимо стремиться получить кривую, близкую к идеальной. Однако, в реальных условиях сделать это не так-то просто — приходится долго и мучительно подбирать коэффициенты. Поэтому зачастую останавливаются на «приемлемой» кривой регулирования. Например, в нашем примере нас могли бы устроить коэффициенты регулятора, при которых заданная температура достигалась бы за 15-20 минут с максимальным перерегулированием (максимальными «скачками» температуры) 2 °С. А вот время достижение уставки более часа и максимальные «скачки» температуры 5 °С — нас бы не устроили.
Далее поговорим о том, как подобрать коэффициенты для достижения оптимального регулирования. Рекомендуется настраивать коэффициенты в том же порядке, в котором это описано.
Настраиваем пропорциональный коэффициент
Выставляем дифференциальный и интегральный коэффициенты в ноль, тем самым убирая соответствующие составляющие. Пропорциональный коэффициент выставляем в 1.
Далее нужно задать значение уставки температуры отличное от текущей и посмотреть, как регулятор будет менять мощность обогревателя, чтобы достичь заданного значения. Характер изменения можно отследить «визуально», если у вас получится мысленно представить этот график. Либо можно регистрировать в таблицу измеренное значение температуры каждые 5-10 секунд и по полученным значением построить график. Затем нужно проанализировать полученную зависимость в соответствии с рисунком:

Настраиваем дифференциальный коэффициент
Постепенно увеличивая дифференциальную составляющую, необходимо добиться уменьшения или полного исчезновения «скачков» графика (перерегулирования) перед выходом на уставку. При этом кривая должна стать еще больше похожа на идеальную. Если слишком сильно завысить дифференциальный коэффициент, температура при выходе на уставку будет расти не плавно, а скачками (как показано на рисунке).
При появлении таких скачков необходимо прекратить увеличение дифференциального коэффициента.
Настраиваем интегральный коэффициент
При настройке двух предыдущих коэффициентов можно получить практически идеальную кривую регулирования или близкую к ней кривую, удовлетворяющую условиям задачи. Однако, как правило возникает так называемая «статическая ошибка». При этом в нашем примере температура стабилизируется не на заданном значении 25 °С, а на несколько меньшем значении. Дело в том, что если температура станет равной уставке (то есть разность текущей и заданной температур станет равна 0), то пропорциональная и дифференциальная составляющая будут равны нулю ( см. функцию преобразования ПИД-регулятора ). При этом мощность регулятора тоже станет равна 0 и он начнёт остывать.
Для того чтобы исключить этот эффект, используют интегральную составляющую. Её необходимо постепенно увеличивать до исчезновение статической ошибки. Однако, чрезмерное её увеличение тоже может привести к возникновению скачков температуры.
Заключение
Настройка ПИД-регулятора довольно сложный и трудоёмкий процесс. На практике достаточно тяжело достичь оптимального регулирования и зачастую в этом нет необходимости. Чаще всего достаточно добиться такого вида переходного процесса, который устроит пользователя в условиях текущей задачи.
ПИД-регулятор. Методика настройки
2020-07-10 

ПИД-регулятор (пропорционально-интегрально-дифференциальный) — устройство, с обратной связью, применяемое в автоматических системах управления для поддержания заданного значения параметра. Благодаря своей универсальности они широко применяются в различных технологических процессах.
Выходной сигнал регулятора определяется по следующей формуле:
u (t) = P + I + D = Kp e (t) + Ki ∫e (t) dt + Kd de (t)/dt
u (t) – выходной сигнал регулятора;
P – пропорциональная составляющая;
I – интегрирующая составляющая;
D – дифференцирующая составляющая;
Ki — интегральный коэффициент
Kd – дифференциальный коэффициент
e (t) – ошибка рассогласования
Задачи ПИД-регулятора в системах АСУ ТП
Основная задача ПИД регулятора состоит в поддержании определенного значения параметра технологического процесса на заданном уровне. То есть говоря простым языком, задача ПИД-регулятора заключается в том, чтобы учитывая полученные значения с датчиков (обратная связь) воздействовать на объект управления, плавно подводя регулируемое значение к заданным уставкам. Применение ПИД регуляторов целесообразно, а зачастую и единственно возможно в процессах, где необходима высокая точность переходных процессов, непрерывный контроль и регулирование заданных параметров, недопустимы значительные колебания в системе.
Сравнение ПИД –регулятора с позиционным регулированием
В системах АСУ ТП наибольшее распространение получили два типа регуляторов – двухпозиционный и ПИД.
Двухпозиционный регулятор наиболее простой в использовании и широко распространенный.
Данный тип регулятора сравнивает значение входной величины с заданным параметром уставки. Если значение измеренной величины ниже заданного значения уставки, регулятор включает исполнительное устройство, при превышении заданного значения, исполнительное устройство выключается. Для предотвращения слишком частого срабатывания устройства, в следствии колебаний системы и следовательно изменении значений, задается минимальный и максимальный порог срабатывания — гистерезис, или по другому зона нечувствительности, мертвая зона, дифференциал. Например, нам необходимо поддерживать температуру в 15°С. Если гистерезис задан 2°, то регулятор будет включать нагрев при 14°С и отключать соответственно при 16°С.
Так или иначе, при таком типе регулирования происходят незатухающие колебания, частота и амплитуда которых зависит от параметров системы. Поэтому данный метод обеспечивает хороший результат в системах, обладающих инерционностью и малым запаздыванием. В частности, такой метод широко применяется при регулировании температуры в нагревательных печах.
В отличии от двухпозиционного с помощью ПИД-регулятора удается свести колебания системы к минимуму, благодаря тому, что при таком методе регулирования учитываются различные значения системы — фактическая величина, заданное значение, разность, скорость. Это позволяет стабилизировать систему и добиться повышения точности в десятки раз по сравнению с двухпозиционным методом. Конечно, здесь многое зависит от правильно подобранных коэффициентов ПИД регулятора.
Составляющие ПИД-регулятора
В стандартном ПИД-регуляторе есть три составляющие и каждая из них по своему воздействует на управление.
Пропорциональная — P (t) = Kp * e (t)
Учитывает величину рассогласования заданного значения и фактического. Чем больше отклонения значения, тем больше будет выходной сигнал, то есть пропорциональная составляющая пытается компенсировать эту разницу.
Однако пропорциональный регулятор не способен компенсировать полностью ошибку рассогласования. Всегда будет присутствовать так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. При увеличении коэффициента пропорциональности Kp статическая ошибка уменьшается, но могут возникнуть автоколебания и снижение устойчивости системы.
Интегральная – I (t) = Ki ∫e (t) dt
Интегральная составляющая используется для устранения статической ошибки. Она складывает значение предыдущих ошибок рассогласования и компенсирует их, можно сказать, что учится на предыдущих ошибках. То есть ошибка рассогласования умножается на коэффициент интегрирования и прибавляется к предыдущему значению интегрирующего звена. При выходе системы на заданный режим, интегральная составляющая перестает изменяться и не оказывает какого-либо серьезного воздействия на систему. Физически интегральная составляющая представляет задержку реакции регулятора на изменение величины рассогласования, внося в систему некоторую инерционность, что может быть полезно для управления объектами c большой чувствительностью.
Дифференциальная – D (t) = Kd de (t)/dt
Дифференциальная составляющая учитывает скорость изменения регулируемой величины, противодействуя предполагаемым отклонениям, вызванными возмущениями системы или запаздыванием. И чем больше будет величина отклоняться от заданной, тем сильнее будет противодействие, оказываемое дифференциальной составляющей. То есть она предугадывает поведение системы в будущем. При достижении величины рассогласования постоянного значения дифференциальная составляющая перестает оказывать воздействие на управляющий сигнал.
На практике какая-либо из составляющих может не использоваться (чаще всего Д-дифференциальная) и тогда мы получаем П-регулятор, ПИ-регулятор.
Методика настройки ПИД-регулятора
Выбор алгоритма управления и его настройка является основной задачей в процессе проектирования и последующего удовлетворительного запуска агрегата в промышленную или иную эксплуатацию.
В основе методики лежит закон Циглера-Никольса, являющийся эмпирическим и основанным на использовании данных, полученных экспериментально на реальном объекте.
В результате ознакомления с методикой, а также при близком рассмотрении объектов регулирования, были выбраны формулы и коэффициенты ближе всего подходящие к реальному объекту регулирования.
Объект регулирования – камерная электрическая печь. Число зон регулирования от 24 до 40. Каждая зона есть набор электронагревателей. Материал нагревателей нихром. Тип — проволочные, навитые на керамические трубки.
Требования: поддержание температуры по зонам печи +/- 5С.
МЕТОДИКА:
Настройка пропорциональной компоненты (Xp)
Тο — начальная температура в системе;
Тsp — заданная температура (уставка);
∆T — размах колебаний температуры;
∆t — период колебаний температуры.
Система должна находится в постоянном колебательном процессе, притом колебательный процесс незатухающий, где ∆T– характеристика колебания равная значению величины рассогласования (±10С, или как по заданию). Колебания должны быть одинаковы от Тsp.
После получения данной кривой на нашем объекте, засекаем время периода колебаний ʌt – полный период. Данное время есть характеристика системы, оборудования.
3. Используя полученные параметры рассчитываем Ти и Тд.
| Зона пропорциональности | Коэффициент передачи | Постоянная времени интегрирования | Постоянная времени дифференцирования | |
| П-регулятор | 2*PBs | 0.5*Xp | ||
| ПИ-регулятор | 2.2*PBs | 0.45*Xp | 0.83*ʌТ | |
| ПИД-регулятор | 1.67*PBs | 0.6*Xp | 0.5*ʌТ | 0.125*ʌТ |
Цифры в формулах для расчета коэффициентов ПИД-регулирования скорректированы на основе запуска камерной электрической печи в опытно-промышленную эксплуатацию. И конечно в зависимости от типа объекта регулирования могут незначительно меняться.
Вывод
Благодаря достаточно высоким получаемым результатам ПИД-регуляторы нашли широкое применение в системах автоматического управления.
При этом важно подчеркнуть, что настройка ПИД-регулятора является процессом довольно трудоемким и требует определенных знаний и индивидуального подхода для различных объектов управления.
Настройка ПИД-регуляторов: так ли страшен чёрт, как его малюют? Часть 1. Одноконтурная система
Эта статья открывает цикл статей, посвященных автоматизированным способам настройки ПИД-регуляторов в среде Simulink. Сегодня разберемся, как работать с приложением PID Tuner.
Введение
Наиболее популярным типом применяемых в промышленности регуляторов в системах управления замкнутыми системами можно считать ПИД-регуляторы. И если структуру и принцип действия контроллера инженеры помнят еще со студенческой скамьи, то его настройка, т.е. расчет коэффициентов регулятора, до сих пор является проблемой. Существует огромное количество литературы, как зарубежной (например, [1, 2]), так и отечественной (например, [3, 4]), где настройка регуляторов объясняется на достаточно непростом языке теории автоматического управления.
В этой серии статей будут описываться автоматизированные способы настройки ПИД-регуляторов с помощью инструментов среды Simulink, таких как:
В качестве объекта системы управления будет выступать электропривод на базе двигателя постоянного тока с возбуждением от постоянных магнитов, работающий совместно с редуктором на инерционную нагрузку, со следующими параметрами:
Параметры нагрузки и редуктора:
Статьи практически не содержат математических формул, однако желательно, чтобы читатель обладал базовыми знаниями в теории автоматического управления, а также имел опыт моделирования в среде Simulink для понимания предлагаемого материала.
Модель системы
Рассмотрим линейную систему управления угловой скоростью следящего электропривода, упрощенная структурная схема которой представлена ниже.
В соответствии с приведенной структурой в среде Simulink была построена модель такой системы.
Модели электропривода (подсистема Electric actuator) и инерционной нагрузки (подсистема Load) созданы с помощью блоков библиотеки физического моделирования Simscape:
Модели электропривода и нагрузки также включают подсистемы датчиков различных физических величин:
Перед настройкой параметров ПИД-регулятора запустим модель на расчет, приняв передаточную функцию регулятора . Результаты моделирования при отработке входного сигнала 150 об/мин показаны ниже.
Из анализа приведенных графиков видно, что:
Пусть реакция системы на единичный импульс должна соответствовать следующим требованиям:
Кроме того, регулятор должен ограничивать напряжение, подаваемое на обмотку двигателя, до значения напряжения питания.
Настраиваем контроллер
Настройка параметров регулятора осуществляется с помощью инструмента PID Tuner, который доступен непосредственно в окне параметров блока PID Controller.
Приложение запускается нажатием на кнопку Tune…, расположенную на панели Automated tuning. Стоит отметить, что до выполнения этапа настройки параметров контроллера необходимо выбрать его вид (П, ПИ, ПД и др.), а также его тип (аналоговый или дискретный).
Поскольку одним из требований является ограничение его выходной координаты (напряжения на обмотке двигателя), то следует задать допустимый диапазон напряжений. Для этого:
Корректная работа блока регулятора в составе системы предполагает использования методов, направленных на борьбу с интегральным насыщением. В блоке реализованы два метода: back-calculation и clamping. Подробная информация о данных методах располагается здесь. Выпадающее меню выбора метода расположено на панели Anti-windup.
Можно заметить, что внешний вид блока регулятора изменился: появился знак насыщения рядом с выходным портом блока.
Далее, приняв все изменения нажатием кнопки Apply, возвращаемся во вкладку Main и нажимаем кнопку Tune…, в результате чего откроется новое окно приложения PIDTuner.
В графической области окна отображаются два переходных процесса: при текущих параметрах регулятора, т.е. для ненастроенного регулятора, и при значениях, подобранных автоматически. Новые значения параметров можно посмотреть, нажав на кнопку Show Parameters, расположенную на панели инструментов. При нажатии на кнопку появятся две таблицы: подобранные параметры регулятора (Controller Parameters) и произведенные оценки характеристик переходного процесса при подобранных параметрах (Performance and Robustness).
Как видно из значений второй таблицы, автоматически рассчитанные коэффициенты регулятора удовлетворяют всем требованиям.
Настройка регулятора завершается нажатием на кнопку с зеленым треугольником, расположенной справа от кнопки Show Parameters, после чего новые значения параметров автоматически изменятся в соответствующих полях в окне настройки параметров блока PID Controller.
Результаты моделирования системы с настроенным регулятором для нескольких входных сигналов показаны ниже. При больших уровнях входных сигналов (голубая линия) система будет работать в режиме с насыщением по напряжению.
Отметим, что инструмент PID Tuner подбирает коэффициенты регулятора по линеаризованной модели, поэтому при переходе к нелинейной модели требуется уточнять его параметры. В этом случае можно воспользоваться приложением Response Optimizer.
ПИД регулятор
ПИД регулятор – один из самых распространенных автоматических регуляторов. Он настолько универсален, что применяется практически везде, где нужно автоматическое управление. Например температурой: специальные печи, холодильники, инкубаторы, паяльники, сопло и стол 3D принтера, ИК паяльные станции и прочее. Поддержание частоты оборотов мотора, например для станков. Всевозможные балансирующие штуки, гироскутеры, сигвеи, левитирующие магнитные платформы, и конечно же квадрокоптеры и самолёты с автопилотом. Это всё ПИД регулятор. Почему именно ПИД? Существуют и другие регуляторы, превосходящие ПИД по адаптивности к управляемой системе и стабильности, например линейно квадратичный. Но, чтобы грамотно синтезировать такой регулятор, нужно быть гораздо больше чем “семи пядей” во лбу, а настройка ПИД регулятора дело хоть и неприятное, но фактически очень простое и под силу любому, а сам ПИД регулятор универсален для почти любого процесса.
Система управления
Прежде чем переходить непосредственно к пиду, очень важно понять и запомнить несколько базовых понятий, из которых состоит автоматическая система. В первую очередь это регулятор, который всем заправляет и находится в центре системы. Регулятор в данном понимании – математический алгоритм или часть программы, которая крутится на микроконтроллере. Регулятор, как алгоритм, работает с обычными числами. Объект управления – это девайс, которым мы управляем, например печка или мотор. Для этого у нас есть управляющее устройство, например диммируемый тен или драйвер мотора. Управляющее устройство получает от регулятора управляющий сигнал, то есть конкретное число. Это может быть заполнение шим сигнала, от 0 до 255, а может быть угол поворота сервомашинки от 0 до 180, потому что регулятору без разницы чем управлять. В объекте управления у нас стоит датчик, с которого регулятор получает управляемую величину, то есть текущий сигнал с датчика. Это – обратная связь, которая и даёт возможность системе ирчно поддержать заданное значение. В случае с печкой это температура, а с мотором – частота оборотов. Ну и наконец регулятор получает установку (уставку), то есть число, к которому он должен привести текущее значение с датчика. Установка может задаваться каким угодно образом: крутилкой, ползунком, энкодером, кнопками, да хоть смской или голосовым вводом. Регулятору это неважно, для него это просто цифра. Задача регулятора состоит в том, чтобы сравнивать текущее значение с установкой и выдавать управляющий сигнал на управляющее устройство. То есть в программе это будет выглядеть условно так: регулятор получил установку, регулятор получил значение с датчика, регулятор выполнил вычисления и выдал нам управляющий сигнал, опять же число. Если это шим – мы его подаём через функцию генерации шим. Есть ещё один момент – регулятор должен делать расчёты и применять управляющий сигнал через равные промежутки времени, то есть с равным периодом или частотой. Эта частота называется частотой дискретизации системы, а период обозначается как dt, прямо как период интегрирования.
Под капотом у ПИД регулятора
ПИД регулятор состоит из трёх составляющих: пропорциональной P, интегрирующей I и дифференциирующей D, формируется просто как сумма трёх значений, умноженных каждая на свой коэффициент. Эта сумма после вычислений становится управляющим сигналом, который подаётся на управляющее устройство, обозначим его как out.
kP, kI и kD это и есть те самые коэффициенты, которые нужно настроить для работы ПИДа. Значения тут могут быть самые разные, от 0.001 то десятков и тысяч, это зависит от конкретной системы. Тут есть ещё один момент: любой коэффициент может быть равен нулю, и в таком случае обнуляется вся его компонента. То есть регулятор можно превратить в П, ПИ, ПД, и прочие сочетания. Разные системы требуют разного подхода, именно поэтому ПИД регулятор такой универсальный. В дальнейшем будем пользоваться следующими названиями переменных:
P составляющая
Пропорциональная составляющая предоставляет собой разность текущего значения с датчика и установки.
Данная разность называется ошибкой регулирования, то есть насколько далеко находится система от заданного значения. Получается чем больше ошибка, тем больше будет управляющий сигнал и тем быстрее система будет приводить управляемую величину к заданному значению. Коэффициент kP тут влияет роль усиления ошибки и настраивается вручную. Но в то же время, если система пришла к заданной величине, ошибка станет равной нулю, и управляющий сигнал тоже! Другими словами, п регулятор никогда не сможет привести к заданному значению, всегда будет некая ошибка. П составляющая является основной в ПИД регуляторе и так сказать тянет самую большую лямку, регулятор может неплохо работать только лишь на ней одной. P составляющая исправляет ошибку в текущий момент времени.
I составляющая
Интегральная составляющая просто суммирует в саму себя ту же самую ошибку, разность текущего и заданного значения, умноженную на период дискретизации системы, то есть на время, прошедшее с предыдущего расчёта dt – фактически берёт интеграл от ошибки по времени.
В самом регуляторе это ещё умножается на коэффициент kI, которым настраивается резкость данной составляющей. В интегральной составляющей буквально копится ошибка, что позволяет регулятору с течением времени полностью её устранить, то есть привести систему ровно к заданному значению с максимальной точностью. I составляющая исправляет прошлые, накопившиеся ошибки.
D составляющая
Дифференциальная составляющая представляет собой разность текущей и предыдущей ошибки, поделенную на время между измерениями, то есть на ту же dt, которая общий период регулятора. Иными словами – это производная от ошибки по времени.
Фактически D составляющая реагирует на изменение сигнала с датчика, и чем сильнее происходит это изменение, тем большее значение прибавляется к общей сумме. Иными словами, D позволяет компенсировать резкие изменения в системе и при правильной настройке предотвратить сильное перерегулирование и уменьшить раскачку. Коэффициент д позволяет настроить вес, или резкость данной компенсации, как и остальные коэффициенты регулируют свои составляющие. D составляющая в первую очередь нужна для быстрых систем, то есть для систем с резкими изменениями, такие как квадрокоптер или шпиндель станка под переменной нагрузкой. D составляющая исправляет возможные будущие ошибки, анализируя скорость.
Настройка регулятора
Для настройки регулятора нужно варьировать коэффициенты:
Вот так выглядит процесс стабилизации при изменении коэффициентов: 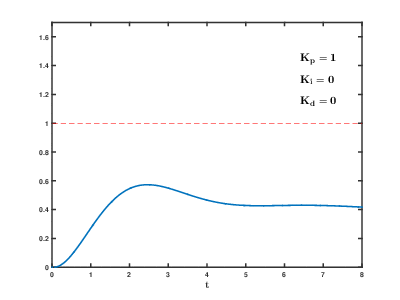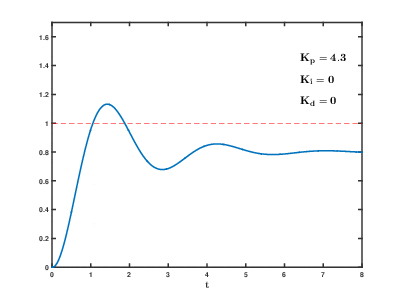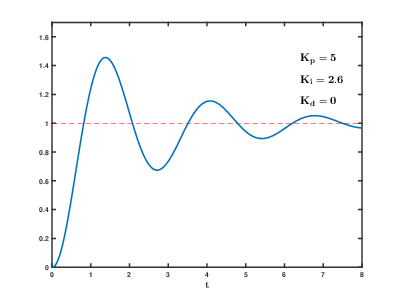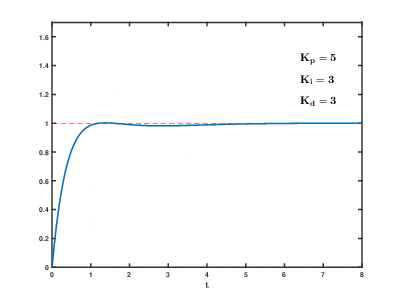
Например, незатухающие колебания появились при kP 20, период колебаний составил 3 секунды. Период dt в системе будет 50 мс (0.05 с). Считаем:
На полученных коэффициентах должны более-менее работать большинство систем, но не все. Также можно воспользоваться автоматическим тюнером коэффициентов, например два разных алгоритма встроены в библиотеку GyverPID.
Реализация на C++
Соединяя все рассмотренные выше уравнения, получим:
Это готовая функция, которая принимает значение с датчика, установку, три коэффициента и время, а также ограничение выхода с регулятора. Как пользоваться этой функцией: функция должна вызываться с некоторым периодом, причем длительность этого периода нужно будет передать в функцию в секундах. Если попроще, можно использовать задержку. Но делать так не рекомендуется, лучше сделать таймер на миллис и работать с ним. Функция возвращает управляющий сигнал, то есть можно подать его например как ШИМ. Период dt имеет такой смысл: чем инерционнее у нас система, тем реже можно вычислять пид. Например для обогрева комнаты период можно поставить 1 секунду или больше, а для контроля за оборотами двигателя надо будет поставить пару десятков миллисекунд, то есть около сотни раз в секунду.