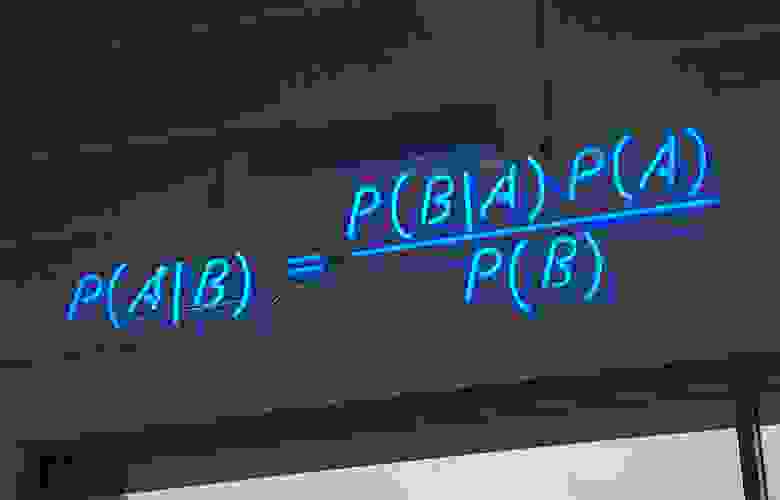понятие доверительного интервала неизвестного параметра распределения

Доверительные интервалы

Определение

Доверительные интервалы (англ. Confidence Intervals) одним из типов интервальных оценок используемых в статистике, которые рассчитываются для заданного уровня значимости. Они позволяют сделать утверждение, что истинное значение неизвестного статистического параметра генеральной совокупности находится в полученном диапазоне значений с вероятностью, которая задана выбранным уровнем статистической значимости.

Нормальное распределение

Когда известна вариация (σ 2 ) генеральной совокупности данных, для расчета доверительных пределов (граничных точек доверительного интервала) может быть использована z-оценка. По сравнению с применением t-распределения, использование z-оценки позволит построить не только более узкий доверительный интервал, но и получить более надежные оценки математического ожидания и среднеквадратического (стандартного) отклонения (σ), поскольку Z-оценка основывается на нормальном распределении.

Формула

Для определения граничных точек доверительного интервала, при условии что известно среднеквадратическое отклонение генеральной совокупности данных, используется следующая формула

где X – математическое ожидание выборки, α – уровень статистической значимости, Z_α/2 – Z-оценка для уровня статистической значимости α/2, σ – среднеквадратическое отклонение генеральной совокупности, n – количество наблюдений в выборке. При этом, σ/√ n является стандартной ошибкой.

Таким образом, доверительный интервал для уровня статистической значимости α можно записать в виде

Пример

Предположим, что размер выборки насчитывает 25 наблюдений, математическое ожидание выборки равняется 15, а среднеквадратическое отклонение генеральной совокупности составляет 8. Для уровня значимости α=5% Z-оценка равна Z_α/2=1,96. В этом случае нижняя и верхняя граница доверительного интервала составят

А сам доверительный интервал может быть записан в виде

Таким образом, мы можем утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности попадет в диапазон от 11,864 до 18,136.

Методы сужения доверительного интервала

Допустим, что диапазон [11,864; 18,136] является слишком широким для целей нашего исследования. Уменьшить диапазон доверительного интервала можно двумя способами.

Снизив уровень статистической значимости до α=10%, мы получим Z-оценку равную Z_α/2=1,64. В этом случае нижняя и верхняя граница интервала составят

А сам доверительный интервал может быть записан в виде

В этом случае, мы можем сделать предположение, что с вероятностью 90% математическое ожидание генеральной совокупности попадет в диапазон [12,376; 17,624].

Если мы хотим не снижать уровень статистической значимости α, то единственной альтернативой остается увеличение объема выборки. Увеличив ее до 144 наблюдений, получим следующие значения доверительных пределов

Сам доверительный интервал станет иметь следующий вид

Таким образом, сужение доверительного интервала без снижения уровня статистической значимости возможно только лишь за счет увеличения объема выборки. Если увеличение объема выборки не представляется возможным, то сужение доверительного интервала может достигаться исключительно за счет снижения уровня статистической значимости.

Построение доверительного интервала при распределении отличном от нормального

В случае если среднеквадратичное отклонение генеральной совокупности не известно или распределение отлично от нормального, для построения доверительного интервала используется t-распределение. Это методика является более консервативной, что выражается в более широких доверительных интервалах, по сравнению с методикой, базирующейся на Z-оценке.

Формула

Для расчета нижнего и верхнего предела доверительного интервала на основании t-распределения применяются следующие формулы

где X – математическое ожидание выборки, α – уровень статистической значимости, t_α – t-критерий Стьюдента для уровня статистической значимости α и количества степеней свободы (n-1), σ – среднеквадратическое отклонение выборки, n – количество наблюдений в выборке.

Сам доверительный интервал может быть записан в следующем виде

Распределение Стьюдента или t-распределение зависит только от одного параметра – количества степеней свободы, которое равно количеству индивидуальных значений признака (количество наблюдений в выборке). Значение t-критерия Стьюдента для заданного количества степеней свободы (n) и уровня статистической значимости α можно узнать из справочных таблиц.

Пример

Предположим, что размер выборки составляет 25 индивидуальных значений, математическое ожидание выборки равно 50, а среднеквадратическое отклонение выборки равно 28. Необходимо построить доверительный интервал для уровня статистической значимости α=5%.

В нашем случае количество степеней свободы равно 24 (25-1), следовательно соответствующее табличное значение t-критерия Стьюдента для уровня статистической значимости α=5% составляет 2,064. Следовательно, нижняя и верхняя граница доверительного интервала составят

А сам интервал может быть записан в виде

Таким образом, мы можем утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности окажется в диапазоне [38,442; 61,558].

Использование t-распределения позволяет сузить доверительный интервал либо за счет снижения статистической значимости, либо за счет увеличения размера выборки.

Снизив статистическую значимость с 95% до 90% в условиях нашего примера мы получим соответствующее табличное значение t-критерия Стьюдента 1,711.

В этом случае мы можем утверждать, что с вероятностью 90% математическое ожидание генеральной совокупности окажется в диапазоне [40,418; 59,582].

Если мы не хотим снижать статистическую значимость, то единственной альтернативой будет увеличение объема выборки. Допустим, что он составляет 64 индивидуальных наблюдения, а не 25 как в первоначальном условии примера. Табличное значение t-критерия Стьюдента для 63 степеней свободы (64-1) и уровня статистической значимости α=5% составляет 1,998.

Это дает нам возможность утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности окажется в диапазоне [43,007; 56,993].

Выборки большого объема

К выборкам большого объема относятся выборки из генеральной совокупности данных, количество индивидуальных наблюдений в которых превышает 100. Статистические исследования показали, что выборки большего объема имеют тенденцию быть нормально распределенными, даже если распределение генеральной совокупности отличается от нормального. Кроме того, для таких выборок применение z-оценки и t-распределения дают примерно одинаковые результаты при построении доверительных интервалов. Таким образом, для выборок большого объема допускается применение z-оценки для нормального распределения вместо t-распределения.

Подведем итоги

В таблице собраны рекомендации по выбору методики построения доверительных интервалов для различных ситуаций.

Источник

О формуле Байеса, прогнозах и доверительных интервалах

На Хабре много статей по этой теме, но они не рассматривают практических задач. Я попытаюсь исправить это досадное недоразумение. Формула Байеса применяется для фильтрации спама, в рекомендательных сервисах и в рейтингах. Без нее значительное число алгоритмов нечеткого поиска было бы невозможно. Кроме того, это формула явилась причиной холивара среди математиков.

Введение

Начнем издалека. Если наступление одного события увеличивает или уменьшает вероятность наступления другого, то такие события называются зависимыми. Тервер не изучает причинно-следственные связи. Поэтому зависимые события не обязательно следствия друг-друга, связь может быть не очевидной. Например, «у человека голубые глаза» и «человек знает арабский» — зависимые события, поскольку у арабов голубые глаза встречаются крайне редко.

Давайте подумаем чему равно вероятность наступления двух событий одновременно. P(AB). Вероятности наступления первого события умноженной на вероятность наступления второго события, в случае наступления первого. P(AB)=P(A)P(B|A). Теперь, если вспомнить, что P(AB)= P(BA). Получим, P(A)P(B|A)=P(B)P(A|B). Перенесем P(B) влево и получим формулу Байеса:

Все настолько просто, что 300 лет тому назад эту формулу вывел простой священник. Но это не уменьшает практической ценности этой теоремы. Она позволяет решать «обратную задачу»: по данным испытаний оценить ситуацию.

Прямая и обратная задачи

Прямую задачу можно описать так: по причине найти вероятность одного из следствий. Например, дана абсолютно симметричная монета (вероятность выпадения орла, как и решки, равны 1/2). Нужно посчитать вероятность того, что если мы дважды подкинем монету, оба раза выпадет орел. Очевидно, что она равна 1/2 * 1/2 =1/4.

Но проблема в том, что мы знаем вероятность того или иного события только в меньшинстве случаев, почти все их которых искусственные, например, азартные игры. При этом в природе нет ничего абсолютного, вероятность выпадения орла у реальной монеты равна 1/2 только приблизительно. Можно сказать, что прямая задача изучает некоторых сферических коней в вакууме.

На практике, важнее обратная задача: оценить ситуацию по данным испытаний. Но проблема обратной задачи в том, что ее решение сложнее. Главным образом из-за того, что наше решения будет не точкой P=С, а некоторой функцией P=f(x).

Например, у нас есть монета, нужно оценить с помощью опытов вероятность выпадения решки. Если мы подкинули монету 1 раз и выпал орел, то это не значит, что всегда выпадают орлы. Если 2 раза подкинули и получили 2 орла, то опять это не значит, что выпадают только орлы. Чтобы получить абсолютно точно вероятность выпадения решки, мы должны подкинуть монету бесконечное число раз. На практике это не возможно и мы всегда вычисляем вероятность события с некоторой точностью.

Мы вынуждены использовать некоторую функцию. Обычно ее принято обозначать как P(p=x|s решек, f орлов) и называть плотностью вероятности. Читается это так вероятность, того, что вероятность выпадения орла равна x, если по данным эксперимента выпало s решек и f орлов. Звучит сложно звучит из-за тафтологии. Проще считать p некоторым свойством монетки, а не вероятностью. И читать: так вероятность того, что p=x…

Забегая вперед скажу, что если в первую монетку подкинем 1000 раз и получим 500 орлов, а вторую 10000 и получим 5000 орлов, то плотности вероятности будут выглядеть так:

Из-за того, что у нас не точка, а кривая мы вынуждены использовать доверительные интервалы. Например, если говорят 80% доверительный интервал для p равен 45% до 55%, то это значит с 80% вероятностью p находиться между 45% и 55%.

Биномиальное распределение

Для простоты будем рассматривать биномиальное распределение. Это распределение количества «успехов» в последовательности из некоторого числа независимых случайных экспериментов, таких, что вероятность «успеха» в каждом из них постоянна. Оно наблюдается практически всегда, когда у нас есть последовательность испытаний с двумя возможными исходами. Например, когда мы несколько раз подкидываем монету, или оцениваем CTR банера, или конверсию на сайте.

Для примера будем считать, что нам нужно оценить вероятность выпадения решки у монеты. Мы подкинули монету некоторое число раз и получили f орлов и s решек. Обозначим это событие как [s,f] и подставим это в формулу Байеса вместо B. Событие когда p равно некоторому числу будем обозначать как p=x и подставим вместо события А.

P([s,d]|p=x), Вероятность получить [s,d], если p=x, при условии, что p=x нам известна P([s,f]|p=x)=K(f,s) * x^s (1-x)^f. Где K(f,s) биномиальный коэффициент. Получаем:

Нам неизвестна P([s,f]). Да и биномиальный коэффициент вычислить проблематично: там факториалы. Но эти проблемы можно решить: суммарная вероятность всех возможных x должна быть равна 1.

С помощью простых преобразований мы получим формулу:

Программируется это просто, всего 10 строк:

Однако, у нас остается неизвестной P(p=x). Она выражает, насколько вероятно, что p=x, если данных по эксперименту у нас нет. Эту функцию принято называть априори. Из-за нее и произошел холивар в теории вероятностей. Вычислить априори строго математически мы не можем, только задать субъективно. А без априори мы не можем решить обратную задачу.

Холивар

Сторонники классической интерпретации (частотного подхода, ЧП), считают, что все возможные p равновероятны до начала эксперимента. Т.е. перед экспериментом нужно «забыть» те данные, которые нам известны до него. Их оппоненты, сторонники байесовского подхода (БП), считают, что нужно задать какую-то априори исходя из наших знаний до начала эксперимента. Это фундаментальное отличия, даже определение понятия вероятности у этих групп разное.

Кстати, создатель этой формулы, Томас Баейс умер лет на 200 раньше холивара и отношение к этому спору имеет только косвенное. Формула Байеса часть обоих конкурирующих теорий.

Частотный подход(ЧП) лучше подходит для науки, где нужно объективно доказать какую-то гипотезу. Например, то что смертность от препарата меньше определенного порога. Если же вам нужно, учитывая всю доступную информацию, принять решение, то лучше использовать БП.

ЧП не подходит для прогнозирования. Кстати, формулы доверительных интервалов, считают доверительные интервал по ЧП. Сторонники БП, обычно, в качестве априори для биномиального распределения используют Бета распределение, при a=1 и b=1 оно вырождается в непрерывное распределение, которое используют их противники. В итоге формула принимает вид:

Это универсальная формула. При использовании ЧП нужно задать b=a=1. Сторонники БП некоторым образом должны выбрать эти параметры, так чтобы получилось правдоподобное бета-распределение. Зная a и b можно использовать формулы ЧП, например для расчета доверительного интервала. Например, мы выбрали a=4.5, b=20, у нас есть 50 успехов и 100 неудач, чтобы вычислить доверительный интервал в БП нам нужно в обычную формулу ввести 53.5 (50+4.5-1) успеха и 119 неудачу.

Однако, у нас нет никаких критериев выбора a и b. Следующая глава расскажет как их выбрать по статическим данным.

Прогноз

Логичнее всего в качестве прогноза использовать мат. ожидание. Его формулу легко получить из формулы мат. ожидания бета-рапределения. Получим:

.

Например, у нас есть сайт, со статьями. На каждой из них есть кнопка «лайк». Если мы будем сортировать по числу лайков, то у новых статей мало шансов перебить старых. Если мы будем сортировать по соотношению лайков к посещениям, то статьи с одном заходом и одним лайком будут перебивать статью с 1000 заходами и с 999 лайками. Разумнее всего сортировать по последней формуле, но нужно каким-то образом определить a и b. Самый простой способ через 2 основных момента бета-распределения: мат. ожидание (сколько в среднем будет) и дисперсию (каково в среднем отклонение от среднего).

Пусть L средняя вероятность лайка. Из матожидания бета-распределения L=a/(a+b) =>a+b=a/L=> aL+bL=a => b=a(1/L — 1). Подставим в формулу дисперсии:

На псевдокоде это будет выглядеть так:

Не смотря на то, что данный выбор a и b кажется объективным. Это не строгая математика. Прежде всего не факт, что лайкабельность статей подвержена Бета-распределению, в отличии от биномиального это распределение «не физично», оно введено для удобства. Мы по сути подогнали кривую к статистическим данным. Причем вариантов подгонки есть несколько.

Шанс побить всех

Например, мы провели А/B тест нескольких вариантов дизайна сайта. Получили некоторые результаты и думаем, нужно ли его останавливать. Если мы остановимся слишком рано мы можем выбрать не верный вариант, но остановиться когда-то все-таки нужно. Мы можем оценивать доверительные интервалы, но их анализ сложен. Как минимум, поскольку в зависимости от коэффициента значимости у нас получаются разные доверительные интервалы. Сейчас я покажу как посчитать вероятность того, что один вариант лучше всех остальных.

Кроме зависимых событий существуют и независимые события. Для таких событий P(A|B)=P(A). Поэтому P(AB)=P(B)P(A|B)=P(A)P(B). Для начала нужно показать что варианты независимы. Кстати сравнивать доверительные интервалы корректно, только в случае когда варианты независимы. Как уже было сказано, сторонники ЧП отбрасывают все данные кроме самого эксперимента. Варианты это отдельные эксперименты, поэтому каждый из них зависит только от своих результатов. Поэтому они независимы.

Для БП доказательство сложнее, основной момент, что априори «изолирует» варианты друг от друга. Например, события «голубые глаза» и «знает арабский» зависимы, а события «араб знает арабский» и «у араба голубые глаза» нет, поскольку взаимосвязь между первыми двумя событиями исчерпывается событием «человек араб». Более верная запись P(p=x) в нашем случае следующая: P(p=x|apriori=f(x)). Поскольку все зависит от выбора функции априори. А события P(p_i=x|apriori=f(x)) и P(p_j=x|apriori=f(x)) независимы, поскольку единственная взаимосвязь между ними это функция априори.

Источник

Математическая статистика

Интервальные оценки

Понятие доверительного интервала

Пусть X₁,…,X_n – случайная выборка объёма n из генеральной совокупности X с функцией распределения F_X(x; θ), зависящей от параметра θ, значение которого неизвестно. Доверительным интервалом для параметра θ называется интервал (θ₁; θ₂), содержащий (накрывающий) истинное значение θ с заданной вероятностью γ, т.е.

Доверительный интервал – это интервал со случайными границами θ₁ и θ₂. Для каждой новой реализации x₁,…,x_n случайной выборки X₁,…,X_n эти случайные величины, а следовательно, и случайные величины θ₁, θ₂ будут принимать новые значения. Однако, согласно определению, для данной реализации x₁,…,x_n рассчитанная реализация доверительного интервала (θ₁; θ₂) накроет истинное значение неизвестного параметра θ с заданной вероятностью γ. Это означает, что доля реализаций случайной выборки X₁,…,X_n, для которых доверительный интервал (θ₁; θ₂) накроет θ, в среднем равна доверительной вероятности γ.

Пример. Исследуется качество партии выпускаемых предприятием изделий. Пусть θ – доля бракованных изделий в партии, которую оценивают независимо друг от друга в N различных лабораториях по результатам обследования нескольких случайно выбранных деталей из партии. Иначе говоря, долю бракованных изделий в партии в каждой лаборатории оценивают по «своей» выборке деталей из партии, и в каждой лаборатории получают свои значения верхней и нижней границ γ-доверительного интервала.

Ширина доверительного интервала, характеризующая точность интервального оценивания, зависит от объёма выборки n и доверительной вероятности γ: при увеличении объёма выборки ширина доверительного интервала уменьшается. Причина этого состоит в том, что в выборке большего объёма содержится больше информации об оцениваемом параметре, что позволяет более точно определить область, в которой он находится. При увеличении доверительной вероятности предъявляется более «жёсткое» требование к вероятности нахождения неизвестного параметра внутри доверительного интервала, вследствие чего его ширина увеличивается.

Границы доверительного интервала θ₁ и θ₂ могут быть выбраны множеством способов. Единственное требование, предъявляемое к этим статистикам – это выполнение условия (1). Однако на практике, как правило, эти статистики выбирают, исходя из некоторых соображений симметрии, которые будут рассмотрены далее.

Иногда требуется оценить параметр θ только снизу или только сверху. При этом, если

Источник

Доверительный интервал

Доверительный интервал — термин, используемый в математической статистике при интервальной (в отличие от точечной) оценке статистических параметров, что предпочтительнее при небольшом объёме выборки. Доверительным называют интервал, который покрывает неизвестный параметр с заданной надёжностью.

Содержание

Определение

.

Граничные точки доверительного интервала и называются доверительными пределами.

Интерпретация доверительного интервала, основанная на интуиции, будет следующей: если p велико (скажем, 0,95 или 0,99), то доверительный интервал почти наверняка содержит истинное значение θ. [ссылка 2]

Еще одно истолкование понятию доверительного интервала: его можно рассматривать как интервал значений параметра θ, совместимых с опытными данными и не противоречащих им.

Примеры

Байесовский доверительный интервал

В байесовской статистике существует схожее, но отличающееся в некоторых ключевых деталях определение доверительного интервала. Здесь оцениваемый параметр сам считается случайной величиной с некоторым заданным априорным распределением (в простейшем случае — равномерным), а выборка фиксирована (в классической статистике всё в точности наоборот). Байесовский -доверительным интервал — это интервал , покрывающий значение параметра с апостериорной вероятностью :

.

Как правило, классический и байесовский доверительные интервалы различаются. В англоязычной литературе байесовский доверительный интервал принято называть термином credible interval, а классический — confidence interval.

Примечания

Полезное

Смотреть что такое «Доверительный интервал» в других словарях:

Доверительный интервал — интервал, вычисленный по выборочным данным, который с заданной вероятностью (доверительной) накрывает неизвестное истинное значение оцениваемого параметра распределения. Источник: ГОСТ 20522 96: Грунты. Методы статистической обработки результатов … Словарь-справочник терминов нормативно-технической документации

доверительный интервал — для скалярного параметра генеральной совокупности – это отрезок, с большой вероятностью содержащий этот параметр. Эта фраза без дальнейших уточнений бессмысленна. Поскольку границы доверительного интервала оцениваются по выборке, естественна его… … Словарь социологической статистики

ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ — (confidence interval) Интервал, в котором достоверность значения параметра по населению, полученного на основе выборочного обследования, имеет определенную степень вероятности, например 95%, что обусловлено самой выборкой (sample). Ширина… … Экономический словарь

доверительный интервал — – интервал, в котором находится истинное значение определяемой величины с заданной доверительной вероятностью. Общая химия : учебник / А. В. Жолнин [1] … Химические термины

Доверительный интервал ДИ — Доверительный интервал, ДИ * давяральны інтэрвал, ДІ * confidence interval интервал значения признака, рассчитанный для к. л. параметра распределения (напр., среднего значения признака) по выборке и с определенной вероятностью (напр., 95% для 95% … Генетика. Энциклопедический словарь

ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ — понятие, возникающее при оценке параметра статистич. распределения интервалом значений. Д. и. для параметра q, соответствующий данному коэф. доверия Р, равен такому интервалу (q1, q2), что при любом распределении вероятности неравенства… … Физическая энциклопедия

доверительный интервал — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN confidence interval … Справочник технического переводчика

доверительный интервал — pasikliovimo intervalas statusas T sritis Standartizacija ir metrologija apibrėžtis Dydžio verčių intervalas, kuriame su pasirinktąja tikimybe yra matavimo rezultato vertė. atitikmenys: angl. confidence interval vok. Vertrauensbereich, m rus.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

доверительный интервал — pasikliovimo intervalas statusas T sritis chemija apibrėžtis Dydžio verčių intervalas, kuriame su pasirinktąja tikimybe yra matavimo rezultatų vertė. atitikmenys: angl. confidence interval rus. доверительная область; доверительный интервал … Chemijos terminų aiškinamasis žodynas

Источник