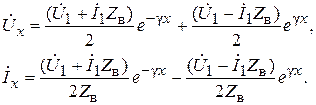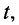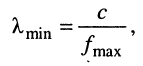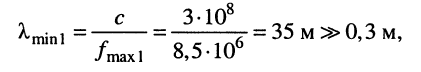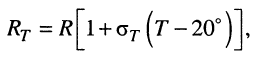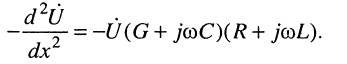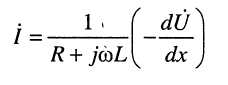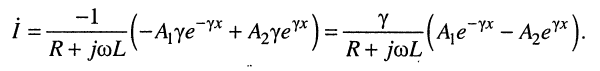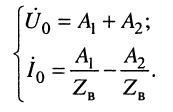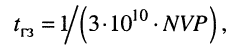понятие о цепях с распределенными параметрами

ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

Общие сведения

Цепями с распределенными параметрами называются идеализированные электрические цепи, процессы в которых описываются дифференциальными уравнениями в частных производных. Это связано с тем, что если длина волны λ электромагнитных колебаний соизмерима с размерами цепи l, то токи и напряжения в этой одномерной цепи являются функциями двух переменных – времени t и координаты x – u(t, x), i(t, x).

Исторически первыми в качестве одномерных цепей с распределенными параметрами стали представлять так называемые длинные линии, т.е. двухпроводные линии передачи сигнала от источника к нагрузке (рис. 6. 1), длина которых l значительно превышает длину волны λ передаваемых электромагнитных колебаний. Поэтому часто эти цепи называют длинными линиями или линиями. При этом будем полагать, что конструктивные данные линии (материал и диаметр ее проводов, их взаимное расположение) и ее параметры сохраняются неизменными по длине линии. Такие длинные линии называются однородными.

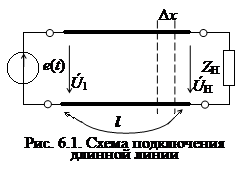
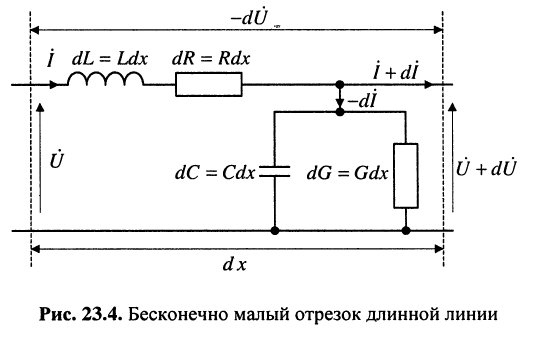
Задача анализа цепей с распределенными параметрами обычно сводится к определению законов (характера) изменения токов и напряжений вдоль цепи и к исследованию частотных и временных характеристик цепи. С этой целью следует рассмотреть электрическую модель отрезка линии малой длины Δx = dx. Эта модель с достаточной точностью исследования может быть представлена электрической цепью с сосредоточенными параметрами (рис. 6.2). Всю линию можно представить как цепи с бесконечно большим числом малых по величине пассивных элементов, распределенных равномерно по ее длине.

На основании физических рассуждений можно составить следующую эквивалентную схему отрезка (рис. 6.2).

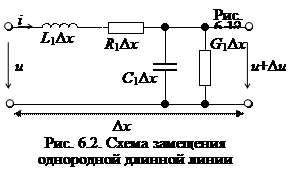
При прохождении тока вокруг проводника образуется внешнее магнитное поле, которое можно моделировать индуктивностью L₀. Она препятствует прохождению тока. Вместе с этим проводник обладает сопротивлением материала R₀. Следовательно, эти элементы должны быть соединены последовательно.

Проводники объединены конструктивно диэлектриком, который обладает конечной резистивной проводимостью G₀. Между проводниками линии создается разность потенциалов. Следовательно, вокруг проводников существует электрическое поле, накопление которого моделируется емкостью С₀.

Элементы L₀, C₀, R₀, G₀ называются параметрами линии (отрезка линии). Однако каждый отрезок линии имеет конечную длину Dx, поэтому вводятся понятия погонных параметров:

Входное сопротивление линии

Входное сопротивление линии определяется отношением напряжения и тока в начале линии. Найдем выражение входного сопротивления

используя уравнения (6.11)

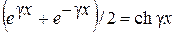
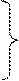
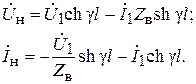
Если учесть, что и и принять при x = l Ú_x = Ú_н и Ì_x = Ì_н, то система уравнений (6.11) примет вид

(6.28)

Разрешая эту систему уравнений относительно напряжения Ú₁ и тока Ì₁, получим

(6.29)

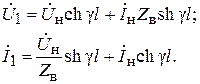
Используя уравнения (6.29), получим выражение входного сопротивления

(6.30)

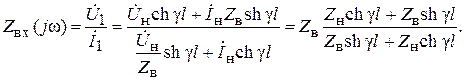
Рассмотрим некоторые частные режимы работы линии.

1. При согласованном включении линии (Z_н = Z_в) из (6.30) получим, что

2. Если выходные зажимы линии замкнуты накоротко (Z_н = 0), то формула (6.30) упрощается:

(6.31)

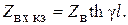
3. В случае разомкнутых выходных зажимов (Z_н = ∞)

(6.32)

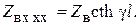
4. Когда линия нагружена на произвольное сопротивление, не равное волновому (Z_н ≠ Z_в), можно пользоваться для расчетов не только формулой (6.30), но и более удобной. Для этого разделим числитель и знаменатель в (6.30) на ch γl:

.

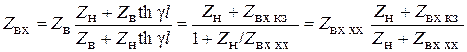
Линия без потерь

Вторичные параметры и уравнения передачи. Реальная линия всегда обладает потерями. Однако в ряде случаев удобно считать линию идеальной, т. е. не имеющей потерь: R₁ = G₁ = 0. Такая идеализация оправдана для коротких по длине линий, работающих на сверхвысоких частотах (фидеров, элементов радиотехнических устройств, полосковых линий и др.), где выполняются условия R₁ 0 амплитуды убывают в сторону нагрузки). Сдвиг фаз между напряжением u_x и током i_x равен нулю, поэтому энергия бегущей волны носит активный характер. Следовательно, в режиме бегущих волн передача энергии в линии производится только в одном направлении – от источника энергии к нагрузке. Вся энергия, предаваемая падающей волной, потребляется нагрузкой. Этот режим используется для передачи сигнала от источника в нагрузку.

Входное сопротивление из (6.35) равно волновому сопротивлению Z_ВХ = R₀.

Режим стоячих волн. Как было сказано ранее, что если модуль коэффициента отражения линии │p(x)│ ≡ 1, т. е. амплитуды отраженной и падающей волн во всех сечениях линии одинаковы, то в линии устанавливается специфический режим, называемый режимом стоячих волн. Это равенство амплитуд возможно только в линии без потерь (α = 0) т. е. │p_н│ = 1.

Анализируя выражение (6.23) 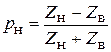, можно убедиться, что │p_н│ = 1 только в трех случаях: Z_н = 0, либо Z_н = ∞, либо Z_н = jx.

Следовательно, режим стоячих волн может установиться только в линии без потерь при коротком замыкании или холостом ходе на выходе, а также если сопротивление нагрузки имеет чисто реактивный характер.

Короткое замыкание линии КЗ. При Z_н = 0 напряжение в конце линии равно нулю Ú_н = 0. Уравнения передачи (6.34) для данного режима принимают вид:

(6.36)

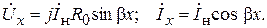
Если положить для простоты начальную фазу тока в конце линии равной нулю φi_н = 0, то мгновенные значения напряжения и тока в любой точке линии описываются выражениями:

(6.37)

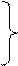
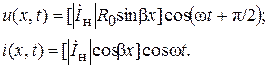
Выражения (6.37) показывают, что при коротком замыкании на выходе линии амплитуды напряжения и тока изменяются вдоль линии по периодическому (гармоническому) закону

,

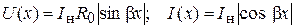
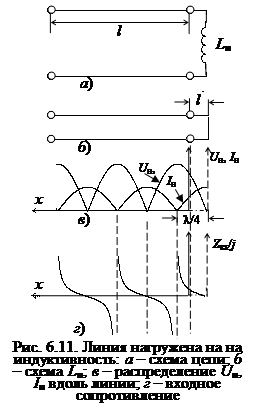
принимая в отдельных точках линии максимальные значения U_max =R₀I_н, I_н = I_max и обращаются в нуль в некоторых других точках (рис. 6.6).

Точки, в которых амплитуда (мгновенные значения) напряжения (тока) тождественно равны нулю, называются узлами напряжения (тока).

Характерные точки, в которых амплитуда (мгновенные значения) напряжения (тока) принимают максимальное значение, называются пучностями напряжения (тока). Как видно из рис. 6.6, узлы напряжения соответствуют пучностям тока и, наоборот, узлы тока соответствуют пучностям напряжения.

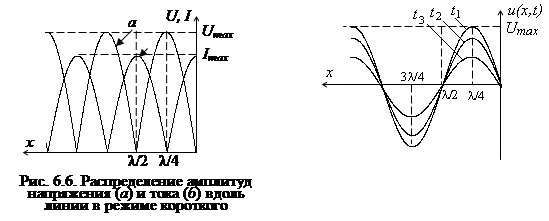Распределение мгновенных значений напряжения (рис. 6.7) (тока) вдоль линии гармоническому закону, однако с течением времени координаты точек, имеющих одинаковую фазу, остаются неизменными, т. е. волны напряжения (тока) как бы «стоят на месте». Именно поэтому такой режим работы линии получил название режима стоячих волн.

Координаты узлов напряжения определяются из условия sinβx_k = 0, откуда при β = 2π/π

где k = 0, 1, 2, …, а координаты пучностей напряжения – из условия cosβx_k = 0, откуда

Пучности возникают в тех сечениях линии, в которых падающая и отраженная волны напряжения (тока) совпадают по фазе и, следовательно, суммируются, а узлы располагаются в сечениях, где падающая и отраженная волны напряжения (тока) находятся в противофазе и, следовательно, вычитаются.

Мгновенная мощность в узлах напряжения и тока в любой момент времени равна нулю.

Таким образом, в режиме стоячих волн энергия вдоль линии не распространяется и на каждом участке линии происходит только обмен энергией между электрическим и магнитным полями. Этот режим не используется для передачи сигнала от источника в нагрузку.

Из (6.36) следует, что входное сопротивление в произвольной точке x линии равно (расстояние x от конца линии)

(6.38)

Из выражения (6.38) следует, что резистивная составляющая комплексного входного сопротивления отрезка линии без потерь а режиме КЗ на выходе равна нулю, а реактивная составляющая

является периодической функцией электрической длины x/λ и может принимать любые значения от – ∞ до ∞ (рис. 6.8).

При x = 0, λ/2, λ, 3λ/2, … величина βx = (2π/λ)x = 0, π, 2π, 3π, … и входное сопротивление Z_{вх кз} = 0. При x = λ/4, 3λ/4, 5λ/4, … величина βx = (2π/λ)x = π/2. и входное сопротивление Z_{вх кз} = ±j∞.

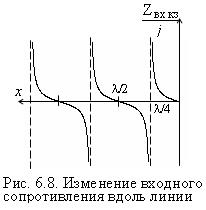
В случае, когда линия нагружена на емкость C_н можно поступить так же, как при индуктивной нагрузке.

Включение линии на произвольное комплексное сопротивление, не равное волновому. Положим для определенности, что сопротивление нагрузки R_н>R₀. Коэффициент отражения на основании (6.23)│p│=(R_н–R₀)/(R_н+R₀)

Источник

Понятие об электрических цепях с распределенными параметрами

ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

Понятие об электрических цепях с распределенными параметрами

Строго говоря, всегда параметры электрической цепи в той или иной степени распределены вдоль ее участков, и только абстрагируясь от действительности можно предполагать, что такие параметры цепи как активное сопротивление – R, индуктивность – L и емкость – C сосредоточены в ее определенных участках. Во многих случаях такое допущение не приводит к существенным ошибкам в результатах проводимого анализа. Ранее мы имели дело с цепями с сосредоточенными параметрами. Однако, такой подход не всегда возможен. Например, рассматривая электромагнитные процессы, происходящие в электрических линиях, при помощи которых электрическая энергия или сигналы передаются на расстояние, необходимо иметь ввиду, что электрические и магнитные поля распределены по всей длине линии, и превращение электрической энергии в тепло также происходит по всей длине линии. Критерием необходимости рассматривать цепь в качестве цепи с распределенными параметрами является то, что интервал времени распространения электромагнитной волны вдоль всей цепи и интервал времени, в течение которого токи и напряжения меняются на заметную величину, должны быть соизмеримыми.

Токи напряжения в таких цепях являются функциями двух независимых переменных: времени – t и расстояния – x, отсчитываемого вдоль направления цепи. Уравнения, описывающие процессы в таких цепях, являются уравнениями в частных производных. Примерами являются линии передачи электрической энергии, линии связи, антенные вводы радиотехнических устройств, обмотки электрических машин при воздействии на них импульсных токов и напряжений.

Параметры цепи могут быть распределены неравномерно вдоль линии.

Однако во многих случаях этим можно пренебречь и считать параметры равномерно распределенными. Такие линии называются однородными.

В дальнейшем под величинами R, L, C, G, M будем понимать активное сопротивление, индуктивность и т.д., приходящиеся на единицу длины, и будем обозначать их через R₀, L₀, C₀, G₀, M₀. В общем случае эти параметры зависят от частоты, например, увеличение активного сопротивления и индуктивности с ростом частоты вследствие поверхностного эффекта. Однако для простоты в дальнейшем это учитывать не будем.

Источник

Цепи с распределёнными параметрами

Содержание:

Цепи с распределёнными параметрами:

Во всех предыдущих лекциях изучались электрические цепи с сосредоточенными параметрами, т. е. такие цепи, модели которых содержат конечное число элементов R, L и С (см. разд. 1.3). Геометрические размеры таких цепей и входящих в них элементов не имеют никакого значения, поскольку электрическая и магнитная энергии локализованы в конденсаторах и катушках индуктивности соответственно, а потери мощности приходятся на резисторы.

Однако не всякую электрическую цепь можно описать с помощью сосредоточенных параметров. Например, для направленной пространственной передачи электромагнитной энергии от одного радиотехнического устройства к другому используются электрические цепи, представляющие собой пары проводников той или иной конструкции, разделённые каким-либо диэлектриком. В таких цепях отсутствуют пространственные области с преимущественной локализацией электрического или магнитного полей. Модель подобной электрической цепи должна содержать бесконечное число бесконечно малых по величине пассивных элементов. Иначе говоря, в такой цепи имеет место распределённые по всей её длине индуктивности, ёмкости и активные сопротивления. По этой причине такие цепи называются цепями с распределёнными параметрами.

Среди цепей с распределёнными параметрами особая роль в технике связи принадлежит длинным линиям, изучению которых посвящена данная глава.

Первичные параметры длинной линии

Распределённый характер элементов и конечная скорость распространения электромагнитной энергии означает, что в линии напряжения и токи являются функциями не только времени

Зависимость токов и напряжений в линии от пространственных координат является тем основным признаком, который отличает длинные линии от других устройств системы связи.

Понятие длинной линии

Определение длинной линии:

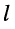
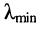
Для более, чёткого определения длинной линии вводят количественный критерий, связанный с соотношением между длиной самой линии, измеряемой в метрах (в радиосистемах) или километрах (в многоканальных системах связи), и минимальной длиной волны гармонических составляющих воздействия.

Этот критерий часто называют электрической длиной. С помощью этого критерия нетрудно определить, является ли в конкретных обстоятельствах исследуемая линия длинной или она может рассматриваться как система с сосредоточенными параметрами. Суть критерия состоит в следующем.

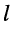
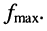
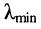
Пусть к линии длиной приложено воздействие, максимальная частота гармонических составляющих которого равна Тогда минимальная длина волны определится из известной формулы

где 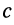— скорость света.

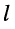
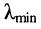
Рассмотрим два варианта соотношений между и :

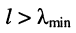
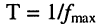
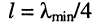
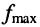
1. Длина линии / превышает или имеет один порядок с минимальной длиной волны A.mjn. Это означает, что на линии длиной укладывается более одного периода заданной гармоники. Если длина линии и длина волны имеют один порядок, т. е. их длины соизмеримы, на линии укладывается существенная часть одного периода, по которой можно полностью определить параметры гармонического колебания. Наименьшей существенной частью периода является его четверть. Тогда, например, на линии длиной укладывается ровно четверть периода заданного гармонического колебания (такая линия называется четвертьволновым отрезком и широко применяется на практике). Следовательно, и в том и в другом случае колебание с частотой будет иметь различную фазу в разных точках линии и потому запаздывать относительно изменения мгновенного значения напряжения или тока на входе линии. Иначе говоря, в один и тот же момент времени мгновенные значения токов и напряжений в различных точках линии будут различными. Такая линия и является длинной. Отмеченное запаздывание играет существенную роль при передаче сигналов и будет изучено в дальнейшем.

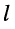
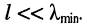
2. Длина линии существенно меньше минимальной длины волны . Тогда во всех точках линии колебания всех гармонических составляющих воздействия находятся практически в фазе, поэтому токи и напряжения не зависят от пространственных координат. Такая линия не является длинной, она считается системой с сосредоточенными параметрами и может быть заменена эквивалентной ей цепью из элементов R, L и С.

Пример 23.1.

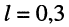
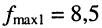
Имеется отрезок кабеля длиной м. Определить его принадлежность к длинной линии или к цепи с сосредоточенными параметрами, если по нему передаётся телевизионный сигнал в одном случае с наивысшей частотой МГц, а в другом — в диапазоне дециметровых волн (частоты 300—3000 МГц).

Решение. Минимальная длина волны в первом случае составляет

поэтому данный отрезок кабеля может считаться цепью с сосредоточенными параметрами.

Во втором случае, когда длина волны 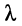не превышает десятков сантиметров, этот же отрезок кабеля должен рассматриваться как длинная линия.

Отсюда следует смысл критерия электрической длины линии:

одна и та же цепь представляет собой систему с распределёнными или сосредоточенными параметрами в зависимости от частоты приложенного к ней воздействия.

В приведённом примере демонстрировался случай распространения высокочастотного колебания в отрезке кабеля. С другой стороны, для излучения радиоволн требуется разместить в пространстве систему проводников и подвести к ней колебания от радиопередатчика. Такая система называется антенной. Из критерия электрической длины следует ясное правило: чтобы антенна хорошо излучала, её размеры должны быть сравнимы с длиной излучаемой волны. Невозможно, например, излучать километровые волны с помощью небольшого куска проволоки. По этой причине длинноволновые передающие антенны (так называемые антенные поля) имеют гигантские размеры, измеряемые в километрах. Если же передатчик работает в диапазоне дециметровых волн, размеры передающей антенны не превосходят нескольких метров и антенна может представлять собой штырь. Например, радиостанция «Кварц», работающая в диапазоне 1,5—7 МГц, имеет штыревую антенну длиной 1,5 м, а радиостанция Р-163-10К работает в диапазоне 2— 30 МГц и среди других антенн имеет антенну-штырь 2,4 м.

Задача анализа процессов распространения электромагнитной энергии в длинных линиях достаточно сложна. Она является частной задачей анализа процессов распространения электромагнитной энергии в неоднородных средах. Такие задачи решаются с помощью уравнений Максвелла, однако непосредственное применение уравнений Максвелла для подобных задач весьма затруднительно и выполнимо лишь при некоторых ограничениях, или допущениях, когда решения получаются особенно простыми, что показано в разд. 23.3.

Кроме того, поскольку в длинных линиях мгновенные значения тока и напряжения в различных точках различны, к ним не применимы законы Ома и Кирхгофа. Тем не менее, к длинным линиям можно применять теорию электрических цепей и, в частности, теорию четырёхполюсников, если принять следующие основные допущения о длинных линиях:

Классификация длинных линий

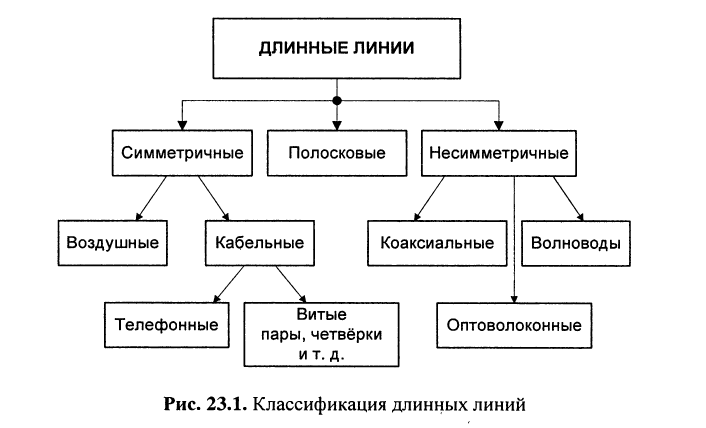
Длинные линии классифицируются, в основном, по конструктивным признакам (рис. 23.1), которые определяют электрические свойства линии.

В настоящее время принята следующая классификация длинных линий:

Более подробная классификация кабелей согласно принятым международным стандартам приведена в разд. 23.4.

Первичные параметры длинной линии

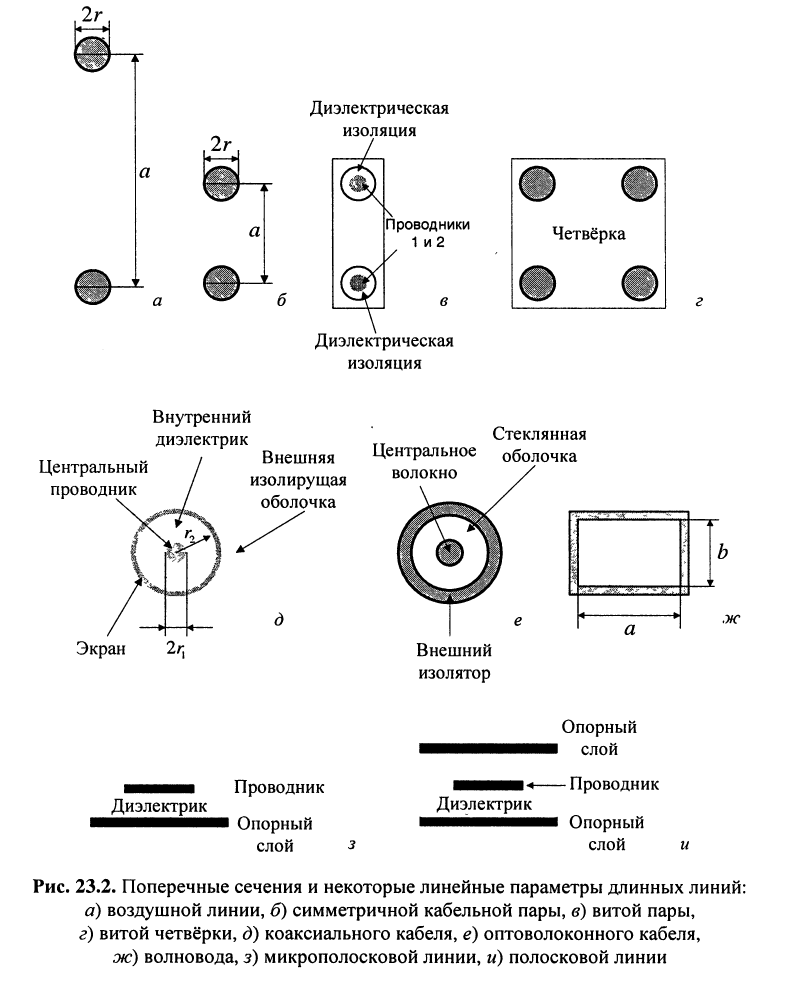
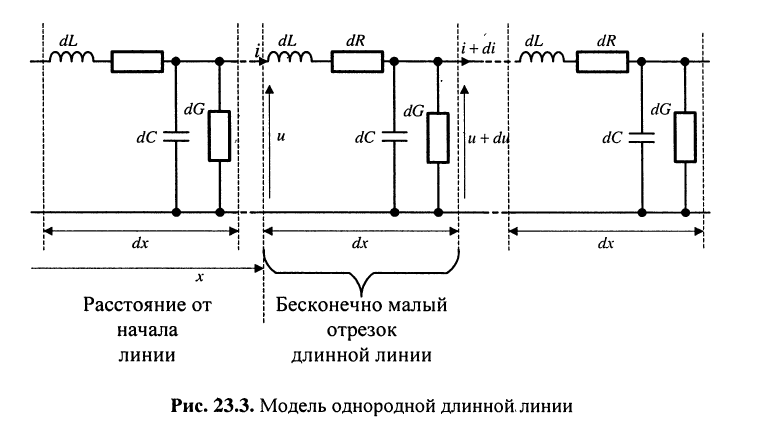
Согласно принятым допущениям о длинных линиях однородная линия может быть представлена своей моделью в виде цепи с бесконечно большим числом бесконечно малых по величине пассивных элементов (рис. 23.3), равномерно расположенных по её длине.

Измерить и вычислить эти величины невозможно; тем не менее, знать электрические характеристики линии необходимо. Электрические характеристики линии оценивают через её параметры, которые разделяют на две группы: первичные и вторичные параметры.

Первичные параметры линии характеризуют её физическую природу и выражаются через сопротивление, индуктивность, ёмкость, проводимость, отнесённые к единице длины линии (1 км в линиях проводной связи и 1 м в линиях радиосвязи). По этой причине первичные параметры называют также погонными.

Следовательно, погонными параметрами являются:

В оптоволоконных кабелях первичным параметром является зависимость коэффициента преломления оптического волокна от расстояния до оптической оси.

Вторичные параметры, изучаемые в разд. 23.3, характеризуют отклик линии передачи на некоторые эталонные воздействия, в качестве которых наиболее часто используются гармонические сигналы различных частот.

Рассмотрим первичные параметры подробнее. В табл. 23.1 без доказательства приводятся расчётные формулы первичных параметров, вывод которых осуществляется методами теории электромагнитного поля, из которой известно, что плотность тока в уединённом проводе круглого сечения неравномерна и убывает от поверхности к центру провода. Скорость убывания тем больше, чем выше частота. 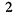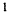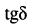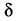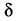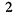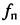Это явление известно под названием поверхностного эффекта, или скин-эффекта.

— тангенс угла диэлектрических потерь (или просто тангенс угла потерь); угол представляет собой дополняющий до 90° угол между приложенными напряжением и током, протекающим через конденсатор с данным диэлектриком. Тангенс угла потерь используется для определения затухания в линии, вызываемого диэлектрическими потерями вследствие неидеальности диэлектрика.

В основе поверхностного эффекта лежит индукционный механизм, обусловленный скоростью изменения магнитных полей в проводнике, поэтому эффект нарастает с ростом частоты. Выше некоторой пороговой частоты поверхностный эффект «выталкивает» ток в более тонкий слой по периметру проводника, что вызывает неограниченный рост кажущегося активного сопротивления, которое возрастает пропорционально корню квадратному частоты.

Неравномерность распределения плотности тока по сечению провода эквивалентна уменьшению площади его поперечного сечения и, следовательно, увеличению сопротивления провода с ростом частоты. В то же время скин-эффект уменьшает внутреннюю индуктивность при возрастании частоты. По этой причине в технике связи используются кабели разнообразной конструкции, отличающиеся способностью эффективно передавать сигналы различных частотных диапазонов (см. разд. 23.4).

Сопротивление R проводов при температурах, отличных от 20°, уточняется по формуле

где 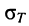[1/град] — температурный коэффициент, Т — температура С°. Сопротивление растёт пропорционально квадратному корню из частоты колебания.

Индуктивность L определяется отношением магнитного потока, сцепляющегося с контуром единичной длины, к току, вызывающему этот поток. Индуктивность линии складывается из внешней и внутренней индуктивностей. Внешняя индуктивность определяется только геометрическими размерами линии и не зависит от частоты. Внутренняя индуктивность зависит от материала проводов, их диаметра и частоты. Скин-эффект уменьшает внутреннюю индуктивность с ростом частоты.

Ёмкость С определяется отношением заряда, приходящегося на единицу длины линии, к напряжению между проводами линии; ёмкость от частоты практически не зависит.

Проводимость G обусловлена потерями в диэлектрике и зависит от частоты: с ростом частоты проводимость увеличивается.

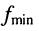
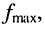
Любая линия обладает некоторой рабочей полосой частот от до на которых частотно зависимые первичные параметры имеют различные значения, поэтому при анализе колебаний в линии полагают численные значения первичных параметров линии равными их средним значениям в рабочей полосе.

Теперь можно уточнить определение однородной линии, введённое в качестве первого допущения о длинных линиях.

Определение:

Однородной линией называется такая линия, первичные параметры которой неизменны по всей длине.

Линию с неравномерным распределением первичных параметров часто можно разбить на однородные участки.

Уравнения передачи длинной линии

Постановка задачи. Как было отмечено, напряжения и токи в длинной линии являются функциями времени t и координаты х, отсчитываемой от одного из концов линии. Этот факт значительно усложняет анализ распределения напряжения и тока для колебания произвольной формы. Дело существенно упрощается, если воспользоваться режимом установившихся гармонических колебаний, поскольку для этого режима заранее известен закон изменения напряжений и токов от времени в любом сечении линии. С другой стороны, для длинных линий, в силу распределённости её параметров по всей длине, неприменимы законы Ома и Кирхгофа. Если же длинную линию представить как цепь с бесконечно большим числом бесконечно малых по величине пассивных элементов (см. рис. 23.3), то в цепи можно выделить бесконечно большое число бесконечно малых отрезков и каждый из них рассматривать как четырёхполюсник, находящийся на расстоянии 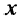от начала линии. Параметры каждого четырёхполюсника бесконечно малы. Для такого отрезка длинной линии применимы законы Ома и Кирхгофа.

Задача 23.1.

Найти законы изменения напряжения и тока вдоль однородной линии в режиме установившихся гармонических колебаний.

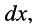
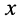
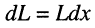
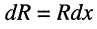
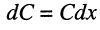
Решение. Выделим бесконечно малый отрезок длинной линии находящийся на расстоянии от её начала (рис. 23.4.). На таком участке можно положить, что токи являются квазистационарными и его эквивалентная схема содержит сосредоточенные параметры: последовательно включённые индуктивность и сопротивление и параллельно включённые ёмкость и активную проводимость

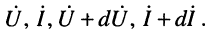
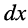
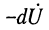
Воспользуемся символическим методом анализа гармонических колебаний, для чего обозначим комплексные напряжения и токи в начале и в конце отрезка как К данному отрезку длинной линии, представляющему собой четырёхполюсник с сосредоточенными параметрами, можно применить законы Ома и Кирхгофа. Тогда при выбранных направлениях отсчёта согласно законам Кирхгофа падение напряжения на отрезке составит , а ток в поперечной проводимости равен

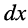
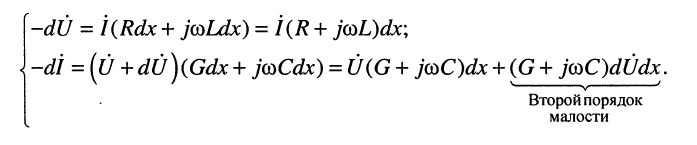
Для указанных напряжения и тока на отрезке можно по закону Ома записать пару уравнений:

(23.1)

Второй порядок малости

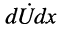
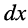
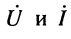
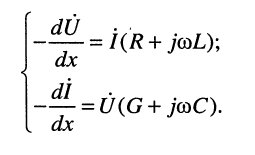
Второе слагаемое в уравнении (23.1) содержит произведение и потому является величиной более высокого порядка малости по сравнению с первым слагаемым. По этой причине вторым слагаемым можно пренебречь. Разделив далее оба уравнения на , получаем систему дифференциальных уравнений с неизвестными :

(23.2)

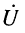
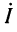
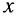
Уравнения (23.2) называются телеграфными, т. к. впервые были получены для линий телеграфной связи. В этих уравнениях и представляют собой комплексные амплитуды напряжения и тока в сечении линии, удалённом на расстояние от начала линии.

Чтобы получить законы изменения напряжений и токов гармонических колебаний, необходимо решить дифференциальные уравнения (23.2).

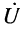
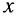
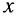
Найдём комплексное напряжение в сечении на расстоянии от начала линии. Для этого продифференцируем первое уравнение из (23.2) по :

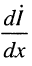
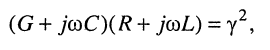
и подставим сюда выражение для из второго уравнения (23.2):

(23.3)

получаем однородное дифференциальное уравнение второго порядка с постоянными коэффициентами

(23.4)

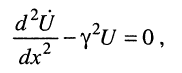
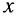
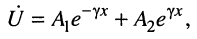
общее решение которого для напряжения в точке , как известно, имеет вид:

(23.5)

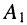
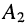
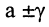
где и — постоянные интегрирования, — корни характеристического уравнения

Теперь нетрудно найти общее решение для распределения тока 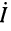в линии, если из первого уравнения (23.2) записать

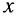
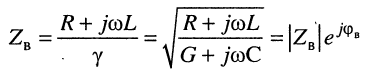
и подставить сюда результат дифференцирования по уравнения (23.5):

(23.6)

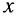
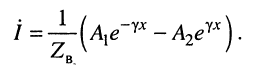
называется волновым сопротивлением длинной линии. При использовании (23.26) решение для тока в точке примет вид:

(23.7)

Пара уравнений (23.5) и (23.7) составляет общее решение телеграфных уравнений (23.2) для напряжения и тока в точке :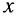

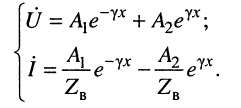
(23.8)

Таким образом, поставленная задача решена: получены уравнения передачи длинной линии (23.8).

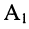
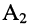
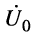
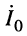
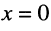
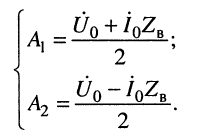
Постоянные интегрирования и зависят только от значений напряжений и токов на внешних зажимах линии и , т. е. от начальных условий. Следовательно, при из (23.8) получаем:

(23.9)

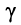
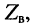
Параметры и называемые соответственно коэффициентом распространения и волновым сопротивлением, относятся к вторичным параметрам длинной линии и зависят исключительно от свойств линии и частоты гармонических колебаний и не меняются при изменении начальных условий.

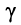
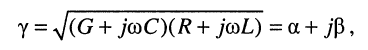
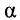
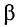
Коэффициент распространения в общем случае является комплексной величиной и записывается в виде:

(23.10)

— коэффициент затухания;

— коэффициент фазы.

Физический смысл указанных параметров будет рассмотрен далее.

Классификация кабелей согласно международному стандарту

Витые пары проводов используются в дешёвых и наиболее популярных кабелях. Кабель на основе витых пар представляет собой несколько пар скрученных попарно изолированных медных проводов в единой диэлектрической (пластиковой) оболочке. Он довольно гибкий и удобный для прокладки. Скручивание проводов позволяет свести к минимуму индуктивные наводки кабелей друг на друга и снизить влияние переходных процессов.

Согласно стандарту EIA/TIA 568, различают пять основных и две дополнительные категории кабелей на основе неэкранированной витой пары (UTP):

Кабель категории 1 — это обычный телефонный кабель (пары проводов не витые), по которому можно передавать только речь. Этот тип кабеля имеет большой разброс параметров (волнового сопротивления, полосы пропускания, перекрёстных наводок).

Кабель категории 2 — это кабель из витых пар для передачи данных в полосе частот до 1 МГц. Кабель не тестируется на уровень перекрёстных наводок. В настоящее время он используется очень редко. Стандарт EIA/TIA 568 не различает кабели категорий 1 и 2.

Кабель категории 3 — это кабель для передачи данных в полосе частот до 16 МГц, состоящий из витых пар с девятью витками проводов на метр длины. Кабель тестируется на все параметры и имеет волновое сопротивление 100 Ом. Это самый простой тип кабелей, рекомендованный стандартом для локальных сетей, однако сейчас повсеместно вытесняется кабелем категории 5.

Кабель категории 4 — это кабель, передающий данные в полосе частот до 20 МГц. Используется редко, так как не слишком заметно отличается от категории 3. Стандартом рекомендуется вместо кабеля категории 3 переходить сразу на кабель категории 5. Кабель категории 4 тестируется на все параметры и имеет волновое сопротивление 100 Ом. Кабель был создан для работы в сетях по стандарту IEEE 802.5.

Кабель категории 5 — в настоящее время самый совершенный кабель, рассчитанный на передачу данных в полосе частот до 100 МГц. Состоит из витых пар, имеющих не менее 27 витков на метр длины (8 витков на фут). Кабель тестируется на все параметры и имеет волновое сопротивление 100 Ом. Рекомендуется применять его в современных высокоскоростных сетях типа Fast Ethernet и TPFDDI. Кабель категории 5 примерно на 30—50 % дороже, чем кабель категории 3.

Кабель категории. 6 — перспективный тип кабеля для передачи данных в полосе частот до 200 (или 250) МГц.

Кабель категории 7 — перспективный тип кабеля для передачи данных в полосе частот до 600 МГц.

Согласно стандарту EIA/TIA 568, полное волновое сопротивление наиболее совершенных кабелей категорий 3, 4 и 5 должно составлять 100 Ом ±15% в частотном диапазоне от 1 МГц до максимальной частоты кабеля.

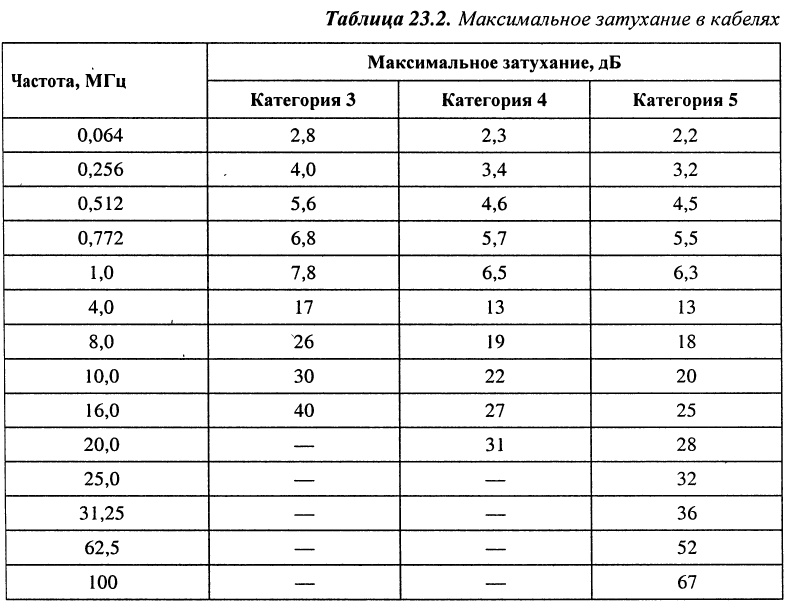
Второй важнейший параметр, задаваемый стандартом, — это максимальное затухание сигнала, передаваемого по кабелю, на разных частотах. В табл. 23.2 приведены предельные значения величины затухания в децибелах для кабелей категорий 3, 4 и 5 на расстояние 305 м (то есть 1000 футов) при нормальной температуре окружающей среды 20 °С.

Из таблицы видно, что величины затухания на частотах, близких к предельным, для всех кабелей весьма значительны. Даже на небольших расстояниях сигнал ослабляется в десятки и сотни раз, что предъявляет высокие требования к приёмникам сигнала.

Ещё один важный параметр любого кабеля, не определяемый стандартом, но существенно влияющий на работоспособность сети, — это скорость распространения сигнала в кабеле или, другими словами, задержка распространения сигнала в кабеле в расчёте на единицу длины.

Производители кабелей обычно указывают величину или задержки на метр длины, или скорость распространения сигнала относительно скорости света (или NVP — Nominal Velocity of Propagation, как её часто называют в документации). Эти величины связаны формулой

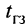
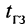
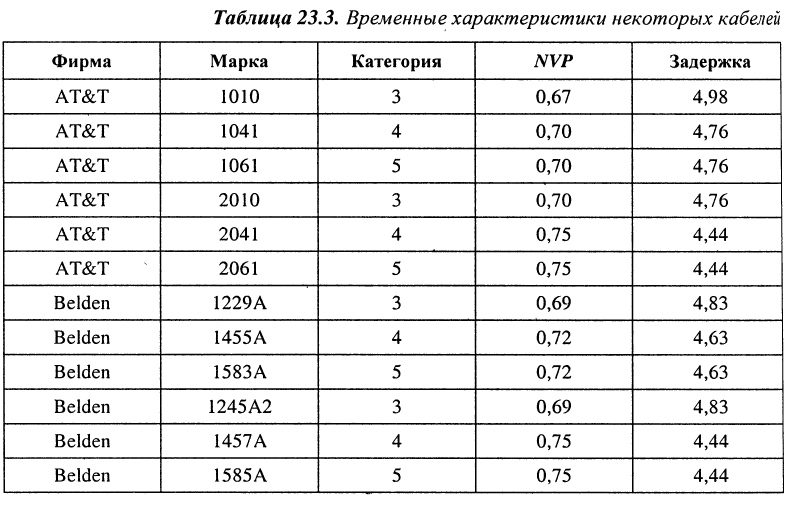
где — величина задержки на метр длины кабеля в наносекундах. Например, если NVP = 0,65 (65 % от скорости света), то задержка будет равна 5,13 нс/м. Типичная величина задержки большинства современных кабелей составляет около 4—5 нс/м.

В табл. 23.3 приведены величины NVP и задержек на метр длины (в наносекундах) для некоторых типов кабеля двух самых известных компаний-производителей AT&T и Belden.

Волновое сопротивление кабеля указывается в сопроводительной документации. Чаще всего в локальных сетях применяются 50-омные (RG-58, /?G-11, RG-8) и 93-омные кабели (RG-62). Распространённые в телевизионной технике 75-омные кабели в локальных сетях не используются. Марок коаксиального кабеля немного. Он не считается особо перспективным, поэтому в сети Fast Ethernet не предусмотрено применение коаксиальных кабелей. Однако во многих случаях классическая шинная топология (а не пассивная звезда) очень удобна, поскольку она не требует применения дополнительных устройств — концентраторов.

Типичные величины задержки распространения сигнала в коаксиальном кабеле составляют для тонкого кабеля около 5 нс/м, а для толстого — около 4,5 нс/м.

Оптоволоконный (или волоконно-оптический) кабель — это принципиально иной тип кабеля по сравнению с рассмотренными типами кабеля. Информация по нему передаётся не электрическим сигналом, а световым. Главный его элемент — это прозрачное стекловолокно, по которому свет проходит на огромные расстояния (до десятков километров) с незначительным ослаблением.

Типичная величина затухания сигнала в оптоволоконных кабелях на частотах, используемых в локальных сетях, составляет от 5 до 20 дБ/км, что примерно соответствует показателям электрических кабелей на низких частотах. Но в случае оптоволоконного кабеля при росте частоты передаваемого сигнала затухание увеличивается очень незначительно, и на больших частотах (особенно свыше 200 МГц) его преимущества перед электрическим кабелем неоспоримы: здесь он вне конкуренции.

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник