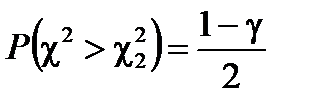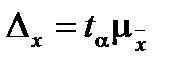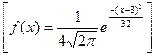построение доверительных интервалов для параметров нормального распределения

Построение доверительных интервалов для параметров нормального распределения

Интервальной оценкой математического ожидания μ нормального распределения при известной дисперсии называется интервал

, ,

удовлетворяющий равенству: , где: γ ─ заданная доверительная вероятность, μ ─ истинное математическое ожидание, ─ точечная оценка математического ожидания, n ─ объём выборки; число находится из уравнения , где ─ функция Лапласа.

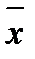
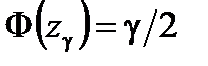
Интервальная оценка математического ожидания находится по формуле:

.

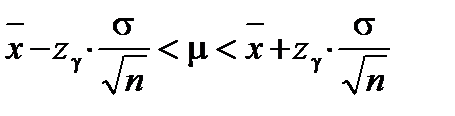
В MS Excel для вычисления величины предназначена функция (категория Статистические):

где: Альфа ─ уровень значимости , используемый для вычисления уровня надёжности . Уровень надёжности равняется процентам; Станд_откл ─ стандартное отклонение генеральной совокупности, предполагается известным; Размер ─ объём выборки n.

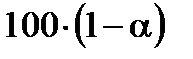
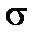
Пример 7 . По выборке объёма n=50 найдено значение выборочного среднего =3,5. Стандартное отклонение равно =2,5. Построить доверительный интервал для генерального среднего с уровнем надёжности 95%.

1. Вычислить уровень значимости: .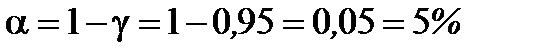

2. Ввести в ячейку А1 формулу =ДОВЕРИТ(0,05;2,5;50). В А1 появится результат: 0,693.

3. Вычислить границы доверительного интервала:

;

.

С вероятностью 0,95 математическое ожидание (генеральное среднее) принадлежит интервалу (2,807; 4,193). Математически этот вывод выражается формулой .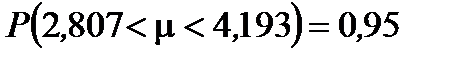

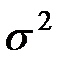
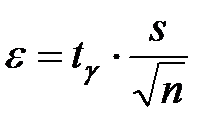
Интервальной оценкой математического ожидания μ нормального распределения при неизвестной дисперсии называется интервал:

, ,

удовлетворяющий равенству: ,

где γ ─ заданная доверительная вероятность, μ ─ истинное математическое ожидание, ─ точечная оценка математического ожидания, ─ исправленная выборочная дисперсия; n ─ объём выборки; число находится из уравнения , где ─ функция распределения Стъюдента.

Интервальная оценка математического ожидания находится по формуле:

.

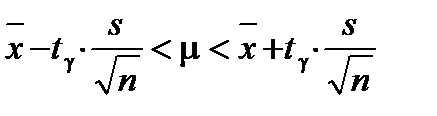
В MS Excel для вычисления величины предназначена функция (категория Статистические):

где: вероятность ─ уровень значимости ; степени_свободы ─ число степеней свободы .

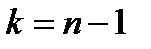
Пример 8. По выборке объёма n = 20 найдено выборочное среднее =3,5 и исправленное среднеквадратическое отклонение . Построить доверительный интервал для генерального среднего с уровнем надёжности 95%.

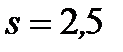
1. Ввести в ячейку А1 формулу =СТЪЮДРАСПОБР(0,05;19). В А1 появится результат: 2,093.

2. Вычислить границы доверительного интервала:

;

;

.

Доверительный интервал для генерального среднего имеет вид:

.

Доверительный интервал для генеральной дисперсии нормально распределённого признака Х определяется на основе соотношения

,

где: γ ─ заданная доверительная вероятность, ─ исправленная выборочная дисперсия; n ─ объём выборки; и определяются из условий

,

Для вычисления 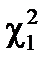и используется функция

ХИ2ОБР(вероятность; степени свободы),

Вероятность ─ значение правой части условий; степени_свободы ─ число степеней свободы .

Пример 9. Количественный признак Х генеральной совокупности распределён нормально. По выборке объёма n = 25 найдено исправленное среднеквадратическое отклонение . Найти доверительный интервал, покрывающий генеральное среднеквадратическое отклонение с надёжностью .

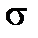
Решение в MS Excel.

, , .

2. Ввести в ячейки А1 и А2 соответственно формулы =ХИ2ОБР(0,975;24), = ХИ2ОБР(0,025;24). В ячейках появятся результаты: 12,40 и 39,36, то есть и .

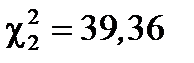
3. Найти границы интервала

; .

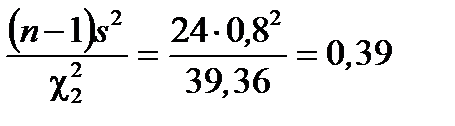
Доверительный интервал с уровнем надёжности 0,95 для генеральной дисперсии имеет вид 0,39

‒ моду (Mo) – значение изучаемого признака, повторяющегося с наибольшей частотой;

‒ исправленную выборочную дисперсию

‒ Исправленное среднее квадратическое отклонение

‒ минимальное значение выборки

‒ максимальное значение выборки

‒ сумму всех значений выборки

‒ наибольшее значение признака, имеющее разность с порядком единиц

‒ наименьшее значение признака, имеющее разность с порядком единиц

‒ уровень надёжности (предельную ошибку выборки)

Уровень надёжности. Флажок устанавливается в том случай, когда необходимо вычислить доверительный интервал для математического ожидания, соответствующий заданной доверительной вероятности (указывается в поле справа в процентах). В таблице результатов появится число, равное половине длины доверительного интервала.

К-наименьший и К-наибольший. Если флажки установлены, то появляются элементы упорядоченной выборки, расположенные на K-ом месте от её начала и от конца.

Пример 10. По полученной на занятии 1 выборке (пример 3) найти оценки числовых характеристик выборки.

Доверительный интервал для математического ожидания нормальной случайной величины при неизвестном среднем квадратическом отклонении имеет вид:

,

=СТЪЮДРАСПОБР(0,05; 29). Получим результат: 2,045. Найдём границы доверительного интервала:

(Такое же значение получается в инструменте «Описательная статистика» при вычислении параметра Уровень надёжности).

;

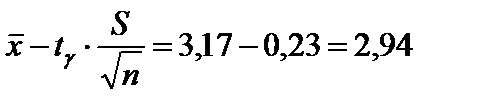
Таким образом, доверительный интервал имеет вид:

.

Задания для самостоятельной работы

Сгенерировать совокупность нормально распределённых случайных величин объёмом N для одной переменной с параметрами µ и s. Из полученной совокупности получить выборку объема n. По выборке построить гистограмму частот (число интервалов k), найти оценки числовых характеристик с использованием инструмента «Описательная статистика», построить доверительный интервал для математического ожидания.

Источник

Доверительные интервалы

Определение

Доверительные интервалы (англ. Confidence Intervals) одним из типов интервальных оценок используемых в статистике, которые рассчитываются для заданного уровня значимости. Они позволяют сделать утверждение, что истинное значение неизвестного статистического параметра генеральной совокупности находится в полученном диапазоне значений с вероятностью, которая задана выбранным уровнем статистической значимости.

Нормальное распределение

Когда известна вариация (σ 2 ) генеральной совокупности данных, для расчета доверительных пределов (граничных точек доверительного интервала) может быть использована z-оценка. По сравнению с применением t-распределения, использование z-оценки позволит построить не только более узкий доверительный интервал, но и получить более надежные оценки математического ожидания и среднеквадратического (стандартного) отклонения (σ), поскольку Z-оценка основывается на нормальном распределении.

Формула

Для определения граничных точек доверительного интервала, при условии что известно среднеквадратическое отклонение генеральной совокупности данных, используется следующая формула

где X – математическое ожидание выборки, α – уровень статистической значимости, Z_α/2 – Z-оценка для уровня статистической значимости α/2, σ – среднеквадратическое отклонение генеральной совокупности, n – количество наблюдений в выборке. При этом, σ/√ n является стандартной ошибкой.

Таким образом, доверительный интервал для уровня статистической значимости α можно записать в виде

Пример

Предположим, что размер выборки насчитывает 25 наблюдений, математическое ожидание выборки равняется 15, а среднеквадратическое отклонение генеральной совокупности составляет 8. Для уровня значимости α=5% Z-оценка равна Z_α/2=1,96. В этом случае нижняя и верхняя граница доверительного интервала составят

А сам доверительный интервал может быть записан в виде

Таким образом, мы можем утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности попадет в диапазон от 11,864 до 18,136.

Методы сужения доверительного интервала

Допустим, что диапазон [11,864; 18,136] является слишком широким для целей нашего исследования. Уменьшить диапазон доверительного интервала можно двумя способами.

Снизив уровень статистической значимости до α=10%, мы получим Z-оценку равную Z_α/2=1,64. В этом случае нижняя и верхняя граница интервала составят

А сам доверительный интервал может быть записан в виде

В этом случае, мы можем сделать предположение, что с вероятностью 90% математическое ожидание генеральной совокупности попадет в диапазон [12,376; 17,624].

Если мы хотим не снижать уровень статистической значимости α, то единственной альтернативой остается увеличение объема выборки. Увеличив ее до 144 наблюдений, получим следующие значения доверительных пределов

Сам доверительный интервал станет иметь следующий вид

Таким образом, сужение доверительного интервала без снижения уровня статистической значимости возможно только лишь за счет увеличения объема выборки. Если увеличение объема выборки не представляется возможным, то сужение доверительного интервала может достигаться исключительно за счет снижения уровня статистической значимости.

Построение доверительного интервала при распределении отличном от нормального

В случае если среднеквадратичное отклонение генеральной совокупности не известно или распределение отлично от нормального, для построения доверительного интервала используется t-распределение. Это методика является более консервативной, что выражается в более широких доверительных интервалах, по сравнению с методикой, базирующейся на Z-оценке.

Формула

Для расчета нижнего и верхнего предела доверительного интервала на основании t-распределения применяются следующие формулы

где X – математическое ожидание выборки, α – уровень статистической значимости, t_α – t-критерий Стьюдента для уровня статистической значимости α и количества степеней свободы (n-1), σ – среднеквадратическое отклонение выборки, n – количество наблюдений в выборке.

Сам доверительный интервал может быть записан в следующем виде

Распределение Стьюдента или t-распределение зависит только от одного параметра – количества степеней свободы, которое равно количеству индивидуальных значений признака (количество наблюдений в выборке). Значение t-критерия Стьюдента для заданного количества степеней свободы (n) и уровня статистической значимости α можно узнать из справочных таблиц.

Пример

Предположим, что размер выборки составляет 25 индивидуальных значений, математическое ожидание выборки равно 50, а среднеквадратическое отклонение выборки равно 28. Необходимо построить доверительный интервал для уровня статистической значимости α=5%.

В нашем случае количество степеней свободы равно 24 (25-1), следовательно соответствующее табличное значение t-критерия Стьюдента для уровня статистической значимости α=5% составляет 2,064. Следовательно, нижняя и верхняя граница доверительного интервала составят

А сам интервал может быть записан в виде

Таким образом, мы можем утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности окажется в диапазоне [38,442; 61,558].

Использование t-распределения позволяет сузить доверительный интервал либо за счет снижения статистической значимости, либо за счет увеличения размера выборки.

Снизив статистическую значимость с 95% до 90% в условиях нашего примера мы получим соответствующее табличное значение t-критерия Стьюдента 1,711.

В этом случае мы можем утверждать, что с вероятностью 90% математическое ожидание генеральной совокупности окажется в диапазоне [40,418; 59,582].

Если мы не хотим снижать статистическую значимость, то единственной альтернативой будет увеличение объема выборки. Допустим, что он составляет 64 индивидуальных наблюдения, а не 25 как в первоначальном условии примера. Табличное значение t-критерия Стьюдента для 63 степеней свободы (64-1) и уровня статистической значимости α=5% составляет 1,998.

Это дает нам возможность утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности окажется в диапазоне [43,007; 56,993].

Выборки большого объема

К выборкам большого объема относятся выборки из генеральной совокупности данных, количество индивидуальных наблюдений в которых превышает 100. Статистические исследования показали, что выборки большего объема имеют тенденцию быть нормально распределенными, даже если распределение генеральной совокупности отличается от нормального. Кроме того, для таких выборок применение z-оценки и t-распределения дают примерно одинаковые результаты при построении доверительных интервалов. Таким образом, для выборок большого объема допускается применение z-оценки для нормального распределения вместо t-распределения.

Подведем итоги

В таблице собраны рекомендации по выбору методики построения доверительных интервалов для различных ситуаций.

Источник

Доверительные интервалы для параметров нормального распределения

1. Надежность. Доверительные интервалы. Пусть — оцениваемый параметр,

— его оценка, составленная из . Если известно, что оценка является несмещенной и состоятельной, то по данным выборки вычисляют значение и считают его приближением истинного значения . При этом среднее квадратичное отклонение (если его вообще вычисляют) оценивает порядок ошибки. Такие оценки называются точечными.

Например, в предыдущем параграфе речь шла о точечных оценках генеральной средней и генеральной дисперсии. В общем случае, когда о распределении признака X ничего неизвестно, это уже немало. Если же о распределении имеется какая-либо информация, то можно сделать больше.

Здесь речь будет идти об оценке параметров а к о случайной величины,

имеющей нормальное распределение. Это очень важный случай. Например (см. § 2.7), результат измерения имеет нормальное распределение. В этом случае становится возможным применять так называемое интервальное оценивание, к изложению которого мы и переходим.

Пусть >0 некоторое число если неравенство выполняется 0 называется вероятность у того, что интервал ( — , + ) покроет параметр т.е.

где коэффициент В_n зависит от объема выборки.

* Стьюдент — псевдоним английского статистика И. О. Госсета.

Потребуем, чтобы выполнялось соотношение

Р(|Т| 30 распределение Стьюдента практически не отличается от нормированного нормального распределения(см. § 2.7, п. 2).

4. Доверительный интервал для среднего квадратичного отклонения. Для нахождения доверительного интервала для среднего квадратичного отклонения а будем использовать следующее предложение, устанавливаемое аналогично двум предыдущим

С надежностью γ можно утверждать, что доверительный интервал (s-sq; s+sq) покрывает неизвестный параметр σ; точность оценки δ = sq.

В приложении 5 приведена таблица значений q=q(γ, n) для различных значений n и обычно задаваемых значений надежности γ.

Пример 1. Признак X распределен в генеральной совокупности нормально. Найдем доверительный интервал для ог с надежностью γ =0,95, если n = 20; s=0,40. Для надежности

γ =0,95 и n = 20 находим в таблице приложения 5 q = 0,37. Далее, sq = 0,40*0,37 = 0,15.

Границы доверительного интервала 0,40-0,15= 0,25 и 0,40 + 0,15 = 0,55. Итак, доверительный интервал (0,25; 0,55) покрывает σ_r с надежностью 0,95.

Пример 2. На ферме испытывалось влияние витаминов на прибавку в массе телят. С этой целью было осмотрено 20 телят одного возраста. Средняя масса их оказалась равной 340 кг, а «исправленное» среднее квадратичное отклонение — 20 кг.

1) доверительный интервал для математического ожидания а с

надежностью 0,95; 2) доверительный интервал для среднего квадратичного отклонения с той же надежностью.

При решении задачи будем исходить из предположения, что данные пробы взяты из нормальной генеральной совокупности.

Можно считать, что в данном случае истинная масса измерена достаточно точно (отклонение порядка 9,4/340= 0,03).

подтверждается опытом). Таким образом, все предположения, которые были сделаны при выводе доверительных интервалов в пп. 2 и 3 настоящего параграфа, выполняются,

следовательно, мы вправе использовать полученные в них предложения. Так как обычно а неизвестно, следует пользоваться предложением, найденным в п. 3 данного параграфа.

Пример. По данным девяти независимых равноточных измерений физической величины найдены среднее арифметическое результатов отдельных измерений х_B = 42,319 и «исправленное» среднее квадратичное отклонение s = 5,0.

Требуется оценить истинное значение а измеряемой величины с надежностью γ =0,99.

Истинное значение измеряемой величины равно ее математическому ожиданию. Поэтому задача сводится к оценке математического ожидания (при неизвестном σ) при помощи доверительного интервала

покрывающего а с заданной надежностью γ =0,99.

Пользуясь таблицей приложения 4 по γ =0,99 и n = 9, находим t_γ=3,36.

Найдем точность оценки:

δ = t_γs/√n = 3,36*5/√9 = 3,36*5/3 = 5,60.

Границы доверительного интервала

и 42,319 + 5,60 = 47,919.

Итак, с надежностью γ =0,99 истинное значение измеренной величины а заключено в доверительном интервале 36,719 1/3

Найдите вероятность того, что в результате испытания величина X примет значение, заключенное в интервале (0; 1/3)

18. Случайная величина X на всей оси Ох задана интегральной функ­цией F(x)= . Найдите вероятность того, что в результате ис­пытания величина X примет значение, заключенное в интервале (0; 1).

19. Случайная величина X задана интегральной функцией

20. Функция

является плотностью вероятности случайной величины X. Найдите коэф­фициент а и функцию распределения F(x).

[ ]

21. Случайная величина Х задана по всей оси Ох плотностью вероятности

Найдите постоянный параметр а.

22. Случайная величина X задана плотностью вероятности

0 при х

Найдите коэффициент а. [a=1 ]

23. Случайная величина X задана плотностью вероятности f(x) = 2/3sin3x в интервале (0;П/3), вне этого интервала f(х) = 0. Найдите вероятность того, что X примет значение, принадлежащее интервалу (П/6;П/4)

[ ]

24. Случайная величина X задана плотностью вероятности

Найдите математическое ожидание случайной величины X

25. Случайная величина X задана плотностью вероятности

Найдите математическое ожидание и дисперсию случайной величины X.

26. Два равносильных шахматиста играют в шахматы. Что вероятнее выиграть: одну партию из двух или две партии из четырех (ничьи во внимание не принимаются)?

[Вероятнее выиграть одну партию из двух]

27. Пусть всхожесть семян данного растения составляет 70%. Опре­делите вероятность того, что из трех посеянных семян взойдут: а) два; б) не менее двух.- [а) 0,441; б) 0,784]

28. В семье пятеро детей. Найдите вероятность того, что среди этих детей два мальчика. Вероятность рождения мальчика принять равной 0,51.

29. Монету бросали четыре раза. Чему равна при этом вероятность вы­падения герба два раза?

30. Монета подбрасывается три раза. Какова вероятность того, что герб появится не менее двух раз?

31. Монета подбрасывается три раза. Рассматривается случайная вели­чина X— число появлений герба. Найдите закон распределения случайной величины X.

32. Найдите математическое ожидание числа бракованных изделий в партии из 10 000 изделий, если каждое изделие может оказаться брако­ванным с вероятностью 0,005.

33. Из всей выпускаемой фабрикой продукции 98% составляют изде­лия со Знаком качества. Найдите: а) математическое ожидание и б) дис­персию числа изделий со Знаком качества в партии из 5000 изделий.

34. Подлежат исследованию 1200 проб руды. Пусть вероятность про­мышленного содержания металла в каждой пробе равна 0,09. Найдите: а) математическое ожидание и б) дисперсию числа проб с промышленным содержанием металла.

35. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины X соответственно равны 3 и 2. Найдите плотность вероятности случайной величины X f(x).

36. Напишите дифференциальную функцию нормально распределен­ной случайной величины X, зная, что М(Х) = 3, D(X) = 16.

37. Нормально распределенная случайная величина X задана дифференциальной функцией

Найдите математическое ожидание и дисперсию X.

38. Математическое ожидание и среднее квадратическое отклонение нор­мально распределенной случайной величины X соответственно равны 10 и 2. Найдите вероятность того, что в результате испытания Х примет значе­ние, заключенное в интервале (12; 14).

39. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 20 и 5. Найдите вероятность того, что в результате испытания X примет значе­ние в интервале (15; 25).

40. Детали, выпускаемые цехом, по размеру диаметра распределяются по нормальному закону с параметрами: математическое ожидание равно 5 см, а среднее квадратическое отклонение равно 0,9 см. Найдите вероятность того, что отклонение диаметра наудачу взятой детали от математи­ческого ожидания по абсолютной величине будет меньше 2 см.

41. Проводится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со средним квадратическим отклонением = 20 г. Найдите вероятность того, что взвешивание будет проведено с ошибкой, которая по абсолютной ве­личине меньше 10 г.

42. АТС получает в среднем за час 300 вызовов. Какова вероятность того, что за данную минуту она получит точно 2 вызова?

43. Среди 1000 человек приблизительно 8 левшей. Какова вероятность того, что среди сотни наугад выбранных человек не окажется ни одного левши?

44. Монету подбрасывают 100 раз. Какова вероятность того, что при этом герб выпадет ровно 50 раз?

45. Какова вероятность того, что при 200-кратном бросании монеты число случаев выпадения герба удовлетворяет неравенству 95

Источник