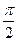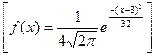построить доверительные интервалы для параметров нормального распределения

Доверительные интервалы для параметров нормального распределения

1. Надежность. Доверительные интервалы. Пусть — оцениваемый параметр,

— его оценка, составленная из . Если известно, что оценка является несмещенной и состоятельной, то по данным выборки вычисляют значение и считают его приближением истинного значения . При этом среднее квадратичное отклонение (если его вообще вычисляют) оценивает порядок ошибки. Такие оценки называются точечными.

Например, в предыдущем параграфе речь шла о точечных оценках генеральной средней и генеральной дисперсии. В общем случае, когда о распределении признака X ничего неизвестно, это уже немало. Если же о распределении имеется какая-либо информация, то можно сделать больше.

Здесь речь будет идти об оценке параметров а к о случайной величины,

имеющей нормальное распределение. Это очень важный случай. Например (см. § 2.7), результат измерения имеет нормальное распределение. В этом случае становится возможным применять так называемое интервальное оценивание, к изложению которого мы и переходим.

Пусть >0 некоторое число если неравенство выполняется 0 называется вероятность у того, что интервал ( — , + ) покроет параметр т.е.

где коэффициент В_n зависит от объема выборки.

* Стьюдент — псевдоним английского статистика И. О. Госсета.

Потребуем, чтобы выполнялось соотношение

Р(|Т| 30 распределение Стьюдента практически не отличается от нормированного нормального распределения(см. § 2.7, п. 2).

4. Доверительный интервал для среднего квадратичного отклонения. Для нахождения доверительного интервала для среднего квадратичного отклонения а будем использовать следующее предложение, устанавливаемое аналогично двум предыдущим

С надежностью γ можно утверждать, что доверительный интервал (s-sq; s+sq) покрывает неизвестный параметр σ; точность оценки δ = sq.

В приложении 5 приведена таблица значений q=q(γ, n) для различных значений n и обычно задаваемых значений надежности γ.

Пример 1. Признак X распределен в генеральной совокупности нормально. Найдем доверительный интервал для ог с надежностью γ =0,95, если n = 20; s=0,40. Для надежности

γ =0,95 и n = 20 находим в таблице приложения 5 q = 0,37. Далее, sq = 0,40*0,37 = 0,15.

Границы доверительного интервала 0,40-0,15= 0,25 и 0,40 + 0,15 = 0,55. Итак, доверительный интервал (0,25; 0,55) покрывает σ_r с надежностью 0,95.

Пример 2. На ферме испытывалось влияние витаминов на прибавку в массе телят. С этой целью было осмотрено 20 телят одного возраста. Средняя масса их оказалась равной 340 кг, а «исправленное» среднее квадратичное отклонение — 20 кг.

1) доверительный интервал для математического ожидания а с

надежностью 0,95; 2) доверительный интервал для среднего квадратичного отклонения с той же надежностью.

При решении задачи будем исходить из предположения, что данные пробы взяты из нормальной генеральной совокупности.

Можно считать, что в данном случае истинная масса измерена достаточно точно (отклонение порядка 9,4/340= 0,03).

подтверждается опытом). Таким образом, все предположения, которые были сделаны при выводе доверительных интервалов в пп. 2 и 3 настоящего параграфа, выполняются,

следовательно, мы вправе использовать полученные в них предложения. Так как обычно а неизвестно, следует пользоваться предложением, найденным в п. 3 данного параграфа.

Пример. По данным девяти независимых равноточных измерений физической величины найдены среднее арифметическое результатов отдельных измерений х_B = 42,319 и «исправленное» среднее квадратичное отклонение s = 5,0.

Требуется оценить истинное значение а измеряемой величины с надежностью γ =0,99.

Истинное значение измеряемой величины равно ее математическому ожиданию. Поэтому задача сводится к оценке математического ожидания (при неизвестном σ) при помощи доверительного интервала

покрывающего а с заданной надежностью γ =0,99.

Пользуясь таблицей приложения 4 по γ =0,99 и n = 9, находим t_γ=3,36.

Найдем точность оценки:

δ = t_γs/√n = 3,36*5/√9 = 3,36*5/3 = 5,60.

Границы доверительного интервала

и 42,319 + 5,60 = 47,919.

Итак, с надежностью γ =0,99 истинное значение измеренной величины а заключено в доверительном интервале 36,719 1/3

Найдите вероятность того, что в результате испытания величина X примет значение, заключенное в интервале (0; 1/3)

18. Случайная величина X на всей оси Ох задана интегральной функ­цией F(x)= . Найдите вероятность того, что в результате ис­пытания величина X примет значение, заключенное в интервале (0; 1).

19. Случайная величина X задана интегральной функцией

20. Функция

является плотностью вероятности случайной величины X. Найдите коэф­фициент а и функцию распределения F(x).

[ ]

21. Случайная величина Х задана по всей оси Ох плотностью вероятности

Найдите постоянный параметр а.

22. Случайная величина X задана плотностью вероятности

0 при х

Найдите коэффициент а. [a=1 ]

23. Случайная величина X задана плотностью вероятности f(x) = 2/3sin3x в интервале (0;П/3), вне этого интервала f(х) = 0. Найдите вероятность того, что X примет значение, принадлежащее интервалу (П/6;П/4)

[ ]

24. Случайная величина X задана плотностью вероятности

Найдите математическое ожидание случайной величины X

25. Случайная величина X задана плотностью вероятности

Найдите математическое ожидание и дисперсию случайной величины X.

26. Два равносильных шахматиста играют в шахматы. Что вероятнее выиграть: одну партию из двух или две партии из четырех (ничьи во внимание не принимаются)?

[Вероятнее выиграть одну партию из двух]

27. Пусть всхожесть семян данного растения составляет 70%. Опре­делите вероятность того, что из трех посеянных семян взойдут: а) два; б) не менее двух.- [а) 0,441; б) 0,784]

28. В семье пятеро детей. Найдите вероятность того, что среди этих детей два мальчика. Вероятность рождения мальчика принять равной 0,51.

29. Монету бросали четыре раза. Чему равна при этом вероятность вы­падения герба два раза?

30. Монета подбрасывается три раза. Какова вероятность того, что герб появится не менее двух раз?

31. Монета подбрасывается три раза. Рассматривается случайная вели­чина X— число появлений герба. Найдите закон распределения случайной величины X.

32. Найдите математическое ожидание числа бракованных изделий в партии из 10 000 изделий, если каждое изделие может оказаться брако­ванным с вероятностью 0,005.

33. Из всей выпускаемой фабрикой продукции 98% составляют изде­лия со Знаком качества. Найдите: а) математическое ожидание и б) дис­персию числа изделий со Знаком качества в партии из 5000 изделий.

34. Подлежат исследованию 1200 проб руды. Пусть вероятность про­мышленного содержания металла в каждой пробе равна 0,09. Найдите: а) математическое ожидание и б) дисперсию числа проб с промышленным содержанием металла.

35. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины X соответственно равны 3 и 2. Найдите плотность вероятности случайной величины X f(x).

36. Напишите дифференциальную функцию нормально распределен­ной случайной величины X, зная, что М(Х) = 3, D(X) = 16.

37. Нормально распределенная случайная величина X задана дифференциальной функцией

Найдите математическое ожидание и дисперсию X.

38. Математическое ожидание и среднее квадратическое отклонение нор­мально распределенной случайной величины X соответственно равны 10 и 2. Найдите вероятность того, что в результате испытания Х примет значе­ние, заключенное в интервале (12; 14).

39. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 20 и 5. Найдите вероятность того, что в результате испытания X примет значе­ние в интервале (15; 25).

40. Детали, выпускаемые цехом, по размеру диаметра распределяются по нормальному закону с параметрами: математическое ожидание равно 5 см, а среднее квадратическое отклонение равно 0,9 см. Найдите вероятность того, что отклонение диаметра наудачу взятой детали от математи­ческого ожидания по абсолютной величине будет меньше 2 см.

41. Проводится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со средним квадратическим отклонением = 20 г. Найдите вероятность того, что взвешивание будет проведено с ошибкой, которая по абсолютной ве­личине меньше 10 г.

42. АТС получает в среднем за час 300 вызовов. Какова вероятность того, что за данную минуту она получит точно 2 вызова?

43. Среди 1000 человек приблизительно 8 левшей. Какова вероятность того, что среди сотни наугад выбранных человек не окажется ни одного левши?

44. Монету подбрасывают 100 раз. Какова вероятность того, что при этом герб выпадет ровно 50 раз?

45. Какова вероятность того, что при 200-кратном бросании монеты число случаев выпадения герба удовлетворяет неравенству 95

Источник

Доверительный интервал

Классификация доверительных интервалов

Расчет средней ошибки выборки при случайном отборе

Расхождение между значениями показателей, полученных по выборке, и соответствующими параметрами генеральной совокупности называется ошибкой репрезентативности.
Обозначения основных параметров генеральной и выборочной совокупности.

Характеристики	Генеральная совокупность	Выборочная совокупность
Объем совокупности (численность единиц)	N	n
Численность единиц, обладающих обследуемым качеством (признаком)	M	m
Доля единиц, обладающих обследуемым качеством (признаком), выборочная доля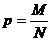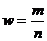

Формулы средней ошибки выборки
повторный отбор		бесповторный отбор
для средней	для доли	для средней	для доли

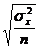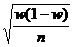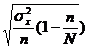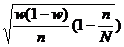Соотношение между пределом ошибки выборки (_Δ), гарантируемым с некоторой вероятностью Р(t), и средней ошибкой выборки имеет вид: 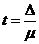или Δ = t·μ, где t– коэффициент доверия, определяемый в зависимости от уровня вероятности Р(t) по таблице интегральной функции Лапласа.

Формулы расчета численности выборки при собственно-случайном способе отбора

Способ отбора	Формулы определения численности выборки
	для средней	для доли
Повторный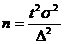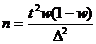
Бесповторный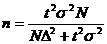

Найти численность выборки можно, использовав калькулятор.

Метод доверительных интервалов

Решение ищем по формуле определения численности выборки для повторного отбора.

Ф(t_kp) = γ/2 = 0.997/2 = 0,4985 и этому значению по таблице Лапласа соответствует t_kp =2.96.
w = 9% = 0,09
Δ = 4% = 0,04
Итого: n = 2.96 2 *0,09(1-0,09)/0,04 2 = 448,4844 ≈ 449

1. Используя результаты расчетов, выполненных в задании № 2 и полагая, что эти данные получены при помощи собственно-случайного 10-ти процентного бесповторного отбора, определить:
а) пределы, за которые с доверительной вероятностью 0,954 не выйдет среднее значение признака, рассчитанное по генеральной совокупности;
б) как нужно изменить объем выборки, чтобы снизить предельную ошибку средней величины на 50%.
2. Используя результаты расчетов, выполненных в задании № 2 и полагая, что эти данные получены при помощи повторного отбора, определить:
а) пределы, за которые в генеральной совокупности не выйдет значение доли предприятий, у которых индивидуальные значения признака превышают моду с доверительной вероятностью 0,954;
б) как изменить объем выборки, чтобы снизить предельную ошибку доли на 20 %.
Методические указания

Задание. Поточная линия по производству однотипных деталей подвергалась реконструкции Заданы две выборки отображающие процент брака в партиях деталей выпускаемых на данной линии до и после реконструкции Можно ли достоверно утверждать, что после реконструкции процент брака в партиях деталей снизился?

2. Вводим исходные данные.

Поле «Доверительный интервал генерального среднего, дисперсия и среднеквадратическое отклонения » указываем значение γ = 0.95 (что соответствует α=0.05).

В поле « Выборка » указываем значение 10 (поскольку из 49 значений выбрали 5, что соответствует 10,2% (5/49×100%)).

Решение.
Используя результаты расчетов, выполненных в задании № 2 и полагая, что эти данные получены при помощи повторного отбора, определить:
а) пределы, за которые в генеральной совокупности не выйдет значение доли предприятий, у которых индивидуальные значения признака превышают моду с доверительной вероятностью 0.954 ;
б) как изменить объем выборки, чтобы снизить предельную ошибку доли на 20%.

Задание №5: На заводе электроламп из партии продукции в количестве 16000 шт. ламп взято на выборку 1600 шт. (случайный, бесповторный отбор), из которых 40 шт. оказались бракованными. Определить с вероятностью 0.997 пределы, в которых будет находиться процент брака для всей партии продукции.

Источник

Нормальное распределение (Гаусса) в Excel

В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.

Нормальное распределение в статистике

История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.

Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.

Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.

Кривая нормального распределения Гаусса имеет следующий вид.

График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.

На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.

Формула нормального распределения (плотности) следующая.

Формула состоит из двух математических констант:

е – основание натурального логарифма 2,718;

двух изменяемых параметров, которые задают форму конкретной кривой:

m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);

ну и сама переменная x, для которой высчитывается плотность вероятности.

Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии ( σ 2 ). Кратко обозначается N(m, σ 2 ) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ 2 характеризует размах вариации, то есть «размазанность» данных.

Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.

А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.

Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.

Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:

Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как

P(a ≤ X 0 =1 и остается рассчитать только соотношение 1 на корень из 2 пи.

Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.

Функция стандартного нормального распределения позволяет рассчитывать вероятности.

Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.

Таблица нормального распределения

Таблицы нормального распределения встречаются двух типов:

— таблица плотности;

— таблица функции (интеграла от плотности).

Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.

В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец 0, т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).

Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.

Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.

На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.

В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.

Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:

Это факт показан на картинке:

Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.

Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:

Для наглядности можно взглянуть на рисунок.

На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.

Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:

Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.

Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.

Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:

Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.

Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.

Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.

То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.

Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).

Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).

Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.

Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.

Так выглядит правило 3 сигм для нормального распределения на диаграмме.

С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.

Нормальное распределение в Excel

В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.

Функция НОРМ.СТ.РАСП

Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ( z ) или вероятности Φ(z) по нормированным данным (z).

z – значение стандартизованной переменной

интегральная – если 0, то рассчитывается плотность ϕ( z ) , если 1 – значение функции Ф(z), т.е. вероятность P(Z