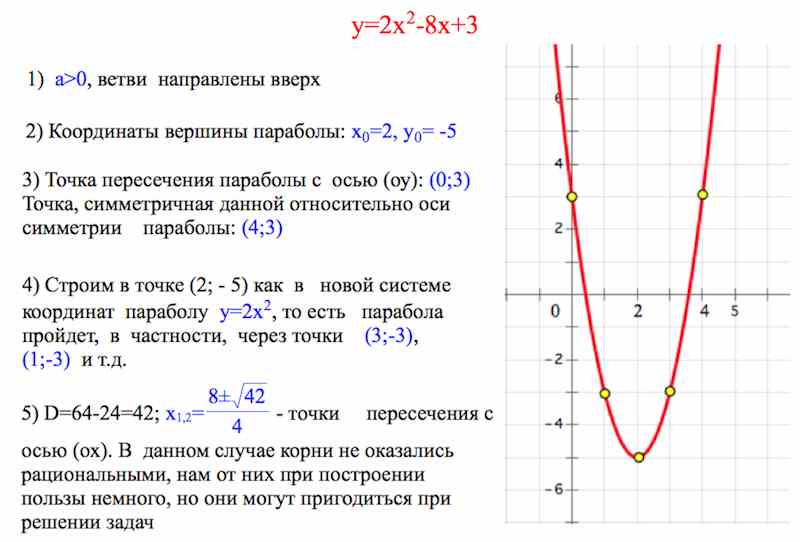
построить параболу по параметру
Квадратичная функция. Построение Параболы
8 класс, 9 класс, ЕГЭ/ОГЭ
Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Построение квадратичной функции
Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:
График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.
График функции y = –x 2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
Рассмотрим три случая:
Если a > 0, то график выглядит как-то так:
0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>
На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.
Как строим:
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
Как строим:
Уравнение квадратичной функции имеет вид y = (x + a) * (x + b)
Как строим:
Квадратичная функция. Парабола
Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют функцией в математике.
Если вы прочно закрепите общие знания о функции (способы задания, понятие графика) дальнейшее изучение других видов функций будет даваться значительно легче.
Что называют квадратичной функцией
Квадратичная функция — это функция вида
Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень, в которой стоит « x » — это « 2 », то перед нами квадратичная функция.
Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты « a », « b » и « с ».
Как построить график квадратичной функции
График квадратичной функции называют параболой.
Парабола выглядит следующим образом.
Также парабола может быть перевернутой.
Существует четкий алгоритм действий при построении графика квадратичной функции. Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.
Чтобы было проще понять этот алгоритм, сразу разберем его на примере.
Построим график квадратичной функции « y = x 2 −7x + 10 ».
Если « a > 0 », то ветви направлены вверх. 
Если « a », то ветви направлены вниз. 
В нашей функции « a = 1 », это означает, что ветви параболы направлены вверх.
Чтобы найти « x0 » (координата вершины по оси « Ox ») нужно использовать формулу:
Найдем « x0 » для нашей функции « y = x 2 −7x + 10 ».
Теперь нам нужно найти « y0 » (координату вершины по оси « Oy »). Для этого нужно подставить найденное значение « x0 » в исходную функцию. Вспомнить, как найти значение функции можно в уроке «Как решать задачи на функцию» в подразделе «Как получить значение функции».
Выпишем полученные координаты вершины параболы.
(·) A (3,5; −2,25) — вершина параболы.
Отметим вершину параболы на системе координат. Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график относительно оси « Oy ».
Для начала давайте разберемся, что называют нулями функции.
Нули функции — это точки пересечения графика функции с осью « Ox » (осью абсцисс).
Наглядно нули функции на графике выглядят так:
Свое название нули функции получили из-за того, что у этих точек координата по оси « Oy » равна нулю.
Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.
Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо « y = 0 ».
0 = x 2 −7x + 10
x 2 −7x + 10 = 0
x1;2 =
| 7 ± √ 49 − 4 · 1 · 10 |
| 2 · 1 |
x1;2 =
| 7 ± √ 9 |
| 2 |
x1;2 =
| 7 ± 3 |
| 2 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
| x1 = 5 | x2 = 2 |
Мы получили два корня в уравнении, значит, у нас две точки пересечения с осью « Ox ». Назовем эти точки и выпишем их координаты.
Отметим полученные точки («нули функции») на системе координат.
Возьмем четыре произвольные числовые значения для « x ». Целесообразно брать целые числовые значения на оси « Ox », которые наиболее близки к оси симметрии. Числа запишем в таблицу в порядке возрастания.
Для каждого выбранного значения « x » рассчитаем « y ».
Запишем полученные результаты в таблицу.
| x | 1 | 3 | 4 | 6 |
| y | 4 | −2 | −2 | 4 |
Отметим полученные точки графика на системе координат (зеленые точки).
Теперь мы готовы построить график. На забудьте после построения подписать график функции.
Краткий пример построения параболы
Рассмотрим другой пример построения графика квадратичной функции. Только теперь запишем алгоритм построения коротко без подробностей.
Пусть требуется построить график функции « y = −3x 2 − 6x − 4 ».
x0 =
| −b |
| 2a |
x0 =
| −(−6) |
| 2 · (−3) |
=
| 6 |
| −6 |
= −1
y0(−1) = (−3) · (−1) 2 − 6 · (−1) − 4 = −3 · 1 + 6 − 4 = −1
(·) A (−1; −1) — вершина параболы.
Точки пересечения с осью « Ox » ( y = 0 ).
x1;2 =
| −6 ± √ 6 2 − 4 · 3 · 4 |
| 2 · 1 |
x1;2 =
| −6 ± √ 36 − 48 |
| 2 |
x1;2 =
| −6 ± √ −12 |
| 2 |
Ответ: нет действительных корней.
Так как корней нет, значит, график функции не пересекает ось « Ox ».
Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые не выходят за масштаб нашей системы координат, то есть точки « (−2; −4) » и « (0; −4) ». Построим и подпишем график функции.
Построение графика квадратичной функции (ЕГЭ 2022)
Чтобы понять то, что здесь будет написано, тебе нужно хорошо знать, что такое квадратичная функция.
Проверь себя, ответь на эти вопросы:
Если ты сходу смог ответить, продолжай читать.
Если хоть один вопрос вызвал затруднения, повтори тему «Квадратичная функция».
График квадратичной функции – коротко о главном
Определение
Квадратичная функция – функция вида \( y=a<
^<2>>+bx+c\), где \( a\ne 0\), \( b\) и \( c\) – любые числа (коэффициенты), \( c\) – свободный член.
График квадратичной функции – парабола.
| Если коэффициент \( \displaystyle a 0\) – ветви параболы направлены вверх. Чем больше значение \( \displaystyle a\) (по модулю), тем у́же становится парабола (ветви становятся более крутыми). И наоборот, чем меньше \( \displaystyle a\), тем парабола шире. |
Вершина параболы
\( \displaystyle <
Подставляем \( \displaystyle <
\( \displaystyle <
Свободный член \( \displaystyle c\) – это координата пересечения параболы с осью ординат.
Квадратичная функция и её коэффициенты
Итак, ты уже умеешь обращаться с квадратичной функцией, анализировать ее график и строить график по точкам.
Ну что же, вот она: \( y=a<
Давай вкратце вспомним, что делают коэффициенты.
С чего мы всегда начинаем строить параболу? Какая у нее есть отличительная точка?
Это вершина. А как найти координаты вершины, помнишь?
Абсцисса ищется по такой формуле:
Вот так: чем больше \( \displaystyle b\), тем левее смещается вершина параболы.
Ординату вершины можно найти, подставив \( <
Подставь сам и посчитай. Что получилось?
Если сделать все правильно и максимально упростить полученное выражение, получится:
Получается, что чем \( \displaystyle b\) больше по модулю, тем выше будет вершина параболы.
Перейдем, наконец, к построению графика.
Самый простой способ – строить параболу, начиная с вершины.
Пример №1
Построить график функции \( y=\frac<1><2><
Решение:
Для начала определим коэффициенты: \( a=\frac<1><2>;\text< >b=2;\text< >c=-1\).
Теперь вычислим координаты вершины:
А теперь вспоминаем: все параболы с одинаковым старшим коэффициентом выглядят одинаково.
Остается только один вопрос. Как быстро рисовать параболу?
Как быстро рисовать график квадратичной функции – параболу?
Даже если мы рисуем параболу с вершиной в начале координат, все равно приходится строить ее по точкам, а это долго и неудобно. А ведь все параболы выглядят одинаково, может, есть способ ускорить их рисование?
Когда я учился в школе, учительница математики сказала всем вырезать из картона трафарет в форме параболы, чтобы быстро ее чертить. Но с трафаретом везде ходить не получится, да и на экзамен его взять не разрешат. Значит, не будем пользоваться посторонними предметами, а будем искать закономерность.
Рассмотрим простейшую параболу \( y=<
Закономерность здесь такая.
Если из вершины сместиться вправо (вдоль оси \( \displaystyle Ox\)) на \( \displaystyle 1\), и вверх (вдоль оси \( \displaystyle Oy\)) на \( \displaystyle 1\), то попадем в точку параболы.
Дальше: если из этой точки сместиться вправо на \( \displaystyle 1\) и вверх на \( \displaystyle 3\), снова попадем в точку параболы.
Дальше: вправо на \( \displaystyle 1\) и вверх на \( \displaystyle 5\). Дальше что?
Вправо на \( \displaystyle 1\) и вверх на \( \displaystyle 7\).
И так далее: смещаемся на \( \displaystyle 1\) вправо, и на следующее нечетное число вверх.
То же самое потом проделываем с левой веткой (ведь парабола симметрична, то есть ее ветви выглядят одинаково):
Отлично, это поможет построить из вершины любую параболу со старшим коэффициентом, равным \( \displaystyle 1\).
Пример построения параболы быстрым способом
Например, нам стало известно, что вершина параболы находится в точке \( \displaystyle \left( 1;-2 \right)\). Построй (самостоятельно, на бумаге) эту параболу.
Должно получиться так:
Теперь соединяем полученные точки:
ОК, ну что же, теперь строить только параболы с \( \displaystyle a=1\)?
Конечно, нет. Сейчас разберемся, что с ними делать, если \( \displaystyle a\ne 1\).
Три типичных случая построения параболы
Cлучай 1. \( a=-1\).
То есть функция выглядит как \( y=-<
И то же самое, только влево.
Случай 2. \( a>1\).
Что делать, если, например, \( a=2\)?
Все просто: начинаем так же: \( 1\) вправо, но когда дело доходит до «вверх», любое число увеличиваем в \( 2\) раза:
Аналогично в случае \( a
Парабола в математике: уравнение, построение, виды
Что такое парабола в математике
Формула параболы может рассказать нам о многом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Алгоритм построения параболы
Построим график функции \(f(x)=ax^2+bx+c.\)
Примеры решения задач на построение параболы
Смещение параболы
Свободный член с смещает параболу по оси y. Например, если c=2, то парабола f(x)=ax^2+bx сместится вверх на 2 единичных отрезка, а если с=-2, то график сместится вниз так же на 2 единичных отрезка.
В случае, когда к аргументу x прибавляется или вычитается какое-либо число, график смещается по оси x. Например, для построения графика функции \(y=<(x+4)>^2\) достаточно сместить график \(y=x^2 \) на 4 единичных отрезка влево, а для построения графика \(y=<(x-3)>^2\) нужно сместить график \(y=x^2\) на 3 единичных отрезка вправо.
Парабола спешит на помощь
Муниципальное казённое образовательное учреждение
«Чебаклинская средняя общеобразовательная школа»
МКОУ «Чебаклинская СОШ»
МКОУ «Чебаклинская СОШ»
Глава 1. Построение параболы
1.1 Парабола – график квадратичной функции5-8
1.2 Парабола – геометрическое место точек
1.3 Преобразования графиков функций-19
Глава 2. Решение задач
2.1 Решение задач с помощью графика квадратичной функции20-28
2.2 Рисуем графиками
Заключение30
На первый взгляд, понятие не ново,
И не всегда подумаешь о том,
Как важно будет в жизни это слово
И сколько смысла будет в слове том!
И Кушнир, Л. Финкельштейн. «Ода функции»,
Даны: точка О и окружность С, лежащая в плоскости, не проходящей через точку О. Пусть прямая линия, бесконечная в обе стороны (как и полагается в геометрии), движется так, что она все время проходит через О и через одну из точек окружности С. При этом движении прямая описывает поверхность, состоящую из двух раструбов (полостей). Это — коническая поверхность. Если ее пересекать различными плоскостями, тоже не проходящими через точку О, то в сечении получаются кривые линии, называемые коническими сечениями. Их три типа: эллипс, гипербола и парабола. Они были известны еще в Древней Греции. Их открыл некий Менехм около 360 года до нашей эры, а до нас они дошли по замечательному сочинению выдающегося математика Аполлония, написанному примерно 200 лет спустя.
Одна из этих кривых, которая особенно меня заинтересовала – это парабола.
Вы, наверно, видели, какие яркие и ровные пучки света бросают в небо мощные прожекторы. Автомобильные фары и карманный фонарик также дают ровный пучок света. Это достигается применением параболического отражателя. Форму параболы принимает струя воды, бьющая из шланга, по параболе летит мяч или камень. Все эти процессы и многие другие можно описать с помощью уравнения квадратичной функции, графиком которой является парабола.
Задачи с параметрами на квадратичную функцию и задачи, сводящиеся к квадратичным функциям, очень популярны на экзаменах в вузы, ЕГЭ, школьных олимпиадах разного уровня. Квадратичная функция является одной из главных в школьной математике, для которой построена полная теория и доказаны все свойства, а от учащегося требуется четкое понимание и знание всех этих свойств. При этом задач на квадратичную функцию очень много – от простых, непосредственно вытекающих из формул и теории, до сложных, требующих всестороннего анализа и глубокого понимания свойств функции.
Проблема нашего исследования, таким образом, состоит в следующем – выяснить, как можно с помощью параболы решать более сложные задачи.
Объект исследования – парабола
Предмет исследования – способы построения парабол и применение парабол при решении задач.
Проблема, объект и предмет исследования определили тему нашего исследования «Парабола спешит на помощь ».
Цель – изучение и систематизация всех полученных знаний о параболе и применение параболы для решения задач.
Задачи исследования:
ü Изучить разные способы построения параболы и виды преобразований графиков.
ü Рассмотреть примеры построения графиков сложных функций.
ü Решить задачи разных типов с помощью параболы.
ü Научиться строить графики с помощью программы «AGrapherSetup».
Методы исследования: анализ, синтез, обобщение
Глава 1. Построение параболы
· Рассмотреть разные способы построения параболы.
· Изучить преобразования графиков функций.
· Научиться строить графики сложных функций с помощью преобразований.
1.2 Парабола – график квадратичной функции
Графиком квадратичной функции y= ax² +bx+c является квадратичная парабола.
При построении графика необходимо обращать на старший коэффициент а.
Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.
Если старший коэффициент a ;
ü влево, если 
.
Параллельный перенос графика вдоль оси ординат на 
единиц
ü вверх, если 
0″ width=»46″ height=»14 «/>,
ü вниз, если .
Симметричное отражение графика относительно оси ординат.
Симметричное отражение графика относительно оси абсцисс.
ü При 
1″ width=»45″ height=»15″/> — сжатие графика к оси ординат в 
раз,
ü при 
— растяжение графика от оси ординат в 
раз.
ü При 1″ width=»45″ height=»15″/> — растяжение графика от оси абсцисс в раз,
ü при — cжатие графика к оси абсцисс в раз.
ü При 
— график остаётся без изменений,
ü при 
— график симметрично отражается относительно оси абсцисс.
ü При 
— график остаётся без изменений,
ü при 
— график симметрично отражается относительно оси ординат.
Материал из Википедии — свободной энциклопедии
Рассмотрим подробно, как выполняются преобразования графиков на примерах.
Параллельный перенос по оси Ох.
Параллельный перенос графика функции у = ах2 вдоль оси х на |m|
(вправо при m > 0 и влево при т 0 и вниз при п 1) получается с помощью сжатия графика функции y = f(x) вдоль оси Оx в k раз.
y(2x)=2(2x)²+4(2x)-5
Растяжение: График функции y=f(kx)
(1 >k > 0) получается с помощью растяжения графика функции y = f(x) вдоль оси Oх в 1/k раз.
y(0.3x)=2(0.3x)²+4(0.3x)-5
При этом в обоих случаях точки пересечения графика с осью Oу остаются неизменными.
График функции у = kf(x) получается из графика функции у = f(x) растяжением или сжатием вдоль оси Oy:
при k > 1 происходит растяжение графика,
2y(x)=2(2x²+4x-5)