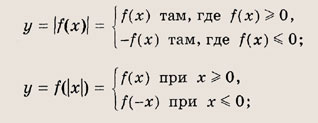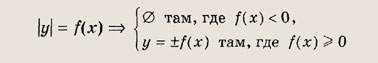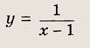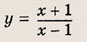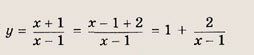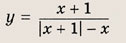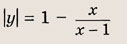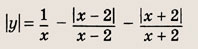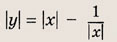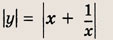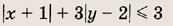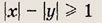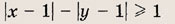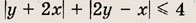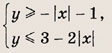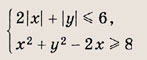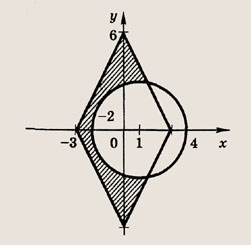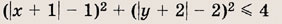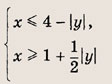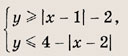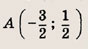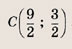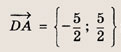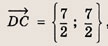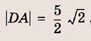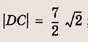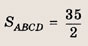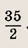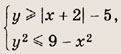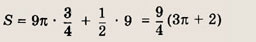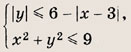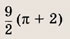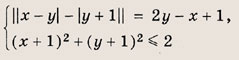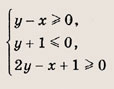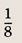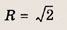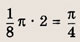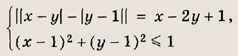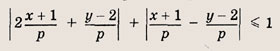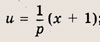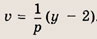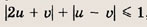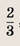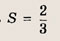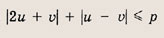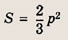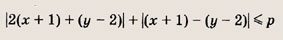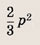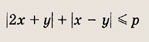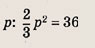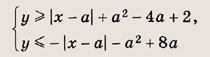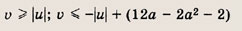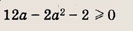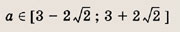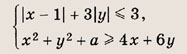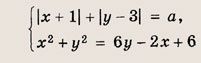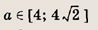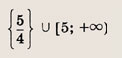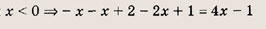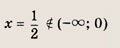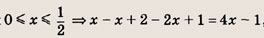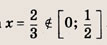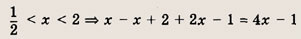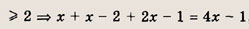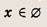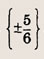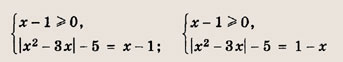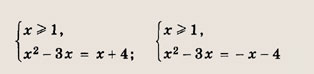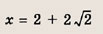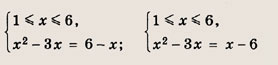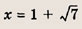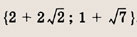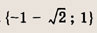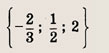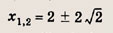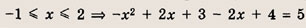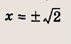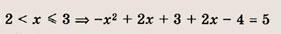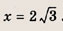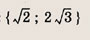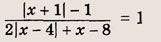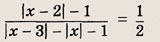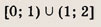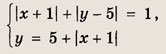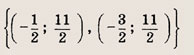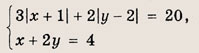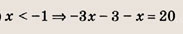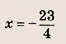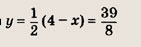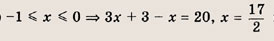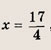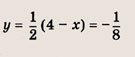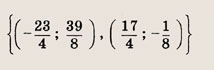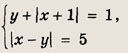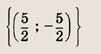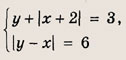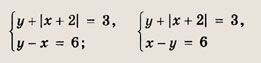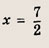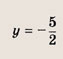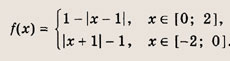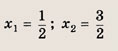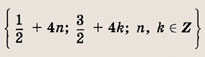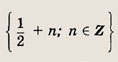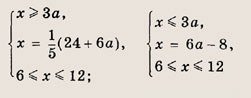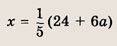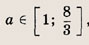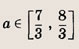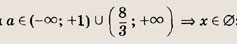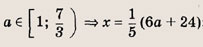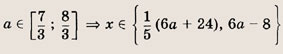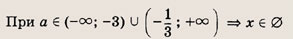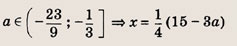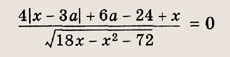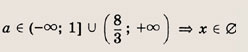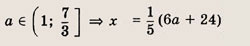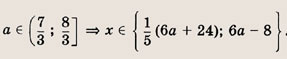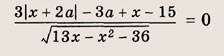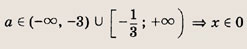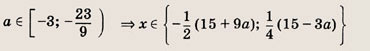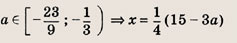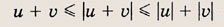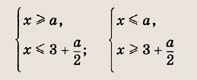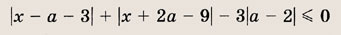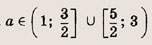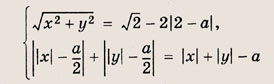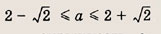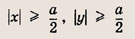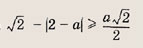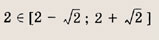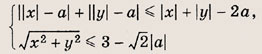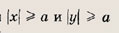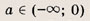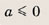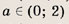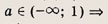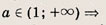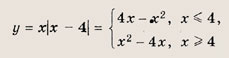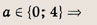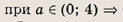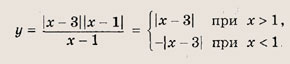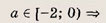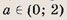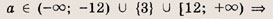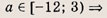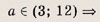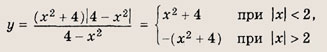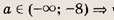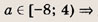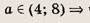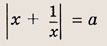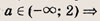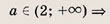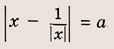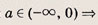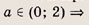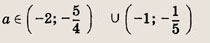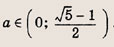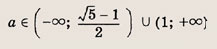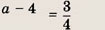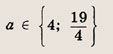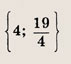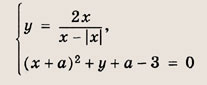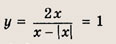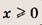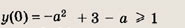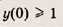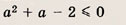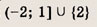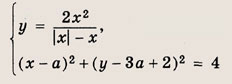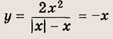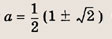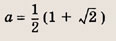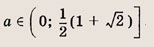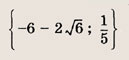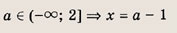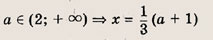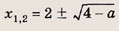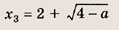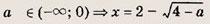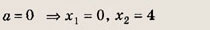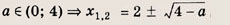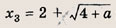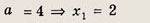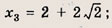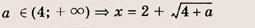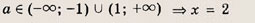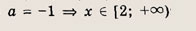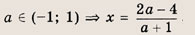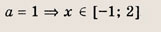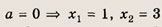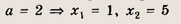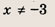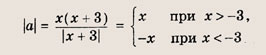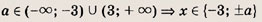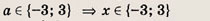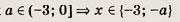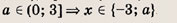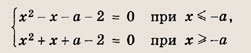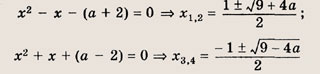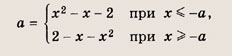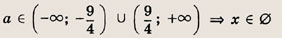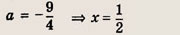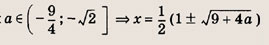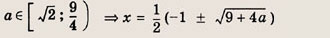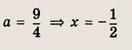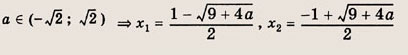при каких значениях параметра площадь фигуры заданной системой неравенств равна

При каких значениях параметра площадь фигуры заданной системой неравенств равна

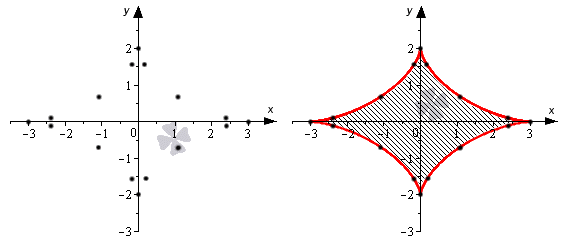
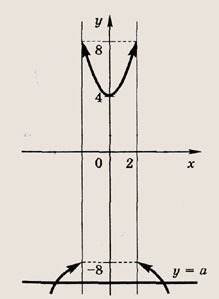
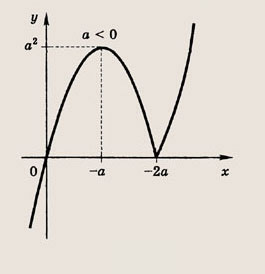
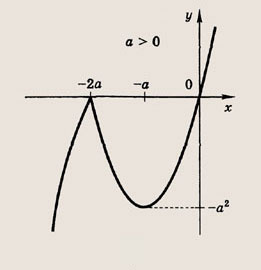
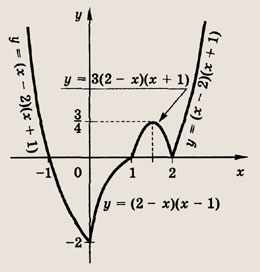
При каких значениях параметра a площадь фигуры, заданной системой неравенств

равна

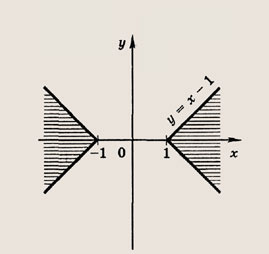
Преобразуем заданную систему:

Ответ: и

За каждый из четырех пунктов сюжета выставляется одна из следующих оценок:

+ (3 балла), ± (2 балла), ∓ (1 балл), − (0 баллов)

Максимум за сюжет 12 баллов. При этом необходимо руководствоваться следующим.

Критерии оценивания выполнения заданийБаллыВерное и полное выполнение задания3Ход решения верный, решение доведено до ответа, но допущен один недочет2Ход решения верный, решение доведено до ответа, но допущено два недочета или одна грубая ошибка1Остальные случаи0

К недочетам относятся, например: описки, неточности в использовании математической символики; погрешности на рисунках, недостаточно полные обоснования; неточности в логике рассуждений при сравнении чисел, доказательстве тождеств или неравенств; вычислительные ошибки, не повлиявшие принципиально на ход решения и не упростившие задачу, если задача не являлась вычислительной; замена строго знака неравенства нестрогим или наоборот; неверное присоединение либо исключение граничной точки из промежутка монотонности и аналогичные.

Грубыми ошибками являются, например: потеря или приобретение постороннего корня; неверный отбор решения на промежутке при правильном решении в общем виде; вычислительная ошибка в задаче на вычисление; неверное изменение знака неравенства при умножении на отрицательное число, логарифмировании или потенцировании и т. п.

Источник

При каких значениях параметра площадь фигуры заданной системой неравенств равна

ПАРАМЕТРЫ И НАХОЖДЕНИЕ ПЛОЩАДЕЙ ФИГУР

Автор работы награжден дипломом победителя III степени

Широко известно о применении интеграла к вычислению различных величин, об использовании для решения прикладных задач. Метод графического интегрирования основан на графическом подсчете определенного интеграла и заключается в последовательном нахождении площадей под соответствующей подынтегральной функции кривой. Он применяется для анализа электрических цепей, переходные процессы в которых описываются дифференциальными уравнениями первого порядка с разделяющимися переменными.

Цель работы: описать на языке математики особенности простых плоских фигур и их свойство-площадь, задаваемых с помощью различных линий и включающих в себя понятие параметра.

Составить и решить задачи, решаемые с помощью определенного интеграла, включающие в условии параметр.

Составить и решить задачи, решаемые с помощью определенного интеграла, включающие элементы оптимизации.

Использовать при решении задач свойства площадей фигур, свойства определенного интеграла.

ГЛАВА I. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

В задачах с параметрами наряду с неизвестными величинами фигурируют величины, численные значения которых хотя и не указаны конкретно, но считаются известными и заданными на некотором числовом множестве. При этом параметры, входящие в условие, существенно влияют на логический и технический ход решения и форму ответа.

В литературе по элементарной математике немало учебных пособий, задачников, методических руководств, где приводятся задачи с параметрами. Но большинство из них охватывает узкий круг вопросов. Задачи с параметрами в интегрировании встречаются крайне редко.

Определение. Если при существует конечный предел интегральных сумм, не зависящий от разбиения на части и от выбора точек в этих частях, то:

1) функция называется интегрируемой на отрезке;

Принятая терминология: отрезок – отрезок интегрирования, a иb – нижний и верхний пределы интегрирования, x – переменная интегрирования, – подынтегральная функция, – подынтегральное выражение.

Некоторые свойства определенного интеграла:

Постоянный множитель можно выносить за знак интеграла.

Интеграл от алгебраической суммы двух функций равен сумме интегралов от этих функций (верно для любого числа слагаемых).

Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей.

Определение. Параметром называется независимая переменная, значение которой в задаче считается задан­ным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренно­му множеству.

Что означает «решить задачу с параметром»?

Естественно, это зависит от вопроса в задаче. Если, например, требуется решить уравнение, неравенство, их систему или совокупность, то это означает предъявить обоснованный ответ либо для любого значения парамет­ра, либо для значения параметра, принадлежащего зара­нее оговоренному множеству.

Если же требуется найти значения параметра, при ко­торых множество решений уравнения, неравенства и т. д. удовлетворяет объявленному условию, то, очевидно, ре­шение задачи и состоит в поиске указанных значений параметра.

Определение интеграла, зависящего от параметра: интеграл называется интегралом, зависящим от параметра, если интегрируема на промежутке

ГЛАВА II. ПРАКТИЧЕСКАЯ ЧАСТЬ

Задачи, включающие элементы оптимизации.

Решение. Найдём точки пересечения графика функции с осью ОХ:

Определим абсциссу вершины параболы с помощью производной:

Раскроем знак модуля для заданной функции :

Рассмотрим два случая:

Задача 2.Найдите значение а при котором фигура, ограниченная параболамиимеет наибольшую площадь.

Найдём точки пересечения заданных парабол:

Рассмотрим расположение графиков функций (Рис. 1):

Составим формулу для вычисления площади заштрихованной фигуры:

Исследуем знак производной при (Рис. 2):

_{Задачи, решаемые с помощью свойств площадей фигур, свойств определенного интеграла.}

_{Задача 3}. Найти площадь фигуры, если известно, что она ограничена графиками функций, производной второй функции принадлежит точка с координатами

Найдем координаты точек пересечения параболы с прямой:

_{Вычислим координаты вершины параболы:}

Изобразим схематически графики заданных функций (Рис. 3):

Вычислим площадь заданной фигуры:

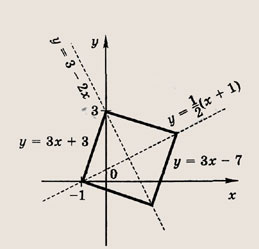
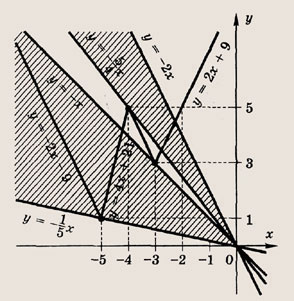
_{Задача 4. Фигура ограничена линиями} Чемуравен угловой коэффициент прямых, проходящих через точку(0; 0) и разбивающих фигуру на три равновеликие части?

_{Решение. Выполним построения, соответствующие условию задачи (Рис. 4)}

_{Определим угловые коэффициенты прямых, используя формулу площади прямоугольного треугольника}

Решение. Изобразим схематически заданные линии (Рис. 5):

Найдём точки пересечения параболы и прямой (Рис. 6):

ЗАКЛЮЧЕНИЕ

Составлено 7 задач, решаемых с помощью определенного интеграла, включающие в условии параметр, из них две задачи включали элементы оптимизации, пять задач решались с помощью свойства площадей фигур, свойства определенного интеграла.

Проведенное занятие убедило выпускников школы в необходимости более глубокого изучения интегральных вычислений, включая интегралы с параметром.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ И ЛИТЕРАТУРЫ

Метод графического интегрирования- Режим доступа: StudFiles.ru›preview/4416561/ (дата обращения 8.07.2017)

Журнал Математика в школе №4, 1992. С. 25-27

Свойства определенного интеграла — Студопедия— Режим доступа:studopedia.ru›18_63510_svoystva…integrala.html (дата обращения 8.07.2017)

Амелькин В.В. Задачи с параметрами: Справ. Пособие по математике.-2-ое изд./ Рабцевич В.Л.– Мн.: ООО Асар, 2002. –5 с.

Математика: Учебник для XII класса / И. Акири, В. Гарит, П. Ефрос и др. – Кишинёв, Prut International, 2005.- 34 с.

Моденов В.П. Задачи с параметрами. Координатно-параметрический метод: Учебное пособие для школьников и абитуриентов. – М.: Издательство Экзамен, 2007.

Старт в науке

Учредителями Конкурса являются Международная ассоциация учёных, преподавателей и специалистов – Российская Академия Естествознания, редакция научного журнала «Международный школьный научный вестник», редакция журнала «Старт в науке».

Источник

Вычисление площади фигуры, ограниченной параметрически заданной кривой

После объяснения теории и выведения формулы мы разберем несколько характерных примеров на нахождение площади таких фигур.

Основная формула для вычисления

Мы вывели ее из формулы площади криволинейной трапеции S ( G ) = ∫ a b f ( x ) d x методом подстановки x = φ ( t ) y = ψ ( t ) :

S ( G ) = ∫ a b f ( x ) d x = ∫ α β ψ ( t ) d ( φ ( t ) ) = ∫ α β ψ ( t ) · φ ‘ ( t ) d t

Если функция x = φ ( t ) не относится к основным элементарным, то нам понадобится вспомнить основные правила возрастания и убывания функции на интервале, чтобы определить, будет ли она возрастающей или убывающей.

Решение задач на вычисление площади фигуры, которая ограничена параметрически заданной кривой

В этом пункте мы разберем несколько задач на применение формулы, выведенной выше.

Решение

Вот ход наших вычислений:

Ответ: S ( G ) = 6 π

После этого вычисляем площадь половины эллипса:

Важно отметить, что можно взять только верхнюю или нижнюю часть, а правую или левую нельзя.

Разберем еще одну задачу.

Решение

Теперь разберем подробно, как построить такую кривую. Выполним построение по отдельным точкам. Это самый распространенный метод, который применим для большинства задач. Более сложные примеры требуют проведения дифференциального исчисления, чтобы выявить параметрически заданную функцию.

Составим таблицу итоговых значений:

После этого отметим нужные точки на плоскости и соединим их одной линией.

Теперь нам надо найти площадь той части фигуры, что находится в первой координатной четверти. Для нее x ∈ a ; b = 0 ; 3 :

Источник

При каких значениях параметра площадь фигуры заданной системой неравенств равна

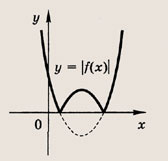
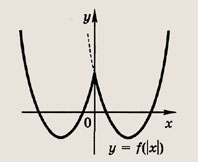
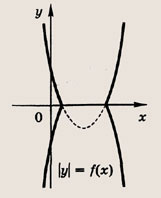
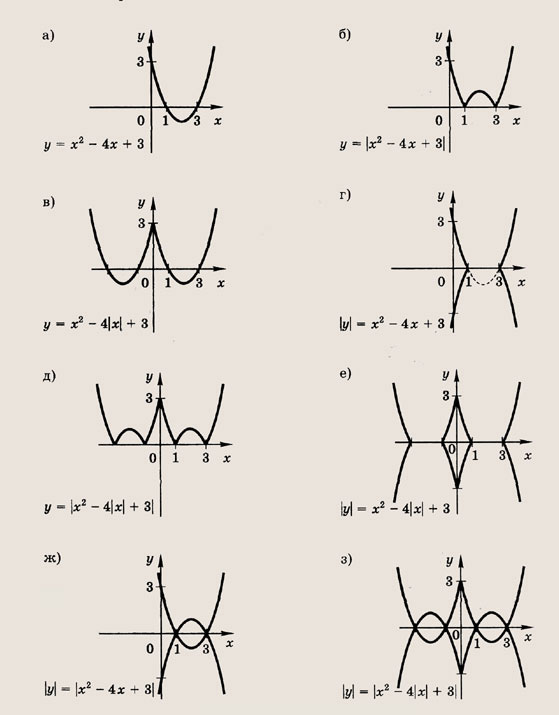
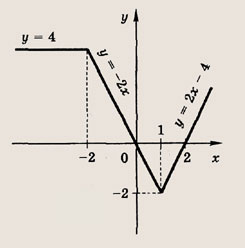
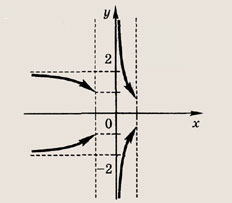
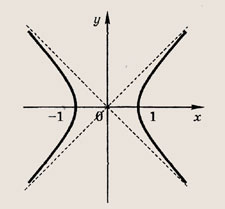
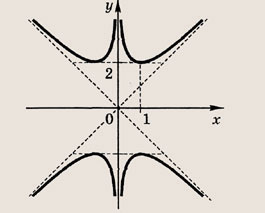
Модуль величины. Графики выражений, содержащих модули

• Модулем числа а называется величина, обозначаемая |а| и такая, что

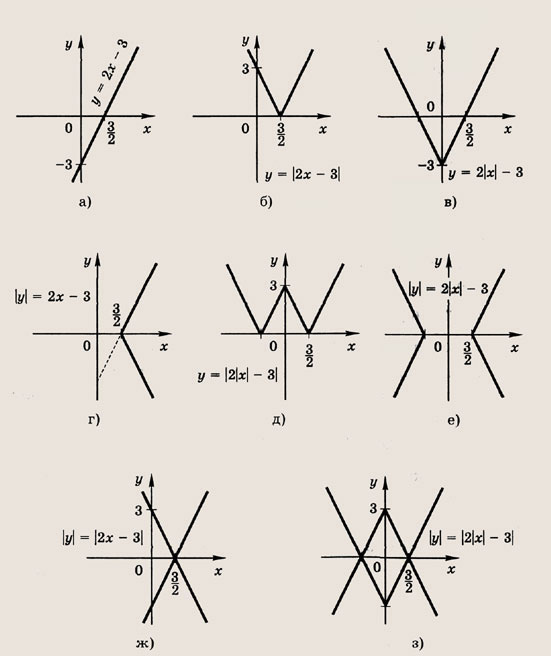
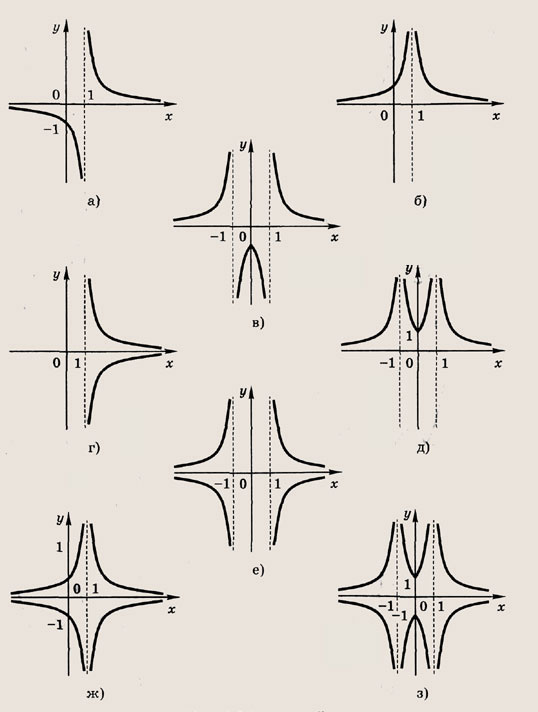
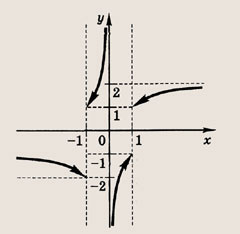
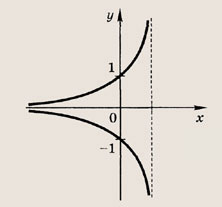
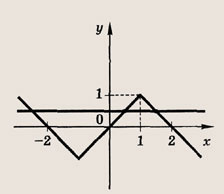
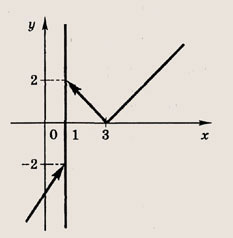
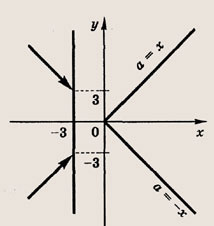
Графики функции у = f(x) и этих выражений приведены ниже.

Графики соотношений, содержащих большее число знаков модуля, строим, последовательно выполняя приведенные выше построения.

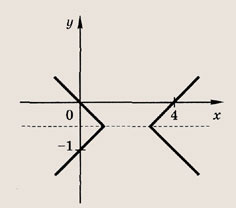
В заданиях 1—6 постройте графики следующих функций и уравнений:

Задание 1.

Ответ:

Задание 2.

Задание З.

Ответ:

Задание 4.

Задание 5.

Ответ:

Задание 6.

Ответ:

Постройте графики следующих функций и уравнений (7-26):

Задание 7.

Ответ:

Задание 8.

Ответ:

Задание 9.

Ответ:

Задание 10.

Ответ:

Задание 11.

Ответ:

Задание 12.

Ответ:

Задание 13.

Ответ:

Задание 14.

Ответ:

Задание 15.

Ответ:

Задание 16.

Ответ:

Задание 17.

Ответ:

Задание 18.

Ответ:

Задание 19.

Ответ:

Задание 20.

Ответ:

Задание 21.

Ответ:

Задание 22.

Ответ:

Задание 23.

Ответ:

Задание 24.

Ответ:

Задание 25.

Ответ:

Задание 26.

Ответ:

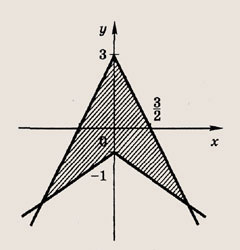
На координатной плоскости отметьте штриховкой множество точек, координаты которых удовлетворяют следующим неравенствам (27—40):

Задание 27.

Ответ:

Задание 28.

Указание:

Выполните параллельный перенос фигуры, построенной в задании 27.

Задание 29.

Ответ:

Задание 30.

Указание:

Выполните параллельный перенос фигуры, построенной в задании 29.

Задание 31.

Ответ:

Задание 32.

Ответ:

Задание 33.

Ответ:

Задание 34.

Ответ:

Задание 35.

Ответ:

Задание 36.

Ответ:

Задание 37.

Ответ:

Задание 38.

Ответ:

Задание 39.

Ответ:

Задание 40.

Указание:

Выполните параллельный перенос фигуры, построенной в задании 39.

Найдите площадь фигуры, которая задается на координатной плоскости следующими соотношениями (41—46).

Задание 41.

Ответ:

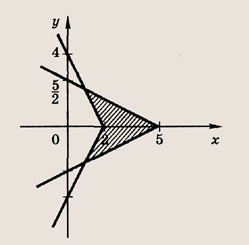
Задание 42.

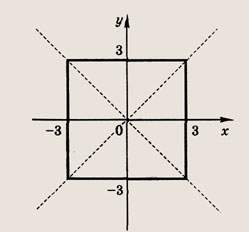
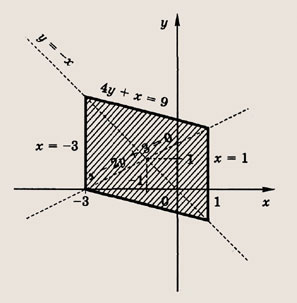
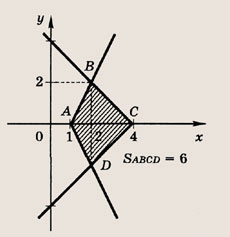
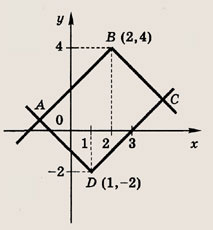
Фигура, определяемая заданными неравенствами, — прямоугольник ABCD

Ответ:

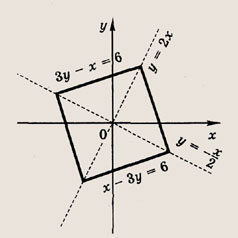
Задание 43.

Указание:

Ответ:

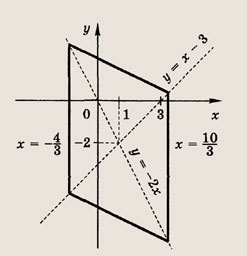
Задание 44.

Ответ:

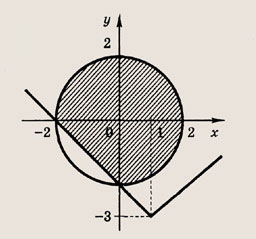
Задание 45.

Решение:

Запишем данное равенство в виде

Это равенство справедливо только в том случае, если пара чисел (х; у) удовлетворяет одной из следующих систем неравенств:

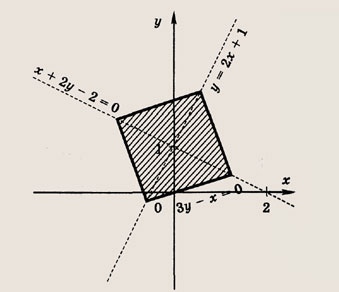
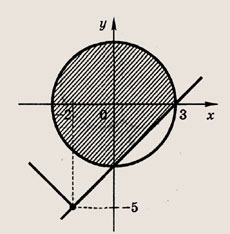
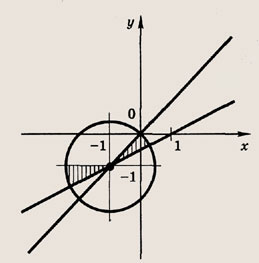
Отметим штриховкой в плоскости (х ; у) множество точек, координаты которых удовлетворяют этим неравенствам, а также неравенству

Мы видим, что площадь заштрихованной области равна

площади круга радиуса

Следовательно, искомая площадь равна

Ответ:

Задание 46.

Указание:

См. решение задания 45.

Ответ:

Задание 47.

При каких значениях р площадь фигуры, заданной на координатной плоскости условием

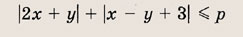
равна 24?

Решение:

Очевидно, что р > 0. Перепишем неравенство в виде

и выполним замену переменных, полагая

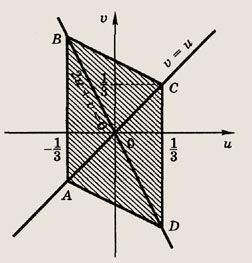
Построим фигуру, задаваемую в плоскости переменных (u; v) неравенством

и найдем ее площадь

Легко установить, что это параллелограмм. Сторона DC параллельна координатной оси Оv и равна по длине 1. Высота параллелограмма равна

получается из построенной растяжением вдоль обеих осей в р раз. Следовательно, ее площадь

Таким образом, и площадь фигуры, задаваемой неравенством

поскольку она получается параллельным переносом из фигуры

Теперь вычисляем требуемое значение

Ответ:

Задание 48.

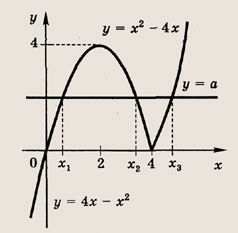
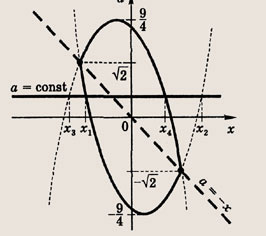
Найдите площадь фигуры, которая задается на координатной плоскости системой неравенств

При каких значениях а эта площадь является наибольшей?

Решение:

Эти неравенства задают непустое множество лишь при выполнении условия

Ответ:

Задание 49.

При каких значениях а система

имеет хотя бы одно решение?

Ответ:

Задание 50.

При каких значениях а система

имеет хотя бы одно решение?

Указание:

Постройте графики данных уравнений и проследите, как меняется график первого уравнения при изменении параметра а.

Ответ:

Решите следующие уравнения и системы уравнений (51—66):

Задание 51.

Ответ:

Задание 52.

Ответ:

Задание 53.

Ответ:

Задание 54.

Решение:

Раскрывая знак модуля, получаем на каждом из указанных ниже интервалов:

откуда получаем, что

Ответ:

Задание 55.

Указание:

См. решение задания 56.

Ответ:

Задание 56.

Данное уравнение равносильно совокупности двух систем:

Для первой из них записываем равносильную совокупность двух систем:

Решив эти системы, получаем

Аналогично вторая система равносильна следующей совокупности:

Ответ:

Задание 57.

Ответ:

Задание 58.

Ответ:

Задание 59.

Решение:

Запишем уравнение в виде

Раскрывая знак модуля на каждом из указанных ниже интервалов, получаем:

Однако оба эти корня не удовлетворяют условию х

В ответ войдет только значение

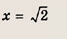
3)

Ответ:

Задание 60.

Ответ:

Задание 61.

Указание:

х = 0 не входит в область допустимых значений.

Ответ:

Задание 62.

Указание:

х = 1 не входит в область допустимых значений.

Ответ:

Задание 63.

Ответ:

Задание 64.

Решение:

3|х + 1| + х = 20, откуда следует:

х > 0 ==> Зх + 3 + х = 20, т. е.

Ответ:

Задание 65.

Ответ:

Задание 66.

Решение:

Данная система равносильна совокупности

Ответ:

Задание 67.

Решение:

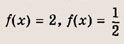
Далее, используя условие, получим

Теперь решаем уравнения:

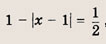
откуда

Эти решения будут повторяться с периодом, равным 4.

Ответ:

Задание 68.

2f(x + 4)f(x) + 5f(x + 16) + 2 = 0

Указание:

См. решение задания 67.

Ответ:

Задание 69.

Решение:

Данное уравнение равносильно совокупности двух следующих систем:

Решение первой системы дает:

Объединяя решения, получаем ответ.

Ответ:

Задание 70.

Ответ:

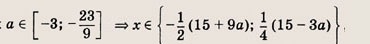
при

Задание 71.

При всех значениях а решите уравнение

Ответ:

Указание:

Далее см. решение задачи 69.

Задание 72.

При всех значениях а решите уравнение

Ответ:

При решении задач 73—76 используйте следующие простые неравенства, справедливые для любых чисел и и v:

Подумайте, когда выполняются равенства?

Задание 73.

Найдите все а, при которых среди решений уравнения

имеется ровно одно целое число.

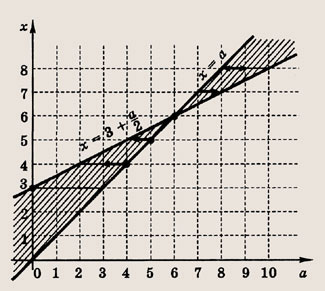
Решение:

Отметим в плоскости (а, х) штриховкой область, в которой выполняются эти неравенства.

Мы видим, что при а = б уравнение имеет в качестве целочисленного решения только число х = 6. Далее находим, что

и т. д., а также

и т. д. Единственное целое решение уравнение будет иметь лишь при

Ответ:

Задание 74.

Найдите все а, при которых среди решений неравенства

имеются ровно два натуральных числа.

Указание:

Ответ:

Задание 75.

При каких а система уравнений

имеет хотя бы одно решение?

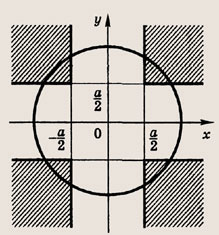
Решение:

Для выполнения первого равенства необходимо, чтобы

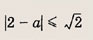
откуда

При этих значениях а график первого уравнения — окружность с центром О(0; 0) и радиусом

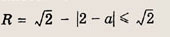
Обозначив

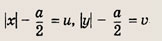
запишем второе уравнение в виде |u| + |v| = u + v. Последнее равенство справедливо только при

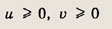
т. е. при

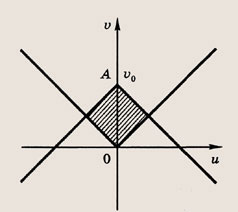
Отметим в плоскости (х; у) штриховкой эту область.

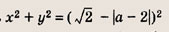
пересекает с заштрихованной областью (т.е. исходная система имеет решения) при выполнении неравенства

Это неравенство выполняется лишь при а = 2, поскольку

это число и является решением.

Ответ:

Задание 76.

При каких а система неравенств

имеет хотя бы одно решение?

Указание:

Первое неравенство справедливо только в том случае, если

Далее рассмотрите отдельно случай

При а > 0 решение аналогично решению задания 75.

Ответ:

• Использование графических методов (построение графиков, штриховка областей, отвечающих условиям задач) существенно облегчает решение приведенных ниже задач.

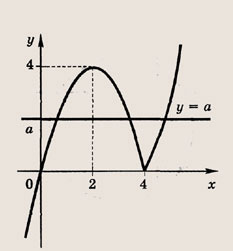
Установите, сколько решений в зависимости от а имеют следующие уравнения (77—84):

Задание 77.

Ответ:

четыре решения; при а = 2 => три решения.

Задание 78.

Ответ:

нет решений, при а = 1 => одно решение; при

Задание 79.

Решение:

График этой функции изображен на рис.

Ответ:

Задание 80.

Решение:

Ответ:

Задание 81.

Ответ:

Задание 82.

Решение:

Запишем уравнение в виде

Построим ее график

Ответ:

четыре решения; при

два решения; при а = 4 => три решения; при

четыре решения; при

Задание 83.

Ответ:

нет решений; при а = 2 => два решения; при

Задание 84.

Ответ:

нет решений; при а = 0 => одно решение; при

Задание 85.

Ответ:

Задание 86.

Решение:

Штриховкой отметим те углы, в которых прямая у = ах пересекает построенный график ровно в двух точках.

Ответ:

Задание 87.

Решение:

Рассмотрим два случая.

Объединяя все решения, записываем ответ:

Ответ:

Задание 88.

При каких значениях а уравнение

имеет ровно три различных решения?

Решение:

Запишем уравнение в виде

и построим график левой части этого уравнения.

Ответ:

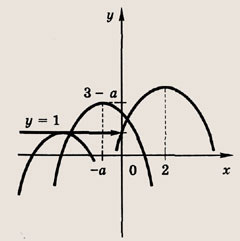
Задание 89.

При каких а система уравнений

имеет единственное решение?

Решение:

Точка пересечения графиков будет единственной, если

либо у(-а) = 1. Неравенство

Ответ:

Задание 90.

При каких а система уравнении

имеет хотя бы одно решение?

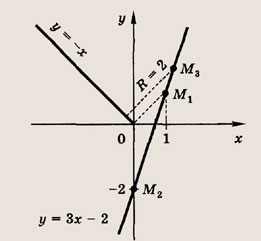
Решение:

(х- а) 2 + (-х- За + 2) 2 =4

должно иметь единственное решение. Раскрывая скобки и приводя подобные члены, приравнивая дискриминант квадратного трехчлена нулю, получаем

Следует взять положительное значение а, т. е.

Легко видеть, что точка М₂ получается при а = 0.

Ответ:

Задание 91.

При каких а уравнение

имеет единственное решение?

Ответ:

Решите следующие уравнения (92—98):

Задание 92.

Ответ:

Задание 93.

Решение:

Ответ:

Задание 94.

Ответ:

Задание 95.

Указание:

Ответ:

Задание 96.

Решение:

Построим график этого уравнения.

Ответ:

Задание 97.

Решение:

Раскрывая модуль, получаем

Решим эти уравнения:

Ответ:

Задание 98.

Ответ:

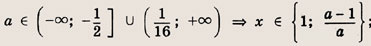
при

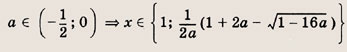
при

Источник