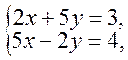при каком значении параметра прямая параллельна прямой

При каком значении параметра прямые параллельны?

При каком значении p прямые
x=2t+5
y=-t+2
z=pt-7
И
x+3y+z+2=0
x-y-3z-2=0
параллельные?

Добавлено через 26 минут
Помогите, пожалуйста

Помощь в написании контрольных, курсовых и дипломных работ здесь.

При каком значении параметра векторы перпендикулярны?
При каком значении a векторы AB,AC где A(2;3;a), B(-1;3;-2), C(3;-7;-3), перпендикулярны?

Добавлено через 41 секунду
Почитайте в Интернете про способы задавания прямых и условие параллельности.

Добавлено через 3 минуты
В интернете искал не нашел

Добавлено через 28 минут
FFPowerMan, помогите пожалуйста

Добавлено через 32 секунды

Помощь в написании контрольных, курсовых и дипломных работ здесь.

При каком значении параметра а точки не лежат на одной окружности?
А(-1;5) В(-2;-2) С(1;а) Знаю только теорему о том, когда точки лежат на одной прямой. На.

Прямая а и с параллельны, а прямые а и b пересекаются.Могут ли прямые b и с быть скрещивающимися?
Прямая а и с параллельны, а прямые а и b пересекаются.Могут ли прямые b и с быть скрещивющимися?

Доказать что прямые параллельны
Даны две плоскости альфа и бета пересекающиеся по прямой а, прямая b параллельна плоскостям и не.

Источник

Кстати, последнее неравенство как раз и говорит о непараллельности их нормальных векторов.

Если прямые параллельны, то система решения не имеет. Аналитически это будет выглядеть так:

.

Но если все три дроби равны, то прямые совпадают друг с другом, и поэтому система имеет бесконечное множество решений.

Угол между двумя прямыми можно найти по двум формулам.

Если прямые заданы общими уравнениями, то угол между ними совпадает с углом между их нормальными векторами. Его вычисляют по формуле (6.9) из предыдущей лекции. Для нашего случая она будет иметь вид:

. (7.7)

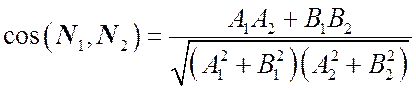
Условие параллельности прямых:

;

.

Если прямые заданы уравнениями с угловыми коэффициентами вида:

и ,

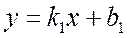
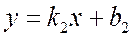
то тангенс угла между ними определится по формуле:

. (7.8)

.

.

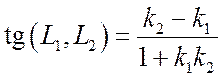
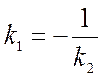
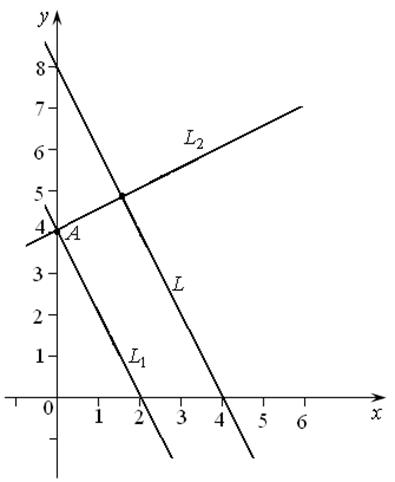
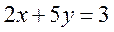
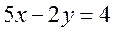
Пример 7.4. Найти точку пересечения прямых и и угол между ними.

Решение.Найдем точку пересечения прямых, решив систему уравнений методом Крамера:

, , ,

, .

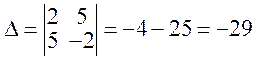
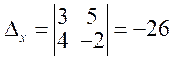
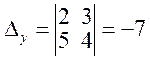
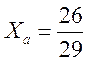
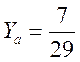
Угол между прямыми определим, как угол между их нормальными векторами (2, 5) и (5, –2). По формуле (7.7) имеем:

.

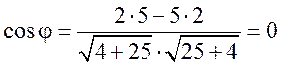
О чем говорит этот ответ? Прямые перпендикулярны, т.к. .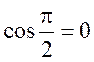

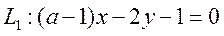
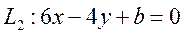
Пример 7.5. При каком значении параметров a и b прямые и : а) пересекаются, б) параллельны, в) совпадают?

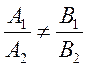
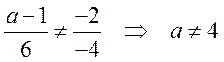
Решение.Две прямые пересекаются, если выполняется условие . В нашем случае

.

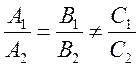
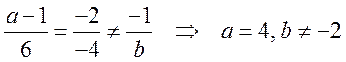
Прямые параллельны, если , т.е.

.

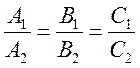
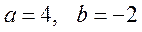
И, последнее, две прямые совпадают при условии, что , т.е. если .

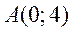
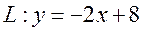
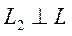
Пример 7.6. Дана точка и прямая . Написать уравнения прямых L₁ и L₂, проходящих через точку A, причем и .

Угловой коэффициент исходной прямой L равен k = –2. По условию , следовательно . По формуле (7.4) находим уравнение прямой L₁:

, или .

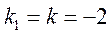
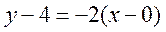
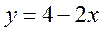
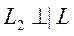
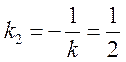
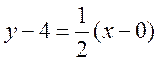
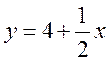
Поскольку , то . Тогда уравнение прямой L₂ будет иметь вид:

, или .

7.4. Определение кривой второго порядка

Определение 7.1. Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих координат. В общем случае это уравнение имеет вид:

, (7.9)

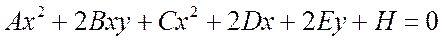
где все числа А, В, С, и т.д. – действительные числа, и, кроме того, по крайней мере одно из чисел А, В, С – отлично от нуля.

До введения декартовой системы координат все кривые описывались словесно, исходя из геометрических свойств рассматриваемой кривой. Так, определение окружности читалось так:

Определение 7.2. Окружность – это геометрическое место точек на плоскости, равноудаленных от данной точки, называемой центром.

Уравнение окружности, с центром в точке (а, b) и радиусом R в декартовой системе координат, полученное вами в школе, выглядит так:

. (7.10)

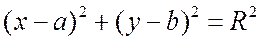
Если раскрыть скобки, то получим уравнение, схожее с уравнением (7.9), в котором отсутствует член, содержащий произведение текущих координат, и коэффициенты при старших степенях равны между собой.

Вывод всех уравнений второго порядка аналогичен выводу уравнений прямой и проходит по тому же алгоритму.

Выведем уравнение параболы, исходя из ее определения.

7.5. Каноническое уравнение параболы

Определение 7.3. Параболой называется геометрическое место точек плоскости, равноудаленных от данной точки F, называемой фокусом, и данной прямой, называемой директрисой.

Обозначим расстояние от фокуса до директрисы через p. Эта величина называется параметром параболы.

1. Расположим ось абсцисс так, чтобы она проходила через фокус, перпендикулярно директрисе и имела положительное направление от директрисы к фокусу.

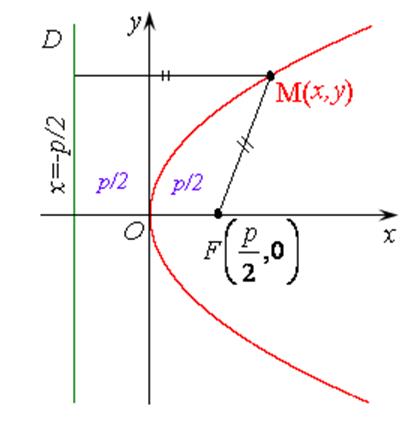
2. Начало координат поместим в середину этого перпендикуляра. Тогда координаты точки будут F(p/2, 0), а уравнение директрисы: .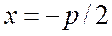

3. Возьмем текущую точку на параболе М(х, у).

4. По определению параболы, расстояние МN от точки М до директрисы равно ее расстоянию МFот фокуса: MF= MN. Как видно из чертежа (рис. 7.7), координаты точки N(–p/2, y). Найдем эти расстояния по формуле расстояния между двумя точками из п. 1 предыдущей лекции.

, .

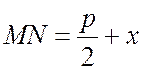
Приравняв правые части этих выражений и возведя обе части равенства в квадрат, получим:

,

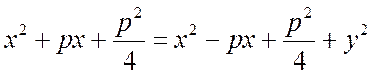
или после сокращений

. (7.11)

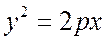
Уравнение (7.11) называется каноническим уравнением параболы. Ему будут удовлетворять только точки, лежащие на кривой, а остальные – не будут. Исследуем форму ее графика по каноническому уравнению.

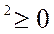
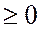
Поскольку y входит в четной степени, то ось ОХ будет являться осью симметрии, т.е. одному значению Х будет соответствовать два значения Y – положительное и отрицательное. Т.к. правая часть неотрицательна у, то и левая – тоже. Так как р – расстояние между фокусом и директрисой, всегда больше нуля, то и х. Если х=0, то у=0, т.е. парабола проходит через начало координат. При неограниченном возрастании x абсолютная величина у также будет неограниченно возрастать.

График параболы, определяемой уравнением (7.11) приведен на рис. 7.7.

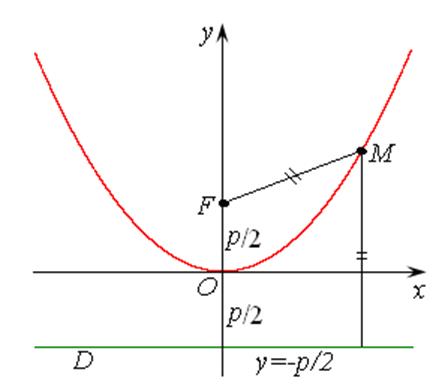
Ось симметрии параболы называется фокальной осью, т.к. на ней лежит фокус. Если фокальную ось параболы принять за ось ординат, то ее уравнение примет вид:

.

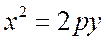
Ее чертеж показан на рис. 7.8. В этом случае фокус будет находиться в точке F(0, p/2), а уравнение директрисы будет иметь вид у = –р/2.

Таким образом, мы рассмотрели параболу, нашли ее уравнение и показали возможные расположения относительно начала координат.

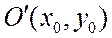
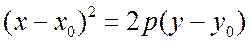
Если вершина параболы смещена в точку , то каноническое уравнение будет выглядеть так:

.

Выводом остальных кривых второго порядка мы заниматься не будем. Желающие могут найти все выкладки в рекомендуемой литературе.

Ограничимся их определениями и уравнениями.

7.6. Каноническое уравнение эллипса

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Факультативный курс «Линейные уравнения и неравенства с параметрами»

Линейной называется функция, задаваемая уравнением вида y = kx + b, где x — независимая переменная или аргумент, а k и b — произвольные действительные числа. Графиком линейной функции является прямая. Задавая конкретные значения параметров, мы выделяем из множества линейных функций одну или несколько функций, обладающих тем или иным свойством. Множество функций, обладающих указанным свойством, называют семейством функций, а множество их графиков — семейством графиков (семейством прямых).
Упражнение 1. Каким общим свойством будут обладать все графики функций, задаваемых уравнениями вида y = kx – 1?
Упражнение 2. Из множества линейных функций выделите семейство графиков, задаваемых уравнениями вида y = 2x + p.
Итак, задавая значение параметра b, мы выделяем семейство линейных функций, графики которых проходят через точку (0; b). Задавая значение параметра k, мы выделяем семейство линейных функций, графики которых параллельны прямой y = kx.
Упражнение 3. При каком значении k график функции y = kx + 2 проходит через точку A(1; 4), а при каких через точку B(–2; 0)?
Упражнение 4. График функции y = kx + b проходит через точки A(0; –4) и B(3; 5). Найдите значения k и b.
Упражнение 5. График функции y = kx + b проходит через точку B(3; 5) и параллелен графику функции y = 2x. Найдите значения k и b.
Полезно напомнить, что параметр k называют угловым коэффициентом. Если угловые коэффициенты равны, то прямые или параллельны (при b 1 ≠ b 2 ), или совпадают (при b 1 = b 2 ); если угловые коэффициенты различны — прямые пересекаются.
Упражнение 6. При каких значениях параметра a графики данных функций пересекаются:
а) y = (2a – 1)x и y = (4a + 3)x + 2a;
б) y = ax + 6a и y = ax?
Упражнение 7. При каких значениях параметра a графики данных функций параллельны:
а) y = (3 – a)x + 1 и y = (a – 1)x + 5;
б) y = (a – 3)x + 2a и y = (3 – 2a)x + a;
в) y = (a – 2)x + 6 – a и y = (2a – 3)x + 2a + 3?
Упражнение 8. При каких значениях параметра a графики данных функций совпадают:
а) y = 2ax + 7 и y = 4ax + 7;
б) y = (5a – 3)x + 2a – 1 и y = (a + 1)x + 14 + a;
в) y = (5a – 3)x + 3a и y = (5a + 1)x + 3a?
Упражнение 9. Проанализируйте, как изменяется наклон прямой в зависимости от параметра k, на примере функции y = kx (прямая пропорциональность).

Задание на дом
1. При каких значениях параметра a прямые y = –ax + 2 и будут: пересекаться, совпадать, параллельны?
2. Найдите значения параметра a, при которых прямая y = ax + 2 пройдет через точку пересечения прямых y = 5x – 7 и y = 3x + 1?
3. Постройте графики функций:
а) y = | x |; б) y = | x | + 1; в) y = | x + 1 |.

Упражнение 1. Постройте графики функций:
а) y = 1,5x – 2, где –2 ≤ x ≤ 2,
(график — отрезок);
б) y = 1,5x – 2, где x ≤ 2,
(график — луч, идущий влево,
с началом в точке (2; 1));
в) y = 1,5x – 2, где x ≥ –2,
(график — луч, идущий вправо,
с началом в точке (–2; –5)).

Упражнение 2. Постройте графики кусочно-заданных функций и графики функций, содержащих знак модуля:
а) в) y = | x | – 2;
б) г) y = | x – 2 | – 2.

Далее знакомим учащихся с понятиями «плавающей» и «вращающейся» прямых.

Упражнение 3. Постройте семейство прямых:
а) y = a;
б) y = ax.
Семейство прямых, задаваемых уравнением вида y = a — это прямые, параллельные оси абсцисс («плавающая» прямая). Семейство прямых, задаваемых уравнениями вида y = ax — это прямые, проходящие через начало координат («вращающаяся» прямая). Полезным будет вспомнить, что с увеличением a прямая вращается против часовой стрелки.

Упражнение 4. Сколько общих точек имеют графики функций из упражнения 2 и прямая
y = a в зависимости от значения параметра a?
Решение.

а) при a 3 — нет точек пересечения;
при 0 ≤ a 2 — нет точек пересечения;
при –2 –2 — две общие точки;

г) при a –2 — две общие точки.

Упражнение 5. Сколько общих точек имеют графики функций из упражнения 2 и прямая
y = ax в зависимости от значений параметра a?
Решение.

а) при a 1 — одна общая точка;
при 0 ≤ a 1 — одна общая точка;
при 0 2 – y = 0; б) x + y = 2?

Упражнение 2. Постройте графики уравнений:
а) | x – 2 | = 0; б) 2x + 4y = 1;
в) | x – 1 | + (y + 2) 2 = 0;
г) 2ax 2 – 3x 2 – 9y + 6ay = 0 при a = 1,5.
Ответ: а) прямая x = 2;
б) прямая y = –0,5x + 0,25;
в) точка (1; –2);
г) вся координатная плоскость.

Упражнение 3. Найдите все общие точки уравнений x 2 – y = 0 и x + y = 2.
Ответ: (–2; 4), (1; 1).
Далее знакомим учащихся с графическим способом решения уравнений с параметром. При этом рассматриваем уравнение с параметрами как уравнение с двумя неизвестными, график которого существует, но только в плоскости Oxa. Сначала рассмотрим уравнение, которое может быть решено как графически, так и аналитически. Далее — уравнение, аналитический способ решения которого явно громоздкий.

Упражнение 4. Решите уравнение
(| x | – 4)(x + 2a) = 0.
Решение. Уравнение (| x | – 4)(x + 2a) = 0 можно решить как аналитически, так и графически. Разберем оба способа.
Способ I (аналитический). В данном случае произведение равно 0, если один из множителей равен 0, то есть | x | – 4 = 0 или x + 2a = 0. Отсюда x = ±4 или x = –2a.
Если –2a = ±4, то есть a = ±2, то уравнение имеет два корня: x = ±4,
Если a ≠ ±2, то три корня: x = ±4 или x = –2a.
Способ II (графический). Построим график уравнения в системе координат Oxa.

График уравнения — прямые x = 4, x = –4 и a = –0,5x. Проводим горизонтальные прямые
a = α. В зависимости от α находим решения уравнения как абсциссы точек пересечения прямой a = α с графиком уравнения (ось ординат не y, а параметр a).
Ответ: при a = ±2 x = ±4;
при a ≠ ±2 x = ±4 и x = –2α

Упражнение 5. Решите уравнение
(x 2 – a 2 )(a – 1 – | x |) = 0.
Решение. Построим график уравнения
(x 2 – a 2 )(a – 1 – | x |) = 0
в системе координат Oxa. Это прямые a = x, a = –x и график функции a = | x | + 1. Проводим горизонтальные прямые a = α. В зависимости от α находим решения уравнения как абсциссы точек пересечения прямой a = α с графиком уравнения. Получаем, что при a 1 — четыре корня: x = ±a и x = ±a + 1.

Ответ: при a 1 = ±a и x = ±a + 1.
Обратим внимание учащихся на то, что графическим способом удобно находить количество решений уравнения с параметрами.

Упражнение 6. При каких значениях параметра a уравнение имеет ровно три корня?
Решение.

Графиком уравнения будут парабола a = x 2 и прямая x = –2. Необходимо также учесть область определения a ≠ x. Проводим горизонтальные прямые a = α и получаем, что уравнение будет иметь ровно три корня: при 0 4.

Ответ: при 0 4
уравнение имеет ровно три корня.

Задание на дом
1. Докажите, что уравнение
(a – | x – 1 |)(a + x 2 ) = 0
при любых значениях параметра a имеет два различных корня.
2. Постройте графики уравнений:
а) | x – 1 | + (x + y)2 = 0; б) x2 = 4y2;
в)
3. При каких значениях параметра a две прямые ax – y = –2a и x – ay = 2 будут пересекаться, совпадать или будут параллельны?

Одним из способов решения систем уравнений является графический способ.
Упражнение 1. Решите графически систему уравнений

Упражнение 2. При каких значениях параметра a система

имеет единственное решение?

Решение. Решим задание графически. Построим в одной системе координат графики уравнений, входящих в систему, то есть y = | x | – 4 и y = ax. Из рисунка видно, что графики будут иметь одну общую точку при a ≤ –1 или a ≥ 1.
Ответ: при a ≤ –1 или a ≥ 1 система имеет единственное решение.

Упражнение 3. При каких значениях параметра a система

имеет решения?
Решение. Графиком первого уравнения системы является пара точек на координатной плоскости: (1; 2) и (–1; 2). График второго уравнения — прямая y = 0,5ax – 1,5. Чтобы система имела решения, необходимо, чтобы прямая проходила через точки (1; 2) или (–1; 2). Подставляя координаты этих точек в уравнение прямой
y = 0,5ax – 1,5, получим:
0,5a – 1,5 = 2 или –0,5a – 1,5 = 2.
Откуда a = 7 или a = –7.
Ответ: при a = ±7 система имеет решения.
Линейным уравнением с двумя переменными называется уравнение вида ax + by = c, где
a 2 + b 2 > 0, то есть значение хотя бы одного из коэффициентов (параметров) должно быть отлично от нуля. Графиком линейного уравнения с двумя переменными является прямая линия.

Определение. Системой двух линейных уравнений с двумя переменными называется система вида

Определение. Решением системы двух линейных уравнений с двумя переменными называется упорядоченная пара значений этих переменных, обращающая в верное равенство каждое уравнение системы.
Так как каждому уравнению системы можно поставить в соответствие прямую, то решением системы будут являться координаты точек пересечения этих прямых.
Две прямые на плоскости могут быть параллельны, пересекаться или совпадать. В связи с этим и системы линейных уравнений могут иметь единственное решение, не иметь решений или иметь бесконечное множество решений. Для ответа на вопрос о количестве решений системы уравнений полезно заполнить с учащимися таблицу.

Алгоритм определения количества решений системы линейных уравнений

Упражнение 4. Найдите все значения параметра a, при каждом из которых система уравнений

не имеет решения.
Решение. Система не имеет решений, если выполняются условия

То есть должно быть

Отсюда a 2 = 4, a = ±2.
Если a = 2, то a 2 + a – 2 = 4, то есть что неверно.
Если a = –2, то a 2 + a – 2 = 0, то есть что верно.
Ответ: при a = –2 система не имеет решений.

Упражнение 5. Найдите все значения параметра a, при каждом из которых система уравнений

имеет бесконечно много решений.
Решение. Система имеет бесконечно много решений, если выполняются условия

Отсюда a 2 – 3a = 0, то есть a = 0 или a = 3.
Если a = 3, то — верно.
Если a = 0, то — неверно.
Ответ: при a = –3 система имеет бесконечно много решений.

Упражнение 6. Найдите все значения параметра a, при каждом из которых система уравнений

имеет единственное решение.
Решение. Система имеет единственное решение, если выполняется условие то есть

Отсюда a 2 ≠ 16, a ≠ ±4.
Ответ: при a ≠ ±4 система имеет единственное решение.

Упражнение 7. Для каждого значения параметра a определите число решений системы уравнений

Задание на дом
1. При каких значениях параметра a система

имеет:
а) одно решение;
б) бесконечно много решений;
в) не имеет решений?
2. Постройте графики уравнений:
а) | x – 1 | + (x + y) 2 = 0; б) x 2 = 4y 2 ;
в)
3. При каких значениях параметра a прямые ax – y = –2a и x – ay = 2 будут пересекаться, совпадать или будут параллельны?

Упражнение 1. Числа a и b таковы, что система уравнений

имеет единственное решение (1; 1). Найдите a и b.
Решение. Если x = 1, y = 1 — решение системы, то при подстановке данных значений в систему получаем:

Отсюда a = 1, b = –1 или a = –1 и b = 1. Система должна иметь единственное решение. Проверим, выполняется ли условие при найденных значениях параметров.
Если a = 1, b = –1, то — верно.
Если a = –1, b = 1, то — неверно.
Ответ: при a = 1 и b = –1 система имеет единственное решение.

Упражнение 2. Найдите все значения параметра b, при каждом из которых система уравнений

имеет бесконечное множество решений, причем одно из этих решений x = 1, y = 3.

Упражнение 3. При каких значениях параметров a и b равносильны системы уравнений

Решение. Системы уравнений равносильны, если имеют одинаковые множества решений. Графиком каждого уравнения этих систем является прямая, причем прямые второй системы пересекаются Значит, и прямые первой системы также должны пересекаться, причем в той же точке. Итак, все четыре прямые пересекаются в одной точке. Найдем эту точку, решив систему Решение системы — точка (3; 0). Подставив ее координаты 4

в уравнения с параметрами, получим: 3a = b + 1 и 6 = a 2 + 2. Откуда a = 2, b = 5
или a = –2, b = –7. Проверим, пересекаются ли уравнения первой системы при найденных значениях параметров, то есть выполняется ли условие
Если a = 2, b = 5, то условие не выполняется значит, найденные значения параметров не подходят.
Если a = –2, b = –7, то получим: что верно.
Ответ: при a = –2, b = –7 системы уравнений равносильны.

Упражнение 4. Решите систему уравнений

Упражнение 5. Решите систему уравнений

Решение. Выразим из второго уравнения переменную x и подставим в первое уравнение системы. Получим:

Преобразуем первое уравнение системы к виду: a(a + 3)y = –(a + 3). Допустимые значения переменных — любые числа. Коэффициент при y равен 0, если a = 0 или a = –3. При a = 0 получим уравнение 0жy = –3, которое не имеет корней. При a = –3 получим уравнение 0∙y = 0, которое имеет бесконечное множество корней, y— любое число. Если a ≠ 0 и a ≠ –3, то уравнение имеет единственный корень
Ответ: при a = 0 система не имеет решений;
при a = –3 x = 1 + 3y, y ∈ R;
при a ≠ 0 и a ≠ –3 x = 2,

Упражнение 6. При каких значениях параметра a система

имеет единственное решение? Найдите это решение.

Решение. Решим задачу графически. Построим графики уравнений системы в одной системе координат и по рисунку определим, при каких значениях параметра a графики имеют одну общую точку. y = | x + 2 | — прямой угол с вершиной в точке (–2; 0). y = ax + 1 — «вращающаяся» прямая, центр вращения — (0; 1). Чтобы определить угловой коэффициент прямой y = ax + 1, проходящей через вершину «угла», подставим ее координаты в уравнение прямой. Получим: –2a + 1 = 0, отсюда
a = 0,5. Если a ≤ –1, то абсциссу точки пересечения находим из уравнения x + 2 = ax + 1.
Отсюда
Аналогично при a > 1.
Ответ: при a ≤ –1 решение системы точка при a = 0,5 — точка (–2; 0); при
a > 1 — точка

Задание на дом
1. При каких значениях параметра p система уравнений

имеет решение?
2. При каких значениях параметра m система линейных уравнений

имеет одно решение, бесконечно много решений, не имеет решений?
3. Зная, что a < b, сравните:
а) 3a и 3b; б) –5a и –5b;
в) a – 4 и b – 4; г)
4. Верно ли, что если a < b, то:
а) a + 3 < b + 12; б) a – 6 < b – 2;
в) 2a < 2b + 2; г) –2a < –2b?

Источник