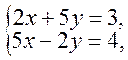при каком значении параметра прямая перпендикулярна прямой
Перпендикулярные прямые, условие перпендикулярности прямых
В статье рассматривается вопрос о перпендикулярных прямых на плоскости и трехмерном пространстве. Определение перпендикулярных прямых и их обозначения с приведенными примерами подробно разберем. Рассмотрим условия применения необходимого и достаточного условия перпендикулярности двух прямых и подробно рассмотрим на примере.
Перпендикулярные прямые – основные сведения
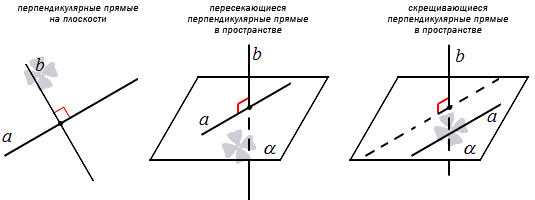
Угол между пересекающимися прямыми в пространстве может быть прямым. Тогда говорят, что данные прямые перпендикулярные. Когда угол между скрещивающимися прямыми прямой, тогда прямые также являются перпендикулярными. Отсюда следует, что перпендикулярные прямые на плоскости пересекающиеся, а перпендикулярные прямые пространства могут быть пересекающимися и скрещивающимися.
То есть понятия «прямые a и b перпендикулярны» и «прямые b и a перпендикулярны» считаются равноправными. Отсюда и взялось понятие взаимно перпендикулярные прямые. Обобщив вышесказанное, рассмотрим определение.
Две прямые называют перпендикулярными, если угол при их пересечении дает 90 градусов.
Перпендикулярность прямых – условия перпендикулярности
Свойства перпендикулярности необходимо знать, так как большинство задач сводится к его проверке для последующего решения. Бывают случаи, когда о перпендикулярности идет речь еще в условии задания или когда необходимо пользоваться доказательством. Для того, чтобы доказать перпендикулярность достаточно, чтобы угол между прямыми был прямым.
Для того, чтобы определить их перпендикулярность при известных уравнениях прямоугольной системы координат, необходимо применить необходимое и достаточное условие перпендикулярности прямых. Рассмотрим формулировку.
Само доказательство основывается на определении направляющего вектора прямой и на определении перпендикулярности прямых.
Очевидно, что необходимое и достаточное условие выполнимо, значит, А В и А С перпендикулярны.
Ответ: прямые перпендикулярны.
Решение
Результат произведения не равен нулю, можно сделать вывод, что векторы не перпендикулярны, значит и прямые также не перпендикулярны.
Ответ: прямые не перпендикулярны.
Векторы перпендикулярны, так как произведение равно нулю. Необходимое и достаточное условие выполнено, значит прямые также перпендикулярны.
Ответ: прямые перпендикулярны.
Проверка перпендикулярности может проводится, исходя из других необходимых и достаточных условий перпендикулярности.
Необходимое и достаточное условие было выполнено.
Ответ: прямые перпендикулярны.
Ответ: заданные прямые перпендикулярны.
Имеется еще одно условие, используемое для определения перпендикулярности прямых на плоскости.
Для перпендикулярности прямых a и b на плоскости необходимым и достаточным условием является коллинеарность направляющего вектора одной из прямых с нормальным вектором второй прямой.
Условие применимо, когда есть возможность нахождения направляющего вектора одной прямой и координат нормального вектора другой. Иначе говоря, одна прямая задается каноническим или параметрическим уравнением, а другая общим уравнением прямой, уравнением в отрезках или уравнением прямой с угловым коэффициентом.
Кстати, последнее неравенство как раз и говорит о непараллельности их нормальных векторов.
Если прямые параллельны, то система решения не имеет. Аналитически это будет выглядеть так:

Но если все три дроби равны, то прямые совпадают друг с другом, и поэтому система имеет бесконечное множество решений.
Угол между двумя прямыми можно найти по двум формулам.
Если прямые заданы общими уравнениями, то угол между ними совпадает с углом между их нормальными векторами. Его вычисляют по формуле (6.9) из предыдущей лекции. Для нашего случая она будет иметь вид:
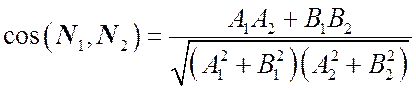
Условие параллельности прямых:


Если прямые заданы уравнениями с угловыми коэффициентами вида:
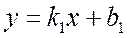
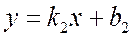
то тангенс угла между ними определится по формуле:
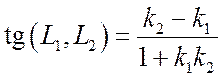

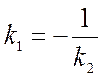
Пример 7.4. Найти точку пересечения прямых 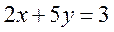
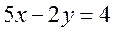
Решение.Найдем точку пересечения прямых, решив систему уравнений методом Крамера:
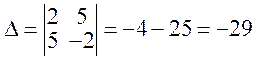
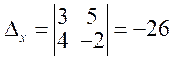
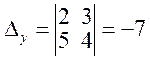
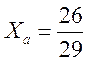
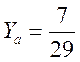
Угол между прямыми определим, как угол между их нормальными векторами (2, 5) и (5, –2). По формуле (7.7) имеем:
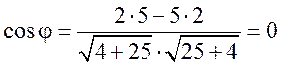
О чем говорит этот ответ? Прямые перпендикулярны, т.к. 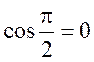
Пример 7.5. При каком значении параметров a и b прямые 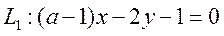
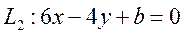
Решение.Две прямые пересекаются, если выполняется условие 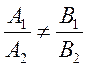
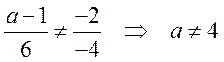
Прямые параллельны, если 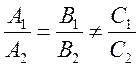
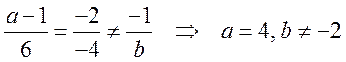
И, последнее, две прямые совпадают при условии, что 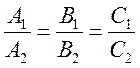
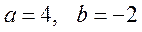
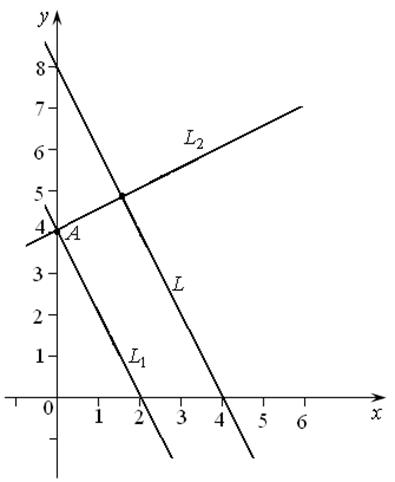
Пример 7.6. Дана точка 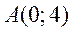
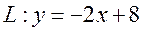

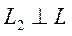
Угловой коэффициент исходной прямой L равен k = –2. По условию 
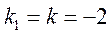
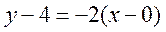
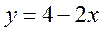
Поскольку 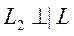
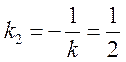
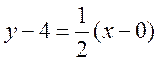
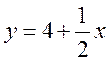
7.4. Определение кривой второго порядка
Определение 7.1. Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих координат. В общем случае это уравнение имеет вид:
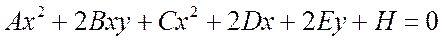
где все числа А, В, С, и т.д. – действительные числа, и, кроме того, по крайней мере одно из чисел А, В, С – отлично от нуля.
До введения декартовой системы координат все кривые описывались словесно, исходя из геометрических свойств рассматриваемой кривой. Так, определение окружности читалось так:
Определение 7.2. Окружность – это геометрическое место точек на плоскости, равноудаленных от данной точки, называемой центром.
Уравнение окружности, с центром в точке (а, b) и радиусом R в декартовой системе координат, полученное вами в школе, выглядит так:
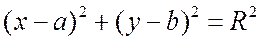
Если раскрыть скобки, то получим уравнение, схожее с уравнением (7.9), в котором отсутствует член, содержащий произведение текущих координат, и коэффициенты при старших степенях равны между собой.
Вывод всех уравнений второго порядка аналогичен выводу уравнений прямой и проходит по тому же алгоритму.
Выведем уравнение параболы, исходя из ее определения.
7.5. Каноническое уравнение параболы
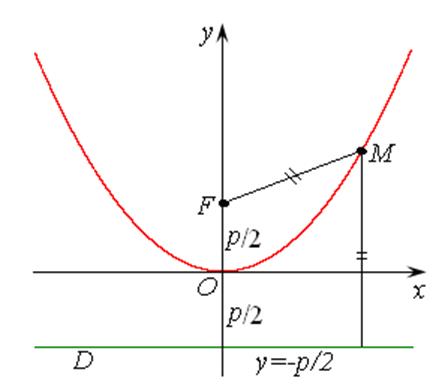
Определение 7.3. Параболой называется геометрическое место точек плоскости, равноудаленных от данной точки F, называемой фокусом, и данной прямой, называемой директрисой.
Обозначим расстояние от фокуса до директрисы через p. Эта величина называется параметром параболы.
1. Расположим ось абсцисс так, чтобы она проходила через фокус, перпендикулярно директрисе и имела положительное направление от директрисы к фокусу.
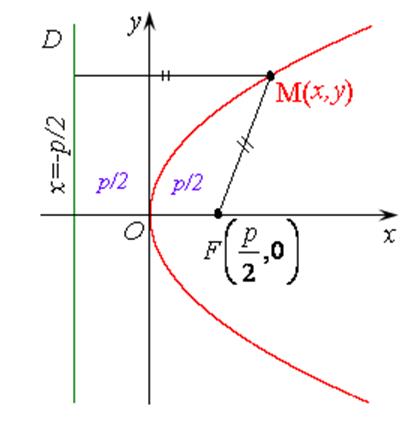
2. Начало координат поместим в середину этого перпендикуляра. Тогда координаты точки будут F(p/2, 0), а уравнение директрисы: 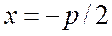
3. Возьмем текущую точку на параболе М(х, у).
4. По определению параболы, расстояние МN от точки М до директрисы равно ее расстоянию МFот фокуса: MF= MN. Как видно из чертежа (рис. 7.7), координаты точки N(–p/2, y). Найдем эти расстояния по формуле расстояния между двумя точками из п. 1 предыдущей лекции.
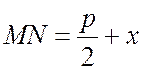

Приравняв правые части этих выражений и возведя обе части равенства в квадрат, получим:
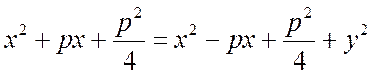
или после сокращений
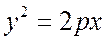
Уравнение (7.11) называется каноническим уравнением параболы. Ему будут удовлетворять только точки, лежащие на кривой, а остальные – не будут. Исследуем форму ее графика по каноническому уравнению.
Поскольку y входит в четной степени, то ось ОХ будет являться осью симметрии, т.е. одному значению Х будет соответствовать два значения Y – положительное и отрицательное. Т.к. правая часть неотрицательна у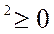
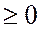
График параболы, определяемой уравнением (7.11) приведен на рис. 7.7.
Ось симметрии параболы называется фокальной осью, т.к. на ней лежит фокус. Если фокальную ось параболы принять за ось ординат, то ее уравнение примет вид:
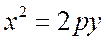
Ее чертеж показан на рис. 7.8. В этом случае фокус будет находиться в точке F(0, p/2), а уравнение директрисы будет иметь вид у = –р/2.
Таким образом, мы рассмотрели параболу, нашли ее уравнение и показали возможные расположения относительно начала координат.
Если вершина параболы смещена в точку 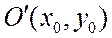
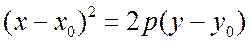
Выводом остальных кривых второго порядка мы заниматься не будем. Желающие могут найти все выкладки в рекомендуемой литературе.
Ограничимся их определениями и уравнениями.
7.6. Каноническое уравнение эллипса
Чтобы распечатать файл, скачайте его (в формате Word).
Уравнение прямой, проходящей через заданную точку перпендикулярно заданной прямой
В данной статье научимся составлять уравнения прямой, проходящей через заданную точку на плоскости перпендикулярно заданной прямой. Изучим теоретические сведения, приведем наглядные примеры, где необходимо записать такое уравнение.
Принцип составления уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой
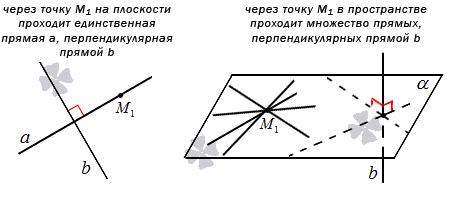
Перед нахождением уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой. Теорема рассматривается в средней школе. Через заданную точку, лежащую на плоскости, можно провести единственную прямую, перпендикулярную данной. Если имеется трехмерное пространство, то количество таких прямых увеличится до бесконечности.
Отсюда можно прийти к выводу, что составление уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой применимо только для случая на плоскости.
Задачи с трехмерным пространством подразумевают поиск уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.
Полученное уравнение прямой, проходящее через заданную точку плоскости перпендикулярно заданной. Если того требуют обстоятельства, можно переходить к другому виду данного уравнения.
Решение примеров
Рассмотрим составление уравнения прямой, проходящей через заданную точку плоскости и перпендикулярно заданной прямой.
Полученное уравнение является искомым.
Перпендикулярные прямая и плоскость, признак и условия перпендикулярности прямой и плоскости
Статья раскрывает понятие о перпендикулярности прямой и плоскости, дается определение прямой, плоскости, графически иллюстрировано и показано обозначение перпендикулярных прямой и плоскости. Сформулируем признак перпендикулярности прямой с плоскостью. Рассмотрим условия, при которых прямая и плоскость будут перпендикулярны с заданными уравнениями в плоскости и трехмерном пространстве. Все будет показано на примерах.
Перпендикулярные прямая и плоскость – основные сведения
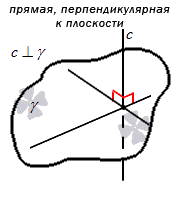
Прямая перпендикулярна к плоскости, когда она перпендикулярна к любой прямой, лежащей в этой плоскости.
Верно то, что и плоскость перпендикулярна к прямой, как и прямая к плоскости.
Например, если прямая перпендикулярна к плоскости, тогда возможно провести только одну прямую, благодаря которой две смежных стены комнаты пересекутся. Прямая считается перпендикулярной к плоскости потолка. Канат, расположенный в спортзале рассматривается в качестве отрезка прямой, который перпендикулярен плоскости, в данном случае полу.
При наличии перпендикулярной прямой к плоскости, угол между прямой и плоскостью считается прямым, то есть равен 90 градусов.
Перпендикулярность прямой и плоскости – признак и условия перпендикулярности
Для нахождения выявления перпендикулярности необходимо использовать достаточное условие перпендикулярности прямой и плоскости. Оно гарантирует выполнение перпендикулярности прямой и плоскости. Данное условие считается достаточным и называют признаком перпендикулярности прямой и плоскости.
Для перпендикулярности заданных прямой и плоскости достаточно, чтобы прямая была перпендикулярна двум пересекающимся прямым, которые лежат в этой плоскости.
При условии параллельности хоть одной из прямых плоскости, считается, что вторая прямая также перпендикулярна к данной плоскости.
Признак перпендикулярности прямой и плоскости рассматривается еще со школы, когда необходимо решить задачи по геометрии. Рассмотрим подробнее еще одно необходимое и достаточное условие, при котором прямая и плоскость будут перпендикулярны.
Данное доказательство основывается на необходимом и достаточном условии перпендикулярности прямой и плоскости, направляющего вектора прямой и нормального вектора плоскости.
Данное условие применимо для доказательства перпендикулярности прямой и плоскости, так как достаточно найти координаты направляющего вектора прямой и координаты нормального вектора в трехмерном пространстве, после чего производить вычисления. Используется для случаев, когда прямая определена уравнением прямой в пространстве, а плоскость уравнением плоскости некоторого вида.
Необходимо произвести проверку выполнимости условия. Получаем, что
Ответ: прямая и плоскость перпендикулярны.
Чтобы ответить на вопрос перпендикулярности, необходимо, чтобы было выполнено необходимое и достаточное условие, то есть для начала нужно найти вектор заданной прямой и нормальный вектор плоскости.
Ответ: прямая и плоскость не перпендикулярны.
График линейной функции, его свойства и формулы
Понятие функции
Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Понятие линейной функции
Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Для удобства результаты можно оформлять в виде таблицы:
Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».
| Функция | Коэффициент «k» | Коэффициент «b» |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».
Свойства линейной функции
Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1 /3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.
В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).
В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.
Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).
Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.
При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.
Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.
Если k 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Точки пересечения графика функции y = kx + b с осями координат:
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).