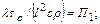при степени искажения в случае приближенного моделирования характерный параметр модели равен

Анализ размерностей

Основные понятия теории моделирования

Моделированием называется метод экспериментального изучения модели явления вместо натурного явления. Модель выбирают так, чтобы результаты эксперимента можно было распространить на натурное явление.

Пусть моделируется поле величины w. Тогда при точном моделировании в сходственных точках модели и натурного объекта должно соблюдаться условие

(9.1)

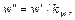
где 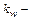масштаб моделирования.

В случае приближенного моделирования получим

(9.2)

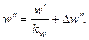
Отношение 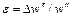называется степенью искажения.

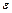
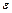
Если степень искажения не превосходит точности измерения, то приближенное моделирование не отличается от точного. Нельзя заранее сделать так, чтобы величина не превышала некоторого наперед заданного значения, так как в большинстве случаев ее нельзя заранее даже определить.

Метод аналогий

Если два физических явления различной физической природы описываются тождественными уравнениями и условиями однозначности (краевыми или в стационарном случае граничными условиями), представленными в безразмерной форме, то явления называются аналогичными. При этих же условиях явления одной физической природы называются подобными.

(9.3)

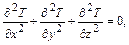
где 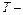абсолютная температура,

и уравнение электрического потенциала

(9.4)

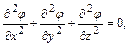
где 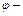электрический потенциал, аналогичны. В безразмерной форме эти уравнения будут тождественны.

Если созданы граничные условия для потенциала, аналогичные условиям для температуры, то в безразмерной форме они будут также тождественны.

Электротепловая аналогия широко используется при изучении процессов теплопроводности. Например, температурные поля лопаток газовых турбинин были измерены этим методом.

Анализ размерностей

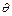
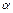
Все физические величины можно разделить на первичные и вторичные. Для процессов теплообмена за первичные обычно выбирают следующие: длину L, массу m, время t, количество теплоты Q избыточную температуру . Тогда вторичными будут такие величины, как коэффициент теплоотдачи температуропроводность a и т. п.

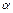
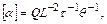
Формулы размерности вторичных величин имеют вид степенных одночленов. Например, формула размерности для коэффициента теплоотдачи имеет вид

(9.5)

где Q –количество теплоты.

Пусть известны все физические величины, существенные для изучаемого процесса. Требуется найти безразмерные комплексы.

Составим произведение из формул размерностей всех существенных для процесса физических величин в некоторых неопределенных пока степенях; очевидно, оно будет степенным одночленом (для процесса). Предположим, что его размерность (степенного одночлена) равна нулю, т. е. показатели степеней первичных величин, входящих в формулу размерностей, сократились, тогда степенной одночлен (для процесса) можно представить в форме произведения безразмерных комплексов из размерных величин. Значит, если составить произведение из формул размерностей, существенных для процессов физических величин в неопределенных степенях, то из условия равенства нулю суммы показателей степеней первичных величин этого степенного одночлена можно определить искомые безразмерные комплексы.

Покажем эту операцию на примере периодического процесса теплопроводности в твердом теле, омываемом жидким теплоносителем. Будем считать, что дифференциальные уравнения для рассматриваемого процесса неизвестны. Требуется найти безразмерные комплексы.

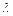
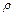
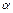
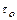
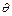
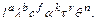
Существенными физическими величинами для изучаемого процесса будут следующие: характерный размер l (м), теплопроводность твердого тела , (Дж/(м К)), удельная теплоемкость твердого тела с (Дж/(кг К)), плотность твердого тела (кг/м 3 ), коэффициент теплообмена (теплоотдачи) (Дж/м 2 К)), время периода , (с), характерная избыточная температура (К). Составим из этих величин степенной одночлен вида

(9.6)

Показатель степени при первичной величине называется раз мерностью вторичной величины по отношению к данной первичной.

Заменим в физические величины (кроме Q) их формулами размерности, в результате получим

(9.7)

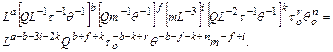
В данном случае показатели степени 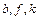имеют значения, при которых Q выпадает из уравнения.

Приравняем нулю показатели степеней одночлена:

для количества теплоты Q

0; (9.9)

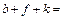
для времени

= 0; (9.10)

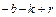
для температуры

0; (9.11)

0. (9.12)

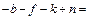
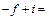
Всего существенных величин семь, уравнений для определения показателей пять, значит, только два показателя, например, b и kмогут быть выбраны произвольно.

Выразим все показатели степеней через b и k. В результате получим:

(9.13)

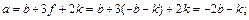
n = b + f + k = b + (-b – k) + k = 0; (9.16)

Теперь одночлен можно представить в форме

(9.18)

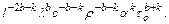
Так как показатели b и k могут быть выбраны произвольно, положим:

1. при этом запишем

(9.19)

(9.20)

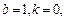
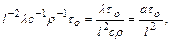
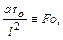
обозначим

2. b = 0, k = 1, при этом запишем

(9.21)

(9.22)

(9.23)

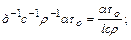
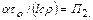
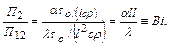
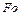
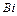
Итак, методом анализа размерностей найдены безразмерные комплексы. В рассматриваемом случае ими оказались числа подобия Фурье и Био ю

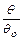
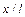
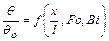
Введем безразмерные – искомую переменную и независимую переменную (одномерный случай). Тогда искомую обобщенную зависимость можно представить в форме

. (9.24)

Правильность полученного результата подтверждает так называемая 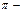теорема Бэкингема, которая формируется так: число безразмерных комплексов равно числу физических величин, существенных для процесса, минус число первичных величин.

Дата добавления: 2016-02-16 ; просмотров: 1877 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Моделирование при геометрическом искажении модели

Моделирование водных потоков значительных геометричес­ких размеров с малой шероховатостью русла представляет значительные трудности даже при наличии автомодельно-сти. Это сопряжено главным образом с невозможностью выполнить условие из-за чрезвычайно ма­лой высоты выступов шероховатости Δ_м на модели (несмот­ря даже на использование материалов с гладкой поверх­ностью, лакировкой поверхности и других приемов), т. е. когда размеры и оборудование лаборатории не позволяют изготовить и разместить модель необходимого геометричес­кого масштаба. Получить удовлетворительные результаты можно, назначая разные геометрические масштабы верти­кальных m_h и горизонтальных т_l размеров модели, причем m_h λ_Н (для широких русл m_λ= m_h/ т_l;

2) масштаб уклонов дна, очевидно, равен m_i= m_h/ т_l;

3) масштаб скорости ;

5) условие Fr_M=Fr_H при этом удовлетворяется;

6) если масштабы ширины и глубины совпадают, т. е.
т_b=т_h, а искажается только продольный масштаб т_l то масштаб расхода m_Q=m_h 5/2 ;

7) соотношение масштабов ширины и глубины потоков обычно принимают равным т_b/т_h= 2-5, хотя иногда это соотношение доводят до m_b/m_h=10;

8) геометрическое искажение модели при m_h

Обоснование описываемого метода затрагивает широкий круг вопросов, в частности: обоснование самой возможности замены натурного без­напорного водного потока воздушным напорным потоком на модели; обоснование возможности замены свободной поверхности жесткой стенкой, что нарушает граничные условия; обоснование возможности геометрического искажения модели и т. д.

Дополнительные трудности связаны с тем, что свобод­ная поверхность натурного потока часто является неизвестной, а ее конфигурация является целью поиска.

Искажения, вносимые жесткой стенкой (обычно стеклом), сводятся к следующему:

на жесткой стенке, имитирующей свободную поверх­ность, развиваются силы трения, которыми в натуре можно пренебречь;

форму свободной поверхности на модели часто прини­мают плоской, что заведомо не соответствует свободной по­верхности в натуре;

Таким образом, воздушно-напорная модель потока яв­ляется искаженной в любом случае и при ее использовании можно рассчитывать на достижение лишь приближенного подобия потоков.

Если форма свободной поверхности натурного потока известна заранее, при воспроизведении ее жесткой стенкой на воздушно-напорной модели можно рассчитывать на получение хороших результатов.

Лучших результатов при воздушно-напорном модели­ровании достигают в тех случаях, когда деформации сво­бодной поверхности натурных потоков незначительны и их можно считать «плановыми». Для воздушно-напорной модели следует принимать Re_M>20 000, а глубину (толщину) напорного потока не назначать менее 4 мм. Кроме того, чтобы сохранить автомодельность воздушного (сжимаемого) потока к критерию Маха, необходимо соблюдать условие u_м≤60 м/с.

Источник

Приближённое моделирование

Приближённое моделирование — составление ограниченных выборок и обобщение выводов об этой выборке на более широкую популяцию. Например, при участии в исследовании студентов 2-го курса университета, данные этого исследования распространяются на «людей в возрасте от 17 до 21 года». Допустимость подобных обобщений крайне ограничена.

Приближенное моделирование – формирование модели, которая для четко оговоренного класса систем (процессов) описывает его поведение (или нужные явления) с приемлемой точностью.

10. Основные этапы психологического (научного и практического) исследования.

Психологическое исследование: этапы,изучение состояния проблемы, литературный обзор. Учитывая общность теоретического и эмпирического исследования, рассмотрим схему этапов, которые обычно включает психологическое исследование.
Основные этапы психологического исследования. Наиболее часто психологическое исследование включает следующие шаги:
1. Изучение состояния проблемы. Постановка проблемы, выбор объекта и предмета исследования. Обзор имеющихся по данной проблеме публикаций.

2. Разработка или уточнение исходной исследовательской концепции. Построение в общих чертах модели интересующего явления. Выдвижение гипотез.

3. Планирование исследования. Определение целей и задач. Выбор методов и методик.

4. Сбор данных и фактуальное описание. В теоретическом исследовании: поиск и отбор фактов, их систематизация, фактуальное описание под новым углом зрения.

5. Обработка данных (эмпирического материала исследования).

6. Оценивание результатов проверки гипотез, интерпретация результатов в рамках исходной исследовательской концепции.
7. Соотнесение результатов с существующими концепциями и теориями. Уточнение модели изучаемого явления. Формулирование общих выводов. Последовательное прохождение по перечисленным этапам весьма условно в реальном исследовании, поскольку практически всегда возникает необходимость корректировать решения более ранних этапов с учетом возможностей и ограничений последующих.
Прикладная психология – общий термин, используемый для обозначения всех тех отраслей психологии, которые стремятся применить принципы, открытия и теории психологии на практике в различных областях.
Направления исследования – теоретическое, эмпирическое, прикладное – не являются взаимоисключающими. Более того, их сочетание (не всегда возможное) позволяет прийти к более надежным выводам, способствует их принятию в более широких кругах ученых и практиков.

При изучении состояния проблемы целесообразна следующая последовательность работы:
1. Ознакомиться с определениями основных понятий, относящихся к рассматриваемой теме, используя словари и энциклопедии. В них часто можно найти ссылки на наиболее известные работы в данной области и на ученых, внесших основной склад в исследование изучаемого явления.

2. Составить библиографию по интересующей вас теме с помощью систематического каталога. В систематическом каталоге библиографические ссылки сгруппированы по темам.

3. Осуществить предварительное знакомство с предметом исследования.

4. Ознакомиться со справочными и библиографическими изданиями по психологии, общественным наукам.
Проделав библиографическую подготовку, вы будете иметь представление о количестве публикаций по интересующей вас теме, о временных рамках публикаций, об интересе ученых к данной проблеме, сможете выделить наиболее плодовитых авторов.
В конспекте работы, описывающей экспериментальное исследование, надо отметить его характеристики:
• перечень использованных методик, • описание оригинальных (авторских) методик, • описание процедуры эксперимента, объем выборки испытуемых, • социально-демографические и другие значимые параметры выборки (всегда важны данные о возрасте, поле, уровне образования, профессии, принадлежности к определенной социальной группе, здоровье, психических или соматических расстройствах). В литературном обзоре обязательно должны быть названы фамилии авторов, идеи или экспериментальные результаты которых вы пересказываете или обобщаете. Ссылаться следует, указывая конкретные публикации авторов.

11. Характеристика основных методов психодиагностического исследования.

Характеристика методов психологического исследования:

Методы научных исследований – это те приемы и средства, с помощью которых ученые получают достоверные сведения, используемые далее для построения научных теорий и выработки практических рекомендаций.

Наряду с математизацией и технизацией исследований в психологии до сих пор не утратили своего значения традиционные методы сбора научной информации, в том числе такие, как наблюдение, самонаблюдение и опрос.

Основные методы психологических исследований и их варианты, применяемые для сбора первичных данных.

Наблюдениеимеет несколько вариантов.

Внешнее наблюдение – это способ сбора данных о психологии и поведении человека путем прямого наблюдения за ним со стороны. Внешнее наблюдение менее субъективно, чем самонаблюдение, и обычно применяется там, где признаки, за которыми необходимо наблюдать, легко могут быть выделены и оценены извне.

Внутреннее наблюдение, или самонаблюдение, применяется тогда, когда психолог-исследователь ставит перед собой задачу изучить интересующее его явление в том виде, в каком оно непосредственно представлено в его сознании. Внутренне воспринимая соответствующее явление, психолог как бы наблюдает за ним (например, за своими образами, чувствами, мыслями, переживаниями). Свободное наблюдение не имеет заранее установленных рамок, программы, процедуры его проведения. Оно может менять предмет или объект наблюдения, его характер в ходе самого наблюдения в зависимости от пожелания наблюдателя. Свободное наблюдение целесообразно проводить в тех случаях, когда невозможно точно определить, что следует наблюдать, когда признаки изучаемого явления и его вероятный ход заранее не известны исследователю.

Стандартизированное наблюдение, напротив, заранее определено и четко ограничено в плане того, что наблюдается. Оно ведется по определенной, предварительно продуманной программе и строго следует ей, независимо от того, что происходит в процессе наблюдения с объектом или самим наблюдателем. Стандартизированное наблюдение лучше использовать тогда, когда у исследователя имеется точный и достаточно полный перечень признаков, относимых к изучаемому феномену.

При включенном наблюдении (оно чаще всего используется в общей, возрастной, педагогической и социальной психологии) исследователь выступает в качестве непосредственного участника того процесса, за ходом которого он ведет наблюдение. Например, психолог может решать в уме какую-либо задачу, одновременно наблюдая за собой. Другой вариант включенного наблюдения: исследуя взаимоотношения людей, экспериментатор может включиться сам в общение с наблюдаемыми людьми, не прекращая в то же время наблюдать за складывающимися между ними и этими людьми взаимоотношениями. Включенное наблюдение полезно в том случае, когда психолог может дать правильную оценку явлению, лишь прочувствовав его на самом себе. Однако если под влиянием личного участия исследователя его восприятие и понимание события может быть искажено, то лучше обращаться к стороннему наблюдению, применение которого позволяет более объективно судить о наблюдаемом. Стороннее наблюдение в отличие от включенного не предполагает личного участия наблюдателя в том процессе, который он изучает.

Письменный опрос позволяет охватить большее количество людей. Наиболее распространенная его форма – анкета. Но ее недостатком является то, что, применяя анкету, нельзя заранее учесть реакции отвечающего на содержание ее вопросов и, исходя из этого, изменить их.

Свободный опрос – разновидность устного или письменного опроса, при которой перечень задаваемых вопросов и возможных ответов на них заранее не ограничен определенными рамками. Опрос данного типа позволяет достаточно гибко менять тактику исследования, содержание задаваемых вопросов, получать на них нестандартные ответы. В свою очередь стандартизированный опрос, при котором вопросы и характер возможных ответов на них определены заранее и обычно ограничены достаточно узкими рамками, более экономичен во времени и в материальных затратах, чем свободный опрос.

Тестыявляются специализированными методами психодиагностического обследования, применяя которые можно получить точную количественную или качественную характеристику изучаемого явления. От других методов исследования тесты отличаются тем, что предполагают четкую процедуру сбора и обработки первичных данных, а также своеобразие их последующей интерпретации. С помощью тестов можно изучать и сравнивать между собой психологию разных людей, давать дифференцированные и сопоставимые оценки.

Специфика эксперимента как метода психологического исследования заключается в том, что в нем целенаправленно и продуманно создается искусственная ситуация, в которой изучаемое свойство выделяется, проявляется и оценивается лучше всего. Основное достоинство эксперимента состоит в том, что он позволяет надежнее, чем все остальные методы, делать выводы о причинно-следственных связях исследуемого явления с другими феноменами, научно объяснять происхождение явления и развитие. Однако организовать и провести настоящий, отвечающий всем требованиям психологический эксперимент на практике бывает нелегко, поэтому в научных исследованиях он встречается реже, чем другие методы.

Имеются две основные разновидности эксперимента: естественный и лабораторный. Друг от друга они отличаются тем, что позволяют изучать психологию и поведение людей в условиях, отдаленных или приближенных к действительности. Естественный эксперимент организуется и проводится в обычных жизненных условиях, где экспериментатор практически не вмешивается в ход происходящих событий, фиксируя их в том виде, как они разворачиваются сами по себе. Лабораторный эксперимент предполагает создание некоторой искусственной ситуации, в которой изучаемое свойство можно лучше всего изучить. Данные, получаемые в естественном эксперименте, лучше всего соответствуют типичному жизненному поведению индивида, реальной психологии людей, но не всегда точны из-за отсутствия у экспериментатора возможности строго контролировать влияние всевозможных факторов на изучаемое свойство. Результаты лабораторного эксперимента, напротив, выигрывают в точности, но зато уступают в степени естественности – соответствия жизни.

Модели могут быть техническими, логическими, математическими, кибернетическими.Математическаямодель представляет собой выражение или формулу, включающую переменные и отношения между ними, воспроизводящие элементы и отношения в изучаемом явлении. Техническое моделирование предполагает создание прибора, по своему действию напоминающего то, что подлежит изучению. Кибернетическое моделирование основано на использовании в качестве элементов модели понятий из области информатики и кибернетики. Логическое моделирование основано на идеях и символике, применяемой в математической логике. Логическое моделированиешироко используется при изучении мышления человека и его сравнении с решением задач вычислительной машиной. Примеры технического моделирования встречаются в научных исследованиях, посвященных изучению восприятия и памяти человека. Это попытки построения спец.машин, способных наподобие человека воспринимать и перерабатывать сенсорную информацию, запоминать и воспроизводить ее.

Источник