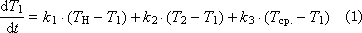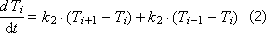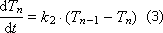примеры математических моделей с распределенными параметрами
Модели с сосредоточенными и распределенными параметрами
Модели бывают статистическими и логико-математическими, основанными на уравнениях, с той или иной степенью точности описывающих влияние разных факторов на изучаемый объект, явление или процесс. Логико-математические модели делятся на три класса: 1) модели с сосредоточенными параметрами; 2) модели с сосредоточенно-распределенными параметрами, т. е. переходные; 3) модели с распределенными параметрами, основанные на дифференциальных уравнениях в частных производных.
Математическая модель с сосредоточенными параметрами— это модель системы, поведение которой описывается обыкновенными дифференциальными уравнениями.
Данная модель включает в себя переменные, которые зависят только от времени и не зависят от координат. Математическая модель с сосредоточенными параметрами имеет вид системы обыкновенных дифференциальных уравнений.
Решением дифференциального уравненияназывается n раз дифференцируемая функция x(t), удовлетворяющая уравнению во всех точках своей области
определения. Обычно существует целое множество таких функций, и для выбора одного из них требуется наложить на него дополнительные условие, например: потребовать, чтобы решение принимало в данной точке данное значение.
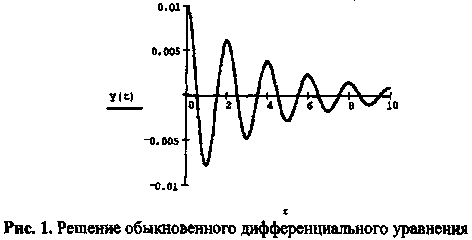
Пример. Дифференциальное уравнение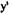 
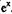
= у (вместе с начальным условием у(0) =1) задает экспоненту: у(х) = 
. Если х обозначает время, то эта функция описывает рост популяции в условиях неограниченности ресурсов.
Математическая модель с распределенными параметрами— модель системы, описываемая дифференциальными уравнениями в частных производных.
Модель содержит переменные, зависящие от пространственных координат, и представляет собой систему дифференциальных уравнений в частных производных или систему интегро-дифференциальных уравнений. Важной характеристикой дифференциальных уравнений является их порядок, т. е. порядок старшей производной, которая входит в эти уравнения.
Пример. Уравнение колебания струны. Данное уравнение имеет вид:
Лекция 17.
Моделирование систем
с распределенными параметрами
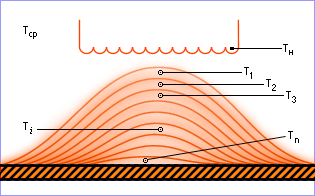
Если объект характеризуется некоторым параметром, различным по своему значению в разных точках объекта, то можно сказать, что значения такого параметра распределены (по объекту). Если таких параметров несколько, то объект рассматривается как система с распределенными параметрами. Для осуществления расчетов систему в таком случае удобно разбить на элементарные объемы (слои). Покажем это на примере.
| |
| Рис. 17.1. Схема технологического процесса сушки материала, разбитого на слои |
Изменение температуры в первом слое ( Tн температура нагревателя, Tср температура среды):
Тогда поведение системы «кучи сырья» опишется системой дифференциальных уравнений, каждое из которых опишет отдельный слой «кучи».
| |
| Рис. 17.2. Блок-схема моделирования распределенной системы (на примере процесса сушки) |
Опять следует обратить внимание на то, что цикл расчета производных и цикл расчета нового состояния системы отделены друг от друга во избежание появления «эффекта гонок».
Итак, инструментом моделирования распределенных систем являются вложенные циклы, по крайней мере, двойные внутри цикла «по времени» содержится цикл «по пространству».
Модель может выглядеть по-разному в зависимости от платформы, на которой она реализуется. Выше (см. рис. 17.2 ) был разобран пример, показывающий алгоритмический способ описания расчета поведения распределенной системы, использующий язык и архитектуру фон неймановской машины (см. рис. 17.3 ).
| |
| Рис. 17.3. Фон неймановская архитектура вычислительной системы (с общей шиной, звезда) |
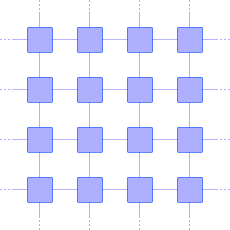
Представьте, что мы используем для моделирования структуру не фон неймановской машины (см. лекцию 02 ИИ), которая состоит из МНОЖЕСТВА элементарных одинаковых вычислительных элементов, соединенных между собой в сеть (см. рис. 17.4 ). При такой архитектуре элементы существуют одновременно, то есть параллельно синхронно во времени и в конце каждого такта обмениваются выходными (входными) сигналами между собой, соседями по сети. Такая парадигма вычислительной платформы имитирует более адекватно окружающий нас мир.
| |
| Рис. 17.4. Не фон неймановская архитектура вычислительной системы (однородная, параллельная сеть вычислительных элементов) |
Используя машину фон Неймана, архитектуру с общей шиной (звезду), мы тем самым организуем процесс вычислений алгоритмически, представляя его как последовательность шагов. Сам алгоритм выполняется на одном и том же ресурсе единственном процессоре, который через шину (центральный узел звезды) запрашивает шаг за шагом память по поводу состояния каждого из рассчитываемых им элементов. Центральный узел (шина), таким образом, является узким местом. Процессор обрабатывает такт за тактом каждый элемент имитируемой системы, которые выстраиваются в очередь к нему на обработку.
В окружающем нас мире, который мы пытаемся имитировать, в действительности сущности автономны, живут как бы сами по себе параллельно во времени, проявляя свои свойства посредством взаимодействия с соседями по пространству.
Поставим во взаимно однозначное соответствие элементарные сущности имитируемого сложного объекта из реального мира элементарным вычислителям каждый вычислительный элемент будет имитировать одну определенную сущность (см. рис. 17.5, а ). Для этого в вычислительном элементе запишем закон функционирования именно той сущности, которую он будет имитировать (см. рис. 17.5, б ).
| |
| Рис. 17.5. Иллюстрация принципа объектного отражения мира в информационных моделях |
Для нашей задачи расчета теплопроводности запись закона изменения температуры для элементарного объема будет иметь следующий вид:
Каждый элемент вычислительной сети производит одну и ту же, причем, единственную, операцию, реализует одну и ту же модель, причем, элементарную. Это особенность параллельных структур.
Далее свяжем вычислительные элементы связями так же, как контактируют между собой элементы реального мира.
Итак, есть две принципиально разные вычислительные архитектуры фон неймановская и не фон неймановская (обе предложены фон Нейманом):
Запустите последовательно три проекта: «Дом-1», «Дом-2» и «Дом-3».
Обратите внимание, в первом случае мы рассматриваем комнату как одно целое. Дом представляет собой сосредоточенную систему из двух элементов, на которые действует окружающая среда 
и дополнительные (внешние) источники нагрева (батареи) 
. В данном случае разработчик проекта предполагает температуру в разных местах одной комнаты единой.
В модели 2 проектировщик усложнил проект, установив в него дополнительные компоненты интерфейса для удобства использования. Мы видим процесс формализации в развитии. На модель накладывается интерфейс, важным здесь является то, что он в данной нотации отделен от модели. Мы можем легко заменять отдельные элементы интерфейса независимо друг от друга.
Если мы хотим уточнить модель, считая, что температуры в разных углах комнаты могут быть разными, что в действительности именно так, то нам придется разбить комнаты на более мелкие элементы, организовать их описание и установить между ними связи. Имитация станет более точной, поэтому в модели 3 вы можете уже исследовать более тонкие эффекты попробуйте открывать и закрывать окна и двери, менять температуры отопительных приборов и окружающей среды и посмотрите на результат (см. рис. 17.6 ).
| |
| Рис. 17.6. Результат работы модели распределенной системы при различных условиях и внешних воздействиях |
Примечание. Справедливости ради, следует отметить, что, несмотря на то, что вы видите элементы вычислительной сети, имитируете вы в конечном итоге на последовательной машине (машине процессов, алгоритмической машине) за неимением в настоящий момент у вас не фон неймановской машины. Компенсирует (маскирует) сложности алгоритмического способа мышления среда моделирования Stratum-2000, которая имитирует работу параллельной объектно-ориентированной машины на фон неймановской структуре. Но при наличии у вас не фон неймановской машины вы бы без каких-либо изменений перенесли бы в автоматическом режиме проект на сеть вычислителей. Такой перенос принято называть отражением объекта в имитационную среду.
То есть в проекте 3 мы фактически видим параллельную объектно-ориентированную систему. Структура не фон неймановской машины поддерживает объектно-ориентированный способ моделирования (см. лекцию 32).
Распределенность и сосредоточенность параметров
В пространственно протяженных объектах, в частности включающих в себя непрерывные среды (газы, жидкости, твердые среды), когда время распространения физических, например колебательных явлений, оказывается соизмеримым с инерционными эффектами, адекватное описание процессов требует учета как временных, так и пространственных координат. Объекты такого рода, средством описания которых служат дифференциальные уравнения в частных производных, относятся к классу объектов с распределенными параметрами. С математической точки зрения объекты с распределенными параметрами представляют собой поле, существующее в пространственно-временном континууме, а переменные соответствующих моделей в общем случае суть функции времени и пространственных координат. Типичными примерами одномерных объектов с распределенными параметрами служат всевозможные «длинные линии»: проводные линии связи, длинные трубопроводы, линии электропередачи на большие расстояния. Примерами моделей двухмерного объекта с распределенными параметрами являются сечения различных трубопроводов, кабелей, проводов, где рассматриваются в плоскостях поля температур, плотностей и напряженностей. И, наконец, пространственное электромагнитное поле с его математической моделью – уравнениями Максвелла – представляет собой классический пример трехмерного объекта с распределенными параметрами.
Если пространственной протяженностью можно пренебречь и считать, что независимой переменной протекающих в нем процессов является только время, принято говорить об объекте с сосредоточенными параметрами. К числу таких объектов, которые описываются обыкновенными дифференциальными уравнениями, относится подавляющее большинство механизмов, машин, устройств, а также все системы, у которых расстояния между отдельными элементами практически не влияют на исследуемые свойства.
Математический аппарат, строго описывающий объекты с распределенными параметрами, существенно сложнее, чем аппарат объекта с сосредоточенными параметрами. Поэтому на практике всегда, где это возможно, прибегают к аппроксимации, т. е. заменяют распределенные параметры на сосредоточенные, например, разбивая пространство на небольшие элементы (подпространства) или делая корректировку сосредоточенных параметров.
Дата добавления: 2015-03-19 ; просмотров: 1088 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
14. Понятие динамической системы
Динамическими системами называют класс задач, представленных задачами Коши для обыкновенных дифференциальных уравнений (ОДУ) или систем таких уравнений.
Теория динамических систем и специфические численные методы наиболее развиты для динамических систем, описываемых ОДУ (более простые уравнения).
Задача Коши для системы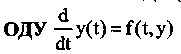
состоит в отыскании неиз-
вестной векторной функции y(t), включающей несколько (L) неизвестных функций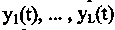
, для начального условия у(0) = С.
Соответственно числу компонент векторной функции y(t) должно быть поставлено L начальных условий. Исходя из физического смысла такой постановки задачи можно, не теряя общности, полагать, что дифференциальные уравнения содержат производные по аргументу t, являющемуся временем, и, соответственно, описывают динамику во времени различных физических параметров y(t). Поэтому задачи Коши для таких моделей называют динамическими системами, а для их изучения центральным моментом является анализ фазовых портретов, т. е. решений, получающихся при выборе всевозможных начальных условий.
Решения обыкновенных дифференциальных уравнений часто удобнее изображать не в привычном виде
, а в фазовом пространстве, по осям которого откладываются значения каждой из найденных функций. При этом аргументtвходит в графики лишь параметрически (см. рис. 1).
Классические примеры моделей динамических систем, описываемых системами ОДУ: нелинейный осциллятор, динамика популяций (Вольтерра), электронный генератор автоколебаний (Ван дер Поля), турбулентная конвекция жидкости (Лоренца), химическая реакция с диффузией (Пригожина). Все примеры являются типичными динамическими системами и содержат производные по времени t, описывая динамику различных физических параметров.
15. Модели с сосредоточенными и распределенными параметрами
Модели бывают статистическими и логико-математическими, основанными на уравнениях, с той или иной степенью точности описывающих влияние разных факторов на изучаемый объект, явление или процесс. Логико-математические модели делятся на три класса: 1) модели с сосредоточенными параметрами; 2) модели с сосредоточенно-распределенными параметрами, т. е. переходные; 3) модели с распределенными параметрами, основанные на дифференциальных уравнениях в частных производных.
Данная модель включает в себя переменные, которые зависят только от времени и не зависят от координат. Математическая модель с сосредоточенными параметрами имеет вид системы обыкновенных дифференциальных уравнений.
Решением дифференциального уравнения называется n раз дифференцируемая функция x(t), удовлетворяющая уравнению во всех точках своей области
определения. Обычно существует целое множество таких функций, и для выбора одного из них требуется наложить на него дополнительные условие, например: потребовать, чтобы решение принимало в данной точке данное значение.
Пример. Дифференциальное уравнение
= у (вместе с начальным условиему(0) =1) задает экспоненту: у(х) =
. Если х обозначает время, то эта функцияописывает рост популяции в условиях неограниченности ресурсов.
Модель содержит переменные, зависящие от пространственных координат, и представляет собой систему дифференциальных уравнений в частных производных или систему интегро-дифференциальных уравнений. Важной характеристикой дифференциальных уравнений является их порядок, т. е. порядок старшей производной, которая входит в эти уравнения.
Пример. Уравнение колебания струны. Данное уравнение имеет вид:
Математические модели с сосредоточенными параметрами.
Математические модели с распределенными параметрами.
Моделями этого типа описываются процессы диффузии, теплопроводности, распространения волн различной природы и т. п. Эти процессы могут быть не только физической природы. Математические модели с распределенными параметрами широко распространены в биологии, физиологии и других науках. Чаще всего в качестве основы математической модели применяют уравнения математической физики, в том числе и нелинейные.
Математические модели, основанные на экстремальных принципах.
Общеизвестна основополагающая роль принципа наибольшего действия в физике. Например, все известные системы уравнений, описывающие физические процессы, могут быть выведены из экстремальных принципов. Однако и в других науках экстремальные принципы играют существенную роль.
Основной принцип классификации математических моделей
В качестве основного принципа классификации математических моделей часто используют области их применения. При таком подходе выделяются следующие области применения:
технические приложения, в том числе управляемые системы, искусственный интеллект;
жизненные процессы (биология, физиология, медицина);
большие системы, связанные с взаимодействием людей (социальные, экономические, экологические);
гуманитарные науки (языкознание, искусство).
(Области применения указаны в порядке, соответствующем убыванию уровня адекватности моделей).
Виды математических моделей: детерминированные и вероятностные, теоретические и экспериментальные факторные. Линейные и нелинейные, динамические и статические. непрерывные и дискретные, функциональные и структурные.
По форме представления математических моделей различают инвариантную, алгоритмическую, аналитическую и графическую модели объекта проектирования.
Виды математических моделей технических объектов
По форме представления ММ
По характеру отображаемых свойств ТО
По степени абстрагирования
По способу получения ММ
(с распределенными параметрами)
ММ макроуровня (со средоточенными параметрами)
К математическим моделям предъявляются требования адекватности, экономичности, универсальности. Эти требования противоречивы.
По форме представления математических моделей различают инвариантную, алгоритмическую, аналитическую и графическую модели объекта проектирования.
В инвариантнойформе математическая модель представляется системой уравнений вне связи с методом решения этих уравнений.
Аналитическая модель представляет собой явные зависимости искомых переменных от заданных величин (обычно зависимости выходных параметров объекта от внутренних и внешних параметров). Такие модели получают на основе физических законов, либо в результате прямого интегрирования исходных дифференциальных уравнений. Аналитические математические модели позволяют легко и просто решать задачи определения оптимальных параметров. Поэтому, если представляется возможность получения модели в таком виде, ее всегда целесообразно реализовать, даже если при этом придется выполнить ряд вспомогательных процедур, Такие модели обычно получают методом планирования эксперимента (вычислительного или физического).
Графическая(схемная) модель представляется в виде графов, эквивалентных схем, динамических моделей, диаграмм и т.п. Для использования графических моделей должно существовать правило однозначного соответствия условных изображений элементов графической и компонентов инвариантной математических моделей.
Деление математических моделей на функциональные и структурные определяется характером отображаемых свойств технического объекта.
Структурныемодели отображают только структуру объектов и используются только при решении задач структурного синтеза. Параметрами структурных моделей являются признаки функциональных или конструктивных элементов, из которых состоит технический объект и по которым один вариант структуры объекта отличается от другого. Эти параметры называют морфологическими перемененными. Структурные модели имеют форму таблиц, матриц и графов. Наиболее перспективно применение древовидных графов типа И-ИЛИ-дерева. Такие модели широко используют на метауровне при выборе технического решения.