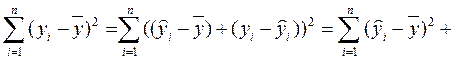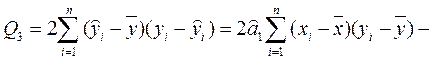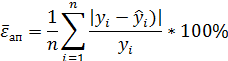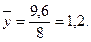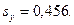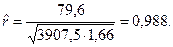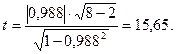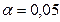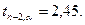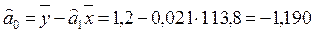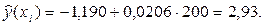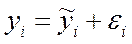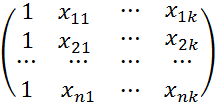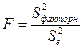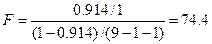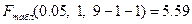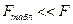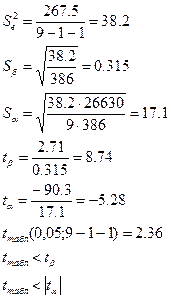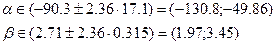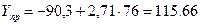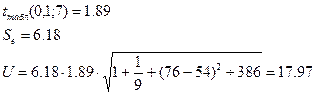проверка значимости параметров уравнения регрессии
Пример нахождения статистической значимости коэффициентов регрессии
Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии
Анализ точности определения оценок коэффициентов регрессии
S a = 0.2704
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 88,16
(128.06;163.97)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается
Fkp = 4.96
Поскольку F > Fkp, то коэффициент детерминации статистически значим.
Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению средней среднедневной заработной платы Y на 0.721 среднеквадратичного отклонения этого показателя.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:
2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя.
(a + bxp ± ε)
где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X p = 94
(76.98 + 0.92*94 ± 7.8288)
(155.67;171.33)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равно) на уровне значимости α=0.05.
tкрит = (10;0.05) = 1.812
Поскольку 3.2906 > 1.812, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=10, Fkp = 4.96
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).
Проверка значимости уравнения регрессии



Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
Проверка значимости уравнения регрессии производится на основе дисперсионного анализа.
В математической статистике дисперсионный анализ рассмотрен как самостоятельный метод статистического анализа. Здесь же он применяется как вспомогательное средство для изучения качества регрессионной модели.
Обозначим 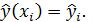
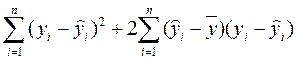
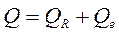
Убедимся в том, что пропущенное в (2.5.25) третье слагаемое 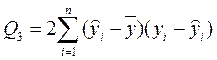
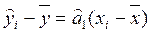
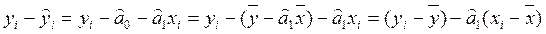
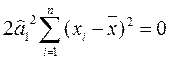
Схема дисперсионного анализа имеет вид, представленный в таблице.
| Компоненты дисперсии | Сумма квадратов | Число степеней свободы | Средние квадраты |
| Регрессия | 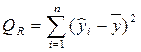 | m-1 | 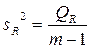 |
| Остаточная | 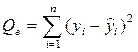 | n-m | 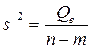 |
| Общая | 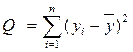 | n-1 |
Средние квадраты 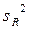
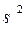
При отсутствии линейной зависимости между зависимой и объясняющими переменными случайные величины 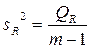
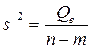
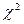
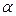
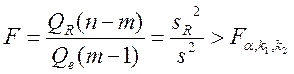
где 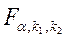
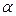
В случае линейной парной регрессии m=2, и уравнение регрессии значимо на уровне 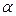
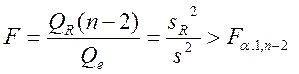
Мерой качества регрессионной модели, характеристикой прогностической силы регрессионной модели является коэффициент детерминации, определяемый по формуле
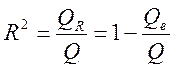
Величина R 2 показывает, какая часть (доля) вариации зависимой переменной обусловлена вариацией объясняющей переменной.
Так как 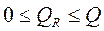
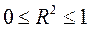
Чем ближе 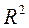
Средняя ошибка аппроксимации
Еще одним показателем качества построенной регрессионной зависимости является средняя ошибка аппроксимации, которая вычисляется по формуле
Эта величина представляет собой среднюю относительную ошибку.
Пример
Исследуем зависимость розничного товарооборота магазинов (млрд р.) от среднесписочного числа работников. Обозначим:
x – число работников;
Исходные данные и результаты расчетов приведены в таблице
| Номер магазина | 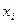 | 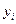 | 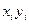 | 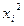 | 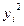 |
| 0,5 | 39,5 | 6 241 | 0,25 | ||
| 0,7 | 59,5 | 7 225 | 0,49 | ||
| 0,9 | 91,8 | 10 404 | 0,81 | ||
| 1,1 | 126,5 | 13 225 | 1,21 | ||
| 1,4 | 170,8 | 14 884 | 1,96 | ||
| 1,4 | 176,4 | 15 876 | 1,96 | ||
| 1,7 | 227,8 | 17 956 | 2,89 | ||
| 1,9 | 279,3 | 21 609 | 3,61 | ||
| Итого | 9,6 | 1171,6 | 107 420 | 13,18 |
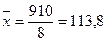
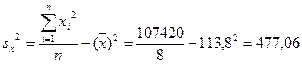
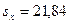
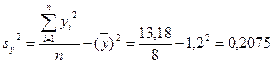
Вычислим выборочный коэффициент корреляции:
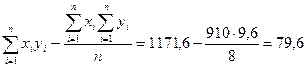
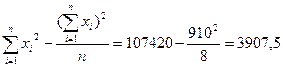
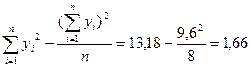
Проверим значимость выборочного коэффициента корреляции. Для этого вычислим статистику t:
Табличное значение критерия Стьюдента для 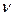
Найдем коэффициенты парной линейной регрессии:
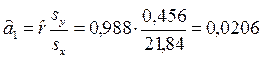
и регрессия имеет вид
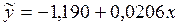
Прогнозное значение розничного товарооборота при 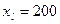
2.6. МНОЖЕСТВЕННАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ
Экономические явления, как правило, определяются большим числом одновременно и совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости одной зависимой переменной Y от нескольких объясняющих переменных X1, X2, …, Xk. Эта задача решается с помощью множественного регрессионного анализа.
Модель множественной линейной регрессии имеет вид
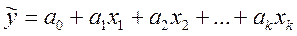
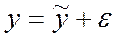
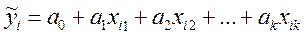
Модель (2.6.1), в которой зависимая переменная 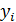
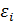
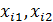
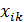
Включение в регрессионную модель новых объясняющих переменных усложняет получаемые формулы и вычисления. Это приводит к целесообразности использования матричных обозначений.
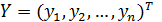
Х=
— матрица значений объясняющих переменных размера n(k+1).
где xij – значение j-ой переменной для i-го объекта выборки.
Обращаем внимание на то, что в матрицу Х дополнительно введен столбец, все элементы которого равны 1, т. е. условно полагается, что в модели (2.6.1) свободный член 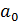
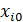
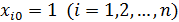
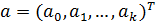
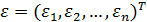
Тогда в матричном виде модель (2.6.1) примет вид
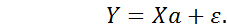
Как уже было отмечено, модель (2.6.2), удовлетворяющая приведенным предпосылкам 1-5, называется классической нормальной линейной моделью множественной регрессии. Если же среди приведенных предпосылок не выполняется лишь предпосылка 5 о нормальном законе распределения вектора возмущений ε, то модель (2.6.2) называется просто классической линейной моделью множественной регрессии.
Оценки параметров а0, a1, … ak можно получить с помощью рассмотренного ранее метода наименьших квадратов.
Система уравнений имеет вид
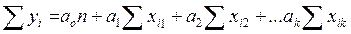
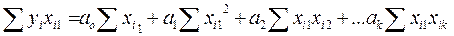
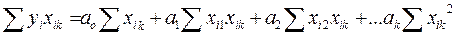
Суммирование производится по индексу i от 1 до n, где n –объем выборки.
Эту систему обычно записывают в матричном виде
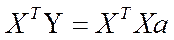
где 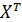
Умножив обе части уравнения слева на матрицу 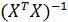
Проверка статистической значимости уравнения регрессии и его параметров
а) проверка статистической значимости уравнения:
Проверка значимости (существенности) уравнения регрессии позволяет установить, существенна ли связь включенных в уравнение признаков (Y и X), соответствует ли математическая модель, выражающая зависимость Y и X, фактическим данным и достаточно ли включенных в уравнение объясняющих переменных Х для описания зависимой переменной Y. Иными словами оценка значимости уравнения регрессии позволяет узнать пригодно ли оно для практического использования (например, для прогнозирования) или нет.
Оценка значимости уравнения регрессии проводится с помощью F-критерия Фишера:
или в терминах коэффициента детерминации
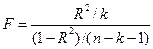
где n – длина совокупностей данных, k – количество факторов, включенных в модель (в уравнении парной регрессии k=1).
Уравнение регрессии статистически значимо, если
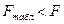
1) 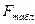
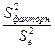
2) для определения 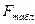
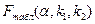


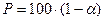
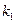
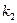
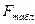
Пример (продолжение).
4) Проверить значимость уравнения регрессии с помощью F-критерия Фишера ( 
вывод: уравнение регрессии статистически значимо, связь включенных в него признаков существенна;
Значение F-критерия можно получить также в таблице «Дисперсионный анализ» отчета по работе с инструментом регрессия (рис. 13).
| Дисперсионный анализ | |||
| df | SS | MS | F |
| Регрессия | 2834.50 | 2834.50 | 74.2 |
| Остаток | 267.50 | 38.21 | |
| Итого | 3102.00 |
Рис. 13. Фрагмент регрессионного анализа
а) проверка статистической значимости параметров уравнения:
В линейной регрессии обычно оценивается значимость не только уравнения регрессии, но и отдельных его параметров. Для этого применяется t-критерий Стьюдента:
1) рассчитывают стандартные ошибки (среднеквадратические отклонения) 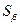
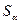
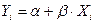
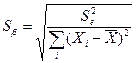
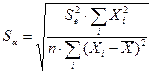
где 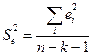
2) определяют расчетные значения t-критерия Стьюдента:
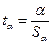
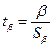
3) определяют табличное значение t-критерия 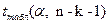

4) параметры уравнения регрессии будут статистически значимы, если выполняются неравенства:
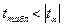
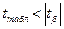
Замечания:
1) статистическая значимость (незначимость) коэффициента регрессии 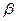
2) статистическая значимость (незначимость) параметра уравнения 
а) выбор вида уравнения;
б) определение независимых факторов для включения в модель;
3) t-критерий можно использовать также для определения интервальных оценок параметров модели:
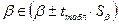
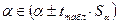
Поскольку коэффициент регрессии 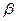
Пример (продолжение).
4) осуществить проверку значимости параметров уравнения регрессии по t-критерию Стьюдента ( 
Вывод: оба параметра модели статистически значимы.
Дополнение: интервальные оценки параметров
Расчетные значения t-критерия, а также интервальные оценки параметров можно найти в отчете по результатам работы с инструментом Регрессия (рис. 14).
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y | -90.33 | 17.12 | -5.28 | 0.00 | -130.80 | -49.86 |
| X | 2.71 | 0.31 | 8.61 | 0.00 | 1.97 | 3.45 |
Рис. 14. Фрагмент регрессионного анализа
2.4. Экономический прогноз
Рассматриваемая модель 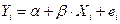
1) точечный прогноз фактора Х;
2) точечный прогноз показателя Y;
3) интервальный прогноз показателя Y.
Рассмотрим содержание этих этапов подробнее.
1) точечный прогноз фактора Хв зависимости от специфики исходных данных и условия задачи можно определить одним из следующих способов:
а) если исходные данные являются временными рядами, то для прогноза фактора можно воспользоваться методами экстраполяции и использовать наиболее подходящую модель временного ряда
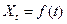
Тогда прогноз фактора на k шагов вперед определяется по формуле
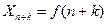
б)вслучае временных рядов 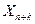
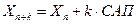
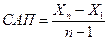
в)если исходные данные являются пространственными, то, очевидно, в задаче будет задано правило для определения 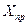
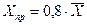
2) точечный прогноз показателя Yнаходят подстановкой в модель прогнозных значений фактора:
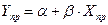
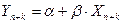
3) интервальный прогноз показателя Y:
вначале находят ошибку прогнозирования
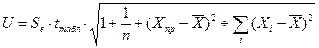
которая зависит от стандартной ошибки модели 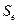
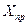
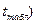
затем находят сам доверительный интервал прогноза:
нижняя граница интервала – 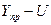
верхняя граница интервала – 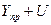
Пример (продолжение).
5) осуществить прогнозирование среднего значения показателя Y при уровне значимости 
1) точечный прогноз фактора Х
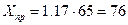
2) точечный прогноз показателя Y
3) интервальный прогноз показателя Y
Нижняя граница интервала: 115,66-17,97=97,69
Верхняя граница интервала: 115,66+17,97=133,63.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.