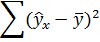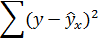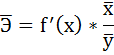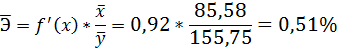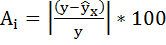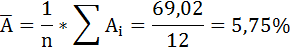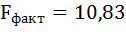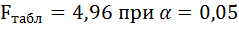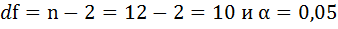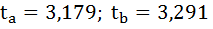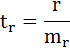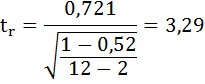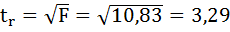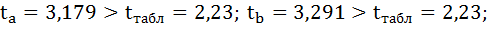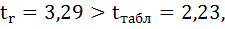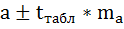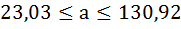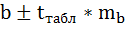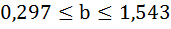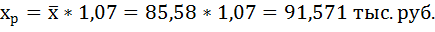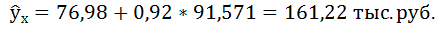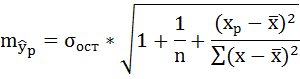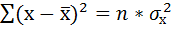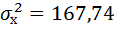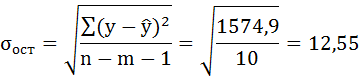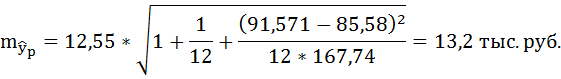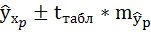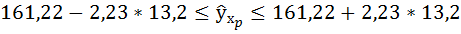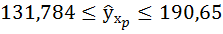рассчитать параметры линейной регрессии
Линейная регрессия
Линейная регрессия это способ описания зависимости между двумя или более исходными данными. При использовании линейная регрессии в математическом анализе можно узнать:
Зависимость одной переменной (y) от переменной(x), или нескольких других переменных.
На сколько значение (y) может изменяться в зависимости от значения (x).
На сколько значение (y) зависит от значения (x).
Появляется возможность предсказать значение (y) от значения (x).
Калькулятор расчета регрессии
Важно! В качестве разделителя для чисел используйте пробел
Предсказать значение Y при помощи линейной регрессии
Формулы
Как пользоваться калькулятором линейной регрессии
Самый простой способ понять что такое линейная регрессия, это объяснить все на конкретном примере.
За исходными данными обратимся к официальному сайту федеральной службы государственной статистики. Возьмем от туда размер средней пенсии в России за последние одиннадцать лет и введем эти числа в поле Y, (15400 14900 14300 13620 13132 11783 10888 10400 9040 8202 7476 5191). Теперь в поле X внесем соответствующие им года (2020 2019 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009).
Если вы хотите предсказать какое нибудь значение, тогда воспользуйтесь второй частью данного калькулятора. В поле «Введите X» поставьте год, в котором вы хотите узнать какой будет размер пенсии, затем нажмите «Вычислить». В поле «Значение Y» появится число, означающее размер пенсии в соответствующий период времени. Например если в поле «Введите X» поставим 2024 год, то узнаем какая средняя пенсия будет в этом году, она равна 19624 рублей.
Задача №3. Расчёт параметров регрессии и корреляции с помощью Excel
По территориям региона приводятся данные за 200Х г.
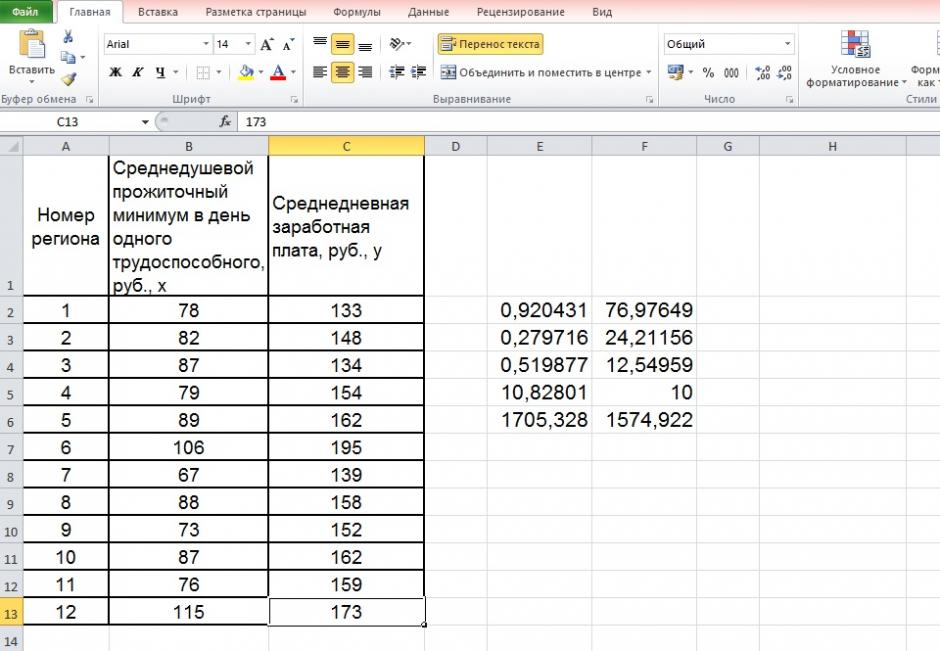
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии

3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
5. Оцените с помощью средней ошибки аппроксимации качество уравнений.
6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости 
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
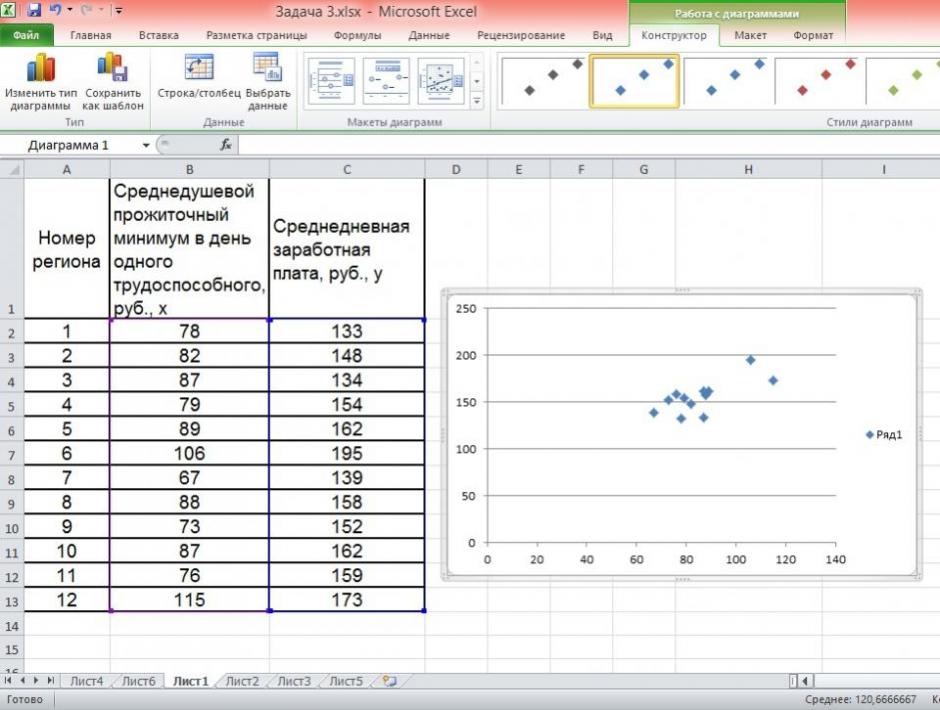
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
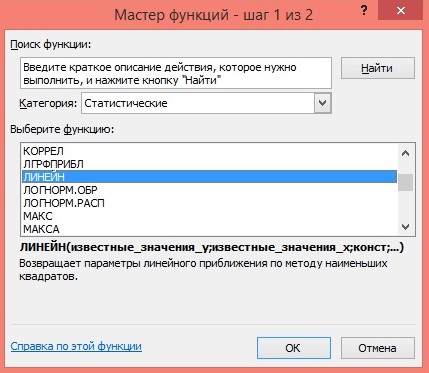
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
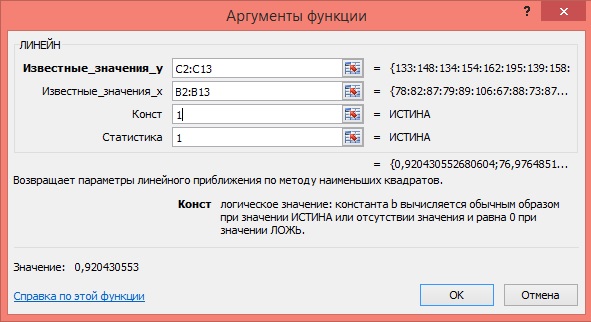
5) Заполните аргументы функции:
Известные значения у – диапазон, содержащий данные результативного признака;
Известные значения х – диапазон, содержащий данные факторного признака;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Коэффициент детерминации R 2 | Стандартная ошибка y |
| F-статистика | Число степеней свободы df |
| Регрессионная сумма квадратов |
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
По вычисленному коэффициенту детерминации 
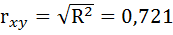
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой 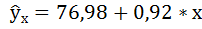
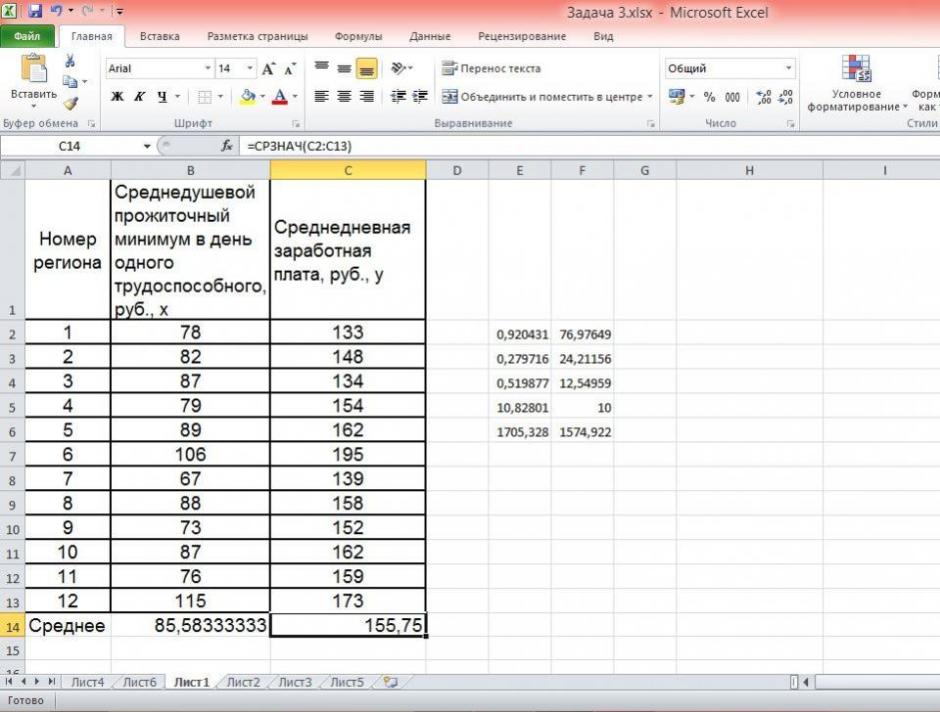
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные факторного признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист – можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
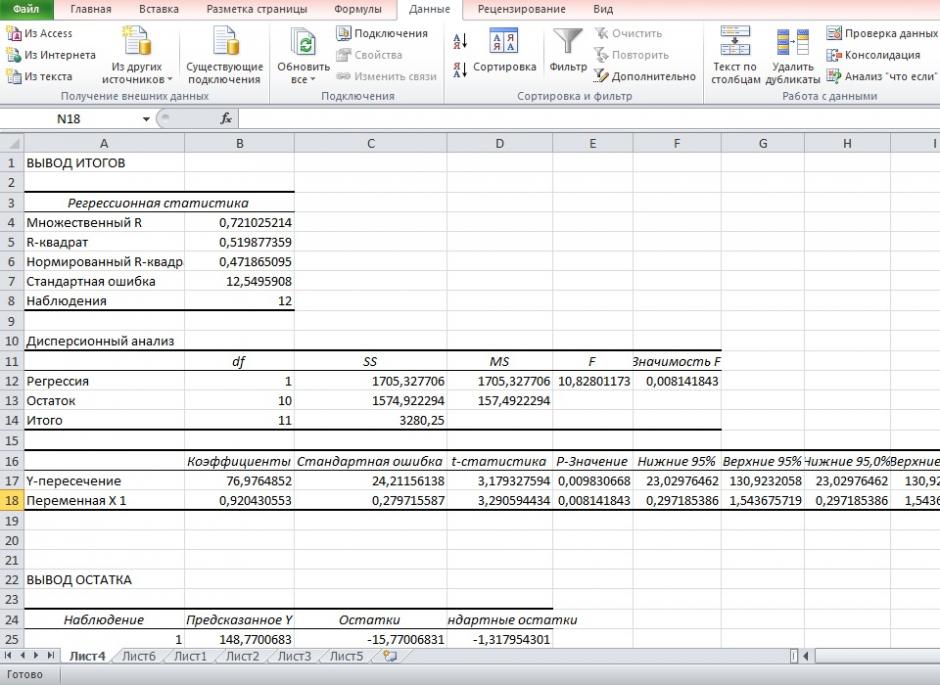
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
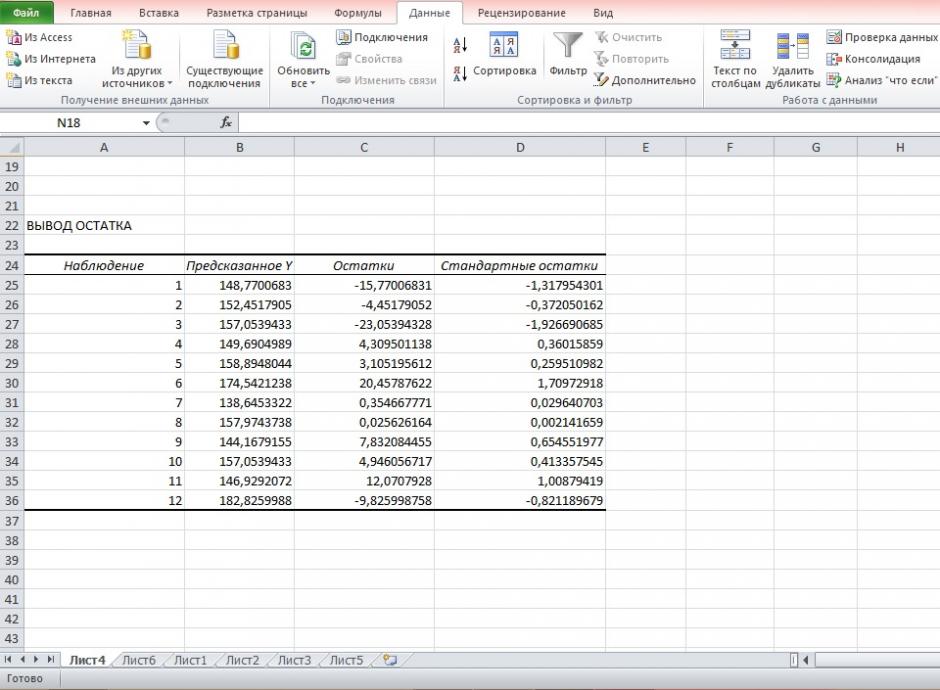
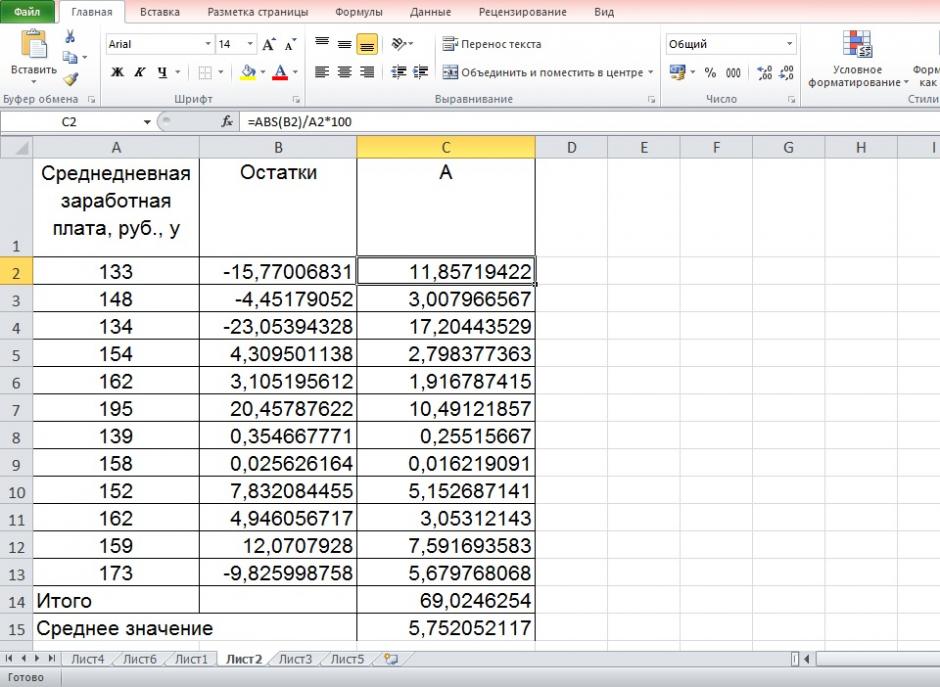
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как 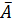
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку 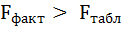
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля:
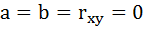
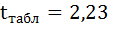
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ:
где 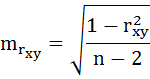
Данные для расчёта возьмём из таблицы на Рисунке 7.
II способ:
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 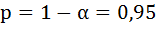
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
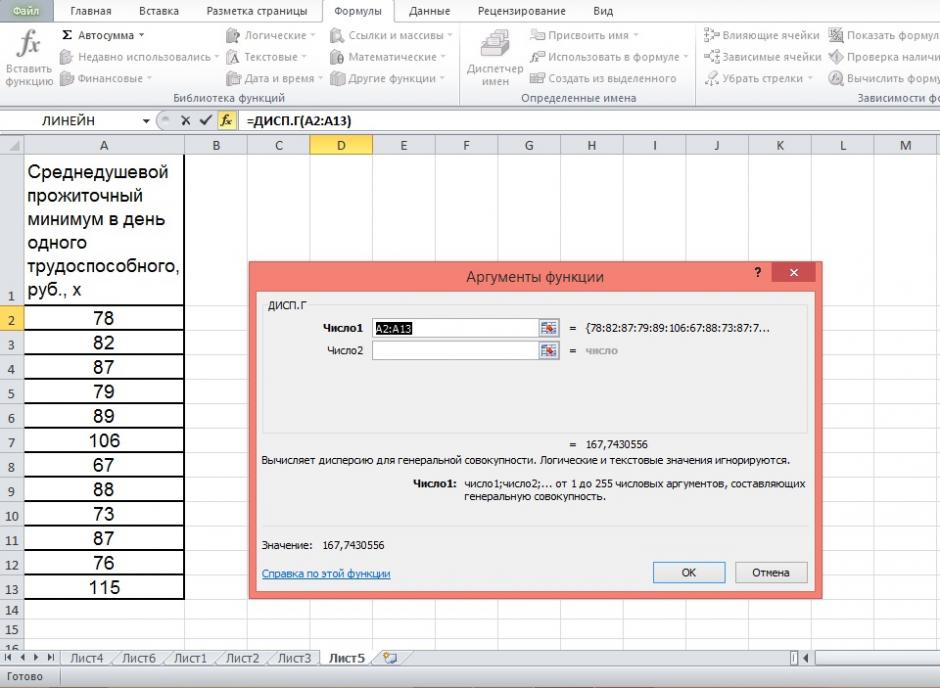
2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при 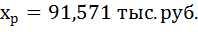
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.
Линейная регрессия
Линейная регрессия (Linear regression) — это это математическая модель, которая описывает связь нескольких переменных. Модели линейной регрессии представляют собой статистическую процедуру, помогающую прогнозировать будущее. Она применяется в научных сферах и в бизнесе, а в последние десятилетия используется в машинном обучении.
Для чего нужна линейная регрессия
Задача регрессии в машинном обучении — это предсказание одного параметра (Y) по известному параметру X, где X — набор параметров, характеризующий наблюдение.
Как работает линейная регрессия
Возьмем небольшой набор данных. Предположим, что это группа коттеджей, расположенных в одном районе. На оси Х обозначена их площадь, а на оси Y — рыночная стоимость. Чтобы увидеть, как стоимость дома зависит от его площади, построим регрессию.
Это будет простая линейная регрессия с одной переменной. Изменится площадь дома — изменится и стоимость. Для вычисления используем стандартное уравнение регрессии: f (x) = b + m⋅x, где m — это наклон линии, а b — ее сдвиг по оси Y. То есть изменение коэффициентов m и b будет влиять на расположение прямой:
Провести прямую линию через все точки на графике не получится, если они расположены в хаотичном порядке. Поэтому с помощью линейной регрессии определяется оптимальный вариант расположения этой прямой. Некоторые точки все равно останутся на расстоянии, но оно должно быть минимальным. Расчет этого минимального расстояния от прямой до каждой точки называется функцией потерь.
Для оценки точности регрессии используют разные метрики, например MSE (от англ. mean squared error — средняя квадратическая ошибка). Чем ниже MSE, тем лучше модель.
В первом случае MSE будет равна 0,17, во втором — 0,08, а в третьем — 0,02. Получается, что третья прямая лучше всего показывает зависимость цены дома от его площади.
Data Scientist с нуля
Получите востребованные IT-навыки за один год и станьте перспективным профессионалом. Мы поможем в трудоустройстве. Дополнительная скидка 5% по промокоду BLOG.
Расчет линейной регрессии в Python
Построим регрессию, чтобы узнать, как кассовые сборы фильма зависят от бюджета, который вложили в его производство.
Для расчета понадобится csv-файл, который содержит информацию о бюджетах и сборах 5 034 фильмов, которые когда-то выходили в прокат. Эти данные станут базой для исследования.
Построим модель линейной регрессии с помощью Python. Для этого нужно импортировать несколько библиотек:
Модель линейной регрессии, которую нужно будет обучить, импортируется с помощью библиотеки sklearn. В качестве X будет колонка production_budget_usd, а в качестве Y – колонка worldwide_gross_usd.
На основе этих данных определяется нужный наклон прямой и расположение относительно осей координат. Это и будет нужной линейной регрессией, по которой можно предсказать сборы собственного фильма, выбрав подходящий бюджет.
В итоге получится график того, как соотносятся бюджеты и кассы у фильмов в списке. Каждая точка — это отдельная кинолента. На оси Х показаны затраты на производство, а на оси У — сколько она заработала. Теперь через эти точки нужно провести прямую так, чтобы она была максимально близка ко всем точкам на графике.
Множественная линейная регрессия
В жизни кассовые сборы кино зависят не от одной переменной, а от совокупности разных факторов: популярности жанра, режиссера, каста актеров и затрат на промокампанию. Если рассчитать все факторы, влияющие на сборы, то уравнение изменится:
Стало f(x) = b + m1*x1 + … + mn*xn
Каждый коэффициент в нем показывает важность признаков. То есть множественная регрессия демонстрирует, как каждый параметр влияет на расположение прямой, и выбирает оптимальный вариант точно так же, как и линейная — с помощью функции потерь.
Data Scientist с нуля
Получите востребованные IT-навыки за один год и станьте перспективным профессионалом. Мы поможем в трудоустройстве. Дополнительная скидка 5% по промокоду BLOG.
Рассчитать параметры линейной регрессии
Параметры уравнения y = a*x + b
а) с помощью статистической функции ЛИНЕЙН (Excel). Получаем следующую статистику:
| a | 0,15 | 197,80 | b |
| ma | 0,07 | 13,77 | mb |
| R 2 | 0,32 | 8,36 | Sост |
| Fф | 5,07 | 11 | Ч.С.С |
| 354,56 | 768,52 | (y-y x ) 2 |
Записываем уравнение парной линейной регрессии:
Экономический смысл уравнения: с увеличением х на 1 ед., y возрастает в среднем на а ед.
Если требуется рассчитывать без применения Excel, то строим таблицу.
| N | x | y | x 2 | x*y | (y-y x ) 2 | (y-y ср ) 2 |
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| N | ||||||
| Итого | ||||||
| Среднее |
б) для парной линейной регрессии:
в) или решая систему уравнений
Для автоматического расчета можно воспользоваться сервисом Уравнение регрессии
б) с помощью статистической функции КОРРЕЛ (Excel)
Это означает, что в среднем, расчетные значения зависимого признака отклоняются от фактического значения на А%.
а) с помощью функции ЛИНЕЙН (Excel)
Оценка статистической значимости
а) по критерию Фишера :
1. Выдвигаем нулевую гипотезу о статистической незначимости параметров регрессии и показателя корреляции а = b = r xy
2. Фактическое значение критерия получено из функции ЛИНЕЙН (Excel)
4. Сравниваем фактическое и табличное, значения критерия F факт > F табл
нулевую гипотезу отклоняем и делаем вывод о статистической значимости и надежности полученной модели.
б) по критерию Стъюдента
1. Выдвигаем нулевую гипотезу о статистически незначимом отличии показателей от нуля; а = b = r xy =0;
2. Табличное значение t-критерия зависит от числа степеней свободы и заданного уровня значимости а.
3. Фактические значения t-критерия рассчитываются отдельно для каждого параметра модели. С этой целью, сначала определяются случайные ошибки параметров ma, mb, mr
Рассчитаем фактические значения t-критерия.
4. Сравниваем фактические значения t-критерия с табличными значением:
в) чтобы рассчитать доверительный интервал для параметров регрессии a,b необходимо определить предельную ошибку параметров:
4. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Прогнозное значение yp определятся путем подстановки в уравнение регрессии соответствующего прогнозного значения хр. Если прогнозное значение составит хр = ∙1,1, то прогнозное значение y
5. Рассчитаем случайную ошибку прогноза:
Предельная ошибка прогноза: ∆y = tтабл*myp
Доверительный интервал прогноза:
С надежностью 0,95 прогнозное значение y заключено в данном доверительном интервале. Поскольку границы не принимают нулевых значений можно сделать вывод о статистической надежности прогноза.
Автоматический расчет
Для автоматического расчета можно воспользоваться сервисом Уравнение регрессии. Необходимо будет ввести значения x,y (можно вставить из MS Excel). Решение оформляется в файле MS Word с пояснением нахождения каждого параметра.