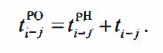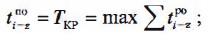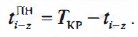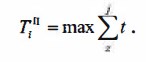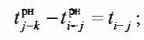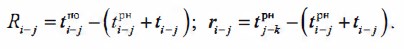рассчитать параметры сетевой модели табличным методом
Табличный метод расчета параметров сетевой модели.



Принципиальное отличие табличного метода расчета от графического заключается в том, что он позволяет расcчитать параметры сетевой модели непосредственно в таблице, в которую предварительно заносятся в определенном порядке все работы и их продолжительность.
При расчете определяются:
поздний срок окончания работы tпoij.
Резервы времени работы:
частный резерв второго вида Р»nij.
На основе производственного расчета параметров сети определяется критический путь сетевой модели и его продолжительность.
Ниже приводятся правила для определения параметров сети.
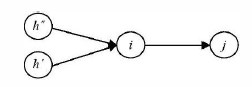
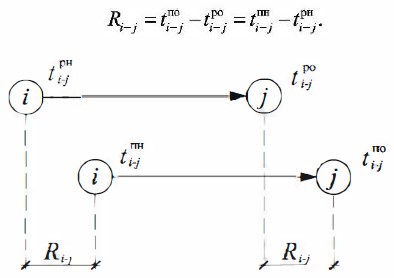
ПРАВИЛО 1. Для определения времени первого начала данной работы tpHij рассматриваются все работы, входящие в начальное событие данной работы. Из графы tpo входящих работ выбирается максимальное время раннего окончания (tpo)max, которое переносится в графу tpнij данной работы.
ПРАВИЛО 2. Время раннего окончания tpoij равно времени раннего начала этой работы плюс ее продолжительность:
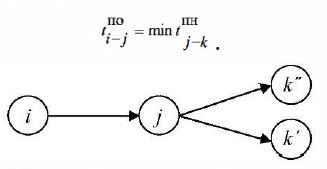
ПРАВИЛО 3. Для нахождения времени позднего окончания данной работы tпoij рассматриваются все работы, выходящие из конечного события данной работы. Из графы tпн выходящих работ выбирается минимальное время раннего окончания (tpo)max, которое переносится в графу tno данной работы (расчет ведется с низу вверх).
Если в завершающее событие входят две или несколько работ, то время окончания этих работ определяется максимальным значением их раннего окончания.
ПРАВИЛО 4. Время позднего начала данной работы tпнij равно времени окончания этой работы tпoij минус ее продолжительность:
ПРАВИЛО 5. полный резерв времени работы Pnij определяется разницей между поздним и ранним началом этой работы:
Либо разностью между поздним и ранним окончанием этой работы:
ПРАВИЛО 6. Для определения частного резерва первого вида данной работы Pnij рассматриваются работы, имеющие то же начальное событие. Из графы tпн этих работ выбирают минимальное время позднего начала, которое вычитается из времени позднего начала данной работы.
Если из события выходит одна работа, то частный резерв первого вида этой работы равен 0.
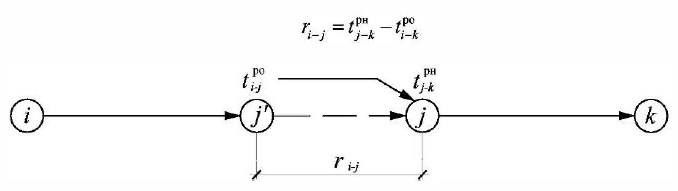
ПРАВИЛО 7. Для определения частного резерва времени второго вида данной работы P»nij рассматриваются работы, имеющие одинаковые конечные события. Из графы tpo этих работ выбирается максимальное время раннего окончания, из которого вычитают время раннего окончания данной работы.
Если в событие входит одна работа, то частный резерв времени второго вида этой работы равен 0.
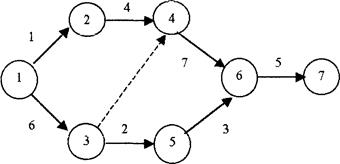
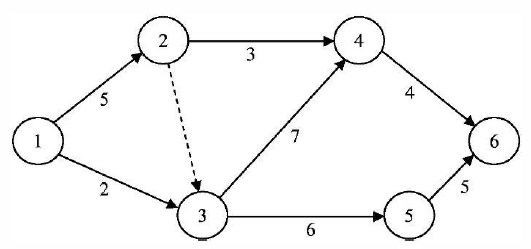
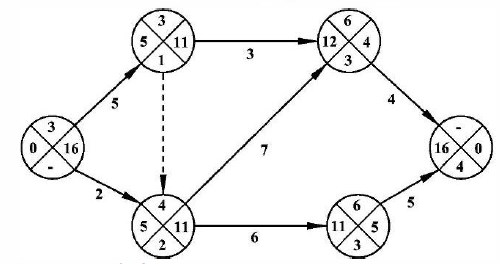
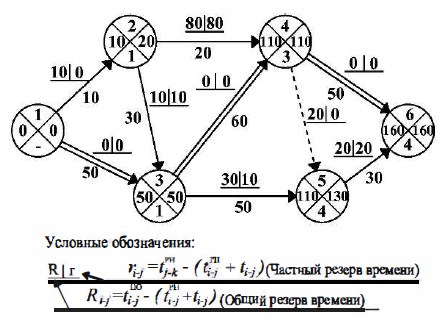
Произведем расчет представленной на рис. 22 сетевой модели с помощью приведенных выше правил. Продолжительность работ указана в неделях.
Рисунок 22
Указанные выше параметры сети определяются в следующем порядке.
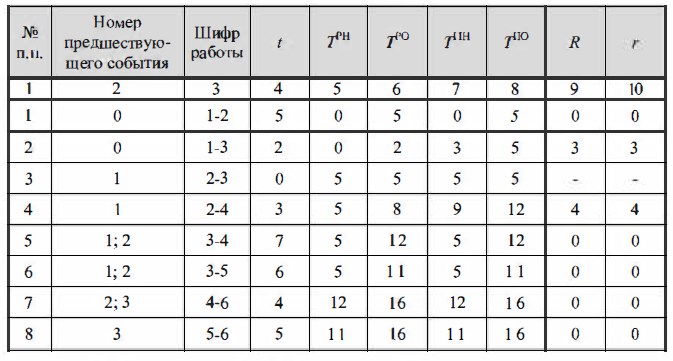
1 ЭТАП. По данным сетевой модели заполняются графы 2, 3, 1 и 4 табл. 1. В графу 1 записывается количество работ, непосредственно входящих в начальное событие данной работы.
После заполнения указанных граф весь расчет ведется в таблице без использования сетевой модели.
2 ЭТАП. Определяется раннее начало и окончание работ, т.е. заполняются графы 5 и 6 табл.1. Раннее начало работ с начальным событием, являющимся в то же время исходным событием данной сетевой модели, принимается равным 0: tpнij= 0.
Таблица 1
| Количество предшеств. работ | Код работы | Продолжит. работы в днях | Раннее начало работ | Раннее окончание работ | Позднее начало работ | Позднее окончание работ | Резервы времени работ |
| Начальн. событие | Конечн. событие | полный | Первого Вида. | второго вида |
Следовательно в графу 5 для работы 1, 2 и 1, 3 записываем 0.
Раннее окончание работы 4,6 равно:
графа 6(tpo4,6) = графа 5(tpн4,6) + графа 4(t4,6).
Аналогично выполнены расчеты ранних сроков начала и окончания последующих работ.
Полученные данные сведены в таблице 1.
3 ЭТАП. Определяется время последнего окончания и начала работ, т.е. заполняются графы 7 и 8 табл.1. Расчет при этом ведется с последней строки таблицы снизу вверх.
Расчет поздних сроков начинается с определения позднего срока окончания работы, имеющей максимальное раннее окончание.
Поздний срок окончания этой работы принимается равным ее раннему сроку окончания, т.е. tnoic = tpoic.
В нашем примере такой работой является работа 6,7, принимаем tno6,7 = tpo6,7 =18 неделям.
В нашем примере время позднего окончания работы 6,7 равно:
Определим поздние сроки начала и окончания работы 5,6, в соответствии с правилом 3. Для определения tpo5,6 в графике 2 ищем работы выходящие из конечного (6) события данной работы. Такой работой является работа 6,7. Из графы 7 переносим значение tпн6,7=13 неделям, в графу 8 работы 5,6, т.е. tпo5,6 = 13 неделям. Позднее начало работы 5,6 соответственно равно:
Аналогичные расчеты проведены для работ 4,6; 3,5; 3,4; 2:4.
Рассмотрим порядок определения поздних сроков начала и окончания работы 1,3.
В соответствии с правилом 3 для определения tpol,3 в графике 2 ищем работы, выходящие из конечного события данной работы.
Такими работами являются работы 3,4 и 3,5.
Затем заполняем графу 6. Раннее окончание работы 1,2 равно сумме раннего начала этой работы и ее продолжительности, т.е.
tpol,2 = tпн1,2 + tl,2 =0+1=1.
Таким же образом определяется раннее окончание работы 1,3:
tpol,3= tpнl,3+ tl,3= 0 + 6= б
Для определения раннего начала всех остальных работ воспользуемся правилом 1.
Для нахождения tрн2,4 в графе 3 табл.1 ищем работы, входящие в начальное (2) событие данной работы. Такой работой является работа 1,2.
Из графы 6 переносим значение tpol,2 = 1 неделе в графу 5 работы 2,4, т.е. tpн2,4 = 1 неделе. Раннее окончание работы 2,4 равно сумме раннего начала работы и ее продолжительности:
tpo2,4 = tpн2,4 +t2,4 =1+4=5 неделям.
Этот расчет проводится только для пояснения метода. Обычно все расчеты выполняются непосредственно в таблице. Например, для работы 2,4 графа 5[tpн2,4] + графа 4[t2,4] = графа 6[tpo2,4].
Для определения 1рн3,4 в графе 3 табл.1 ищем работы, входящие в начальное событие данной работы.
Такой работой является работа 1,3.
Из графы б переносим значение Тро1,3 = 6 неделям в графу 5 работы 3,4, т.е. tрн3,4 = б неделям.
Раннее окончание работы 3,4 соответственно равно:
графа 5[tpн3,4] + графа 4[t3,4] = графа 6[tpo3,4].
Аналогично определены tрн3,5 и tpo3,5. Далее определим tрн4,б и tpo4,6. В соответствии с правилом 1 для нахождения в графе 3 ищем работы, входящие в начальное (4) событие данной работы. Такими работами являются работы 2,4 и 3,4.
В графе 6 находим для этих работ время раннего окончания, которые соответственно равны:
В графе 7 для этих работ находим времена позднего начала, которые соответственно равны (табл. I):
Выбираем минимальное время позднего начала [в данном случае (tпн)min = б неделям], которое переносим в графу 8 работы 1,3, т.е. tпоl,3 = 6 неделям.
Позднее начало работы соответственно равно:
Аналогичные расчеты проведены и для работы 1,2. Все данные сведены в таблице 1.
4 ЭТАП. Определяется полный резерв времени работ, т.е. заполняется графа 9. Полные резервы времени работ равны (см. правило 5):
5 ЭТАП. Определяются работы, лежащие на критическом пути.
Из определения критического пути следует, что работы, лежащие на критическом пути, не имеют резерва времени, т.е. работы, имеющие нулевой полный резерв работы времени, находятся на критическом пути.
Из этого следует, что в нашем примере критический путь проходит через следующие работы 1,3; 3,4; 4,6; 6,7.
6 ЭТАП. Определяется частный резерв времени работ первого вида.
Частные резервы времени работ первого вида (см. правило 6).
P’n2,4 = 0 (см. правило 6)
P’n4,6 = 0; P’n5,6 = 0; P’n6,7 = 0.
7 ЭТАП. Определяется частный резерв времени работ второго вида (см. правило 7):
18.3 Расчет сетевых графиков
Расчет сетевых графиков сводиться к численному определению его пара-метров. Поэтому сначала перечислим их.
При расчете сетевых графиков определяются следующие параметры:
— ранние начала и окончания работ;
— поздние начала и окончания работ;
— продолжительность критического пути;
— общие и частные резервы работ.
Рис. 18.8 Расчетная модель
Раннее начало работы (рис. 18.9) равно продолжительности максимального пути от исходного события графика до начального события данной работы:
Рис. 18.9 Модель расчета ранних начал
Для начальных (исходных) работ:
— раннее начало принимается равным 0;
— раннее окончание численно равно продолжительности работы. Максимальное раннее окончание одной из завершающих работ определяет продолжительность критического пути.
Позднее окончание работы определяется разностью между продолжительностью критического пути и продолжительностью максимального пути от конечного события данной работы до завершающего события графика.
Позднее окончание любой работы (рис. 18.1 О) равно наименьшему из поздних начал последующих работ:
Рис. 18.10 Модель расчета поздних окончаний
Позднее начало работы равно разности между величинами ее позднего окончания и продолжительности.
Для завершающих работ сетевого графика:
— позднее окончание равно величине продолжительности критического пути:
= позднее начало завершающей работы равно разности между продолжительностью критического пути и продолжительностью данной работы:
Рис. 18.11 Модель расчета общих резервов
Рис. 18.12 Модель расчета частных резервов
Частный резерв времени отличается от нуля, если в конечное событие работы входят две и более работы.
Методы расчета сетевых графиков
Классическим методом, положившим начало теории расчета сетевых графиков, является табличный метод, или, как говорят, алгоритм расчета сетевого графика по таблице.
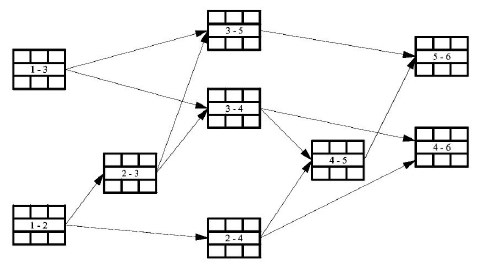
Пример графика для расчета табличным методом приведен на рис. 18.13. В этом случае определение параметров сетевого графика выполняется в таблице.
Рис. 18.13 Пример графика для расчета табличным методом и методом потенциалов
Заполнение таблицы ведется в следующем порядке.
2) Производят расчет ранних параметров работ построчно сверху вниз.
3) Определяют продолжительность критического пути, равная максимальному из ранних окончаний завершающих работ.
4) Рассчитывают поздние параметры работ. Расчет ведется построчно снизу вверх, от завершающих работ до исходных.
5) Определяют общие и частные резервы времени (их можно определить по каждой работе вразбивку).
Определяют перечень работ, составляющих критический путь, т.е. работ, не имеющих резервов времени.
При расчете сетевых графиков табличным методом заполняют следующую таблицу (табл. 18.1).
Расчет сетевого графика
В графу 3 заносят шифр (код) каждой работы, запись ведут последовательно, начиная с первого события. Когда из события выходят несколько работ, запись ведут в порядке возрастания номеров их конечных событий. После этой процедуры в графу 2 записывают номера событий, предшествующих каждой работе.
Следующей заполняют графу 4. Против каждой работы, записанной в графе 3 из сетевого графика, проставляют её продолжительность t.
Максимальное раннее окончание последней работы равно величине критического пути.
Дальше заполняют графы 7 и 8. Позднее начало ТПН и окончание ТПО записываем в таблицу 18.1, начиная с конца графы.
Критический путь, а следовательно, и позднее окончание завершающей работы, равен 16 дням. Вносим эту цифру в строку 8 графы 8. Позднее начало работы равно разности его позднего окончания и продолжительности.
Общий резерв R (графа 9) определяют как разность между числами в графах 8 и 6 или 7 и 5.
Частный резерв r (графа 10) подсчитывают как разность между ранним началом последующей работы и ранним началом данной. При заполнении данной графы необходимо учитывать следующее, если в конечное событие данной работы входит только одна стрелка, то частный резерв ее равен нулю. Для работ, не лежащих на критическом пути, но входящих в события, лежащие на нем, общие и частные резервы численно равны. Частные и общие резервы работ, лежащих на критическом пути, равны нулю.
Правильность расчета сетевого графика подтверждают проверкой:
— ранние параметры никогда не превосходят по численному значению поздние параметры;
— критический путь должен представлять собой непрерывную последовательность работ от исходного события до завершающего;
— величина частного резерва времени работы не должна превосходить величину общего резерва времени;
— позднее начало одной из исходных работ обязательно должно быть нулевым.
Расчет сетевых графиков методом потенциалов
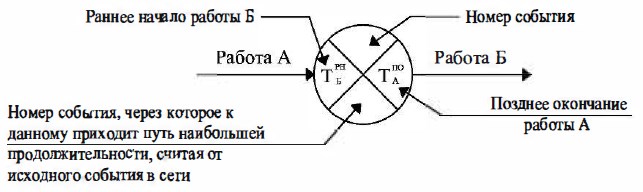
Потенциалом i-го события (ТjП ) называют величину наиболее продолжительного пути от данного события до завершающего:
Потенциал события (рис. 18.14) показывает, сколько дней осталось от данного события до завершения всех работ планируемой программы. Потенциал определяют последовательно, начиная от завершающего события сети.
В качестве примера рассмотрим тот же график, размещенный на рис. 18.13. Расчет (рис. 18.15) начинают с завершающего события 6, потенциал которого равен О. В верхний сектор ставим прочерк, в правый записываем О и переходим к последующему событию.
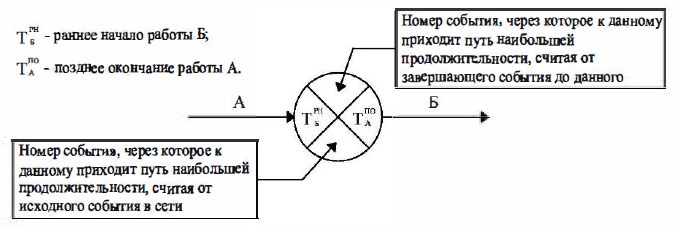
Рис. 18.14 Запись в секторах при расчете методом потенциалов
Рис. 18.15. Пример расчета методом потенциалов
( номера событий соответствуют рис. 18.1 З)
+ 3 = 7; выбирают наибольшее значение 11. Аналогичным образом рассчитывают остальные события. Потенциал исходного события составляет 16 дней, т.е. равен величине критического пути.
Зная потенциал события, позднее окончание работ можно определить по формуле
Поскольку ранние начала работ записаны в левых секторах, а на графике показаны продолжительности работ, по уже приведенным формулам частного и общего резерва времени можно определить их значение.
Изменения, возникающие в ходе выполнения работ, не влияют на потенциалы последующих событий; поэтому оперативный пересчет графика занимает мало времени. В этом заключается главное преимущество расчета методом потенциалов.
При этом методе каждое событие (рис. 18.16) графиком делится на 4 сектора, в которых указываются необходимые расчетные данные.
Рис. 18.16 Условные обозначения при четырехсекторном методе расчета
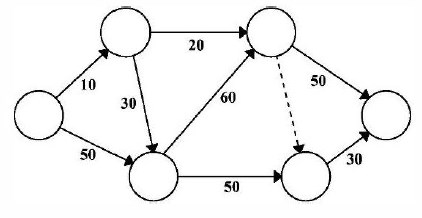
Исходным графиком для расчета четырехсекторным методом служит график, приведенный на рис. 18.17.
Рис. 18.17 Исходный график для расчета четырехсекторным методом
Вначале от исходного события до завершающего определяют все ранние начала работ.
Для завершающего события графика значения в левом и правом секторах равны, поскольку максимальное из ранних окончаний завершающей работы равно позднему окончанию этой работы.
Затем рассчитывают поздние окончания работ от завершающего к начальному событию. Рассчитанный график будет иметь вид показанный на рис. 18.18.
Дополнительным требованием к критическим работам является требование по соблюдению условия
20-12 = 8; 25-5 = 20; 25-11 = 12; следовательно, работы нижнего пути- некритические.
Рис. 18.18 График, рассчитанный четырехсекторным методом
Резервы времени работ графика можно отметить на самом графике в виде Rr, а рассчитать их следует по формулам:
Четырехсекторный способ расчета сетевых графиков позволяет быстрее осуществить расчет и определить продолжительность критического пути (иногда требуется прикидочный расчет), но при повторном расчете требуется перебирать данные на графике. Этого не требуется при табличном способе, где пересчитывается сама таблица. Кроме того, в таблице наглядно прослеживаются все без исключения параметры сетевого графика (включая резервы времени).
Построение сетевых графиков «вершины-работы»
В последнее время построение сетевых графиков всё чаще выполняют по принципу «вершины-работы», а не по принципу «вершины-события», как это было в предыдущих примерах (рис.18.19).
Раннее начало последующей работы равно раннему окончанию предыдущей работы. Если работе непосредственно предшествует несколько работ, то ее раннее начало будет равно максимальному значению из ранних окончаний предшествующих работ.
Рис. 18.19 График типа «вершины-работы»
Рис. 18.20 Изображение работы в сетевом графике «вершины-работы»
Раннее окончание завершающей работы определяет продолжительность критического пути.
Расчет поздних сроков ведут в обратном порядке, от завершающей работы до исходной. Позднее окончание завершающей работы равно ее раннему окончанию, т.е. продолжительности критического пути.
Позднее начало определяют как разность позднего окончания и продолжительности работы.
Полный ( общий) резерв времени, равный разности поздних и ранних сроков, заносят в числитель середины нижней части.
Частный резерв времени, равный разности между минимальным ранним началом последующих работ и ранним окончанием данной работы, записывают в знаменатель середины нижней части.
Частный резерв всегда меньше полного резерва работы или равен ему. Последовательность работ с нулевыми резервами времени является критическим путем сетевого графика.
Табличный метод расчета параметров сетевой модели
Принципиальное отличие табличного метода от графического заключается в том, что он позволяет рассчитать параметры сетевой модели непосредственно в таблице, в которую предварительно заносятся в определенном порядке все работы и их продолжительность.
При расчете определяются:
поздний срок начала работы – tnнij;
резервы времени работы:
частный резерв первого вида – Р’nij,
частный резерв второго вида – Р”nij.
На основе производственного расчета параметров сети определяется критический путь сетевой модели и его продолжительность.
Ниже приводятся правила для определения параметров сети.
Правило 1. Для определения времени первого начала данной работы tрнij рассматриваются все работы, входящие в начальное событие данной работы. Из графы tро входящих работ выбирается максимальное время раннего окончания (tро)max, которое переносится в графу tрнij данной работы.
Правило 2. Время раннего окончания работы tpojj равно времени раннего начала этой работы плюс ее продолжительность:
Правило 3. Для нахождения времени позднего окончания данной работы tnоij рассматриваются все работы, выходящие из конечного события данной работы. Из графы tnн выходящих работ выбирается минимальное время позднего начала (tnн)min, которое переносится в графу tnо данной работы (расчет ведется снизу вверх).
Если в завершающее событие входят две или несколько работ, то время окончания этих работ определяется максимальным значением их раннего окончания.
Правило 4. Время позднего начала данной работы tnнij равно времени позднего окончания этой работы tnoij минус ее продолжительность :
Правило 5. Полный резерв времени работы Рnij определяется разностью между поздним началом этой работы:
либо разностью между поздним и ранним окончанием этой работы:
Правило 6. Для определения частного резерва первого вида данной работы Р’nij рассматриваются работы, имеющие то же начальное событие. Из графы tnн этих работ выбирают минимальное время позднего начала, которое вычитается из времени начала данной работы.
Если из события выходит одна работа, то частный резерв первого вида этой работы равен 0.
Правило 7. Для определения частного резерва времени второго вида данной работы Р”nij рассматриваются работы, имеющие одинаковые конечные события. Из графы tpo этих работ выбирается максимальное время раннего окончания, из которого вычитают время раннего окончания данной работы.
Если в событие входит одна работа, то частный резерв времени второго вида этой работы равен 0.
Произведем расчет представленной на рисунке 16 сетевой модели с помощью приведенных выше правил. Продолжительность работ указана в неделях.
 |
Указанные выше параметры сети определяются в следующем порядке.
1 этап. По данным сетевой модели заполняются графы 2,3,1 и 4 таблицы 1. В графу 1 записывается количество работ, непосредственно входящих в начальное событие данной работы.
После заполнения указанных граф весь расчет ведется в таблице без использования сетевой модели.
2 этап. Определяется раннее начало и окончание работ, т.е. заполняются графы 5 и 6 таблицы 1. Раннее начало работ с начальным событием, являющимся в то же время исходным событием данной сетевой модели, принимается равным нулю: tpнij= 0.
Практика построения сетевого графика
Представим себе ситуацию развития проекта капитального строительства на производственном предприятии. Проект успешно инициирован и полным ходом идут работы по его планированию. Сформирована и утверждена иерархическая структура работ, план по вехам принят. Разработан первичный вариант календарного плана. Поскольку задача оказалась достаточно масштабной, куратор принял решение о разработке еще и сетевой модели. Расчет сетевого графика в прикладном аспекте его исполнения является предметом настоящей статьи.
Перед стартом моделирования
Методологический базис сетевого проектного планирования представлен на нашем сайте несколькими статьями. Я лишь сошлюсь на две из них. Это материалы, посвященные этапу сетевого планирования проекта в целом и непосредственно моделированию сетевого графика проекта. Если в ходе повествования у вас будут возникать вопросы, просмотрите ранее представленные осмысления, основная суть методологии в них изложена. В настоящей статье мы рассмотрим небольшой пример локальной части комплекса строительно-монтажных работ в рамках значительной проектной реализации. Расчеты и моделирование будем выполнять методом «вершина-работа» и классическим табличным способом («вершина-событие») с применением МКР (метода критического пути).
Построение сетевого графика мы начнем на основе первой итерации календарного плана, выполненного в форме диаграммы Ганта. Для целей наглядности предлагаю не учитывать отношения предшествования и максимально упростить последовательность действий. Хотя на практике такое бывает редко, представим в нашем примере, что операции выстроены в последовательность вида «окончание-начало». Ниже вашему вниманию представляются две таблицы: выписка из списка работ проекта (фрагмент из 15-ти операций) и список параметров сетевой модели, необходимый для представления формул.
Пусть вас не пугает обилие элементов. Построение сетевой модели и расчет параметров достаточно просто выполнить. Важно тщательно подготовиться, иметь под рукой иерархическую структуру работ, линейный график Ганта – в общем, все, что дает возможность определиться с последовательностью и взаимосвязями действий. Еще в первые разы выполнения графика я рекомендую иметь перед собой формулы расчета требуемых значений. Они представлены ниже.
Что нам потребуется определить в ходе построения графика?
Последовательность действий по моделированию
Шаг первый
Построение сетевого графика начинаем путем размещения прямоугольников задач последовательно слева-направо, применяя правила, описанные в предыдущих статьях. При выполнении моделирования методом «вершина-работа» основным элементом диаграммы выступает семисегментный прямоугольник, в составе которого отражены параметры начала, окончания, длительности, резерва времени и наименования или номера операций. Схема представления ее параметров показана далее.
В соответствии с логикой последовательности операций с помощью специализированной программы, MS Visio или любого редактора размещаем образы работ в заданном выше формате. В первую очередь заполняем наименования выполняемых действий, их номера и длительность. Рассчитываем раннее начало и раннее окончание с учетом формулы раннего начала текущего действия в условиях нескольких входящих связей. И так проходим до завершающей фрагмент операции. При этом, в нашем примере проекта тем же графиком Ганта не предусмотрены исходящие связи от операций 11, 12, 13 и 14. «Подвешивать» их на сетевой модели недопустимо, поэтому мы добавляем фиктивные связи к конечной работе фрагмента, выделенные на рисунке синим цветом.
Шаг второй
Находим критический путь. Как известно, это путь, имеющий самую большую продолжительность действий, которые в него входят. Просматривая модель, мы выбираем связи между работами, имеющими максимальные значения раннего окончания действий. Намеченный критический путь выделяем стрелочками красного цвета. Полученный результат представлен на промежуточной схеме далее.
Шаг третий
Заполняем значения позднего окончания, позднего начала и полного резерва работ. Для выполнения расчета переходим к конечной работе и берем ее за последнюю операцию критического пути. Это означает, что поздние значения окончания и начала идентичны ранним, и от последней операции фрагмента мы начинаем двигаться в обратную сторону, заполняя нижнюю строку схематического представления действия. Модель выполнения расчета показана ниже на схеме.
Шаг четвертый
Четвертым шагом алгоритма сетевого моделирования и расчетов выполняется вычисление резервов и коэффициента напряженности. Первым делом имеет смысл обратить внимание на полные резервы путей некритических направлений (R). Они определяются путем вычитания из продолжительности критического пути временной длительности каждого из этих путей, пронумерованных на схеме итогового сетевого графика.
Дополнительные расчеты модели
Выполнение расчета общего резерва текущей операции производится путем вычитания из значения позднего начала раннего начала или из позднего окончания раннего окончания (см. схему расчета выше). Общий (полный) резерв показывает нам возможность начала текущей работы позже или увеличения продолжительности на длительность резерва. Но нужно понимать, что пользоваться полным резервом следует с большой осторожностью, потому что работы, стоящие от текущего события дальше остальных, могут оказаться без запаса времени.
Помимо полных резервов в сетевом моделировании оперируют также и частными или свободными резервами, которые представляют собой разницу между ранним началом последующей работы и ранним окончанием текущей. Частный резерв показывает, есть ли возможность сдвинуть ранее начало операции вперед без ущерба для начала следующей процедуры и всему графику в целом. Следует помнить, что сумма всех частных резервных значений тождественна полному значению резерва для рассматриваемого пути.
Главной задачей выполнения вычислений различных параметров является оптимизация сетевого графика и оценка вероятности выполнения проекта в срок. Одним из таких параметров является коэффициент напряженности, который показывает нам уровень сложности реализовать работу в намеченный срок. Формула коэффициента представлена выше в составе всех расчетных выражений, применяемых для анализа сетевого графика.
Коэффициент напряженности определяется как разница между единицей и частного от деления полного резерва времени работы на разницу длительности критического пути и особого расчетного значения. Это значение включает ряд отрезков критического пути, совпадающих с максимально возможным путем, к которому может быть отнесена текущая операция (i-j). Далее помещен расчет частных резервов и коэффициентов напряженности работ для нашего примера.
Коэффициент напряженности варьируется от 0 до 1,0. Значение 1,0 устанавливается для работ, находящихся на критическом пути. Чем ближе значение некритической операции к 1,0, тем труднее удержаться в плановых сроках ее реализации. После того, как значения коэффициента по всем действиям графика посчитаны, операции, в зависимости от уровня этого параметра, могут быть отнесены к категории:
Оптимизация сетевой модели, нацеленная на сокращение общей продолжительности проекта, как правило, обеспечивается следующими мероприятиями.
Использование табличного метода
Общепризнанные ПП календарного планирования (MS Project, Primavera Suretrack, OpenPlan и т.п.) способны вычислять ключевые параметры сетевой модели проекта. Мы же в настоящем разделе табличным методом выполним настройку подобного расчета обычными средствами MS Excel. Для этого возьмем наш пример фрагмента проектных операций проекта в области СМР. Расположим основные параметры сетевого графика в столбах электронной таблицы.
Преимуществом выполнения расчетов табличным способом является возможность простой автоматизации вычислений и избежание массы ошибок, связанных с человеческим фактором. Красным цветом будем выделять номера операций, располагающихся на критическом пути, а синим цветом отметим расчетные позиции частных резервов, превышающих нулевое значение. Разберем пошагово расчет параметров сетевого графика по основным позициям.
Мы рассмотрели практические механизмы составления сетевого графика и расчета основных параметров временной продолжительности проекта. Таким образом, вплотную приблизились к исследованию возможностей анализа, проводимого с целью оптимизации сетевой модели и формирования непосредственно плана действий по улучшению ее качества. Настоящая тема занимает немного места в комплексе знаний проект-менеджера и не так уж и сложна для восприятия. Во всяком случае, каждый РМ обязан уметь воспроизводить визуализацию графика и выполнять сопутствующие расчеты на хорошем профессиональном уровне.