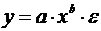рассчитывать параметры парной линейной регрессии можно если у нас есть не менее

Парная регрессия и корреляция

1. Наиболее наглядным видом выбора уравнения парной регрессии является:

в) экспериментальный (табличный).

2. Рассчитывать параметры парной линейной регрессии можно, если у нас есть:

а) не менее 5 наблюдений;

б) не менее 7 наблюдений;

в) не менее 10 наблюдений.

3. Суть метода наименьших квадратов состоит в:

а) минимизации суммы остаточных величин;

б) минимизации дисперсии результативного признака;

в) минимизации суммы квадратов остаточных величин.

4. Коэффициент линейного парного уравнения регрессии:

а) показывает среднее изменение результата с изменением фактора на одну единицу;

б) оценивает статистическую значимость уравнения регрессии;

в) показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%.

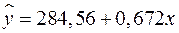
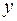
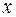
5. На основании наблюдений за 50 семьями построено уравнение регрессии , где – потребление, – доход. Соответствуют ли знаки и значения коэффициентов регрессии теоретическим представлениям?

в) ничего определенного сказать нельзя.

6. Суть коэффициента детерминации 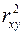состоит в следующем:

а) оценивает качество модели из относительных отклонений по каждому наблюдению;

б) характеризует долю дисперсии результативного признака , объясняемую регрессией, в общей дисперсии результативного признака;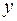

в) характеризует долю дисперсии 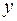, вызванную влиянием не учтенных в модели факторов.

7. Качество модели из относительных отклонений по каждому наблюдению оценивает:

а) коэффициент детерминации ;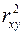

б) 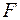-критерий Фишера;

в) средняя ошибка аппроксимации .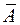

8. Значимость уравнения регрессии в целом оценивает:

а) 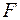-критерий Фишера;

б) 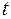-критерий Стьюдента;

в) коэффициент детерминации .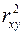

9. Классический метод к оцениванию параметров регрессии основан на:

а) методе наименьших квадратов:

б) методе максимального правдоподобия:

в) шаговом регрессионном анализе.

10. Остаточная сумма квадратов равна нулю:

а) когда правильно подобрана регрессионная модель;

б) когда между признаками существует точная функциональная связь;

11. Объясненная (факторная) сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:

а) ;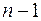

б) ;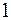

в) .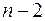

12. Остаточная сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:

а) ;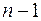

б) ;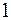

в) .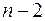

13. Общая сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:

а) ;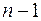

б) ;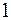

в) .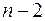

14. Для оценки значимости коэффициентов регрессии рассчитывают:

а) 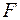-критерий Фишера;

б) 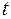-критерий Стьюдента;

в) коэффициент детерминации .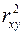

15. Какое уравнение регрессии нельзя свести к линейному виду:

а) ;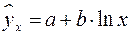

б) :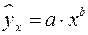

в) .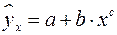

16. Какое из уравнений является степенным:

а) ;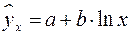

б) :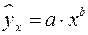

в) .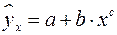

17. Параметр 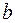в степенной модели является:

а) коэффициентом детерминации;

б) коэффициентом эластичности;

в) коэффициентом корреляции.

18. Коэффициент корреляции 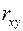может принимать значения:

19. Для функции 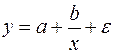средний коэффициент эластичности имеет вид:

а) ;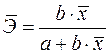

б) ;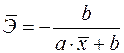

в) .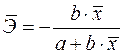

20. Какое из следующих уравнений нелинейно по оцениваемым параметрам:

а) ;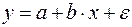

б) ;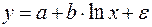

в) .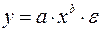

Источник

03. Модель парной линейной регрессии

Методам простой или парной регрессии и корреляции, возможностям их применения в эконометрике посвящен данный раздел.

Любое эконометрическое исследование начинается со Спецификации модели, т. е. с формулировки вида модели исходя из соответствующей теории связи между переменными.

Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной.

Уравнение простой регрессии характеризует связь между двумя переменными, которая проявляется как некоторая закономерность лишь в среднем по совокупности наблюдений. Например, если зависимость спроса у от цены х будет характеризоваться уравнением , то это означает, что с ростом цены на 1 д. е. спрос в среднем уменьшается на 2 д. е. В уравнении регрессии корреляционная по сути связь признаков представляется в виде функциональной связи, выраженной соответствующей математической функцией. Практически в каждом отдельном случае величина у складывается из двух слагаемых:

, (1.1)

Где – фактическое значение результативного признака;

– теоретическое значение результативного признака, найденное исходя из соответствующей математической функции связи у и х, т. е. их уравнения регрессии;

– случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.

Случайная величина ε, или Возмущение, Включает влияние неучтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели обусловлено тремя источниками: спецификацией модели, выборочным характером исходных данных и особенностями измерения переменных.

При правильно выбранной спецификации модели зависит величина случайных ошибок, поэтому, чем они меньше, тем в большей мере теоретические значения результативного признака подходят к фактическим данным .

К ошибкам спецификации будет относится не только неправильный выбор той или иной математической функции для , но и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной.

Наряду с ошибками спецификации могут иметь место ошибки выборки, поскольку исследователь чаще всего работает с выборочными данными при установлении закономерной связи между признаками. Ошибки выборки имеют место и в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении эконометрических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла.

Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки – увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками.

Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели.

В парной регрессии выбор вида математической функции может быть осуществлен тремя методами:

— аналитическим, т. е. исходя из теории изучаемой взаимосвязи;

При изучении зависимости между двумя признаками Графический метод подбора вида уравнения регрессии достаточно нагляден. Он базируется на поле корреляции.

Класс математических функций для описания связи двух переменных достаточно широк. Кроме уже указанных используются и другие типы кривых:

; ; ; ; ; .

Значительный интерес представляет Аналитический метод выбора типа уравнения регрессии. Он основан на изучении материальной природы связи исследуемых признаков.

При обработке информации на компьютере выбор вида уравнения регрессии обычно проводится экспериментальным методом, т. е. путем сравнения величины остаточной дисперсии Dост, рассчитанной при разных моделях.

Если уравнение регрессии проходит через все точки корреляционного поля, что возможно только при функциональной связи, когда все точки лежат на линии регрессии , то фактические значения результативного признака совпадают с теоретическими , т. е. они полностью обусловлены влиянием фактора х. в этом случае остаточная дисперсия Dост=0. В практических исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Оно обусловлено влиянием прочих не учитываемых в уравнении регрессии факторов. Иными словами, имеют место отклонения фактических данных от теоретических (у-). Величина этих отклонений и лежит в основе расчета остаточной дисперсии:

. (1.2)

Чем меньше величина остаточной дисперсии, тем в меньшей мере наблюдается влияние прочих не учитываемых в уравнении регрессии факторов и тем лучше уравнение регрессии подходит к исходным данным.

Линейная регрессия находит широкое применение в эконометрике ввиду четкой экономической интерпретацией ее параметров.

Линейная регрессия сводится к нахождению уравнения вида

или . (1.3)

Построение линейной регрессии сводится к оценке ее параметров – а и b. Классический подход к оцениванию параметров линейной регрессии основан на Методе наименьших квадратов (МНК).

МНК позволяет получить такие оценки параметров а и b, при которых сумма квадратов отклонений фактических значений результативного признака у от расчетных (теоретических) минимальна:

. (1.4)

Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была минимальной.

Для того чтобы найти минимум функции 1.4, надо вычислить частные производные по каждому из параметров а и b и приравнять их к нулю. Обозначим через S, тогда:

;

; (1.5)

.

Преобразуя формулу 1.5, получим следующую систему нормальных уравнений для оценки параметров а и b:

. (1.6)

Решая систему нормальных уравнений 1.6 либо методом последовательного исключения переменных, либо методом определителей, найдем искомые оценки параметров а и b. Можно воспользоваться следующими формулами для а и b:

. (1.7)

Формула 1.7. получена из первого уравнения системы 1.6, если все его члены разделить на n:

,

Где — ковариация признаков;

— дисперсия признака х.

Поскольку , а , получим следующую формулу расчета оценки параметра b:

. (1.8)

Формула 1.8 получается также при решении системы 1.6 методом определителей, если все элементы расчета разделить на n2.

Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Знак при коэффициенте регрессии b показывает направление связи: при b>0 – связь прямая, а при b 0, то относительное изменение результата происходит медленнее, чем изменение фактора.

Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции rxy. Имеются разные модификации формулы линейного коэффициента корреляции, например:

, (1.9)

. (1.10)

Источник

Парная регрессия и корреляция

Парная регрессия и корреляция

1. Наиболее наглядным видом выбора уравнения парной регрессии является:

в) экспериментальный (табличный).

2. Рассчитывать параметры парной линейной регрессии можно, если у нас есть:

а) не менее 5 наблюдений;

б) не менее 7 наблюдений;

в) не менее 10 наблюдений.

3. Суть метода наименьших квадратов состоит в:

а) минимизации суммы остаточных величин;

б) минимизации дисперсии результативного признака;

в) минимизации суммы квадратов остаточных величин.

4. Коэффициент линейного парного уравнения регрессии:

а) показывает среднее изменение результата с изменением фактора на одну единицу;

б) оценивает статистическую значимость уравнения регрессии;

в) показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%.

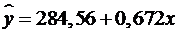
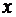
5. На основании наблюдений за 50 семьями построено уравнение регрессии , где – потребление, – доход. Соответствуют ли знаки и значения коэффициентов регрессии теоретическим представлениям?

в) ничего определенного сказать нельзя.

6. Суть коэффициента детерминации 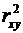состоит в следующем:

а) оценивает качество модели из относительных отклонений по каждому наблюдению;

б) характеризует долю дисперсии результативного признака , объясняемую регрессией, в общей дисперсии результативного признака;

в) характеризует долю дисперсии , вызванную влиянием не учтенных в модели факторов.

7. Качество модели из относительных отклонений по каждому наблюдению оценивает:

а) коэффициент детерминации ;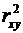

б) 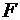-критерий Фишера;

в) средняя ошибка аппроксимации .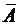

8. Значимость уравнения регрессии в целом оценивает:

а) 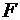-критерий Фишера;

б) 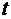-критерий Стьюдента;

в) коэффициент детерминации .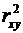

9. Классический метод к оцениванию параметров регрессии основан на:

а) методе наименьших квадратов:

б) методе максимального правдоподобия:

в) шаговом регрессионном анализе.

10. Остаточная сумма квадратов равна нулю:

а) когда правильно подобрана регрессионная модель;

б) когда между признаками существует точная функциональная связь;

11. Объясненная (факторная) сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:

а) ;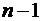

б) ;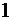

в) .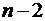

12. Остаточная сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:

а) ;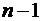

б) ;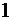

в) .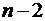

13. Общая сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:

а) ;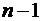

б) ;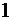

в) .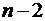

14. Для оценки значимости коэффициентов регрессии рассчитывают:

а) 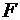-критерий Фишера;

б) 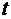-критерий Стьюдента;

в) коэффициент детерминации .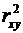

15. Какое уравнение регрессии нельзя свести к линейному виду:

а) ;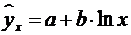

б) :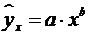

в) .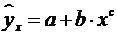

16. Какое из уравнений является степенным:

а) ;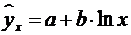

б) :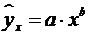

в) .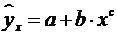

17. Параметр 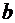в степенной модели является:

а) коэффициентом детерминации;

в) коэффициентом корреляции.

18. Коэффициент корреляции 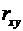может принимать значения:

19. Для функции 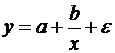средний коэффициент эластичности имеет вид:

а) ;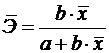

б) ;

в) .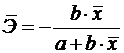

20. Какое из следующих уравнений нелинейно по оцениваемым параметрам:

а) ;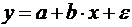

б) ;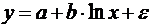

в) .

Источник