равномерная сходимость интеграла с параметром

11.07.202211.07.2022 admin 0 Comments

Равномерная сходимость несобственных интегралов, зависящих от параметра

Считаем, что f непрерывна в этой полосе.

Признак Вейерштрасса равномерной сходимости несобственных интегралов [ править ]

Теорема (Вейерштрасс, Признак равномерной сходимости несобственных интегралов):

Доказательство:

[math]\triangleright[/math]

$ B > A: \left

[math]\triangleleft[/math]

Свойства несобственных интегралов, зависящих от параметра [ править ]

Непрерывность [ править ]

Доказательство ведем по аналогии с рядами.

В силу равномерной сходимости:

$ \forall \varepsilon > 0: \exists A_0: \forall A \ge A_0: \left| \int\limits_A^ <\infty>f(x, y) dx \right| 0: | \Delta y | Повторное интегрирование. [ править ]

Надо установить формулу:

В силу предыдущего параграфа:

Отметим, что интегралы существуют по пункту 1 (непрерывность F по y).

По определению несобственного интеграла, формула верна.

Замечание: можно поставить вопрос:

В ряде частных случаев, ответ будет положительным.

В теории интеграла Лебега будет доказана знаменитая теорема Фубини, полностью решающая этот вопрос, но уже на языке интеграла Лебега.

Формула Лейбница [ править ]

Доказываем по аналогии с функциональными рядами.

Значит, ее можно интегрировать.

По предыдущему пункту, меняем порядок интегрирования.

Бета- и Гамма-функции Эйлера [ править ]

В обоих случаях: интегралы, зависящие от параметра.

Гамма-функция [ править ]

Эта задача решается Гамма-функцией.

Требуется проверить равномерную сходимость интеграла от частной производной.

Аналогично, при двойном дифференцировании получаются равномерно сходящиеся интегралы и т.д.

Можно писать аналогичные формулы, приведенные для Бета-функции, а также связь бета- и гамма-функции с помощью формулы Эйлера:

Источник

Несобственные интегралы, зависящие от параметра. Равномерная сходимость

Равномерная сходимость несобственных интегралов по параметру.

Предположим, что выполнены следующие условия:

Интеграл
$$
\int\limits_<0>^ <+\infty>e^ <-x>\cos xy\ dx\label
$$
сходится равномерно по параметру у на интервале $(-\infty, +\infty) = \mathbb$.

$\vartriangle$ Для любого $\varepsilon > 0$ существует $b’ = \displaystyle\ln \frac<2><\varepsilon>$ такое, что для любого $\xi \in [b’, +\infty)$ и любого $y \in Y$ выполняется неравенство
$$
\left|\int\limits_<\xi>^ <+\infty>e^ <-x>\cos xy\ dx\right| \leq \int\limits_<\xi>^ <+\infty>e^<-x>\ dx = e^ <-\xi>\leq e^ <-b’>= \frac<\varepsilon> <2>Определение.

Интеграл
$$
I_ = \int\limits_<0>^ <+\infty>ye^<-xy>\ dx\nonumber
$$
сходится неравномерно по параметру $y$ на полуинтервале $[0, +\infty)$.

$\vartriangle$ Возьмем $\varepsilon = e^<-1>$. Тогда для любого $b’ \in (0, +\infty)$ существует $\xi = b’$ и $y = 1/b’$ такие, что
$$
\int\limits_<\xi>^ <+\infty>ye^<-xy>\ dx = \int\limits_^ <+\infty>ye^<-xy>\ dx = \int\limits_^ <+\infty>e^<-t>\ dt = \int\limits_<1>^ <+\infty>e^<-t>\ dt = e^ <-1>= \varepsilon,\nonumber
$$
и поэтому интеграл $\displaystyle I_ = \int\limits_<0>^ <+\infty>ye^<-xy>\ dx$ сходится неравномерно по параметру $y$ на множестве $Y = [0, +\infty)$. $\blacktriangle$

Признаки равномерной сходимости несобственных интегралов по параметру.

(Признак Вейерштрасса равномерной сходимости несобственного интеграла по параметру).

Пусть для любого $y \in Y$ функция $f(x, y)$ интегрируема по $x$ на любом отрезке $[a, b’] \subset [a, b)$, и пусть на $[a, b)$ существует функция $\varphi(x)$ такая, что для всех $y \in Y$ и всех $x \in [a, b)$ выполнено неравенство $|f(x, y)| \leq \varphi(x)$, а несобственный интеграл $\displaystyle\int\limits_^ \varphi(x)\ dx$ сходится.

Интеграл
$$
\int\limits_<0>^ <+\infty>\frac<\cos xy><1+x^<2>>\ dx\label
$$
сходится равномерно по параметру $y$ на интервале $(-\infty, +\infty)$.

$\vartriangle$ Так как $\displaystyle\frac<|\cos xy|><1+x^<2>> \leq \frac<1><1+x^<2>>$ и $\displaystyle\int\limits_<0>^ <+\infty>\frac<1+x^<2>> = \frac<\pi><2>$, то по признаку Вейерштрасса интеграл \eqref сходится равномерно по параметру $y$ на $(-\infty, +\infty)$. $\blacktriangle$

Докажем признак Дирихле равномерной сходимости для интегралов вида
$$
\int\limits_^ <+\infty>f(x, y) g(x, y)\ dx,\ y \in Y.\label
$$

(Признак Дирихле равномерной сходимости несобственного интеграла по параметру).

Тогда интеграл \eqref сходится равномерно по параметру $y$ на множестве $Y$.

$\circ$ По признаку Дирихле несобственный интеграл \eqref сходится при любом $y \in Y$. Покажем, что он сходится равномерно по параметру $y$ на множестве $Y$.

Так как по условию 4) функция $\psi(x) \rightarrow 0$ при $x \rightarrow +\infty$, то для любого $\varepsilon > 0$ существует $a’ > a$ такое, что для любого $\xi \in [a’, +\infty)$ выполнено неравенство
$$
\psi(\xi) Замечание 2.

Если $+\infty$ — единственная особая точка сходящегося интеграла \eqref, то этот интеграл сходится равномерно по параметру $y$ на множестве $Y$ в том и только том случае, когда при любом $a’ > a$ интеграл $\displaystyle\int\limits_^ <+\infty>f(x, y) g(x, y)\ dx$ сходится равномерно по параметру $y$ на множестве $Y$.

Поэтому для справедливости утверждения теоремы 2 достаточно, чтобы условия 1)-4) выполнялись на некотором промежутке $[a’, +\infty) \subset [a, +\infty)$.

Интеграл
$$
\int\limits_<0>^ <+\infty>e^ <-xy>\frac<\sin x>\ dx\label
$$
сходится равномерно по параметру $y$ при $y \in [0, +\infty)$.

$\vartriangle$ Так как функция $\sin x$ имеет ограниченную первообразную, а при $x \geq 1$, $y \geq 0$ выполнены следующие условия:
$$
\frac<\partial> <\partial x>\left(\frac>\right) =-\frac>>(1+xy) Теорема 3.

(Критерий Коши равномерной сходимости несобственного интеграла по параметру).

Получаем, что для любого $\xi \in [b’, b)$ и для любого $y \in Y$ выполнено неравенство $\displaystyle\left|\int\limits_<\xi>^ f(x, y)\ dx\right| \leq \varepsilon$, из которого следует, что интеграл $\int\limits_^ f(x, y)\ dx$ сходится равномерно по параметру $y$ на множестве $Y$. $\bullet$

Применяя правило построения отрицания, получаем из критерия Коши полезное следствие.

Если существует $\varepsilon_ <0>> 0$ такое, что для любого $b’ \in [a, b)$ существуют $\xi_<0>, \xi’_ <0>\in [b’, b)$ и существует $y_ <0>\in Y$ такие, что
$$
\left|\int\limits_<\xi_<0>>^<\xi’_<0>> f(x, y_<0>)\ dx\right| \geq \varepsilon_<0>,
$$
то интеграл $\displaystyle\int\limits_^ f(x, y)\ dx$ не сходится равномерно по параметру $y$ на множестве $Y$.

Интеграл
$$
\int\limits_<0>^ <+\infty>e^<-\alpha x^<2>>\ dx\label
$$
сходится равномерно по параметру $\alpha$ на множестве $[\alpha_<0>, +\infty)$, $\alpha_ <0>> 0$, и сходится неравномерно на множестве $(0, +\infty)$.

$\vartriangle$ Пусть $\alpha \geq \alpha_ <0>> 0$. Так как $e^<-\alpha x^<2>> \leq e^ <-\alpha_<0>x^<2>>$ и $\displaystyle\int\limits_<0>^ <+\infty>e^<-\alpha x^<2>>\ dx$ сходится, то по признаку Вейерштрасса интеграл \eqref сходится равномерно по параметру $\alpha$ на множестве $[\alpha_<0>, +\infty)$.

Пусть теперь $\alpha \in (0, +\infty)$. Покажем, что на $(0, +\infty)$ интеграл \eqref сходится неравномерно. Воспользуемся следствием из критерия Коши. Возьмем $\varepsilon_ <0>= e^<-1>$, для любого $b > 0$ возьмем $\xi_ <0>= b$, $\xi’_ <0>= b+1$, $\alpha_ <0>= 1/(b+1)^<2>$. Тогда
$$
\int\limits_<\xi_<0>>^<\xi’_<0>> e^ <-\alpha_<0>x^<2>>\ dx = \int\limits_^ e^ <-\alpha_<0>x^<2>>\ dx \geq e^ <-\alpha_<0>(b+1)^<2>> \int\limits_^ dx = e^ <-1>= \varepsilon_<0>\nonumber
$$
и, следовательно, интеграл \eqref сходится неравномерно по параметру $\alpha$ на множестве $(0, +\infty)$. $\blacktriangle$

Непрерывность, интегрируемость и дифференцируемость несобственного интеграла по параметру.

$\vartriangle$ Если функцию $\displaystyle\frac<\sin x>$ доопределить при $x = 0$ по непрерывности, считая, что при $x = 0$ функция $\frac<\sin x>$ принимает значение, равное единице, то подынтегральная функция интеграла \eqref будет непрерывной на множестве $\<(x, y): x \geq 0, y \geq 0\>$.

При рассмотрении примера 4 было показано, что интеграл \eqref сходится равномерно по параметру $y$ на множестве $[0, +\infty)$. В силу теоремы 4 интеграл \eqref есть непрерывная функция параметра $y$ на любом отрезке $[0, b]$. В частности, эта функция непрерывна при $y = 0$, поэтому должно быть выполнено равенство \eqref. $\blacktriangle$

(Теорема о перестановке порядка интегрирования).

$\vartriangle$ Воспользуемся известной формулой
$$
\int\limits_<0>^ <+\infty>e^ <-xy>\sin x\ dx = \frac<1><1+y^<2>>,\ y > 0.\label
$$

Интеграл \eqref сходится равномерно по параметру $y$ на любом отрезке $[\delta, N]$, где $\delta > 0$. Это следует из признака Вейерштрасса равномерной сходимости, так как
$$
|e^ <-xy>\sin x\ dx| \leq e^<-\delta x>,\quad \int\limits_<0>^ <+\infty>e^<-\delta x>\ dx = \frac<1><\delta>.\nonumber
$$
Применяя теорему 5 и интегрируя равенство \eqref, получаем
$$
\operatorname N-\operatorname \delta = \int\limits_<0>^<+\infty>\ dx \int\limits_<\delta>^ e^ <-xy>\sin x\ dy = \int\limits_<0>^ <+\infty>\dfrac-e^<-Nx>> \sin x\ dx.\label
$$

Так как $|\sin x| \leq x$ при $x \geq 0$, то
$$
\left|\int\limits_<0>^ <+\infty>\dfrac\sin x>\ dx\right| \leq \int\limits_<0>^ <+\infty>e^<-Nx>\ dx = \frac<1>.\nonumber
$$
Переходя к пределу при $N \rightarrow +\infty$ в равенстве \eqref, получаем
$$
\frac<\pi><2>-\operatorname \delta = \int\limits_<0>^ <+\infty>e^ <-\delta x>\frac<\sin x>\ dx.
$$
Воспользовавшись равенством \eqref и переходя к пределу при $\delta \rightarrow +0$, получаем выражение \eqref для интеграла Дирихле. $\blacktriangle$

(Теорема о дифференцировании несобственного интеграла по параметру).

Пусть функции $f(x, y)$ и $f_(x, y)$ непрерывны на множестве \(\<(x, y):\ a\leq x Доказательство.

$\circ$ Пусть $c \leq y \leq d$. Рассмотрим интеграл $\displaystyle\int\limits_^ f_(x, \eta)\ dx$ при $\eta \in [c, y]$.

Покажем, что $C_ <2>= 0$. Так как
$$
|I_<1>(y)| = \left|\int\limits_<0>^ <+\infty>\frac<\cos xy><1+x^<2>>\ dx\right| \leq \int\limits_<0>^ <+\infty>\frac<|\cos xy|><1+x^<2>>\ dx \leq \int\limits_<0>^ <+\infty>\frac<1+x^<2>> = \frac<\pi><2>,\nonumber
$$
то $I_<1>(y)$ есть ограниченная функция на $[\delta, +\infty)$. Так как $e^$ — неограниченная функция на $[\delta, +\infty)$, то в формуле \eqref нужно принять $C_ <2>= 0$.

Замечая, что интеграл Лапласа $I_<1>(y)$ есть четная функция на $(-\infty, +\infty)$, а интеграл $I_<2>(y)$ есть нечетная функция на $(-\infty, +\infty)$, перепишем равенство \eqref в следующем виде:
$$
I_<1>(y) = C_<1>e^<-|y|>,\ I_<2>(y) = C_<1>\ \operatorname\ ye^<-|y|>\ \mbox<при>\ y \neq 0.\label
$$

Для определения произвольной постоянной $C_<1>$ воспользуемся тем, что интеграл Лапласа $I_<1>(y)$ сходится равномерно по параметру $y$ на $(-\infty, +\infty)$ (пример 3). Поэтому $I_<1>(y)$ есть непрерывная функция в точке $y = 0$. Следовательно,
$$
\frac<\pi> <2>= \int\limits_<0>^ <+\infty>\frac<1+x^<2>> = I_<1>(0) = \lim_ I_<1>(y) = \lim_ C_<1>e^ <-y>= C_<1>.\nonumber
$$
Теперь формулы \eqref дают, что при любом $y \in \boldsymbol$
$$
\int\limits_<0>^ <+\infty>\frac<\cos xy><1+x^<2>>\ dx = \frac<\pi><2>e^<-|y|>,\\ \int\limits_<0>^ <+\infty>\frac<1+x^<2>>\ dx = \frac<\pi><2>\ \operatorname\ ye^<-|y|>.\label
$$
То, что формулы \eqref справедливы при $y = 0$, проверяется непосредственно. $\blacktriangle$

Перестановка порядка интегрирования в том случае, когда оба интеграла несобственные.

В теореме 5 была обоснована перестановка порядка интегрирования, когда внутренний интеграл несобственный, а внешний собственный. Сложнее обосновывать перестановку порядка интегрирования, когда оба интеграла несобственные.

Пусть функция $f(x, y)$ непрерывна на множестве $\<(x, y): a \leq x \leq b,\ c \leq y \leq d\>$ и выполнены следующие условия:

Теоремы 4-7 остаются справедливыми и при замене функции $f(x, y)$ на функцию $\psi(x)f(x, y)$, где функция $\psi(x)$ интегрируема по Риману на любом отрезке, лежащем в интервале $(a, b)$.

Если $f(x, y) = \varphi(x, y)+i\psi(x, y)$ есть комплекснозначная функция, то
$$
|\varphi(x, y)| \leq |f(x, y)|,\ |\psi(x, y)| \leq |f(x, y)|.\nonumber
$$

Все условия теоремы будут выполнены и для функций $\varphi(x, y)$ и $\psi(x, y)$, если $f(x, y)$ удовлетворяет условиям теоремы 7. Поэтому оба повторных интеграла от каждой из этих функций существуют и равны. Следовательно, существуют и равны повторные интегралы от функции $f(x, y)$.

Вычислить интеграл Эйлера-Пуассона (интеграл вероятностей)
$$
I = \int\limits_<0>^ <+\infty>e^<-t^<2>> dt.\nonumber
$$

Для обоснования законности изменения порядка интегрирования применим теорему 7. Интеграл $\displaystyle\int\limits_<0>^ <+\infty>ye^<-y^<2>(1+x^<2>)> dx$ сходится равномерно по параметру $y$ на любом отрезке $[c, d] \subset (0, +\infty)$ по признаку Вейерштрасса, так как $|ye^<-y^<2>(1+x^<2>)>| \leq de^<-c^<2>(1+x^<2>)>$ а интеграл $\displaystyle\int\limits_<0>^ <+\infty>de^<-c^<2>(1+x^<2>)> dx$ сходится.

Аналогично доказывается, что интеграл $\displaystyle\int\limits_<0>^ <+\infty>ye^<-y^<2>(1+x^<2>)> dx$ сходится равномерно по параметру $x$ на любом отрезке $[a, b] \subset (0, +\infty)$. Повторный интеграл $\int\limits_<0>^ <+\infty>ye^<-y^<2>(1+x^<2>)> dx$ сходится в силу равенства \eqref.

Вычислить интегралы Френеля
$$
J_ <1>= \int\limits_<0>^ <+\infty>\sin x^<2>\ dx,\ J_ <2>= \int\limits_<0>^ <+\infty>\cos x^<2>\ dx.
$$

При написании формул \eqref использована равномерная сходимость несобственных интегралов в правых частях равенств \eqref по параметру $k$ при $k \geq 0$ (признак Дирихле).

Изменение порядка интегрирования при $k > 0$ обосновывается при помощи теоремы 7, предельный переход при $k \rightarrow +0$ под знаком интеграла возможен в силу его равномерной сходимости по параметру $k$ при $k \in [0, +\infty)$ (признак Вейерштрасса). Интегралы $\displaystyle\int\limits_<0>^ <+\infty>\frac<1+x^<4>>$ и $\displaystyle\int\limits_<0>^ <+\infty>\fracdx><1+x^<4>>$ вычислены нами ранее (примеры здесь и здесь). $\blacktriangle$

Источник

Интегралы, зависящие от параметра

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

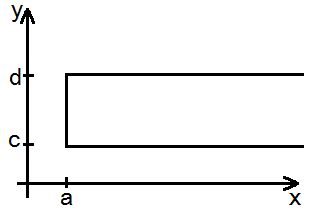
Собственные интегралы, зависящие от параметра 1.1. Понятие интеграла, зависящего от параметра, и его непрерывность Пусть в прямоугольнике определена функция двух переменных f(x, у) (рис. 1). Предположим, что при любом фиксированном значении у е [с, d] существует интеграл ь Ясно, что этот интеграл является функцией переменного у, Интеграл (1) называется интегралом, зависящим от параметра у. Имеет место следующая теорема о непрерывности интеграла, зависящего от параметра.

Теорема 1:

Если функция /(х, у) непрерывна в прямоугольнике П, то функция /(у), определенная соотношением (1), непрерывна на отрезке [с, d\. Из формулы (1) вытекает, что приращение ) функции /(у), соответствующее приращению аргумента Ду, можно оценить так: По условию теоремы функция f у) непрерывна в замкнутом прямоугольнике П, а значит, fy) равномерно непрерывна в этом прямоугольнике.

Возможно вам будут полезны данные страницы:

Интеграл (1) называется абсолютно сходящимся на отрезке [с, d\, если сходится интеграл Собственные интегралы зависящие от параметра Дифференцирование интеграла no параметру Интегрирование интеграла по параметру Понятие несобственного интеграла первого рода, зависящего от параметра Равномерная сходимость несобственного интеграла Критерий Коши Свойства равномерно сходящихся несобственных интегралов, зависящих от параметра 2.2. Равномерная сходимость несобственного интеграла. Критерий Коши Определение 2.

Несобственный интеграл

Несобственный интеграл (1) называется равномерно сходящимся по параметру у наотрезке [с, d), если он сходится наэтомотрезкеи для любого е > 0 можно указать такое А ^ а, зависящее только от е, что для всех В > А и для всех у из отрезка [с, d\ выполняется неравенство Имеетместоследующий критерий Коши равномерной сходимости несобстве нных интегралов, зависящих от параметра.

Теорема 4. Для того, чтобы несобственный интеграл (1) равномерно сходился по параметру у на отрезке [с, d\, необходимо и достаточно, чтобы для любого е > 0 можно было указать число А ^ а, зависящее только от е и такое, что для любых В и С, больших А, и для всех у из отрезка [с, d] выполнялось неравенство Справедливость этого критерия вытекает непосредственно из определения равномерной сходимости. Сформулируем достаточный признак равномерной сходимости несобственных интегралов, зависящих от параметра. Теорема 5 (признак Вейерштрасса).

Пусть функция /(х, у) определена в пыупыосе Поо и для каждого у € | с, d] интегрируема по х на любом отрезке [а, Л]. Пусть, кроме того, для всех точек полуполосы П^ выполняется неравенство Тогда из сходимости интеграла f g(x) dx вытекает равномерная сходимость по у наот- резке [с, d] несобственного интегрша В силу критерия Коши сходимости интеграла от функции для любого е > О можно указать число А ^ а такое, что при всех С > В ^ А выполняется неравенство Используя неравенство (4), отсюда получим, что для всех у из отрезка Тем самым, критерий Коши равномерной сходимости интеграла выполнен. Цитр 1.

Иссладова тъ на равномерную сходимость несобственный иктграл где я — параметр, Так как при любом произвольные вещественные числа, выполняется неравенство и интеграл сходится, то по признаку Вейерштрасса интеграл (5) равномерно сходится для всех 2.3. Свойства равномерно сходящихся несобственных интегралов, зависящих от параметра Свойство 1. Непрерывность несобственного интеграла по параметру. Если функция непрерывна в области Поо и интеграл сходится равномернопо у наотрезкс (с, dj,то функция 1(у) непрерывна на Свойство 2. Интегрируемость несобственно го интеграла по параметру.

В самом деле, при любом в, и откуда по признаку Вейерштрасса следует равномерная сходимость интеграла (9). Обозначая подынтегральную функцию интеграла (5) через замечаем, что — подынтегральная функция равномерно сходящегося интеграла (9). Используя свойство дифференцируемое™ несобственного интеграла по параметру, получим Так как 1($) = (в этом легко убедиться путем интегрирования по частям), то Отсюда Пример 3.

Покажем сначала, что несобственный интеграл Собственные интегралы зависящие от параметра Дифференцирование интеграла no параметру Интегрирование интеграла по параметру Понятие несобственного интеграла первого рода, зависящего от параметра Равномерная сходимость несобственного интеграла Критерий Коши Свойства равномерно сходящихся несобственных интегралов, зависящих от параметра зависящий от параметра у, сходится равномерно на отрезке (а, 6).

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Интегралы, зависящие от параметра. Несобственные интегралы с параметром

Страницы работы

Содержание работы

16 Интегралы, зависящие от параметра

Пусть f(x,y) – функция двух переменных, определённая на прямоугольнике

Если для любого yÎ[c, d] существует интеграл 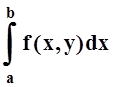, то этот интеграл является функцией от переменной y (которая и называется здесь параметром):

Таким образом, мы получаем новый способ задания функции – в виде интеграла, зависящего от параметра.

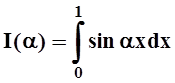
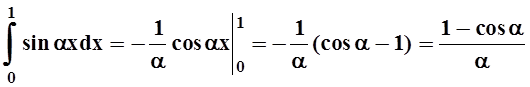
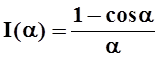
Пример 1. Рассмотрим функцию . В этом примере интеграл легко вычислить: . Значит, I(a) можно задать и обычным способом: .

Однако часто встречаются интегралы, которые не выражаются через элементарные функции. Тогда приходится работать с функцией, заданной в виде интеграла с параметром. Значит, нужно научиться работать с такими функциями – в частности, знать правила их дифференцирования и интегрирования.

Возможна и более сложная ситуация, когда от параметра зависит не только подинтегральная функция, но и пределы интегрирования: .

16.1 Основные теоремы

16.1.1 Предельный переход под знаком интеграла.

Теорема 1 (о непрерывности интеграла с параметром). Если функция f(x,y) непрерывна на прямоугольнике D= [a, b] ´ [c, d], то функция 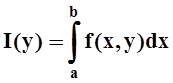непрерывна на отрезке [c, d].

Доказательство. По теореме Кантора, непрерывная на компактном множестве Dфункция является равномерно непрерывной, т.е.

Источник

Равномерная сходимость интеграла с параметром

Если подынтегральная функция несобственного интеграла зависит от параметра то числа о которых говорилось в общих признаках 1 и 2 из [85], вообще говоря, зависят от у. Если при изменении у в промежутке числа и N в условиях

можно выбрать независимо от значений у, то несобственные интегралы

называются равномерно сходящимися относительно у.

В частности, интегралы, которые встречаются при применении признаков Коши, будут равномерно сходящимися, постоянные не зависят от у.

Всякий сходящийся несобственный интеграл мы можем представить в виде сходящегося ряда, каждый член которого есть уже обычный интеграл. Этим приемом мы уже пользовались в предыдущем. Обратимся к первому из интегралов (43). Задав ряд положительных, убывающих и стремящихся к нулю чисел

В случае второго из интегралов (43), задав ряд беспредельно возрастающих чисел

Из определения равномерной сходимости интеграла и ряда [I, 143] непосредственно вытекает, что если несобственный интеграл сходится равномерно, то и соответствующий ему ряд будет равномерно сходящимся при любом выборе чисел (44) или (47). Действительно, например, сумма далеких членов ряда (45) равна интегралу по отрезку, близкому к b, для которого соблюдено неравенство (41).

Свойства равномерно сходящихся интегралов аналогичны свойствам равномерно сходящихся рядов [I, 146]. Для определенности формулируем их для второго из интегралов (43), но сказанное применимо и для первого.

1) Если функция f(x, у) непрерывна при и при изменении у в некотором конечном промежутке и интеграл

равномерно сходится, то он есть непрерывная функция от у при

2) При тех же условиях имеет место и формула интегрирования под знаком интеграла:

3) Если при непрерывности интеграл (49) сходится, а интеграл

сходится равномерно, то имеет место формула дифференцирования под знаком интеграла:

Докажем для примера свойства 1) и 3). Члены ряда (48)

по доказанному в [83], суть непрерывные функции, и, в силу равномерной сходимости интеграла, этот ряд сходится равномерно, и, следовательно, сумма ряда, т. е. интеграл (49), тоже есть непрерывная функция [I, 146].

Для доказательства (3) заметим, что из [83] следует, что интегралы (53) можно дифференцировать под знаком интеграла, т. е.

Но, в силу равномерной сходимости интеграла (51), мы имеем равномерно сходящийся ряд

Игпк, ряд (48) сходится, а ряд из производных сходится равномерно. Отсюда следует [I, 146), что сумма ряда (54) есть производная от суммы ряда (48), что и приводит к формуле (52).

Укажем простой признак абсолютной и равномерной сходимости несобственного интеграла, аналогичный признаку абсолютной и равномерной сходимости ряда . Сделаем это для второго из интегралов . Аналогичный признак имеет место и для первого интеграла.