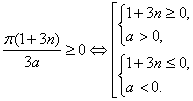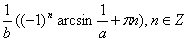решить тригонометрическое неравенство с параметром

Тригонометрические уравнения и неравенства с параметрами: формулы, примеры

Содержание:

Тригонометрический пример с неизвестным – уравнение. Теория относит к данной классификации выражения, в которых искомый коэффициент располагается исключительно под знаком тригонометрического функционала. Алгебра предлагает два варианта решения задачи:

С помощью окружности можно измерить угол, определить значение косинуса, синуса, тангенса или котангенса. Чтобы решать тригонометрические уравнения с параметром, необходимо привести выражение к простейшей форме. Важно учитывать допустимый диапазон и ограничения функционала: у = cosx; x = sinx.

Тригонометрические функции с параметрами – когда нужна проверка

Математика – сложный предмет, где после получения решения зачастую необходимо проверять его достоверность. Уравнение необходимо проверить, чтобы убедиться в правильности найденных корней. Анализ проводится в следующих случаях:

Тригонометрические уравнения и неравенства с параметрами – пример

(tgp — 6) 2 — (α 2 — 4α + 10) * ((tgp — 6) — 4α 3 + 10α 2 = 0

Переменная р предусматривает наличие 120 вариантов решения. Установлен полуинтервал: [0, 60π].

Исходя из условия, можно отметить наличие 4 решений для каждого оборота. Допускается пара вариантов функции tg. Необходимое требование для данного задания – положительное значение дискриминанта. Это единственный вариант получения двух корней в квадратном уравнении. Вводим систему:

D = (α 2 — 4α + 10) 2 — 4 * (10α 2 — 4α 3 )
D = (α 2 + (10 — 4α)) 2 — 4α 2 (10 — 4α)
D = α 4 — 2α 2 (10 — 4α + (10 — 4α 2 ) = (α 2 + 4α — 10) 2

Тригонометрия с параметром – решение сложного уравнения

В задании представлено сложное выражение функции с параметрами. При этом для обозначения неизвестного используется Х, параметр обозначен А. Общий вид примера:

2 * sin 2 x + sin x sin x = A

Для решения необходимо трактовать формулу как пример квадратного уравнения по sin sin x. Требуется введение дополнительного коэффициента [t], меньшего или равного единице. Допускается создание вспомогательного примера с дискриминантом D = 1 + 8α

При 1+8α меньше нуля у вспомогательного и исходного задания отсутствуют решения.

x = (-1)^ \arcsin \frac <1> <4>+ \pi n, n \in Z.

2 — 1 — А ≥ 0,2 + 1 — А ≥ 0.

Источник

Тригонометрические неравенства с параметром

п.1. Примеры

Пример 1. Решите неравенства:

a) \(sinax\gt\frac12\) \begin \frac\pi6+2\pi k\lt ax\lt\frac<5\pi><6>+2\pi k \end При \(a=0\) решений нет. При \(a\lt 0:\ \frac<\pi><6a>+\frac<2\pi k>\gt x\gt \frac<5\pi><6a>+\frac<2\pi k>\) При \(a\gt 0:\ \frac<\pi><6a>+\frac<2\pi k>\lt x\lt \frac<5\pi><6a>+\frac<2\pi k>\)

Пример 2. Найдите \(a\), при которых неравенство выполняются для любых \(x\in\mathbb\):

a) \((a^2-4)cosx+4asinx\leq 5a\)
Введем вспомогательный угол: \begin \rho=\sqrt<(a^2-4)^2+(4a)^2>=\sqrt=\sqrt=\\ =\sqrt<(a^2+4)^2>=|a^2+4|=a^2+4\gt 0 \end Разделим на \(\rho:\) \begin \frac<(a^2-4)>cosx+\frac<4a>sinx\leq\frac<5a>\\ cos\varphi=\frac<(a^2-4)>,\ \ sin\varphi=\frac<4a>\\ cos\varphi cosx+sin\varphi sinx\leq\frac<5a>\\ cos(x-\varphi)\leq\frac<5a>\\ cox(x-\varphi)\leq 1\leq \frac<5a> \end Неравенство выполняется при любых \(x\), если: \begin \frac<5a>\geq 1\Rightarrow 5a\geq a^2+4\Rightarrow a^2-5a+4\leq 0\Rightarrow (a-1)(a-4)\leq 0\Rightarrow\\ \Rightarrow 1\leq a\leq 4 \end Ответ: \(a\in[1;4]\)

б) \(sin^2x+a(2-cosx)^2-7+7a\gt 0\)
Решим неравенство относительно a: \begin a((2-cosx)^2+7)\gt 7-sin^2x\\ a\gt\frac<7-sin^2x> <(2-cosx)^2+7>\end Чтобы неравенство выполнялось для любого \(x\), нужно найти максимум функции справа. Дробь будет максимальной при наибольшем числителе и наименьшем знаменателе: \begin f(x)=\frac<7-sin^2x><(2-cosx)^2+7>,\ \ f_=\frac<7-0><(2-1)^2+7>=\frac78,\ x=\pi k \end Откуда: \(a\gt\frac78\)
Ответ: \(a\in\left(\frac78;+\infty\right)\)

Пример 3. Найдите \(a\), при которых система имеет единственное решение:
a) \begin \begin (tgx-1)(x+a)=0\\ |x|\lt 1 \end \end Решаем уравнение: \begin (tgx-1)(x+a)=0\Rightarrow \left[ \begin tgx=1\\ x=-a \end \right. \Rightarrow \left[ \begin x=\frac\pi4+\pi k\\ x=-a \end \right. \end Пусть единственным решением будет \(x=\frac\pi4+\pi k\). Тогда, учитывая \(|x|\lt 1\), исключаем второе решение: \begin \begin x=\frac\pi4+\pi k\\ |x|\lt 1\\ |-a|\geq 1 \end \Rightarrow \begin x=\frac\pi4\\ |a|\geq 1 \end \end Также, решения совпадают, если: \begin a=-\frac\pi4:\ \begin tgx=1\\ x=\frac\pi4\\ |x|\gt 1 \end \Rightarrow x=\frac\pi4 \end При других \(a\) решений будет два.
Ответ: \(a\in\left.\left(-\infty;-1\right.\right]\cup \left\<\frac\pi4\right\>\cup\left.\left[1;+\infty\right.\right),\) единственное решение \(x=\frac\pi4\)

При \(a=-\frac13\) вершина \(x_0=\frac13.\) Единственное решение \(\left(\frac13,\ \pi-arccos\frac35\right)\)

При \(a=2\) вершина \(x_0=-2.\) Единственное решение \(\left(-2,\ \pi-arccos\frac35\right)\)

При других значениях \(a\) парабола либо поднимается выше уровня 5, и тогда система не имеет решений; либо опускается ниже уровня 5, и тогда система имеет бесконечное множество решений.

Ответ: \(a=-\frac13\), единственное решение \(\left(\frac13,\ \pi-arccos\frac35\right)\)
\(a=2\), eдинственное решение \(\left(-2,\ \pi-arccos\frac35\right)\)

Источник

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №48. Тригонометрические уравнения с параметром.

Перечень вопросов, рассматриваемых в теме:

1) Тригонометрическое уравнение с параметром;

2) Решение тригонометрического уравнения с параметром;

3) Значения параметра, при котором простейшее тригонометрическое неравенство имеет решение.

Если некоторое уравнение F(x, a)=0 требуется решить относительно переменной х, то а называется параметром, а это уравнение называется уравнением с параметром а относительно переменной х.

Амелькин,, В.В., Рабцевич В.Л., Задачи с параметрами: Справ. пособие по математике – М.: «Асар», 1996. – 464 с.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

1. Если некоторое уравнение F(x, a)=0 требуется решить относительно переменной х, то а называется параметром, то это уравнение называется уравнением с параметром а относительно переменной икс.

Простейшим примером уравнения с параметром является такое: .

Если требуется решить такое уравнение, то ответ мы должны записать так:

1) при |a|>1 уравнение решений не имеет

3) при 0 1 уравнение решений не имеет

2) при

).

2. Рассмотрим решение более сложных тригонометрических уравнений с параметрами.

Решите уравнение с переменной х и параметром а:

Его дискриминант:

Очевидно, что если , то есть , то вспомогательное уравнение и исходное уравнение решений не имеют.

Если , то вспомогательное уравнение имеет один корень: . Это удовлетворяет условию , поэтому при .

.

Если , то вспомогательное уравнение имеет два корня. Но для того чтобы исходное уравнение имело корни, нужно чтобы .

Так как вершина параболы находится в точке , то для того чтобы вспомогательное уравнение имело на отрезке [-1; 1] одно решение, нужно, чтобы выполнялось условие: ,

где .

То есть одно решение на отрезке [-1; 1] вспомогательное уравнение будет иметь при , причем это больший корень вспомогательного уравнения:

, , .

два решения на отрезке [-1; 1] вспомогательное уравнение будет иметь при

.

.

2) при .

3) при .

4) при .

Если в этом примере требуется найти наибольшее значение параметра, при котором уравнение имеет решение, то ответ будет 3. Если требуется найти, например, наименьшее целое решение, то ответ будет 0.

Решим относительно переменной x уравнение:

Преобразуем исходное уравнение:

Рассмотрим полученное уравнение как квадратное относительно . Введем новую переменную .

Рассмотрим вспомогательное уравнение.

.

Его дискриминант:

Видно, что это уравнение имеет решение только при a=0. При остальных значениях параметра уравнение решений не имеет.

Проверим, дает ли полученное решение вспомогательного уравнения решение исходного уравнения.

Если a=0,то .

Отсюда .

Ответ: 1) при ,

2) при решений нет.

Примеры и разбор решения заданий тренировочного модуля

1. При каком наибольшем значении параметра уравнение имеет решение

Найдем его дискриминант:

Видно, что вспомогательное уравнение всегда имеет решение.

Но , поэтому нужно выяснить, при каком значении параметра t корни уравнения попадают в отрезок [0; 1].

Так как старший коэффициент этого уравнения положителен, то для того чтобы хотя бы один корень уравнения (функции f(p)) попал в отрезок [0; 1], нужно, чтобы выполнялось одно из неравенств: .

, . Наибольшее значение 0.

2. Найдите наименьшее положительно значение параметра, при котором решением неравенства является любое действительное число.

Неравенство всегда верно, то есть выполнено при любых значениях переменной. Значит, данное неравенство будет всегда верно, если , то есть , .

Наименьшее положительное значение параметра .

Источник

Решить тригонометрическое неравенство с параметром

Решение: Так как Е(со s t )=[-1; 1], то имеем два случая.

1. При |a| > 0,5 уравнение не имеет решений.

Ответ: если |a| > 0,5, решений нет;

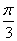
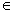
ах 2 = +π n , n Z

Если коэффициент при неизвестном зависит от параметра, то появляется особое значение параметра. В данном случае:

1. Если а=0, то уравнение не имеет решений.

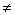
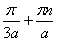
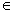
2. Если а 0, то х 2 = , n Z

Уравнение имеет решение, если 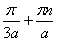≥ 0. Выясним, при каких значениях n

и а выполняется это условие:

≥ 0

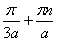
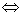
2) а и n 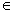Z .

Ответ: при а = 0 решений нет;

Пример. Решите уравнение: а sin bx = 1

Решение: Особое значение параметра а : а = 0.

1. При а = 0 решений нет.

2.1. Если 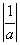> 1, то решений нет.

2.2. Если ≤ 1, то особое значение b = 0:

2.2.1. Если b = 0, то решений нет.

2.2.2. Если b 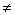0, то х =

Ответ: при а = 0 или > 1 и а 0 или а 0 b = 0 решений нет;

Источник