рівняння з параметрами це

11.07.202211.07.2022 admin 0 Comments

Рівняння з параметрами це

Тема: «Квадратні рівняння та задачі з параметрами»

1. Суть рівнянь з параметром

2. Приклади розв’язання рівнянь та задач

3. Завдання для самостійного опрацювання

1. Суть рівнянь з параметром

1)розв’язати задане рівняння чи нерівність;

2)дослідити одержаний розв’язок.

2.Приклади розв’язання рівнянь та задач.

Розв’яжіть рівняння: х 2 – 5х + а = 0

D = (– 5) 2 – 4а = 25 – 4а

3)Якщо D 6,25, то рівняння не має коренів.

Розв’яжіть рівняння: х 2 + bx + 4 = 0

Розв’яжіть рівняння: ах 2 + 6х + 1 = 0.

3)Якщо D ¹ 0, то рівняння не має коренів.

Розв’яжіть рівняння та дослідіть одержаний розв’язок: 2а(а – 2)х = а – 2

Дослідження та розв’язання.

Якщо а = 0, то рівняння має вигляд 0х = – 2. Рівняння не має коренів. Якщо а = 2, то рівняння має вигляд 0х = 0. Рівняння має безліч коренів.

Відповідь: Якщо а = 0, то рівняння не має коренів.

Якщо а = 2, то рівняння має безліч коренів.

Розв’яжіть рівняння: (а – 1) х 2 + 2(2а + 1) х + 4а + 3 = 0

Виділимо особливі значення параметра а.

Якщо а ¹ 1, то виділимо ті значення параметра, при яких дискримінант квадратного рівняння дорівнює нулю.

Маємо = 5а + 4. Значить, а = – значення параметра, на яке необхідно звернути увагу.

Якщо а > – і а ¹ 1 то D > 0 і ми отримаємо:

При яких значеннях параметра а рівняння х 2 + 2(а + 1) х + 9а – 5 = 0 має два різні від’ємні корені.

Так як рівняння повинно мати два різні корені х₁ і х₂, то його дискримінант повинен бути додатнім.

Маємо: D =4(а + 1) 2 – 4(9а – 5) = 4а 2 – 28 + 24 = 4(а – 1)(а – 6).

Значить, повинна виконуватись нерівність 4(а – 1)(а – 6) > 0.

Маємо систему нерівностей:

Система нерівностей має розв’язок: 6

При яких значеннях параметра а нерівність 2х 2 + 4х + а

Якщо D 2 + 4х + а лежить у верхній півплощині; при будь-яких значеннях х значення функції у > 0.

Відповідь: при а > 2.

При яких значеннях параметра а система рівнянь

Графік першого рівняння – прямий кут, бісектриса якого належить осі ординат з вершиною в точці (0;2). Графік другого – коло радіуса 1 з центром в точці (0;а). Три точки перетину можливі лише у випадку, зображеному на малюнку; тобто при а = 3.

Відповідь: при а = 3.

Скільки розв’язків залежно від значення параметра а має рівняння

Побудуємо графік функції

Корені рівняння – абсциси точок перетину графіка даної функції з горизонтальними прямими у = а.

Тому при а > 8 – два розв’язки;

при а = 8 – безліч розв’язків;

при а – немає розв’язків.

Розв’яжіть рівняння для кожного значення параметра а:

Розкладемо на множники вирази:

Завдання для самостійного опрацювання.

1.При яких значеннях параметра а рівняння має два дійсні корені:

х 2 – 4ах + 3а + 1 = 0 А) 0,25 Б) – 0,25 1 Г) а 1

2.При яких значеннях параметра а рівняння не має коренів: х 2 + (а + 2) х + 4 = 0. А) 2 6 Г) а 2

3.При яких значеннях параметра а рівняння має два рівні корені: х 2 – ах + 4 = 0. А) а = 4 Б) а = – 4 В) а = 16 Г) а = – 4; а = 4

4.Знайдіть, при яких значеннях параметра а виконується нерівність при всіх дійсних значеннях х: ах 2 – 4х + а + 3 > 1 Б) а > 4 В) а > – 4 Г) а

5.При яких значеннях параметра а корені рівняння х 2 – (2а + 1) х + а 2 – 4а + 3 = 0 є додатними числами? А) а > – Б) а 3 Г) ≤ а 3

6.При яких значеннях параметра а не має розв’язків нерівність: ах 2 + 5ах + 4а + 3 Б) а > 0 В) а

7. Для кожного значення параметра а > 3 розв’яжіть нерівність:

9. При яких значеннях параметра а система рівнянь

А) а = 4 Б) а = 1 В) а = – 2 Г) а = – 4

А) а = – 1 Б) а = 1 В) а = 3 Г) а = – 3

Источник

Рівняння з параметрами це

Під час розв’язування рівнянь з параметрами потрібно враховувати те, що хід розв’язування та розв’язок залежать від значення параметра. Розв’язування рівнянь з параметрами вимагає ретельного аналізу та дослідження умов, оскільки потрібно логічно визначити всі можливі варіанти значення параметра, за яких рівняння мають розв’язок.

Розв’язати рівняння з параметром – це означає, що для кожного значення параметра слід встановити, чи має рівняння розв’язки; якщо так, то знайти ці розв’язки, які зазвичай залежать від параметра.

Слід пам’ятати, що універсальних методів розв’язування задач із параметрами немає. Найчастіше користуються алгебраїчними і геометричними (графічними) методами.

Існує певний алгоритм розв’язування рівнянь з параметрами.

Алгоритм розв’язування рівнянь з параметрами

1. Встановити область допустимих значень (ОДЗ) змінної та ОДЗ параметрів.

2. Виразити змінну через параметри.

3. Для кожного допустимого значення параметра знайти множину значень рівняння (розв’язків даної нерівності).

4. Дослідити особливі значення параметра, при яких корені рівняння існують, але не виражаються формулами,які дістали.

До найпростіших рівнянь з параметрами відносяться лінійні рівняння з параметрами. Розглянемо деякі приклади розв’язування рівнянь з параметрами.

№ 3. Розв’язати рівняння: ах + 5 = х + 5а.

Перенесемо доданки з х в ліву частину: ах – х = 5а-5

Винесемо х за дужки: х(а – 1) = 5а– 5

№ 4. Розв’язати рівняння: ax – 3 x = – 9.

Розглянемо усі можливі значення х в залежності від значень параметра:

Источник

Рішення рівнянь із параметрами

Рішення рівнянь із параметрами, зв’язаних із властивостями показовою, логарифмічною й тригонометричною функціями

Актуальність даної теми визначається необхідністю вміти вирішувати такі рівняння з параметрами при складанні незалежного оцінювання знань.

Ціль даної роботи розповісти про рішення рівнянь із параметрами, зв’язаних із властивостями показовою, логарифмічною й тригонометричною функціями.

Для досягнення поставленої мети необхідно вирішити наступні задачі:

дати визначення поняттям рівняння з параметрами;

показати принцип рішення даних рівнянь на загальних випадках;

показати рішення рівнянь із параметрами, зв’язаних із властивостями показовою, логарифмічною й тригонометричною функціями.

Для виконання поставленої мети були використані наступні методи: використання літератури різного типу, робота в групах на уроках алгебри й заняттях елективного курсу по математиці, участь проектної групи в міській конференції по даній темі в 2008 році.

Об’єктом дослідницької роботи було рішення рівнянь із параметрами, зв’язаних із властивостями вище представлених функцій.

Структура даної роботи містить у собі теорію, практичну частину, висновок, бібліографічний список.

Рішення рівнянь із параметрами

рівняння параметр функція логарифмічна

Задачі з параметрами відіграють важливу роль у формуванні логічного мислення й математичної культури в школярів, але їхнє рішення викликає в них значні утруднення. Це пов’язане з тим, що кожне рівняння з параметрами являє собою цілий клас звичайних рівнянь, для кожного з яких повинне бути отримане рішення. Такі задачі пропонуються на єдиному державному іспиті й на вступних іспитах у вузи.

Якщо в рівнянні деякі коефіцієнти задані не конкретними числовими значеннями, а позначені буквами, то вони називаються параметрами, а рівняння параметричним.

Необхідність акуратного обігу з параметром добре видна на тих прикладах, де заміна параметра числом робить задачу банальної. До таких задач, наприклад, ставляться: зрівняти два числа, вирішити лінійне або квадратне рівняння, нерівність і т.д.

Звичайно в рівняння буквами позначають невідомі.

знайти множину значень невідомому, задовольняючому цьому рівнянню. Іноді рівняння, крім букв, що позначають невідоме (X, Y,Z), містять інші букви, називані параметрами(a, b, c). Тоді ми маємо справу не з одним, а з нескінченною множиною рівнянь.

При рішенні таких рівнянь треба:

1) знайти множину всіх доступних значень параметрів;

2) перенести всі члени, що містять невідоме, у ліву частину рівняння, а всі члени, що не містять невідомого в праву;

3) привести подібні доданки;

4) вирішувати рівняння ax = b.

Можливо три випадки.

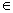
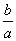
1. а 0, b – будь-яке дійсне число. Рівняння має єдине рішення х = .

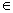
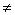
2. а = 0, b = 0. Рівняння приймає вид: 0х = 0, рішеннями є всі х R.

3. а = 0, b 0. Рівняння 0х = b

У тільки що розібраному прикладі запис відповіді практично повторює рішення. Проте, я вважаю за доцільне привести відповідь.

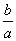
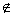
х = при а 0, b – будь-яке дійсне число;

Рішення рівнянь із параметрами, зв’язаних із властивостями показовою, тригонометричною й логарифмічною функціями

1. Знайдемо значення параметра n, при яких рівняння 15·10 х – 20 = n – n · 10 х + 1 не має коренів?

Рішення: перетворимо задане рівняння: 15·10 х – 20 = n – n · 10 х + 1 ; 15·10 х + n· 10 х + 1 = n + 20; 10 х ·(15 + 10n) = n + 20; 10 х = .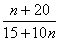

Рівняння не буде мати рішень при 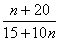≤ 0, оскільки 10 х завжди позитивно.

Відповідь: .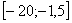

2. Знайдемо всі значення параметра а, при яких рівняння lg 2 (1 + х 2 ) + (3а – 2)· lg(1 + х 2 ) + а 2 = 0 не має рішень.

Источник

Роз`язування рівнянь і нерівностей з параметрами

Роз ` язування рівнянь і нерівностей з параметрами

Треба математику не т і льки викладати,

як науку абстрактну, а й переходити до

різноманітних практичных ії застосувань.

Тема уроку: Роз ` язування рівнянь з параметрами.(10клас).

Мета уроку: вивчити означення рівняння з параметрами,

навчитися розв ` язувати лінійні та дробові

рівняння з параметрами,

розвивати логічне мислення учнів, вміння

аналізувати, робити висновки,

4.) соціальні :-стимулювання пізнавальної активності учнів,

встановлення причинно-наслідкових зв ` язків.

1. Вступне слово вчителя.

Задачі з параметрами завжди зустрічалися на вступних іспитах до вищих навчальних закладів, і вже на протязі трьох років проведення тестування випускників середніх шкіл пропонуються при виконанні завдань високого рівня. Розв ` язання задач з параметрами є одним із самих ефективних способів розвинення інтелектуальних здібностей учнів. Взагалі, при розв ` язанні задач з хімії та фізики вам неодноразово приходилось розв ` зувати задачі з параметрами.

Які рівняння можна вважати рівняннями з параметрами?

Які рівняння з параметрами ви вже роз ` язували?

2.Актуалізація опорних знань учнів:

Розв`язування рівняння зручно записати у вигляді

Повторити загальний вигляд слідуючих функцій:

3. Вивчення нового матеріалу.

Рівнянням зі змінною х і параметром а називається рівняння

Розв ` язати рівняння з параметром — означає знайти для кожного допустимого значення а множину розв ` зків рівняння.

Для розв`язування рівнянь з параметрами необхідно знати властивості елементарних функцій, властивості рівнянь і нерівностей і вміти їх досліджувати. Одним із важливих етапів розв`язування рівнянь з параметрами є запис відповіді.

Розв`язувати рівняння з параметром доцільніше з а слідую чим планом.

План роз` язування рівнянь з параметрами .

1.Знайти критичні значення параметра.

2.Знайти розв`язкі рівняння для критичних значень параметра.

3.Знайти множини розв`язків на інтервалах між критичними значеннями параметра.

4.Побудувати графічну ілюстрацію і записати відповідь.

4.Сприймання і усвідомлення прийомів розв`язування

рівнянь з параметрами.

Колективне розв ` язування вправ.

Щоб знайти критичні значення параметра, необхідно знайти ті значення параметра, які обертають в нуль коефіцієнт при х.

Відповідь. Якщо , то розв ` язків немає;

якщо

Р` язування лінійних рівнянь з параметрами.

На початку уроку ми розглянули таблицю , в якій було показано, які можливі критичні значення лінійних рівнянь з параметрами.

За допомогою цієї схеми розв’яжіть рівняння з параметром.

Приклад 1 .

3 )Якщо , то рівняння можливо перетворити до виду х= 1/2 а.

1.Для кожного допустимого значення а розв’язати рівняння :

а) ( а -9)х= а +3;

б) ( а +1)х = а -1.

б) Для яких значень k рівняння

Питання вчителя : 1. Чи правильним шляхом пішли учні

3. Для яких значень k рівняння

( k =0, єдиний розв’язок); ( k =5,немає розв’язків )

6. Сприймання і усвідомлення методів розв’язування дро

бових рівнянь з параметрами.

— що називається множиною допустимих значень дробового

Колективне розв’язування вправ.

У даному рівнянні допустимими є будь-які значення параметра

якщо

Самостійно побудуйте графічну ілюстрацію.

Відповідь: якщо а = 8/9 або

то рівняння коренів немає.

якщо

При яких значеннях параметра а рівняння

має недодатні розв’язки? Знайти ці розв’язки.

якщо

7.Осмислення вивченого матеріалу.

а)Для яких значень t рівняння має додатні розв’язки?

б)Для яких значень k рівняння

в) Розв’язати рівняння :

; .

8.Підведення підсумків уроку.

Проаналізуйте приклади, які ми розв’язували на уроці.

1. Розв ` язати рівняння:

а) ;

б)

2. Знайти всі цілі корені рівнянь а) ах=а+5 ; б)

Тема уроку: Розв’язування квадратних рівнянь з параметрами.

Мета уроку: формувати уміння розв’язувати рівняння з двома па-

раметрами та квадратні рівняння з параметрами;

розвивати вміння аналізувати, робити висновки, зна-

ходити власні оригінальні способи розв’язків задачі;

виховувати інтерес до навчання, творче мислення.

—продуктивної творчої діяльності — вміння побачити та сформувати проблему, знаходити нові рішення, діяти в нестандартних ситуаціях;

— інформаційні – розуміння та усвідомлення інформації, залучення власного досвіду;

—комунікативні – розвитку культури математичного мовлення,

надання аргументованих відповідей, створення проблемних ситуацій;

—соціальні – формування власної оцінки і самооцінки, стимулювання пізнавальної активності учнів.

На дошці записано слова Рене Декарта:

«І чим важче доведення, т им б і льше задоволення тому, хто це доведення знайде.»

1. Перевірка домашнього завдання.

4 учня біля дошки обґрунтовують свої розв’язки.

2.Актуалізація опорних знань учнів.

Які рівняння називаються рівняннями з параметрами?

Як розв’язувати лінійні рівняння з параметрами?

Чим відрізняються розв’язання дробових рівнянь з параметрами від лінійних рівнянь з параметрами?

Як записувати відповідь при розв’язанні цих рівнянь?

3. Сприймання і усвідомлення особливостей розв’язування рівнянь з двома невідомими.

Учні обговорюють відповідь.

Скільки параметрів має це рівняння?

У якому вигляді можливо надати означення такого рівняння?

Заслуховуються і рецензуються відповіді учнів.

Вчитель.

1) називають недопустимою системою значень параметрів, якщо вираз f (х, y , a . b )=0 немає змісту ні для яких значень х і у;

2) називають допустимою системою значень параметрів, якщо вираз f (х, y , a . b )=0 має зміст для деяких значень х і у.

Група С виконує вправу

Після цього кожна з груп пропонує свої розв`язки біля дошки і обґрунтовує їх.

Рецензують їх розв’язки експерти з інших груп.

-дайте означення квадратного рівняння;

— за яких умов квадратне рівняння має два корені, один корінь, не має дійсних коренів;

— сформулюйте теорему Вієта;

Підвожу учнів до формулювання алгоритму розв’язування квадратних рівнянь з параметрами.

— якщо а= 0, то отримуємо лінійне рівняння;

— якщо то кількість коренів залежить від знака дискримінанта

якщо

Відповідь: якщо то розв’язків немає;

якщо

— Які особливості розв’язування квадратних рівнянь з параметрами?

1. Скласти лінійне рівняння з двома параметрами.

3. Розв’язати рівняння:

Тема уроку: Графічні методи розв’язування задач з

Мета уроку: формувати уміння розв’язувати задачі з параметрами,

розвивати уяву, творче мислення, вміння аналізувати,

тренувати зорову пам’ять,

виховувати культуру графічних побудов.

Тип уроку — комбінований.

—продуктивної творчої діяльності –активізацію творчих здібностей учнів;

—інформаційні –використання додаткової інформації, вміння переробити інформацію для отримання розв`язку задач і ;

— соціальну – підвищеня соціального статусу обдарованих учнів, виконання завдань різного рівня, створення проблемних ситуацій.

Чотирьом групам учнів були запропоновані завдання повторити властивості і графики елементарних функций, геометричні перетворення графіків функций.

Учні доповідають біля дошки, використовуючи заготовлені заздалегіть плакати і приклади.

Група А –лінійна функція та ії перетворення.

2. Сприймання і усвідомлення графічних методів розв ` язування задач з параметрами.

Побудова графічної моделі в системі координат х 0 а.

1. Будуємо графічну модель задачі.

2. Використовуючи прямі а= const отримуємо потрібну інформацію (наприклад, кількість коренів рівняння залежно від значень параметра, властивості розв’язків рівняння).

Побудова графічної моделі в системі координат х 0 у.

Параметр а нерівноправний зі зміною х.

2. У системі координат х 0 у будуємо графік і сукупність графіків

3. Аналізуючи гафічну модель, отримуємо потрібну інформацію.

Приклад. Визначте всі значення параметра а для яких рівняння

має хоч один додатній корінь.

Для кожного фіксованого значення параметра параметра а розв ` язками рівняння є абсцисами точок перетину даного графіка з горизонтальною прямою , яка відповідає цьому значенню параметра.